نیروی گرانشی چیست؟ – به زبان ساده
در این مطلب نیروی گرانشی را معرفی میکنیم و ویژگیها و تاثیرات آن را مورد بررسی قرار میدهیم. همچنین تفاوت مفهوم گرانش در فیزیک نیوتنی و نسبیت را بیان کرده و به بررسی نیروی پتانسیل گرانشی نیز خواهیم پرداخت. اگر مفهوم گرانش و نیروی گرانشی برای شما مبهم و گنگ است، خواندن این مطلب را به شما پیشنهاد میکنیم.


تاریخچه نیروی گرانشی در دنیای باستان
ارشمیدس فیلسوف یونان باستان مرکز ثقل یک مثلث را کشف کرد. وی همچنین عنوان کرد که اگر دو جرم برابر مرکز ثقل یکسانی نداشته باشند مرکز ثقل آن دو با هم در وسط خطی قرار میگیرد مرکز ثقل هر یک از جرم ها را به هم پیوند میدهد.
معمار و مهندس رومی Vitruvius in De Architectura فرض کرد که جاذبه یک جسم به وزن آن بستگی ندارد بلکه به ماهیت جسم بستگی دارد.
در هند باستان، آریاباتا ابتدا نیرویی را شناسایی کرد که توضیح دهد چرا با چرخش زمین اجسام به بیرون پرتاب نمیشوند. Brahmagupta گرانش را نیرویی جاذبه توصیف کرد و از اصطلاح gurutvaakarshan برای گرانش استفاده کرد.
تاریخچه نیروی گرانشی و انقلاب علمی
کارهای مدرن نظریه نیروی گرانشی با کار گالیله در اواخر قرن 16 و اوایل قرن 17 آغاز شد. گالیله در آزمایش معروف خود که انداختن توپها از برج پیزا و سپس اندازهگیری دقیق توپهایی که به سمت پایین سطح شیبدار حرکت میکردند نشان داد که شتاب نیروی گرانشی برای همه اجسام یکسان است.
این نظریه یک عقب گرد بزرگ از اعتقاد ارسطو بود. ارسطو معتقد بود که اجسام سنگینتر از شتاب نیروی گرانشی بالاتری برخوردارند. گالیله دلیل اصلی سقوط اجسام با جرم کمتر در جو را مقاومت هوا میدانست. بدین ترتیب کارهای گالیله زمینه را برای تدوین نظریه جاذبه نیوتن فراهم کرد.
نظریه جاذبه نیوتن و نیروی گرانشی

در سال 1687 ریاضیدان انگلیسی سر آیزاک نیوتون کتاب Principia را منتشر کرد که نظریه مجذور معکوس را برای نیروی گرانشی بیان کرد. به گفته نیوتن: «من نتیجه گرفتم که مقدار نیروهایی که سیارات را در مدار خود نگه میدارند باید متناسب با عکس مربع فاصله آنها از مراکزی باشند که در آن چرخیدهاند». بدین منظور او نیروی لازم برای نگه داشتن ماه در مدار خود را محاسبه کرد و آن را با نیروی جاذبه در سطح زمین مقایسه کرد و متوجه شد که تقریباً پاسخ یکسانی دارند. معادله نیوتن به شرح زیر بود:
که F نیرو، و جرم اجسام، r فاصله بین مراکز جرمها و G ثابت نیروی گرانشی است. نظریه نیوتن هنگامی که از آن برای پیش بینی وجود نپتون بر اساس حرکات اورانوس استفاده شد که امکان اثبات وجود آن با عملکرد سیارات دیگر وجود نداشت، از بزرگترین موفقیت خود برخوردار شد.
در حقیقت محاسبات «جان كوچ آدامز» (John Couch Adams) و «اوربن لو ویری» (Urbain Le Verrier) موقعیت كلی كره زمین را پیش بینی كرد و محاسبات لو ویری باعث شد كه «یوهان گوتفرید گال» (Johann Gottfried Galle) سیاره نپتون را کشف کند.
مغایرت در مدار عطارد، معایب نظریه نیوتن را نشان داد. در پایان قرن نوزدهم مشخص شد که مدار این سیاره اختلالاتی جزئی را نشان میدهد که نمیتوان آنها را کاملاً تحت نظریه نیوتن حساب کرد اما همه جستجوها برای یافتن جرم دیگری (مانند سیارهای که حتی نزدیکتر از عطارد به دور خورشید میچرخد) بی حاصل ماند. در نهایت این مسئله در سال 1915 با نظریه جدید آلبرت اینشتین یعنی نسبیت عام و محاسبه اختلال اندک مدار عطارد حل شد. این اختلاف پیشروی در حضیض (نقطهای از مدار یک سیاره، سیارک یا دنباله دار که در آن نقطه نزدیکترین فاصله به خورشید را دارد) عطارد به مقدار آرکثانیه در قرن بود.
گرچه نظریه نیوتن توسط نسبیت عام آلبرت انیشتین جایگزین شده است اما هنوز بیشتر محاسبات نیروی گرانشی غیر-نسبیتی مدرن با استفاده از نظریه نیوتن انجام میشود زیرا کار با آن سادهتر است و برای اکثر کاربردهایی که شامل جرمها، سرعتها و انرژیهای پایین هستند نتایج نسبتاً دقیقی ارائه میدهد.
اصل هم ارزی و نیروی گرانشی
اصل هم ارزی که توسط گروهی از دانشمندان و محققین در دورههای مختلف از جمله گالیله، «لوراند اِتوس» ( Loránd Eötvös) و اینشتین کشف شد بیانگر این ایده است که همه اجسام به یک شکل سقوط میکنند و تأثیرات نیروی گرانشی از برخی جنبههای افزایش و کاهش شتاب قابل تشخیص نیست. سادهترین راه برای آزمایش اصل هم ارزی ضعیف این است که دو جسم با جرمها یا ترکیبات مختلف را در خلا رها کنیم و ببینیم آیا همزمان به زمین برخورد میکنند یا خیر.
چنین آزمایشاتی نشان میدهد که وقتی سایر نیروها (مانند مقاومت هوا و اثرات الکترومغناطیسی) ناچیز هستند همه اجسام با سرعت یکسان سقوط میکنند. در تستهای پیچیدهتر از ترازوی پیچشی از نوعی که Eötvös ابداع کرده است استفاده میشود. آزمایشهای ماهوارهای به عنوان مثال STEP نیز برای آزمایشهای دقیقتر در فضا برنامه ریزی شده است.
انواع اصل همارزی را میتوان به سه دسته زیر تقسیمبندی کرد:
- اصل هم ارزی ضعیف: مسیر حرکت جرم نقطهای در یک میدان گرانشی فقط به موقعیت و سرعت اولیه آن بستگی دارد و از ترکیبات آن مستقل است.
- اصل هم ارزی اینشتین: نتیجه هر آزمایش محلی غیر گرانشی در یک آزمایشگاه که آزادانه در حال سقوط است، مستقل از سرعت آزمایشگاه و مکان آن در فضا-زمان است.
- اصل همارزی قوی که به هر دو مورد بالا نیاز دارد.
نسبیت عام و نیروی گرانشی

در نسبیت عام اثرات گرانش به جای نیرو به انحنای فضا-زمان نسبت داده میشود. نقطه آغازین نسبیت عام اصل همارزی است که سقوط آزاد را با حرکت لخت یکسان میداند و اجرام لخت را که در حال سقوط آزاد هستند نسبت به ناظران غیر لخت روی زمین در حال شتاب گرفتن در نظر میگیرد. اما در فیزیک نیوتون چنین شتابی نمیتواند اتفاق بیفتد مگر اینکه حداقل یکی از اجسام توسط یک نیرو مورد استفاده قرار گیرد.
نظریه اینشتین این بود که فضا-زمان توسط ماده خمیده میشود و اشیائی که به صورت آزاد در حال سقوط هستند در طول مسیرهای محلی مستقیم در فضا-زمان منحنی حرکت میکنند. این مسیرهای مستقیم را ژئودزیک مینامند. نظریه انیشتین مانند اولین قانون حرکت نیوتن میگوید اگر نیرویی بر جسمی وارد شود، جسم از مسیر ژئودزیک خود منحرف میشود.
به عنوان مثال زمانی که ایستادهایم روی یک ژئودزیک نیستیم زیرا مقاومت مکانیکی زمین به ما نیرویی به سمت بالا وارد میکند و در نتیجه ما غیر لخت هستیم. این موضوع توضیح میدهد که چرا حرکت در امتداد ژئودزیک در فضا-زمان لخت در نظر گرفته میشود.
اینشتین معادلات میدانی نسبیت عام را کشف کرد که مربوط به وجود ماده و انحنای فضا-زمان است و این معادلات به نام وی نامگذاری شدهاند. معادلات میدانی اینشتین مجموعهای از 10 معادله دیفرانسیل، همزمان و غیر خطی است. راه حلهای معادلات میدانی اینشتین اجزای تانسور متریک فضا-زمان هستند. یک متریک تانسوری هندسه فضا-زمان را توصیف میکند. مسیرهای ژئودزیکی برای یک فضا-زمان نیز از تانسور متریکی محاسبه میشود.
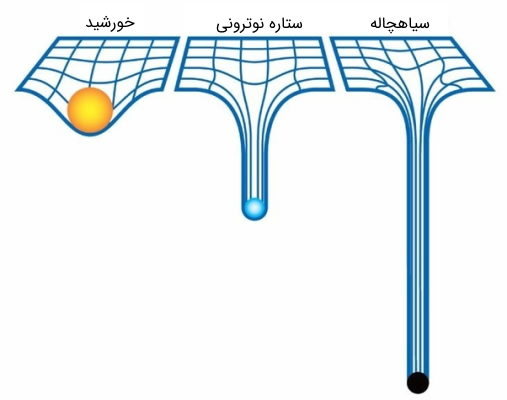
حل معادلات میدانی اینشتین
راه حلهای برجسته و مشهور معادلات میدانی اینشتین عبارتند از:
- جواب «شوارتزشیلد» (Schwarzschild solution) که فضا-زمان اطراف یک جرم عظیم بدون چرخش متقارن کروی را توصیف میکند. این حل برای اشیا بسیار کوچک و فشرده، یک سیاهچاله با تکینگی مرکزی ارائه میدهد. برای فاصله شعاعی از مرکز که بسیار بیشتر از شعاع شوارتزشیلد است شتابهای پیشبینی شده توسط جواب شوارتزشیلد عملاً مشابه پیشبینیهای نظریه نیروی گرانشی نیوتن است.
- جواب «رایسنر-نوردسترام» (Reissner-Nordström solution)، که در آن جسم مرکزی دارای بار الکتریکی است. برای بارهای با طول هندسی که کمتر از طول هندسی جرم جسم هستند، این حل سیاهچالههایی با افق رویداد دو برابر ایجاد میکند.
- جواب «کر» (Kerr solution) برای چرخش اجسام عظیم است. این راه حل همچنین سیاهچالههایی با چندین افق رویداد تولید میکند.
- راه حل «کر-نیومن» (Kerr-Newman solution) برای اجسام عظیم باردار و چرخان استفاده میشود. این راه حل همچنین سیاهچالههایی با چندین افق رویداد تولید میکند.
- جواب کیهان شناختی «فریدمن-لمیتر-رابرتسون-واکر» (Friedmann-Lemaître-Robertson-Walker solution) که انبساط جهان را پیش بینی میکند.
آزمونهای نظریه نسبیت عام
آزمونهای نسبیت عام شامل موارد زیر بودند:
- نسبیت عام توانست اختلال حضیض سیاره عطارد را محاسبه کند.
- پیش بینی اینکه زمان در پتانسیلهای پایینتر کندتر میشود (اتساع زمان گرانشی) توسط آزمایش «پوند-ربکا» (Pound–Rebka) در سال 1959، آزمایش «هافله-کیتینگ» (Hafele–Keating) و GPS تأیید شده است.
- پیش بینی انحراف نور اولین بار توسط «آرتور استنلی ادینگتون» (Arthur Stanley Eddington) از مشاهدات خود در هنگام خورشید گرفتگی 29 می 1919 تأیید شد. ادینگتون مطابق با پیش بینیهای نسبیت عام انحراف نور ستاره را دو برابر اندازه گیری شده توسط نظریه ذرهای نیوتن اندازه گیری کرد. اما با گذر زمان تفسیر وی از نتایج مورد اختلاف قرار گرفت.
- آزمایشات جدیدتر با استفاده از اندازه گیری تداخل رادیویی کوازارهایی که از پشت خورشید عبور میکنند با انحراف دقیقتر و منظمتر، انحراف نور به میزان پیش بینی شده توسط نسبیت عام را تأیید میکنند.
- تاخیر زمانی عبور نور از نزدیک یک جسم عظیم اولین بار توسط «اروین شاپیرو» (Irwin I. Shapiro) در سال 1964 در سیگنالهای فضاپیمای بین سیارهای شناسایی شد.
- تابش گرانشی به طور غیر مستقیم از طریق مطالعات تپ اخترهای دودویی تأیید شده است. در 11 فوریه 2016 همکاری بین دو پروژه LIGO و Virgo اولین مشاهده امواج گرانشی را اعلام کردند.
- «الكساندر فریدمن» (Alexander Friedmann) در سال 1922 دریافت كه معادلات اینشتین راه حلهای غیر ثابت (حتی در حضور ثابت كیهان شناسی) دارند. در سال 1927 «ژرژ لمیتر» (Georges Lemaître) نشان داد که راه حلهای ساکن معادلات اینشتین که در صورت ثابت بودن ثابت کیهانشناسی امکان پذیر است ناپایدار هستند و بنابراین جهان استاتیک متصور شده توسط اینشتین نمیتواند وجود داشته باشد. برای آشنایی بیشتر با مدل فریدمن-رابرتسون-واکر این مطلب را بخوانید.
- بعداً در سال 1931 اینشتین خود با نتایج فریدمن و لمیتر موافقت کرد. بنابراین نسبیت عام پیش بینی کرد که جهان باید غیر ایستا باشد یعنی باید منبسط یا منقبض شود. انبساط عالم که ادوین هابل در سال 1929 کشف کرد این پیش بینی را تأیید کرد. برای آشنایی بیشتر با محاسبات و پیشبینیهای هابل مطلب قانون هابل و ثابت هابل — به زبان ساده را مطالعه کنید.
- پیش بینی نظریه نسبیت عام از اعوجاج فضا-زمان به دلیل حضور یک جسم در چارچوب فضا-زمان با نتایج اخیر Gravity Probe B (یک ماهواره که ماموریت داشت تا دو پیشبینی نسبیت عام یعنی اعوجاج فضا-زمان و اثرات ژئودزیک را مورد آزمایش قرار دهد) مطابقت داشته است.
- نسبیت عام پیش بینی میکند که نور هنگام دور شدن از اجسام عظیم از طریق انتقال قرمز گرانشی، باید انرژی خود را از دست بدهد. این مورد در زمین و در منظومه شمسی در حدود سال 1960 تأیید شد.
نیروی گرانشی و مکانیک کوانتوم
یک سوال بی پاسخ این است که آیا میتوان فعل و انفعالات گرانش در مقیاس کوچک را با همان چارچوب مکانیک کوانتوم توصیف کرد؟ نسبیت عام خصوصیات اجسام بزرگ در مقیاس بزرگ را توصیف میکند در حالی که مکانیک کوانتوم چارچوبی برای توصیف فعل و انفعالات کوچکترین مقیاس ماده است. بدون اصلاح این چارچوبها ناسازگار هستند.
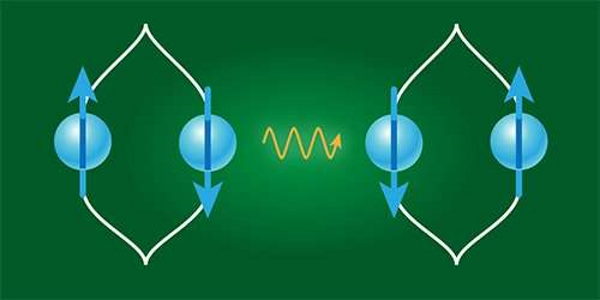
یک راه برای سازگار کردن این دو چارچوب توصیف گرانش در چارچوب تئوری میدان کوانتومی است که در توصیف دقیق سایر فعل و انفعالات اساسی موفق بوده است. همان طور که میدانید نیروی الکترومغناطیسی از تبادل فوتونهای مجازی ناشی میشود به همین ترتیب توصیف گرانش در نظریه میدانهای کوانتومی یا QFT این است که تبادل گراویتونهای مجازی وجود دارد.
این توصیف نسبیت عام را در محدوده تعاریف کلاسیک بازتولید میکند. با این حال، این توضیح در فواصل کوتاه در اندازه طول پلانک که تئوری کاملی از گرانش کوانتومی (یا یک رویکرد جدید به مکانیک کوانتومی) مورد نیاز است شکست میخورد.
نیروی گرانشی زمین چه قدر است؟
نیروی گرانشی یا جاذبه زمین برای ما بسیار مهم است زیرا بدون آن نمیتوانستیم روی زمین زندگی کنیم. جاذبه خورشید زمین را در مدار خود به دور خورشید نگه میدارد و ما را در یک فاصله ایمن از خود نگه میدارد تا از نور و گرمای خورشید لذت ببریم. دمای هوا و اتمسفر را برای تنفس پایین نگه میدارد. در حقیقت جاذبه همان چیزی است که دنیای ما را در کنار هم نگه میدارد.
با این حال نیروی گرانشی در همه جای زمین یکسان نیست. جاذبه زمین در مکانهایی که جرم کمتری دارند کمی قویتر است. ناسا از دو فضاپیما برای اندازه گیری این تغییرات در نیروی گرانشی زمین استفاده میکند. ماموریت این فضاپیماها بازیابی جاذبه و آزمایش آب و هوا یا به اختصار GRACE است.

GRACE تغییرات کوچک نیروی گرانشی را با گذشت زمان تشخیص میدهد. این تغییرات جزئیات مهمی در مورد سیاره ما نشان داده است. به عنوان مثال GRACE تغییرات سطح دریا را کنترل میکند و میتواند تغییراتی را در پوسته زمین که در اثر زلزله ایجاد شده است شناسایی کند.
نیروی گرانشی ماه چه قدر است؟
ماه تنها 17 درصد از نیروی گرانشی زمین را در اختیار دارد. با این حال نیروی گرانشی آن چند قرن است که از چرخیدن زمین به صورت وارونه یا تغییر قابل توجه آب و هوا جلوگیری کرده است. ماه نه تنها درخشانترین جسم در آسمان شب ما است بلکه یک هم تیمی برای زمین است که از آن مراقبت میکند.
گرانش ماه بیشتر به دلیل امواج جزر و مد در زمین شناخته میشود. با این وجود نقشهای مهم دیگری وجود دارد که نیروی گرانشی ماه بر روی زمین انجام میدهد.

جزر و مد قمری
جزر و مد به دلیل نیروی گرانشی ماه اتفاق میافتد. مکانهای مختلف روی زمین با ماه فاصلههای متفاوتی دارند، سمت نزدیک زمین حدود 59 برابر شعاع زمین و سمت دور زمین 61 برابر شعاع زمین از ماه فاصله دارد. در نتیجه وقتی ماه مستقیماً بر فراز مکانی روی زمین قرار دارد نیروی جاذبه آن قویتر است و بنابراین جزر و مد در آن ناحیه ایجاد میشود.
جالب است که همین اتفاق در سمت دور ماه نیز اتفاق میافتد در حالی که حتی گرانش ماه نمیتواند آب را به سمت مخالف مرکز زمین بکشد، در واقع همان کشش زمین است که منجر به جزر و مدهای بلند در این نواحی میشود. تفاوت مقدار نیروی جاذبه ماه بین دو طرف نزدیک و دور زمین حدود نیروی متوسط است.
جزر و مد نه تنها از گرانش ماه بلکه از مدار بیضوی آن نیز تأثیر میگیرد که نشان میدهد فاصله ماه از زمین تغییر میکند. همچنین خورشید نیز جزر و مد را تحت تأثیر قرار میدهد.
جزر و مد خورشیدی
جزر و مد در نقاط نزدیک و دور از خورشید نیز اتفاق میافتد. حتی اگر خورشید بسیار دورتر از ماه باشد اما گرانش آن به طور قابل توجهی قویتر است.
هم ترازی زمین، ماه و خورشید تعیین میکند که جزر و مد به چه اندازه است. اگر خورشید و ماه در یک خط با زمین قرار داشته باشند، گرانش آنها در یک جهت عمل میکند و بزرگترین جزر و مد را ایجاد میکند، جزر و مد بهاری. جزر و مد بهاری در طول ظهور رویداد «ماه» (moon) جدید یا ماه کامل رخ میدهد.
از طرف دیگر در طول ربع اول یا آخر سیاره ماه، خط زمین-ماه عمود بر خط خورشید-زمین است. بنابراین ، جزر و مد توسط ماه با اثرات خفیف از سمت خورشید کاهش یافته و جزر و مدهای ضعیفی ایجاد میشوند که به آنها اصطلاحاً جزر و مدهای بسیار ضعیف یا neap tides میگویند. همچنین عامل دیگری نیز وجود دارد که جزر و مد را تحت تأثیر قرار میدهد، این عامل خود اقیانوس است.
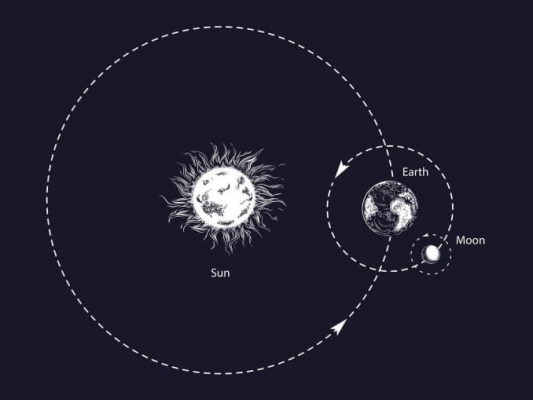
به غیر از خورشید و ماه، شکل کف اقیانوس در نزدیکی ساحل و جریانها و امواج در منطقه نیز بر ارتفاع جزر و مد در یک مکان خاص تأثیر میگذارد. خلیج فوندی بین نوا اسکوشیا و نیوبرانزویک در کانادا میزبان بالاترین جزر و مد در کره زمین است که اختلاف آن با جزر و مدهای کوچک میتواند بیش از 15 متر باشد. مواد جامد نیز در این اقیانوس همین نیرو را تجربه میکنند.
سرعت زمین و نیروی گرانشی ماه
نیروهای جزر و مدی روزها را بر روی زمین طولانیتر میکنند و سبب افزایش فاصله ماه از زمین میشوند. حدود 41/2 میلیارد سال پیش ماه شاید هفت برابر به زمین نزدیکتر بود و هر روز در کره زمین فقط چند ساعت طول میکشید زیرا خیلی سریعتر میچرخید.
زمین سریعتر از ماه میچرخد بنابراین وقتی ماه درست بالای یک مکان قرار دارد زمین تقریباً سریع از این حالت خارج میشود و تغییر مکان میدهد. با این وجود این تغییر مکان زمین مدتی طول میکشد و سبب جذر و مدهای بلند میشود و مجدداً زمانی طول میکشد تا شرایط به حالت عادی برگردد.
در حالی که برآمدگی جزر و مدی کمی از ماه جلوتر است گرانش ماه بر روی برآمدگی جزر و مدی سبب میشود تا کمی آن را به عقب کشیده و از این رو چرخش زمین را کند میکند. در حال حاضر نرخ کاهش سرعت چرخش زمین تنها دو ثانیه در هر 100,000 سال است.
مرجانهای دریایی شواهدی از کاهش سرعت زمین هستند. فسیل مرجانهای بیش از 400 میلیون سال پیش 420 روز در یک سال را نشان میدهند. در حالی که مرجانهای جوان روزهای کمتری در سال را نشان میدهند که به این معنی است که طول روزها بیشتر شده است.
پرسشهایی در مورد نیروی گرانشی در ماه
پرسش: آیا نیروی گرانشی روی ماه وجود دارد؟
پاسخ: نیروی جاذبه ماه بسیار کمتر از زمین است اما برای زمین بسیار مهم است. این نیرو باعث میشود زمین سریعتر نچرخد یا زاویه چرخش را به طور قابل توجهی تغییر ندهد، بنابراین شرایط را روی زمین ثابت نگه میدارد.
پرسش: گرانش ماه نسبت به زمین چقدر است؟
پاسخ: ماه دارای 17 درصد جاذبه زمین است اما نیروی گرانش آن به قدری قوی است که زمین را از تغییر شیب مداری به شدت باز دارد.
پرسش: نیروی جاذبه ماه چگونه روی زمین تأثیر میگذارد؟
پاسخ: نیروی جاذبه ماه نقش مهمی در جلوگیری از تغییر شیب مدار در زمین داشته است. بدون آن زمین میتوانست شیب چرخش مناسب را برای شرایط مناسب زندگی بر روی آن را از دست بدهد.
پرسش: بدون ماه چه اتفاقی میافتد؟
پاسخ: به زبان ساده، بدون ماه و نیروی جاذبه آن زندگی در کره زمین غیرممکن است. آبی که روی سطح زمین باقی میماند، آب و هوای پایدار و سرعت چرخشی پایدار سیاره زمین همه از نتایج نیروی گرانش ماه است.
ثابت جهانی نیروی گرانشی چیست؟
ثابت جاذبه یا ثابت جهانی گرانش به سه روش اندازهگیری شده است:
- مقایسه کشش در یک توده بزرگ طبیعی با زمین
- اندازه گیری با ایجاد تعادل آزمایشگاهی بر روی یک جسم تحت تاثیر نیروی جاذبه زمین
- اندازه گیری مستقیم نیرو بین دو جرم در آزمایشگاه
اولین روش توسط نیوتن پیشنهاد شد و اولین مشاهدات در سال 1774 توسط ستاره شناس انگلیسی «نویل ماسکلین» (Nevil Maskelyne) در کوه Schiehallion در اسکاتلند انجام شد.
روش تعادل آزمایشگاهی در اواخر دهه 1800 توسط «جان هنری پوینتینگ» (John Henry Poynting) فیزیکدان بریتانیایی، توسعه یافت و البته همه اندازهگیریهای اخیر ثابت گرانش شامل استفاده از ترازوی پیچشی به شکلهای متفاوت یا روشهای دیگر برای اندازهگیری مستقیم آزمایشگاهی نیرو بین دو جسم بوده است.
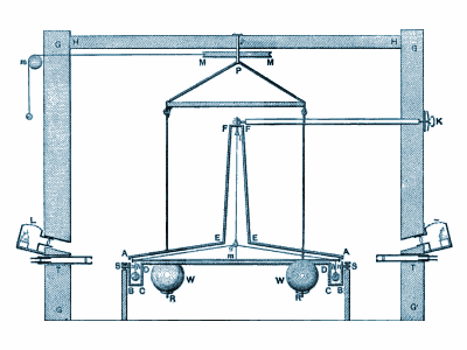
ترازوی پیچشی اولین بار توسط «میشل» (Michell) اختراع شده که قبل از استفاده از آن برای اندازهگیری G یا ثابت گرانش درگذشت. «کاوندیش» (Cavendish) از طراحی میشل استفاده کرد تا اولین اندازه گیری قابل اعتماد G را در سال 1798 انجام دهد.
اندازهگیری کاوندیش نسبتاً دقیق بود و فقط در آزمایشات و زمانهای اخیر است که نتایج به وضوح بهتری به دست آمده است. در این روش کاوندیش تغییر انحراف تعادل را هنگام جابجایی اجسام توسط جاذبه از یک طرف به طرف دیگر تیر پیچشی اندازهگیری کرد.
روش انحراف در اواخر دهه 1800 توسط «سر چارلز ورنون بویز» (Sir Charles Vernon Boys) فیزیکدان انگلیسی، که از سوسپانسیون یک فیبر ظریف از سیلیس ذوب شده برای آونگ استفاده کرد و آن را به بالاترین حد پیشرفت و توسعه خود رساند مورد تجزیه و تحلیل قرار گرفت. در یک نوع از این روش، انحراف تعادل توسط یک کنترل سروو ثابت حفظ و بررسی میشود.
روش دوم شامل تغییر در دوره نوسان ترازوی پیچشی در هنگام قرار گرفتن جرمهای تحت جاذبه نزدیک به آن است به گونهای که دوره نوسان در یک موقعیت کوتاه شده و در موقعیت دیگر طولانی میشود.
اندازهگیری دوره نوسان را میتوان دقیقتر از اندازهگیری انحراف انجام داد و روش معرفی شده توسط «کارل براون» (Carl Braun) از اتریش در سال 1897، در بسیاری از اندازهگیریهای دیگر نیز استفاده شده است.
در روش سوم برای اندازهگیری ثابت گرانش شتاب تودههای معلق زمانی که آنها به سمت تودههای بزرگ جذب میشوند اندازهگیری میشود.
در آرایش دیگری، تعادل با جرمهای سنگینی که تحت نیروی جاذبه به سمت یکدیگر کشیده میشوند در نزدیکی یک تعادل آزمایشی آزاد به گونهای تنظیم میشود که با دوره نوسان تراز آزمون در نوسان باشد.
سپس جرم دومی با دامنهای که اندازه ثابت گرانش است به سمت نوسانات تشدید هدایت میشود. این تکنیک برای اولین بار توسط J. Zahradnicek از چکسلواکی در طول دهه 1930 به کار گرفته شد و حدود 40 سال بعد توسط C. Pontikis از فرانسه مجدداً استفاده شد.
سوسپانسیونها برای تعادل دو بازو و برای مقایسه جرمها و توازنهای پیچشی به شدت توسط T.J. Quinn و همکارانش در دفتر بین المللی وزن و اندازهگیری در نزدیکی پاریس مورد استقبال و استفاده قرار گرفت و آنها دریافتند که سیستمهای سوسپانسیون با نوارهای نازک فلزی و نه سیم، پایدارترین سیستمها را فراهم میکند.
آنها از تعادل با چنین سوسپانسیونهایی برای جستجوی انحراف از پیش بینیهای نسبیت عام استفاده کردهاند و اخیراً از ترازوی پیچشی با استفاده از سوسپانسیون نواری در دو اندازهگیری جدید از ثابت گرانش بهره بردهاند.
بسیاری از اندازهگیریها برای تعیین ثابت گرانش یا G در پنج سال 1996 تا 2001 انجام شده و در جدول زیر به صورت خلاصه آورده شده است. با این حال علیرغم توجه زیادی که به اشتباهات سیستماتیک در این آزمایشات داده شده است از دامنه نتایج مشخص است که هنوز هم اختلافات جدی و بسیار بیشتری از اشتباهات تصادفی آشکار، در تعیین ثابت گرانش یا G وجود دارد.
در سال 2001 بهترین تخمین برای ثابت گرانش یا G اعلام شد. نتایج قبل از 1982، مقدار کمتری در حدود را نشان میدهد، اما نتایج مربوط به سال 1996 به بعد مقدار بزرگتری را نشان میدهد.
| مقادیر ثابت جهانی گرانش | ||
| انجام دهنده آزمایش | سال/ روش | مقدار () |
| «کاوندیش» (H. Cavendish) | 1798/ ترازوی پیچشی (انحراف) | |
| «پوینتینگ» (J.H. Poynting) | 1891/ تعادل معمولی | |
| «بویز» (C.V. Boys) | 1895/ ترازوی پیچشی (انحراف) | |
| «براون» (C. Braun) | 1897/ ترازوی پیچشی (انحراف) | |
| «براون» (C. Braun) | 1897/ ترازوی پیچشی (دوره حرکت) | |
| «هِیل» (P.R. Heyl) | 1930/ ترازوی پیچشی (دوره حرکت) | |
| «زاهرادنیک» (J. Zahradnicek ) | 1932/ ترازوی پیچشی (تشدید) | |
| «هِیل» (P.R. Heyl) و «کرزانوسکی» (P. Chrzanowski) | 1942/ ترازوی پیچشی (دوره حرکت) | |
| «پونتیکیس» (C. Pontikis) | 1972/ ترازوی پیچشی (تشدید) | |
| «لوتر» (G.G. Luther) و «تولر» (W.R. Towler) | 1982/ ترازوی پیچشی (دوره حرکت) | |
| «بوئر» (H. de Boer) | 1987/ جیوه شناور (انحراف) | |
| «میکالیس» (W. Michaelis) | 1996/ غوطهوری (انحراف) | |
| «باگلی» (C.H. Bagley) و «لوتر» (G.G. Luther) | 1997/ ترازوی پیچشی (دوره حرکت) | |
| «کارگویز» (O.V. Karagioz) | 1998/ ترازوی پیچشی (دوره حرکت) | |
| «لو» (J. Luo) | 1999/ ترازوی پیچشی (دوره حرکت) | |
| «فیتزگرالد» (M.P. Fitzgerald) و «آرمسترانگ» (T.R. Armstrong) | 1999/ ترازوی پیچشی (انحراف) | |
| «نولتینگ» (F. Nolting) | 1999/ انحراف عادی | |
| «کلِینوس» (U. Kleinvoss) | 1999/ انحراف آونگ | |
| «گوندلاخ» (J.H. Gundlach) و «مرکویتز» (S.M. Merkowitz) | 2000/ ترازوی پیچشی (شتاب) | |
| «کویین» (T.J. Quinn) | 2001/ ترازوی پیچشی (سروو) | |
| «کویین» (T.J. Quinn) | 2001/ ترازوی پیچشی (انحراف) | |
تغییر ثابت جاذبه یا ثابت نیروی گرانشی با زمان
فیزیکدان انگلیسی قرن بیستم «دیراک» (P.A.M. Dirac) در میان دیگر محققین اظهار داشت که مقدار ثابت گرانش ممکن است متناسب با سن جهان باشد. نرخهای دیگر تغییر ثابت گرانش در طول زمان نیز پیشنهاد شده است.
این تغییرات بسیار کوچک است و برابر با یک واحد در هر سال است. در این حالت اگر سن جهان سال در نظر گرفته شود با این نرخ تغییر ثابت گرانش در حال حاضر امکان آزمایش این فرضیه وجود ندارد.
با این وجود امکان جستجوی تأثیرات هرگونه تغییر ثابت گرانش در مدار یک جرم آسمانی به ویژه ماه وجود دارد. هر از گاهی ادعا می شود که ممکن است چنین اثراتی شناسایی شده باشد اما هنوز قطعیتی وجود ندارد.
ثابت بنیادی G یا ثابت جهانی نیروی گرانشی
ثابت جاذبه زمین به وضوح یک مقدار اساسی است زیرا به نظر میرسد ساختار مقیاس کل عالم را تعیین میکند. گرانش یک مقدار اساسی است خواه یک پارامتر هندسی باشد طبق نظریه نسبیت عام، یا قدرت یک میدان همان طور که در نظریه اتحاد نیروها بررسی میشود.
این واقعیت تا آنجا که مشخص است این است که گرانش به هیچ عامل فیزیکی دیگری بستگی ندارد و این موضوع این احتمال را ایجاد میکند که مقدار G نشان دهنده محدودیت اساسی در امکان اندازه گیری فیزیکی است. در حقیقت نسبیت خاص نتیجه این واقعیت است که در فواصلی کوتاهتر از کوتاهترین فاصله شناخته شده، اندازه گیری جداگانه از طول و زمان غیرممکن است.
تفاوت ثابت نیروی گرانشی (G) و شتاب گرانش (g) چیست؟
شتاب گرانش را با g و ثابت گرانش را با G نمایش میدهیم. در حقیقت شتاب روی یک جسم در اثر نیروی جاذبه هر جسم عظیم دیگری توسط g نشان داده میشود. همچنین نیروی جاذبه بین هر دو جسمی را که در فاصله واحد از یکدیگر قرار دارند ثابت گرانش جهانی مینامند که با G نشان داده میشود.
رابطه بین G و g متناسب نیست و این بدان معنا است که آنها موجودیت مستقلی دارند. در واقع بر اساس رابطه نیروی گرانش و قانون دوم نیوتون داریم:
انرژی پتانسیل گرانشی چیست؟
همه ما به طور غریزی می دانیم که وزنه سنگینی که بالای سر کسی بلند شده نشان دهنده یک وضعیت بالقوه خطرناک است. وزنه ممکن است کاملاً ایمن باشد بنابراین لزوماً خطرناک نیست. نگرانی ما این است که هر نیرویی که برای تأمین وزن در برابر گرانش در جریان است از کار بیفتد. برای استفاده از اصطلاحات صحیح فیزیک در حقیقت ما نگران انرژی پتانسیل گرانشی وزن هستیم.
تمام نیروهای پایستار دارای انرژی پتانسیل مرتبط با خود هستند. نیروی جاذبه نیروی گرانشی نیز از این قاعده مستثنی نیست، به انرژی پتانسیل گرانشی معمولاً نماد داده میشود. این نشان دهنده مقدار پتانسیلی است که یک جسم در نتیجه قرار گرفتن در یک موقعیت خاص در یک میدان گرانشی مجبور به انجام کار به اندازه آن است.
در نظر بگیرید که جسمی با جرم m در ارتفاع h در برابر نیروی جاذبه قرار گرفته است، همانطور که در زیر نشان داده شده است. جسم توسط قرقره و طناب به صورت عمودی بلند شده است و بنابراین نیروی ناشی از بلند کردن جعبه و نیروی ناشی از گرانش موازی هستند.
اگر g اندازه شتاب گرانشی باشد میتوان کار حاصل از نیروی وارد شده بر وزن را با ضرب اندازه نیروی جاذبه در ارتفاع پیدا کرد. همچنین فرض میکنیم که اندازه شتاب گرانش در طول ارتفاع h ثابت است و داریم:
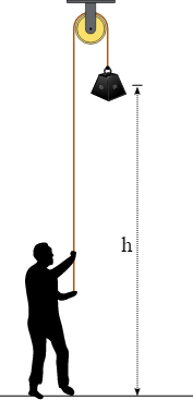
اگر نیرو برداشته شود جسم دوباره به زمین میافتد و انرژی پتانسیل گرانشی به انرژی جنبشی جسم در حال سقوط منتقل میشود. در مطلب پایستگی انرژی در مورد چگونگی تبدیل انرژی پتانسیل گرانشی به شکلهای دیگر انرژی صحبت کردهایم.
آنچه در مورد انرژی پتانسیل گرانشی جالب است این است که نقطه صفر انرژی به دلخواه انتخاب میشود. به عبارت دیگر ما آزاد هستیم که هر سطح عمودی را به عنوان مکانی که در آن است انتخاب کنیم.
برای مسائل مربوط به مکانیک یک نقطه صفر مناسب در کف آزمایشگاه یا در سطح یک جدول است. با این حال در اصل ما میتوانیم هر نقطه مرجعی را انتخاب کنیم که گاهی اوقات datum نامیده میشود.
در صورت عبور جسم از نقطه صفر انرژی پتانسیل گرانشی حتی میتواند منفی باشد و در حقیقت این پدیده مشکلی ایجاد نمیکند و فقط باید مطمئن باشیم که از همان نقطه صفر به طور مداوم در محاسبات استفاده میشود.
پرسش: اگر سیستم آسانسور دارای بازده کلی باشد، آسانسوری که یک فرد 75 کیلوگرمی را از ارتفاع 50 متر بلند میکند چه مقدار انرژی الکتریکی مصرف میکند؟ فرض کنید جرم کابین آسانسور خالی با یک وزنه تعادل به درستی متعادل شده باشد.
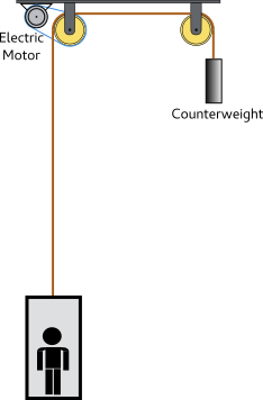
پاسخ: انرژی الکتریکی از شبکه به دلیل اصطکاک داخل سیستم آسانسور به انرژی پتانسیل گرانشی شخص و گرما منتقل میشود.از آنجا که واگن آسانسور دارای وزنه تعادل است در انرژی پتانسیل گرانشی سیستم وزنه تعادل آسانسور تغییری ایجاد نمیشود. با استفاده از معادله انرژی پتانسیل گرانشی ابتدا تغییر در انرژی پتانسیل گرانشی شخص یعنی را پیدا میکنیم:
به ما گفته شده است که این سیستم دارای کارایی کلی است. این بدان معنی است که از انرژی الکتریکی مورد استفاده موتور به کار مفید که در این حالت انرژی پتانسیل گرانشی است منتقل میشود و باقیمانده به عنوان انرژی اتلافی به محیط داده میشود. بنابراین کل انرژی الکتریکی مصرفی برابر است با:
پرسش: در مثال بالا هزینه برق با فرض اینکه قیمت آن $$10\ \frac{$}{kW.hr}$$
پاسخ: از تعریف توان میدانیم که انرژی کل برابر با حاصلضرب توان در مسافت است و داریم:
در نتیجه هزینه برق برابر با است و هزینه برق برای حرکت داده شده در مثال بالا برابر است با:
پرسش: انرژی پتانسیل گرانشی یکی از معدود اشکال انرژی است که میتواند برای ذخیره سازی عملی انرژی در مقیاس بسیار بزرگ مورد استفاده قرار گیرد. ذخیره انرژی در مقیاس بسیار بزرگ برای ذخیره انرژی الکتریکی اضافی از منابع انرژی باد و خورشید مورد نیاز است تا بتواند در زمان اوج تقاضا به شبکه برق منتقل شود. این را میتوان با سیستمهای برق آبی حلقههای پمپ شده به دست آورد. تصویر زیر نمونهای از چنین سیستمی را نشان میدهد. آب با استفاده از انرژی اضافی برای هدایت موتوری که پمپ توربین را حرکت میدهد به مخزن بالایی پمپ میشود.
وقتی تقاضای انرژی زیاد باشد جریان معکوس میشود و پمپ به ژنراتوری تبدیل میشود که توسط انرژی پتانسیل گرانشی آب را به مخزن فوقانی هدایت میکند. میتوان آب را خیلی سریع پمپاژ کرد تا اوج مصرف کل یک شهر یا حتی بسیاری از شهرها را تأمین کند.
ایستگاه حلقه پمپاژ Bath County بزرگترین سیستم برق آبی حلقههای پمپاژ در جهان است. این سرویس به 60 میلیون نفر خدمت میکند و ظرفیت تولید آن در حدود 3 گیگاوات است.
اختلاف ارتفاع این سیستم 380 متر است. فرض کنید این سیستم دارای راندمان کلی انرژی است. در مدت 30 دقیقه چه حجمی از آب مخزن فوقانی باید از توربین جریان یابد تا بتواند در این زمان میزان مصرف شهری که 3 گیگاوات است را تامین کند؟
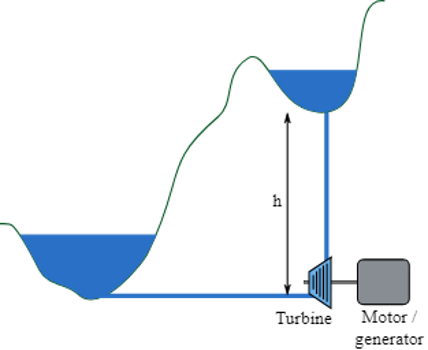
پاسخ: در ابتدا مقدار انرژی مورد نیاز را محاسبه میکنیم و این مقدار انرژی برابر با حاصلضرب توان در زمان است و داریم:
با توجه به اینکه راندمان این سیستم است ما انرژی پتانسیل بیشتری نسبت به این مقدار نیاز داریم. در حقیقت باید ضریب را در این مقدار انرژی ضرب کنیم تا انرژی پتانسیل گرانشی را به دست آوریم و داریم:
جرم آب مورد نیاز را میتوان از رابطه انرژی پتانسیل به دست آورد و داریم:
میدانیم یک لیتر آب جرمی برابر با یک کیلوگرم دارد. در نتیجه حجم آب مورد نیاز برابر با 1/81 مگالیتر است.
نیروی متوازن چیست؟
وقتی اندازه دو نیرو که بر روی یک جسم تأثیر میگذارند برابر باشند اما در جهت مخالف عمل کنند میگوییم آنها نیروهای متوازن هستند و جسم در تعادل است. اگر نیروهای وارد بر یک جسم متوازن باشند (یا اگر نیرویی روی جسم وارد نشود) حالتهای زیر اتفاق میافتد:
- یک شی در حالت ثابت، حالت ثابت خود را حفظ میکند.
- یک جسم در حال حرکت به همان سرعت و در همان جهت حرکت میکند.
به یاد داشته باشید که یک جسم میتواند در حال حرکت باشد حتی اگر هیچ نیرویی بر آن وارد نشود.
نمودار نیرو
با استفاده از نمودار نیرو میتوانیم نیروهای وارد بر یک جسم را نشان دهیم. در نمودار نیرو یک پیکان نمایانگر هر نیرو است. این پیکان نشان میدهد که
- اندازه نیرو چه قدر است (هرچه پیکان بلندتر باشد نیرو بیشتر است).
- جهتی که نیرو بر جسم اعمال میشود در کدام جهت است.
پیکان باید با نام نیرو و اندازه آن بر حسب نیوتن برچسب گذاری شود که در ادامه چند نمونه از شرایط مربوط به نیروهای متوازن آورده شده است.
اشیای آویزان
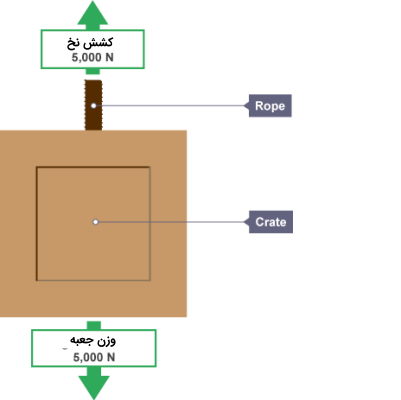
اندازه نیروهای موجود در این جعبه آویز برابر است اما در جهت مخالف عمل میکنند. نیروی وزن به سمت پایین و نیروی کشش طناب به سمت بالا بر جسم اعمال میشوند.
جسم شناور بر روی آب
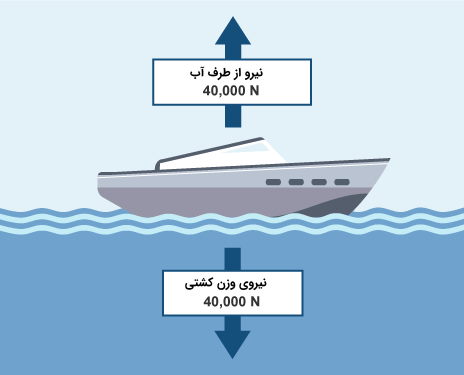
اجسام وقتی بر روی آب شناور میشوند که وزن آنها با نیرویی که از طرف آب بر آنها وارد میشود برابر باشند. همچنین زمانی که این دو نیرو با هم برابر نباشند جسم در آب فرو میرود و غرق میشود.
جسم ساکن بر روی سطح
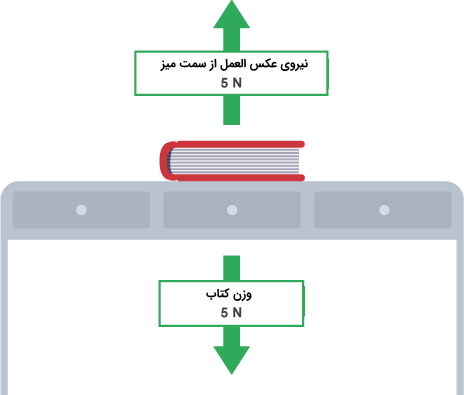
وقتی جسمی روی سطحی مانند میز یا زمین قرار میگیرد نیروی عکس العمل از زمین وزن آن را متوازن کرده و تعادل ایجاد میکند. زمین به طرف جسم به سمت بالا نیرو وارد میکند و نیروی عمل همان چیزی است که هنگام ایستادن در پاهای خود بر روی زمین احساس میکنید. بدون این نیروی متعادل کننده در زمین فرو میروید.
آیا گرانش نیروی تماسی است؟
خیر، گرانشی نیروی تماسی نیست. به این معنا که لزوماً در تماس دو جسم با یکدیگر این نیرو اعمال نمیشود. نیروی گرانشی یا جاذبه بر تمامی اجسام و در همه زمانها بر وی زمین اعمال میشود.
جمع بندی
در این مطلب نیروی گرانشی را مورد بحث و بررسی قرار دادیم. در ابتدای ای نوشتار نگاهی به تاریخچه نیروی گرانشی و تعاریف مختلف آن داشتیم. سپس و در ادامه نیروی گرانش زمین و ماه را بررسی کردیم و تفاوت شتاب گرانشی و ثابت جهانی نیروی گرانشی را بعد از معرفی و نحوه اندازهگیری ثابت جهانی گرانش مورد بحث قرار دادیم. در ادامه و در انتهای این مطلب نیروی پتانسیل گرانشی و نیروی متوازن را معرفی کردیم.













با عرض سلام و تشکر بابت زحمات شما.
معمولا می گویند که اثر نیروی گرانشی نیوتن با سرعت بینهایت پخش می شود، زیرا در فرمول جاذبه وی عنصر زمان یافت نمی شود. برای رفع این مشکل آیا نمی توان در مخرج کسر بجای R بتوان 2 از حاصلضرب ct بتوان 2 استفاده کرد و c بتوان 2 را از مخرج کسر جدا نمود و آنرا در ثابت جاذبه یعنی G ادغام نمود ؟ از این طریق یک فرمول نوین گرانش ایجاد خواهد گردید که بر اساس آن، انتشار اثر نیرو دیگر نمی تواند مستقل از گذر زمان باشد بلکه وابسته به مجذور زمان.
یک اشاره جنبی کوتاه که به ظاهر شاید ربطی به موضوع نداشته باشد: نام نیوتن به زبان انگلیسی بصورت Issac نوشته می شود که همسان نام فرزند دوم ابراهیم پیامبر قوم یهود می باشد و به زبان عربی تبدیل به اسحاق گردیده است. این نام از دو واژه فارسی ساخته شده است یکی Isa و دیگری ac . ایسا به زبان فارسی به معنای ” شبیه یا مثل این ” می باشد و پسوند اَک نشانه مصغر می باشد. لذا ایساّک به معنای ایسای کوچک است. پیشوایان دینی اقوام یهود و مسیحی و زرتشتی و مسلمان در طول تاریخ تاکنون به معنای نهفته در پشت این نام پی نبرده اند، زیرا به این آگاهی نرسیده اند که این نام به زبان فارسی می باشد. علامت تشدید را اگر از روی حرف الف برداریم آنگاه این نام به شکل زیر از هم تفکیک می شود : ایسا اک.
سلام و روز شما به خیر؛
تمام قوانینی که میخواهید به دنیای فیزیک اضافه کنید لازم است که از طریق آن قوانین پایستگی فیزیک برقرار باقی بماند. با این اوصاف میتوانید بررسی کنید که آیا فرمول نوین گرانش شما این قوانین را نقض میکند یا خیر و سپس در مورد معنای فیزیکی آن میتوان بحث کرد. در مورد سرعت پخش نیروی گرانشی نیز این نیرو با سرعت نور پخش میشود و بی نهایت نیست.
از همراهی شما به فرادرس خرسندیم.
سلام،
بین دو عبارت زیر چه تفاوت معنایی می تواند وجود داشته باشد :
الف – قبل از آغاز زمان .
ب – قبل از آغاز حرکت زمان.
به نظر این حقیر معنای عبارت اول این است که قبل از آغاز زمان، زمان وجود نداشته است و تنها پس از آغاز به وجود آمده است. معنای عبارت دوم این است که زمان قبل از آغاز حرکت وجود داشته اما ساکن و یا بدون حرکت بوده است. اگر منجمین و کیهان شناسان بتوانند بین معانی این دو عبارت تمیز قائل شوند، آنگاه یک قدم به سوی ادغام نسبیت عام و مکانیک کوانتایی یعنی فرمول بندی گرانش کوانتمی پیش روی کرده اند. به امید موفقیت بیشتر.
سلام، آیا با تغییر سرعت جسم جرم آن جسم هم تغییر میکند؟.در خیلی مقاله ها این طوری گفته شده؛اما آیا این جمله درست است؟
سلام و روز شما به خیر؛
این موضوع در سیستم کلاسیک که سرعت جسم بسیار کوچکتر از سرعت نور است در نظر گرفته نمیشود زیرا مقدار جرم کاهیده بسیار ناچیز است به نوعی که میتوان از آن صرف نظر کرد. در سرعتهای نزدیک به سرعت نور جرم کاهیده وجود دارد.
از اینکه با فرادرس همراه هستید خرسندیم.
سلام میتونیم بگیم که اگر به جسم ۱ کیلوگرمی به اندازه ۲۰ نیوتون نیرو وارد کنیم تندی اون میشه ۲۰متر بر ثانیه؟
سلام و روز شما به خیر؛
نیرو در فیزیک کلاسیک برابر با حاصلضرب جرم در شتاب است. در نتیجه اگر جرم شما یک کیلوگرم باشد، شتاب حرکت 20 متر بر مجذور ثانیه خواهد شد. برای آشنایی بیشتر مطلب قانون دوم نیوتن را در فرادرس مطالعه کنید.
از اینکه با فرادرس همراه هستید، خرسندیم.