نوسان در مدارهای الکتریکی — از صفر تا صد
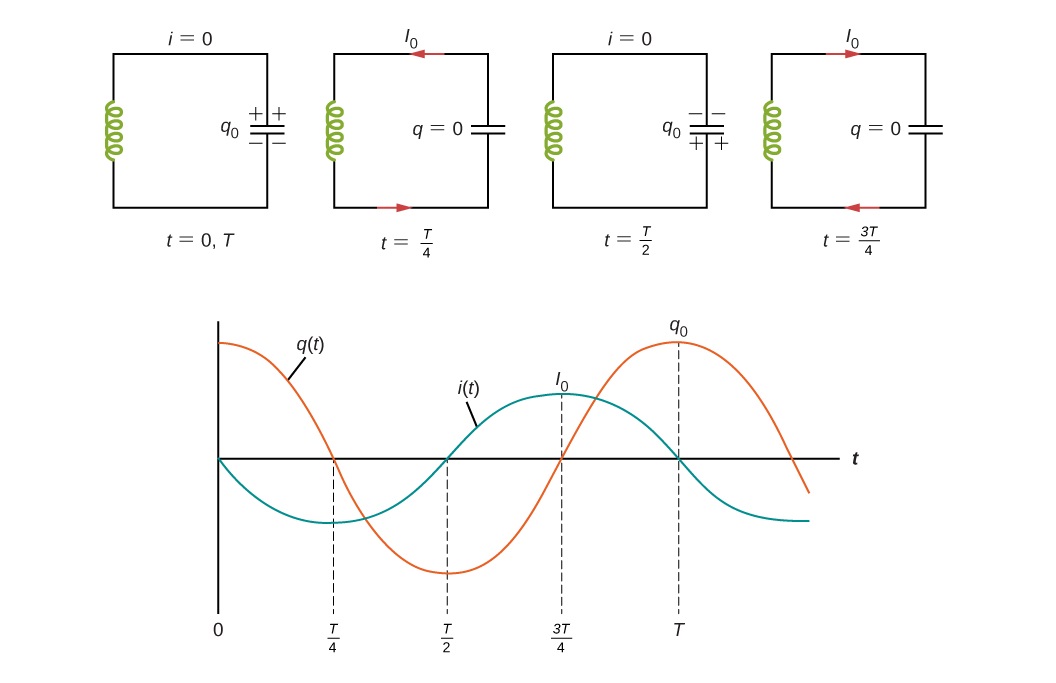
در این آموزش، با معادلات مدارهای الکتریکی و انواع نوسان در مدارهای الکتریکی آشنا خواهیم شد.
معادلات دیفرانسیل مدارهای RLC
در مدارهایی شامل مقاومت ($$R$$)، سلف ($$L$$) و خازن ($$C$$) میتوان نوسانهای الکتریکی را مشاهده کرد.
دو مداری که در این رابطه مورد توجه قرار میگیرند، مدارهای $$RLC$$ سری (شکل ۱) و $$RLC$$ موازی (شکل ۲) هستند.
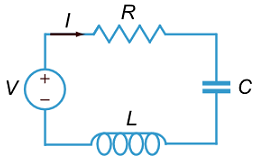
معادلات دیفرانسیل مدار RLC سری
ابتدا، معادلات مدار $$RLC$$ سری را با توصیف تغییرات جریان در مدار $$RLC$$ سری مینویسیم.
ولتاژهای $$V_R$$، $$V_C$$ و $$V_L$$ به ترتیب، اختلاف پتانسیل دو سر مقاومت $$R$$، خازن $$C $$ و سلف $$L$$ را نشان میدهند. روابط این متغیرها به صورت زیر است:
$$ \large { { V _ R } \left ( t \right ) = R I \left ( t \right ) , \; \; \; } \kern-0.3pt { { V _ C } \left ( t \right ) = \frac { 1 } { C } \int \limits _ 0 ^ t { I \left ( \tau \right ) d \tau } , \; \; \; } \kern-0.3pt { { V _ L } \left ( t \right ) = L \frac { { d I } }{ { d t } } . } $$
طبق قانون ولتاژ کیرشهف ($$KVL$$)، داریم:
$$ \large { { V _ R } \left ( t \right ) + { V _ C } \left ( t \right ) } + { { V _ L } \left ( t \right ) } = { E \left ( t \right ) } $$
که در آن، $$E(t)$$ نیروی محرکه الکتریکی (emf) منبع توان است.
وقتی مقدار emf ثابت باشد ($$E$$)، بعد از جایگذاری عبارتهای $$V_R$$، $$V_C$$ و $$V_L$$ در معادله دیفرانسیل و مشتقگیری از این معادله، داریم:
$$ \large { \frac { { { d ^ 2 } I \left ( t \right ) } } { { d { t ^ 2 } } } + \frac { R } { L } \frac { { d I \left ( t \right ) } } { { d t } } } + { \frac { 1 } { { L C } } I \left ( t \right ) } = { 0 . } $$
با تعریف $$ 2 \beta = { \frac { R } { L } \normalsize } $$ و $$ \omega _ 0 ^ 2 = { \frac { 1 } { { L C } } \normalsize } $$، معادله را میتوان به صورت زیر بازنویسی کرد:
$$ \large { \frac { { { d ^ 2 } I } } { { d { t ^ 2 } } } + 2 \beta \frac { { d I } } { { d t } } + \omega _ 0 ^ 2 I } = { 0 . } $$
معادله دیفرانسیل بالا، مشابه معادله نوسانهای میرای جرم متصل به فنر است. بنابراین، نوسان میرا در مدارهای $$RLC$$ با مقادیر خاصی برای پارامترها رخ میدهد.
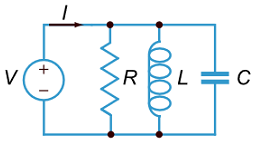
معادلات دیفرانسیل مدار RLC موازی
اکنون مدار $$RLC$$ موازی را در نظر میگیریم و یک معادله دیفرانسیل مشابه را برای آن به دست میآوریم.
با استفاده از قانون جریان کیرشهف ($$KCL$$)، جریان کل گذرنده از مقاومت $$R$$، سلف $$L$$ و خازن $$C$$ (شکل ۲)، به صورت زیر است:
$$ \large { { I _ R }\left ( t \right ) + { I _ L } \left ( t \right ) + { I _ C } \left ( t \right ) } = { I \left ( t \right ) . } $$
که در آن:
$$ \large { { I _ R } = \frac { V } { R } , \; \; \; } \kern-0.3pt { { I _ L } = \frac { 1 } { L } \int \limits _ 0 ^ t { V d \tau } , \; \; \; } \kern-0.3pt { { I _ C } = C \frac { { d V } } { { d t } }} $$
برای حالتی که مجموع جریان ثابت باشد ($$ I\left( t \right) = {I_0} $$)، معادله دیفرانسیل مرتبه دوم برای متغیر $$V$$ به صورت زیر خواهد بود:
$$ \large \begin {align*} { { \frac { V } { R } + \frac { 1 } { L } \int \limits _ 0 ^ t { V d \tau } } + { C \frac { { d V } } { { d t } } = { I _ 0 } , \; \; } } \\ \Rightarrow { { C \frac { { { d ^ 2 } V } } { { d { t ^ 2 } } } + \frac { 1 } { R } \frac { { d V } } { { d t } } } + { \frac { 1 } { L } V = 0 . } } \end {align*} $$
همانگونه که میبینیم، باز هم با معادلهای مواجه خواهیم بود که نوسانهای میرا را نشان میدهد. بنابراین، مد نوسانی در مدار $$RLC$$ سری نیز رخ میدهد.
مدار رزونانس یا تشدید (فرمول تامسون)
در سادهترین حالت، وقتی مقاومت اهمی صفر باشد ($$ R = 0$$) و منبع emf حذف شود ($$E=0$$)، مدار رزونانس، فقط از خازن $$C$$ و سلف $$L$$ تشکیل میشود و با معادله دیفرانسیل زیر توصیف میشود:
$$ \large { \frac { { { d ^ 2 } I } } { { d { t ^ 2 } } } + \omega _ 0 ^ 2 I = 0 , \; \; } \kern-0.3pt {\text{} \; \; \omega _ 0 ^ 2 = \frac { 1 } { { L C } } . } $$
در این مدار، نوسانهای الکتریکی نامیرا با دوره تناوب زیر وجود دارد:
$$ \large { T _ 0 } = \frac { { 2 \pi } } { { { \omega _ 0 } } } = 2 \pi \sqrt { L C } . $$
این فرمول، به افتخار فیزیکدان انگلیسی، ویلیام تامسون (William Thomson) به فرمول تامسون (Thomson Formula) مشهور است که آن را در سال ۱۸۵۳ به دست آورد.
نوسانهای میرا در مدار RLC سری
معادله دیفرانسیل مرتبه دومی که نوسانهای میرا را در مدار $$RLC$$ سری توصیف میکند، به صورت زیر است:
$$ \large { \frac { { { d ^ 2 } I } } { { d { t ^ 2 } } } + \frac { R } { L } \frac { { d I } } { { d t } } } + { \frac { 1 } { { L C } } I } = { 0 . } $$
معادله مشخصه متناظر به فرم زیر است:
$$ \large { \lambda ^ 2 } + \frac { R } { L } \lambda + \frac { 1 } { { L C } } = 0 . $$
ریشههای معادله بالا نیز برابرند با:
$$ \large \begin {align*}
{ { \lambda _ { 1 , 2 } } } & = { \frac { { – \frac { R } { L } \pm \sqrt { \frac { { { R ^ 2 } } } { { { L ^ 2 } } } – \frac { 4 } { { L C } } } } } { 2 } } \\ & = { – \frac { R } { { 2 L } } \pm \sqrt { { { \left ( { \frac { R } { { 2 L } } } \right ) } ^ 2 } – \frac { 1 } { { L C } } } } \\ & = { – \beta \pm \sqrt { { \beta ^ 2 } – \omega _ 0 ^ 2 } } \end {align*} $$
که در آن، $$ \beta = {\frac{R}{{2L}}\normalsize} $$ ضریب میرایی و $$ \omega _0 $$ فرکانس رزونانس مدار است.
بسته به مقادیر $$R$$، $$L$$ و $$C$$ سه حالت مختلف داریم.
حالت ۱: فرامیرا ($$ {R^2} \gt {\large\frac{{4L}}{C}\normalsize} $$)
در این حالت، هر دو ریشه معادله مشخصه $$ \lambda _ 1$$ و $$ \lambda _2$$ حقیقی، مجزا و منفی هستند. پاسخ عمومی معادله دیفرانسیل به صورت زیر است:
$$ \large { I \left ( t \right ) } = { { C _ 1 } { e ^ { { \lambda _ 1 } t } } + { C _ 2 } { e ^ { { \lambda _ 2 } t } } . } $$
در این مورد، جریان به صورت یکنوا به صفر میل میکند (شکل ۳).
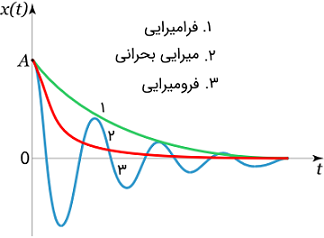
حالت ۲: میرای بحرانی ($$ {R^2} = {\large\frac{{4L}}{C}\normalsize} $$)
این حالت، مرزی یا بحرانی نامیده میشود. در اینجا، ریشههای معادله مشخصه، برابر، حقیقی و منفی هستند. جواب عمومی این حالت، به صورت زیر است:
$$ \large { I \left ( t \right ) = \left ( { { C _ 1 } t + { C _ 2 } } \right ) { e ^ { – \beta t } } } = { \left ( { { C _ 1 } t + { C _ 2 } } \right ) { e ^ { – { \large \frac { R } { { 2 L } } \normalsize} t } } . } $$
در ابتدا، جریان ممکن است حتی افزایش نیز پیدا کند، اما به سرعت به صورت نمایی کاهش پیدا میکند.
حالت ۳: فرومیرا ($$ {R^2} \lt {\large\frac{{4L}}{C}\normalsize} $$)
در این حالت، ریشههای معادله مشخصه مزدوج مختلط هستند و منجر به نوسانهای میرا در مدار میشوند. جریان به صورت زیر به دست میآید:
$$ \large { I \left ( t \right ) } = { { e ^ { – \beta t } } \left ( { A \cos \omega t + B \sin \omega t } \right ) } $$
که در آن، $$ \beta = {\frac{R}{{2L}}\normalsize}$$ ضریب میرایی، و $$ \omega = \sqrt { { \frac { 1 } {{ L C } } \normalsize } – { { \left ( { \frac { R } { { 2 L } } \normalsize } \right ) } ^ 2 } } $$ فرکانس نوسان، و $$A$$ و $$B$$ ثابتهای انتگرالگیری هستند و به شرایط اولیه بستگی دارد. توجه کنید که فرکانس $$\omega$$ کمتر از فرکانس $$\omega _0 $$ رزونانس مدار است. شکل عمومی منحنی $$I(t)$$ در این حالت، در شکل ۳ نشان داده شده است.
نوسانهای اجباری و رزونانس
اگر مدار رزونانس یا تشدید، شامل یک منبع با emf متغیر متناوب باشد، نوسانهای متناوب در سیستم به وجود میآید. اگر نیروی محرکه الکتریکی $$E$$ منبع متغیر به صورت زیر باشد:
$$ \large E \left ( t \right ) = { E _ 0 } \cos \omega t, $$
آنگاه معادله دیفرانسیل نوسانهای اجباری در مدار $$RLC$$ سری را میتوان به صورت زیر نوشت:
$$ \large \begin {align*}
{ { \frac { { { d ^ 2 } q \left ( t \right ) } } { { d {t ^ 2 } } } + \frac { R } { L } \frac { { d q \left ( t \right ) } } { { d t } } } + { \frac { 1 } { { L C } } q \left ( t \right ) } = { \frac { 1 } { L } { E _ 0 } \cos \omega t \; \; } }
\end {align*} $$
یا
$$ \large { { \; \; \frac { { { d ^ 2 } q } } { { d { t ^ 2 } } } + 2 \beta \frac { { d q } } { { d t } } + \omega _ 0 ^ 2 q } = { \frac { { { E _ 0 } } } { L } \cos \omega t } } $$
که در آن، $$q$$ بار خازن است. همچنین تساویهای $$ 2\beta = \frac{R}{L} $$ و $$ \omega _0^2 = \frac{1}{{LC}} $$ نیز برقرارند.
معادله بالا، متناظر با معادله نوسان اجباری یک جسم متصل به فنر است. جواب این معادله، از مجموع جواب عمومی و جواب خصوصی معادله ناهمگن تشکیل میشود. بخش اول، کاهش گذرا است و بعدی، فقط به نیروی خارجی اعمال شده بر مدار بستگی دارد.
نوسانهای اجباری، به صورت زیر خواهند بود:
$$ \large \begin {align*}
q \left ( t \right ) & = \kern0pt { { \frac { { { E _ 0 } } } { { L \sqrt { { { \left ( { \omega _ 0 ^ 2 – { \omega ^ 2 } } \right ) } ^ 2 } + 4 { \beta ^ 2 } { \omega ^ 2 } } } } \cdot } } \kern0pt { { \cos \left ( { \omega t + \varphi } \right ) }} \\ & = { { \frac { { { E _ 0 } } } { { \omega \sqrt { { R ^ 2 } + { { \left ( { \omega L – \frac {1 } { { \omega C } } } \right ) } ^ 2 } } } } \cdot } \kern0pt { \cos \left ( { \omega t + \varphi } \right ) } }
\end {align*} $$
که در آن، $$ \varphi $$ با فرمول زیر تعیین میشود:
$$ \large { \varphi = \arctan \left ( { – \frac { { 2 \beta \omega } } { { \omega _ 0 ^ 2 – { \omega ^ 2 } } } } \right ) } = { \arctan \frac { R } { { \omega L – \frac { 1 } { { \omega C } } } } . } $$
با دانستن تغییر بار $$q (t)$$، به سادگی میتوان جریان را نیز محاسبه کرد:
$$ \large \begin {align*}
I \left ( t \right ) & = \frac { { d q \left ( t \right ) } } { { d t } } = { { – \frac { { { E _ 0 } } } { { \sqrt { { R ^ 2 } + { { \left ( { \omega L – \frac { 1 } { { \omega C } } } \right ) } ^ 2 } } } } \cdot } \kern0pt { \sin \left ( { \omega t + \varphi } \right ) }} \\ & = { { \frac { { { E _ 0 } } } { { \sqrt { { R ^ 2 } + { { \left ( { \omega L – \frac { 1 } { { \omega C } } } \right ) } ^ 2 } } } } \cdot } \kern0pt { \cos \left ( { \omega t – \theta } \right ) } }
\end {align*} $$
که در آن، $$ \theta = – \left( {\varphi + \frac{\pi }{2}} \right)$$. زاویه $$ \theta $$ جابهجایی فاز نوسانهای جریان $$I(t)$$ را نسبت به نوسانات منبع ولتاژ $$ E\left( t \right) = {E_0}\cos \omega t $$ نشان میدهد.
دامنه جریان ($$I_0$$) و جابهجایی فاز ($$ \theta $$) برابرند با:
$$ \large \begin {align*}
{ { I _ 0 } }& = { \frac { { { E _ 0 } } } { { \sqrt { { R ^ 2 } + { { \left ( { \omega L – \frac { 1 } { { \omega C } } } \right ) } ^ 2 } } } } } = { \frac { { { E _ 0 } } } { Z } , \; \; \; } \kern-0.3pt \\ \theta & = \arctan \frac { { \omega L – \frac { 1 } { { \omega C } } } } { R } .
\end {align*} $$
کمیت $$ \sqrt {{R^2} + {{\left( {\omega L – {\frac{1}{{\omega C}}\normalsize}} \right)}^2}}$$، امپدانس یا امپدانس مدار نامیده میشود. امپدانس، از مقاومت اهمی $$R$$ و راکتانس $$ {\omega L – {\frac{1}{{\omega C}}}\normalsize}$$ تشکیل میشود. امپدانس مدار رزونانس، به فرم مختلط به صورت زیر نوشته میشود:
$$ \large Z = R + i \left ( { \omega L – \frac { 1 } { { \omega C } } } \right ) . $$
با توجه به فرمولهای بالا، میتوان دریافت که دامنه نوسان حالت ماندگار، وقتی ماکزیمم است که داشته باشیم:
$$ \large { \omega L = \frac { 1 } { { \omega C } } \; \; \Rightarrow \; \; } \kern-0.3pt { \omega = { \omega _ 0 } = \frac { 1 } { { \sqrt { L C } } } . } $$
در این شرایط، رزونانس در مدار رخ میدهد. فرکانس رزونانس $$ \omega _ 0$$ برابر با فرکانس نوسانهای آزاد در مدار است و به مقاومت $$R$$ بستگی دارد.
میتوانیم فرمول دامنه نوسانهای اجباری را برای به دست آوردن یک وابستگی صریح به نسبت فرکانس $$ \large\frac{\omega }{{{\omega _0}}}\normalsize$$ تبدیل کنیم که در آن، $$ \omega _ 0$$ فرکانس رزونانس است. در نتیجه، داریم:
$$ \large \begin {align*}
\require {cancel} { I _ 0 } & = \frac { { { E _ 0 } } }{ { \sqrt { { R ^ 2 } + { { \left ( { \omega L – \frac { 1 } { { \omega C } } } \right ) } ^ 2 } } } } = { \frac { { \frac { { { E _ 0 } } } { { { \omega _ 0 } } } } } { { \frac { { \sqrt { { R ^ 2 } + { { \left ( { \omega L – \frac { 1 } { { \omega C } } } \right ) } ^ 2 } } } } { { { \omega _ 0 } } } } } } \\ & = { \frac { { \frac { { { E _ 0 } } } { { { \omega _ 0 } } } } } { { \sqrt { \frac { { { R ^ 2 } } } { { \omega _ 0 ^ 2 } } + { { \left ( { \frac { \omega } { { { \omega _ 0 } } } L – \frac { 1 } { { \omega { \omega _ 0 } C } }} \right ) } ^ 2 } } } } } = { \frac { { { E _ 0 } \sqrt { L C } } } { { \sqrt { { R ^ 2 } L C + { { \left ( { \frac { \omega } { { { \omega _ 0 } } } L – \frac { 1 } { { \frac { \omega } { { { \omega _ 0 } } } \frac { \cancel { C } }{ { L \cancel { C } } } } } } \right ) } ^ 2 } } } } } \\ & = { \frac { { { E _ 0 } \sqrt { L C } } } { { \sqrt { { R ^ 2 } L C + { { \left ( { \frac { \omega } { { { \omega _ 0 } } } L – \frac { L }{ { \frac { \omega } { { { \omega _ 0 } } } } } } \right ) } ^ 2 } } } } } = { \frac { { { E _ 0 } \sqrt C } } { { \sqrt { { R ^ 2 } C + { { \left ( { \frac { \omega } { { { \omega _ 0 } } } – \frac { 1 } { { \frac { \omega } { { { \omega _ 0 } } } } }} \right ) } ^ 2 } } } } . }
\end {align*} $$
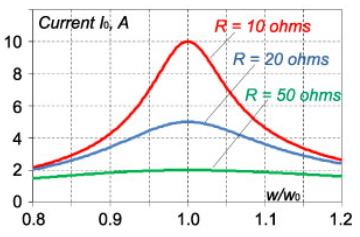
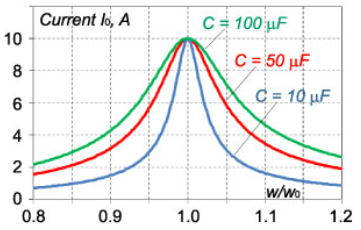
وابستگی دامنه جریان به نسبت فرکانس $$\large\frac{\omega }{{{\omega _0}}}\normalsize $$ برای مقادیر مختلف $$r$$ و $$c$$ در شکلهای 4 و 5 نشان داده شده است. این منحنیها برای پارامترهای $$E = 100\;\text{V}$$، $$ L = 1\;\text{mH}$$، $$ C = 10\;\mu\text{F} $$ (شکل ۴) و $$ R = 10\;\text{ohms} $$ (شکل ۵)، رسم شدهاند.
ویژگیهای رزونانسی یک مدار، با ضریب کیفیت $$Q$$ مشخص میشوند که مقدار عددی آن برابر با نسبت فرکانس رزونانس $$\omega _0$$ به پهنای $$ \Delta \omega $$ مربوط به منحنی رزونانس در $$\large{\frac{1}{\sqrt 2}}\normalsize$$ حداکثر مقدار است (شکل ۶).
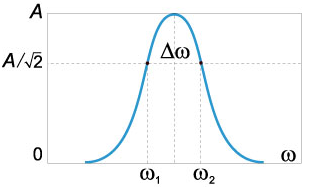
ضریب $$Q$$ در مدار $$RLC$$ سری، به صورت زیر تعریف میشود:
$$ \large Q = \frac { 1 } { R } \sqrt { \frac { L } { C } } . $$
این پارامتر، برای یک مدار $$RLC$$ موازی به صورت زیر خواهد بود:
$$ \large Q = R \sqrt { \frac { C } { L } } . $$
مثالها
در این بخش، چند مثال را بررسی میکنیم.
مثال ۱
یک مدار الکتریکی از ترکیب سری مقاومت $$ R = 100\;\text{ohms} $$ و پیچهای با اندوکتانس $$ L = 50\;\text{H} $$ تشکیل شده است. در لحظه $$t = 0 $$، یک منبع DC با ولتاژ $$ {V_0} = 200\;\text{V} $$ به مدار متصل میکنیم. موارد زیر را به دست آورید:
- جریان $$I(t)$$ مدار؛
- ولتاژ دو سر مقاومت $$ V_R(t)$$ و ولتاژدو سر سلف $$ V _ L ( t) $$.
حل: مدار $$RL$$ سری، با معادله دیفرانسیل زیر توصیف میشود:
$$ \large L \frac { { d I } } { { d t } } + R I = { V _ 0 } . $$
همانطور که میدانیم، پاسخ این معادله، به صورت مجموع پاسخ عمومی معادله همگن $$I_0$$ و پاسخ خصوصی معادله ناهمگن $$I_1$$ است. جواب عمومی معادله
$$ \large L \frac { { d I } } { { d t } } + R I = 0 $$
به صورت زیر است:
$$ \large { I _ 0 } \left ( t \right ) = A { e ^ { – \frac { R }{ L } t } } $$
که در آن، $$A$$ ثابت انتگرالگیری است.
جواب معادله ناهمگن $$I_1$$ متناظر با حالت ماندگار است که در آن، جریان مدار فقط با مقاومت اهمی $$R$$ و به صورت $${I_1} = \frac{{{V_0}}}{R}$$ تعیین میشود. در نتیجه، معادله نهایی جریان به صورت زیر خواهد بود:
$$ \large { I \left ( t \right ) = { I _ 0 } + { I _ 1 } } = { A { e ^ { – \frac { R } { L } t } } + \frac { { { V _ 0 } } } { R } . } $$
ثابت $$A$$ را میتوان با استفاده از شرایط اولیه $$ I\left( {t = 0} \right) = 0$$ تعیین کرد. در نتیجه، داریم:
$$ \large { 0 = A { e ^ { – \frac { R } { L } \cdot 0 } } + \frac { { { V _ 0 } } } { R } , \; \; } \Rightarrow { A = – \frac { { { V _ 0 } } } { R } . } $$
بنابراین، پس از آنکه مدار بسته شود، جریان گذرنده از آن به صورت زیر به دست میآید:
$$ \large \begin {align*}
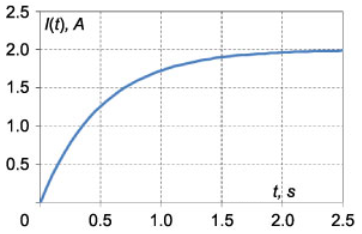
I \left ( t \right ) & = – \frac { { { V _ 0 } } } { R } { e ^ { – \frac { R } { L } t } } + \frac { { { V _ 0 } } } { R } = { \frac { { { V _ 0 } } } { R } \left ( { 1 – { e ^ { – \frac { R } { L } t } } } \right ) } \\ & = { \frac { { 2 0 0 } } { { 1 0 0 } } \left ( { 1 – { e ^ { – \frac { { 1 0 0 } } { { 5 0 } } t } } } \right ) } = { 2 \left ( { 1 – { e ^ { – 2 t } } } \right ) \; \left[ \text {A} \right ] . }
\end {align*} $$
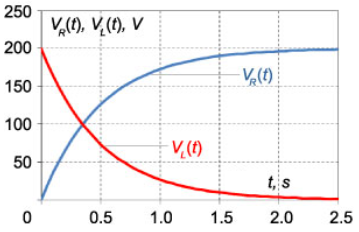
شکل زیر، نمودار $$ I(t)$$ را نشان میدهد.
ولتاژ $$V_R$$ مقاومت و ولتاژ $$V_L$$ سلف با معادلات زیر به دست میآیند:
$$ \large \begin {align*}
{ V _ R } \left ( t \right ) & = I \left ( t \right ) R = { { V _ 0 } \left ( { 1 – { e ^ { – \frac { R } { L } t } } } \right ) } = { 2 0 0 \left ( { 1 – { e ^ { – 2 t } } } \right ) \; \left [ \text {V} \right ],} \\
\require {cancel} { V _ L } \left ( t \right ) & = L \frac { { d I \left ( t \right ) } } { { d t } } = { \frac { { L { V _ 0 } } } { R } \frac { d } { { d t } } \left ( { 1 – { e ^ { – \frac { R } { L } t } } } \right ) } \\ & = { \frac { { \cancel { L } { V _ 0 } } } { \cancel { R } } \cdot \frac { \cancel { R } } { \cancel { L } } { e ^ { – \frac { R } { L } t } } } = { { V _ 0 } { e ^ { – \frac { R } { L } t } } } = { 2 0 0 { e ^ { – 2 t } } \; \left [ \text {V} \right ] . }
\end {align*} $$
منحنیهای توابع $$ {V_R}\left( t \right) $$ و $$ {V_L}\left( t \right) $$ در شکل ۸ نشان داده شدهاند.
مثال ۲
یک مدار الکتریکی، از مقاومت $$ R = 100\;\text{ohms} $$ سری با خازن $$ C = 0.01\;\mu\text{F} $$ تشکیل شده است. در لحظه اولیه، منبع $$DC$$ با ولتاژ $$ {V_0} = 200\;\text{V} $$ به مدار متصل میشود. موارد زیر را به دست آورید:
- جریان $$ I(t)$$ مدار؛
- ولتاژ دو سر مقاومت $$V_R(t)$$ و ولتاژ دو سر خازن $$ V _C (t) $$.
حل: این مثال، مشابه مثال قبل است؛ با این تفاوت که نوع مدار فرق میکند و در اینجا یک مدار $$RC$$ داریم.
طبق قانون جریان کیرشهف، داریم:
$$ \large { V _ R } \left ( t \right ) + { V _ C } \left ( t \right ) = { V _ 0 } $$
که در آن، ولتاژ دو سر مقاومت برابر است با:
$$ \large { { V _ R } \left ( t \right ) = I \left ( t \right ) R } = { R C \frac { { d { V _ C } } } { { d t } } . } $$
در نتیجه، معادله دیفرانسیل زیر برای توصیف حالت گذرای مدار $$RC$$ به دست میآید:
$$ \large R C \frac { { d { V _ C } } } { { d t } } + { V _ C } = { V _ 0 } . $$
جواب این معادله، از مجموع جواب عمومی $$ V_h$$ معادله همگن و یک جواب خصوصی $$V_1$$ معادله ناهمگن محاسبه میشود. جواب عمومی معادله همگن، به صورت زیر است:
$$ \large \begin {align*}
R C \frac { { d { V _ C } } } { { d t } } + { V _ C } = 0 , \; \; & \Rightarrow { \frac { { d { V _ C } } } { {d t } } = – \frac { 1 } { { R C } } { V _ C } , \; \; } \\ & \Rightarrow { \int { \frac { { d { V _ C } } } { { { V _ C } } } } = – \frac { 1 } { { R C } } \int { d t } , \; \; } \\ & \Rightarrow { \ln { V _ C } = – \frac { t }{ { R C } } , \; \; } \Rightarrow { { V _ h } = A { e ^ { – \large \frac { t } { { R C } } \normalsize } } , }
\end {align*} $$
که در آن، $$A$$ ثابت انتگرالگیری است و به شرایط اولیه مدار بستگی دارد.
در اینجا، جواب خصوصی معادله ناهمگن متناظر با شرایط حالت ماندگار $$ {\large\frac{{d{V_C}}}{{dt}}\normalsize} = 0 $$ است. در نتیجه، ولتاژ دو سر مقاومت برابر با صفر خواهد بود و همه ولتاژ به خازن اعمال میشود: $$V_C = V_0$$. بنابراین، ولتاژ خازن را میتوان به صورت زیر نوشت:
$$ \large { V _ C } \left ( t \right ) = A { e ^ { – \large \frac { t } { { R C } } \normalsize } } + { V _ 0 } . $$
برای شرایط اولیه $$ {V_C}\left( {t = 0} \right) = 0 $$، ثابت $$A$$ به صورت زیر به دست میآید:
$$ \large { 0 = A \cdot 1 + { V _ 0 } , \; \; } \Rightarrow { A = – { V _ 0} . } $$
در نتیجه، معادله ولتاژ خازن، برابر است با:
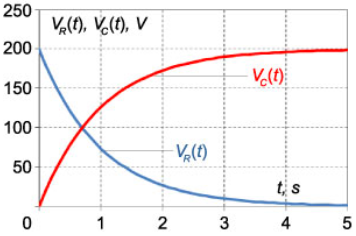
$$ \large \begin {align*}
{ V _ C } \left ( t \right ) & = – { V _ 0 } { e ^ { – \large \frac { t } { { R C } } \normalsize } } + { V _ 0 } = { { V _ 0 } \left ( { 1 – { e ^ { – \large \frac { t } { { R C } } \normalsize } } } \right ) } \\& = { 2 0 0 \left ( { 1 – { e ^ { – t } } } \right ) \; \left [ \text {V} \right ] . }
\end {align*} $$
ولتاژ مقاومت نیز با رابطه زیر بیان میشود:
$$ \large \begin {align*} { V _ R } \left ( t \right ) & = R C \frac { { d { V _ C } } } { { d t } } = { R C { V _ 0 } \frac { d }{ { d t } } \left ( { 1 – { e ^ { – \large \frac { t } { { R C } } \normalsize }} } \right ) } \\ & = { \cancel { R C } { V _ 0 } \cdot \frac { 1 } { \cancel { R C } } { e ^ { – \large \frac { t } { { R C } } \normalsize } } } \\ & = { { V _ 0 } { e ^ { – \large \frac { t } { { R C } } \normalsize } } } = { 2 0 0 { e ^ { – t } } \; \left [ \text {V} \right ] . } \end {align*} $$
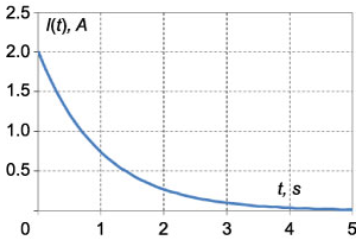
جریان مدار $$RC$$ نیز به صورت زیر به دست میآید:
$$ \large \begin {align*}
I \left ( t \right ) & = \frac { { { V _ R } \left ( t \right ) } } { R } = \frac { { { V _ 0 } } } { R } { e ^ { – \large \frac { t }{ { R C } } \normalsize } } \\ & = \frac { { 2 0 0 } } { { 1 0 0 } } { e ^ { – t } } = 2 { e ^ { – t } } \; \left [ \text {A} \right ] .
\end {align*} $$
منحنیهای $$ {V_C}\left( t \right)$$، $${V_R}\left( t \right)$$ و $$I(t)$$ در شکلهای ۹ و ۱۰ نشان داده شدهاند.
مثال ۳
یک مدار الکتریکی، از مقاومت $$R = 1\;\text{ohms}$$ سری با سلف $$L = 0.25\;\text{H}$$ و خازن $$C = 1\;\mu\text{F}$$ تشکیل شده است. قبل از آنکه دامنه جریان با ضریب $$e$$ کاهش یابد، چه تعداد نوسان انجام شده است؟
حل: در این مدار، نوسانهای میرا با فرکانس زیر رخ میدهد:
$$ \large \omega = \sqrt { \frac { 1 } { { L C } } – \frac { { { R ^ 2 } }} { { 4 { L ^ 2 } } } } . $$
دامنه نوسانها به صورت زیر کاهش مییابد:
$$ \large A \left ( t \right ) = { A_ 0 } { e ^ { – { \large \frac { R } { { 2 L } } \normalsize } t } } . $$
فرض کنید $$N$$ نوسان کامل در مدت زمان $$t$$ رخ دهد:
$$ \large { t = N T = \frac { { 2 \pi N } } { \omega } } = { \frac { { 2 \pi N } } { { \sqrt { \frac { 1 } { { L C } } – \frac { {{ R ^ 2 } } } { { 4 { L ^ 2 } } } } } } . } $$
اگر دامنه به اندازه $$e$$ کاهش یابد، معادله زیر را خواهیم داشت:
$$ \large { – \frac { R } { { 2 L } } t } = { \frac { R } { { 2 L } } \cdot \frac { { 2 \pi N } } { { \sqrt { \frac { 1 } { { L C } } – \frac { { { R ^ 2 } } } {{ 4 { L ^ 2 } } } } } } } = { – 1 . } $$
در نتیجه، تعداد نوسانها به صورت زیر به دست میآید:
$$ \large \begin {align*}
N & = \frac { L } { { \pi R } } \sqrt { \frac { 1 } { { L C } } – \frac { { { R ^ 2 } } } { { 4 { L ^ 2 } } } } = { \frac { 1 }{ \pi } \sqrt { \frac { { { L ^ \cancel { 2 } } } } { { { R ^ 2 } \cancel { L } C } } – \frac { { \cancel { L ^ 2 } \cancel { R ^ 2 } } } { { 4 \cancel { R ^ 2 } \cancel { L ^ 2 } } } } } \\ & = { \frac { 1 } { \pi } \sqrt { \frac { L } { { { R ^ 2 } C } } – \frac {1 } { 4 } } } = { \frac { 1 } { { 2 \pi } } \sqrt { \frac { { 4 L } } { { { R ^ 2 } C } } – 1 } } = { \frac { 1 } { { 2 \pi } } \sqrt { \frac { { 4 \cdot 0 . 2 5 } } { { { 1 ^ 2 } \cdot { { 1 0 } ^ { – 6 } } } } – 1 } } \approx { \frac { { 1 0 0 0 } } { { 2 \pi } } \approx 1 5 9 . }
\end {align*} $$
مثال ۴
یک منبع $$AC$$ را با دامنه $$ {E_0} = 128\;\text{V}$$ و فرکانس $$ \omega = 250\;\text{Hz} $$ به یک مدار سری شامل مقاومت $$ R = 100\;\text{ohms} $$، سلف $$L = 0.4\;\text{H}$$ و خازن $$C = 200\;\mu\text{F} $$ متصل شده است. موارد زیر را به دست آورید:
- دامنه جریان مدار؛
- دامنه ولتاژ روی خازن.
حل: نوسانهای جریان در حالت ماندگار اتفاق میافتد و دامنه آن، برابر است با:
$$ \large \begin {align*}
{ I _ 0 } & = \frac { { { E _ 0 } } } { { \sqrt { { R ^ 2 } + { { \left ( { \omega L – \frac { 1 } { { \omega C } } } \right ) } ^ 2 } } } } = \frac { { 1 2 8 } } { { \sqrt { { { 1 0 } ^ 4 } + { { \left ( { 2 5 0 \cdot 0 . 4 – \frac { 1 } { { 2 5 0 \cdot 0 . 2 \cdot { { 1 0 } ^ { – 3 } } } } } \right ) } ^ 2 } } } } \\ & = \frac { { 1 2 8 } } { { \sqrt { { { 1 0 } ^ 4 } + { { \left ( { 1 0 0 – 2 0 } \right ) } ^ 2 } } } } = \frac { { 1 2 8 } } { { \sqrt { 1 6 4 0 0 } } } \approx { 1 \; \left [ \text {A} \right ] . }
\end {align*} $$
دامنه نوسان ولتاژ خازن نیز برابر است با:
$$ \large { { V _ C } = \frac { { { q _ 0 } } } { C } = \frac { { { I _ 0 } } } { { \omega C } } } = { \frac { 1 } { { 2 5 0 \cdot 0 . 2 \cdot { { 1 0 } ^ { – 3 } } } } } = { 2 0 \; \left [ \text {V} \right ] . } $$
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^










