در مطالب گذشته وبلاگ فرادرس مختصات‌های قطبی را توضیح دادیم. هم‌چنین در ادامه مفاهیم مرتبط با مختصات قطبی هم‌چون انتگرال در این مختصات نیز ارائه شدند. در همین راستا در این مطلب قصد داریم تا در مورد نحوه بدست آوردن مماس در مختصات قطبی بحث کنیم.
خط مماس
به منظور بدست آوردن مماس در ابتدا معادله‌‌ای را در مختصات قطبی به صورت r = f ( θ ) r = f \left ( \theta \right ) r = f ( θ ) d y d x \frac { d y } { d x } d x d y r , θ r,\theta r , θ
x = r cos θ , y = r sin θ \large x = r \cos \theta \ \ , \ \ y = r \sin \theta x = r cos θ , y = r sin θ
با استفاده از تبدیلات فوق، مشتقات را می‌توان بر حسب r , θ r,\theta r , θ
d x d θ = f ′ ( θ ) cos θ − f ( θ ) sin θ d y d θ = f ′ ( θ ) sin θ + f ( θ ) cos θ = d r d θ cos θ − r sin θ = d r d θ sin θ + r cos θ \large \begin{align*}\frac { { dx } } { { d \theta }} & = f'\left( \theta \right)\cos \theta - f\left( \theta \right ) \sin \theta & \hspace {0.75in} \frac { { d y } }{ { d \theta } } & = f'\left( \theta \right)\sin \theta + f \left( \theta \right ) \cos \theta \\ & = \frac { {d r } }{ { d \theta } } \cos \theta - r\sin \theta & \hspace {0.75in} & = \frac{{dr}}{{d\theta }}\sin \theta + r \cos \theta \end{align*} d θ d x = f ′ ( θ ) cos θ − f ( θ ) sin θ = d θ d r cos θ − r sin θ d θ d y = f ′ ( θ ) sin θ + f ( θ ) cos θ = d θ d r sin θ + r cos θ
بنابراین نهایتا مشتقِ d y d x \frac { d y} { d x } d x d y
d y d x = d r d θ sin θ + r cos θ d r d θ cos θ − r sin θ \large \frac {{ d y } }{ { d x } } = \frac { {\displaystyle \frac { {d r} } { { d \theta } } \sin \theta + r \cos \theta } } { {\displaystyle \frac { { dr } } { {d \theta } } \cos \theta - r \sin \theta } } d x d y = d θ d r cos θ − r sin θ d θ d r sin θ + r cos θ
به منظور درک بهتر سخن را کوتاه کرده و به سراغ حل مثال‌ها می‌رویم.
مثال ۱
معادله خط مماس به منحنی r = 3 + 8 sin θ r = 3 + 8\sin \theta r = 3 + 8 sin θ θ = π 6 \displaystyle \theta = \frac{\pi }{6} θ = 6 π
در اولین قدم باید المان‌های موجود در رابطه کلی را بدست آورید. بدین منظور داریم:
d r d θ = 8 cos θ \large \frac { { d r} } { { d \theta } } = 8 \cos \theta d θ d r = 8 cos θ
در نتیجه مشتق d y d x \frac { { d y}} {{ d x } } d x d y
d y d x = 8 cos θ sin θ + ( 3 + 8 sin θ ) cos θ 8 cos 2 θ − ( 3 + 8 sin θ ) sin θ = 16 cos θ sin θ + 3 cos θ 8 cos 2 θ − 3 sin θ − 8 sin 2 θ \large \begin {align*} \frac { { d y } } { { dx } } & = \frac { { 8 \cos \theta \sin \theta + \left( {3 + 8\sin \theta } \right)\cos \theta } } { {8 { { \cos } ^ 2 } \theta - \left( { 3 + 8\sin \theta } \right)\sin \theta } } \\\\ & = \frac { { 16\cos \theta \sin \theta + 3\cos \theta } } { { 8 {{ \cos }^2}\theta - 3\sin \theta - 8 { { \sin } ^ 2 } \theta } } \end {align*} d x d y = 8 cos 2 θ − ( 3 + 8 sin θ ) sin θ 8 cos θ sin θ + ( 3 + 8 sin θ ) cos θ = 8 cos 2 θ − 3 sin θ − 8 sin 2 θ 16 cos θ sin θ + 3 cos θ
بنابراین شیب خط برابر است با:
m = d y d x ∣ θ = π 6 = 4 3 + 3 3 2 4 − 3 2 = 11 3 5 \large m = {\left. { \frac { { d y} } { {d x } } } \right|_{\theta = \frac { \pi } { 6} }} = \frac { {4 \sqrt 3 + \frac { { 3 \sqrt 3 } } { 2} } } { {4 - \frac { 3 } {2 } } } = \frac{{11\sqrt 3 } } { 5 } m = d x d y θ = 6 π = 4 − 2 3 4 3 + 2 3 3 = 5 11 3
با جایگذاری θ \theta θ r r r r = 7 r=7 r = 7 r , θ r,\theta r , θ x , y x,y x , y
x = 7 cos ( π 6 ) = 7 3 2 , y = 7 sin ( π 6 ) = 7 2 \large x = 7\cos \left( {\frac{\pi }{6}} \right) = \frac{{7\sqrt 3 }}{2} \hspace{0.5in} , \hspace{0.5in}y = 7\sin \left ( { \frac { \pi } { 6 } } \right) = \frac{7}{2} x = 7 cos ( 6 π ) = 2 7 3 , y = 7 sin ( 6 π ) = 2 7
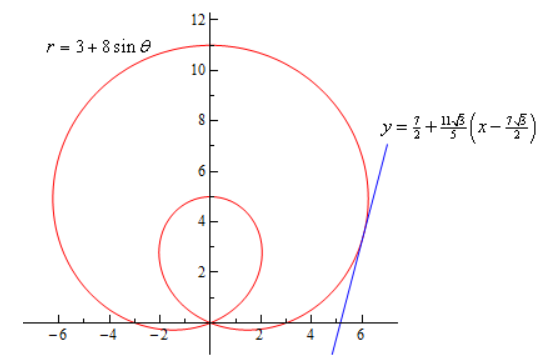
بنابراین معادله خط مماس به این منحنی به صورت زیر بدست می‌آید. در تصویر زیر این منحنی و خط مماس به آن در زاویه مذکور نشان داده شده‌اند.
مثال ۲
معادله خط مماس به منحنی r = sin ( 4 θ ) cos ( θ ) r = \sin \left ( { 4 \theta } \right ) \cos \left ( \theta \right ) r = sin ( 4 θ ) cos ( θ ) θ = π 6 \displaystyle \theta = \frac { \pi } { 6 } θ = 6 π
همانند مثال ۱، مشتق r r r θ \theta θ
d r d θ = 4 cos ( 4 θ ) cos ( θ ) − sin ( 4 θ ) sin ( θ ) \large \frac { {d r } } { { d \theta } } = 4 \cos \left ( { 4 \theta } \right ) \cos \left ( \theta \right ) - \sin \left( { 4 \theta } \right ) \sin \left( \theta \right) d θ d r = 4 cos ( 4 θ ) cos ( θ ) − sin ( 4 θ ) sin ( θ )
در مرحله بعد با استفاده از فرمول ارائه شده، مشتق x x x y y y
d y d x = d r d θ sin θ + r cos θ d r d θ c o s θ − r sin θ = ( 4 cos ( 4 θ ) cos ( θ ) − sin ( 4 θ ) sin ( θ ) ) sin θ + ( sin ( 4 θ ) cos ( θ ) ) cos θ ( 4 cos ( 4 θ ) cos ( θ ) − sin ( 4 θ ) sin ( θ ) ) c o s θ − ( sin ( 4 θ ) cos ( θ ) ) sin θ \large \begin{align*}\frac { {d y } } { { d x } } & = \frac{{\displaystyle \frac{{dr}}{{d\theta } } \sin \theta + r\cos \theta } } { { \displaystyle \frac { { dr } } { { d \theta }}cos\theta - r\sin \theta } } \\ & \\ & = \frac{{\left( {4\cos \left( {4\theta } \right)\cos \left( \theta \right) - \sin \left ( { 4 \theta } \right ) \sin \left( \theta \right)} \right)\sin \theta + \left( {\sin \left( { 4 \theta } \right ) \cos \left( \theta \right)} \right)\cos \theta } } { { \left( {4\cos \left( { 4 \theta } \right)\cos \left( \theta \right) - \sin \left( {4\theta } \right)\sin \left( \theta \right)} \right)cos\theta - \left( {\sin \left( {4\theta } \right)\cos \left( \theta \right)} \right)\sin \theta }}\end{align*} d x d y = d θ d r cos θ − r sin θ d θ d r sin θ + r cos θ = ( 4 cos ( 4 θ ) cos ( θ ) − sin ( 4 θ ) sin ( θ ) ) cos θ − ( sin ( 4 θ ) cos ( θ ) ) sin θ ( 4 cos ( 4 θ ) cos ( θ ) − sin ( 4 θ ) sin ( θ ) ) sin θ + ( sin ( 4 θ ) cos ( θ ) ) cos θ
همان‌طور که می‌بینید رابطه فوق، رابطه‌ای با جملات زیاد است. توجه داشته باشید که معمولا در این روش، عبارت مشتق، پیچیده است. از این رو باید در جایگذاری مقادیر r r r θ \theta θ
d y d x ∣ θ = π 6 = 1 3 3 , r ∣ θ = π 6 = 3 4 \large { \left. {\frac { { d y} } { { dx } } } \right| _ { \theta = \,\frac{\pi }{6}}} = \frac{1}{ { 3 \sqrt 3 } } \hspace {0.4in} , \hspace {0.4in} {\left. r \right|_{\theta = \frac{\pi }{6}}} = \frac { 3} { 4 } d x d y θ = 6 π = 3 3 1 , r ∣ θ = 6 π = 4 3
دلیل بدست آوردن r r r x , y x,y x , y x , y x , y x , y
x = r cos ( θ ) = 3 4 cos ( π 6 ) = 3 3 8 y = r sin ( θ ) = 3 4 sin ( π 6 ) = 3 8 \large x = r \cos \left ( \theta \right ) = \frac { 3 } { 4 }\cos \left( {\frac { \pi } { 6} } \right) = \frac{{3\sqrt 3 } } { 8} \hspace{0.75in} y = r \sin \left( \theta \right) = \frac{ 3 }{ 4 } \sin \left( { \frac{\pi }{6}} \right) = \frac { 3} { 8 } x = r cos ( θ ) = 4 3 cos ( 6 π ) = 8 3 3 y = r sin ( θ ) = 4 3 sin ( 6 π ) = 8 3
با بدست آمدن مقادیر x , y x , y x , y
$$ \large \require {bbox} \bbox[2pt,border:1px solid black]{{y = \frac { 3} { 8 } + \frac { 1 }{ { 3 \sqrt 3 } } \left( {x - \frac { { 3 \sqrt 3 } }{ 8 } } \right) = \frac { 1 }{ { 3\sqrt 3 }}x + \frac{ 1} { 4 } }}$$
مثال ۳
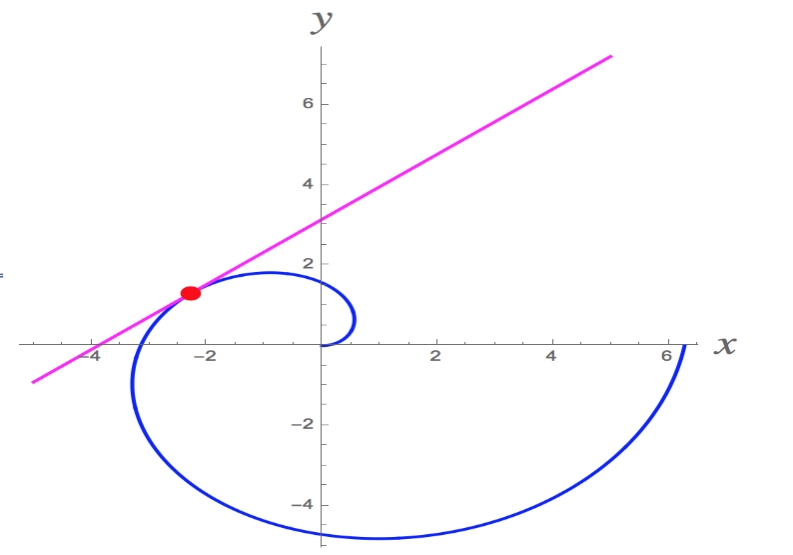
معادله خط مماس به منحنی r = θ − cos ( θ ) r = \theta - \cos \left( \theta \right) r = θ − cos ( θ ) θ = 3 π 4 \displaystyle \theta = \frac { { 3 \pi } } { 4 } θ = 4 3 π
مشتق در مختصات قطبی برابر است با:
d r d θ = 1 + sin ( θ ) \large \frac { {d r } } { { d \theta } } = 1 + \sin \left ( \theta \right ) d θ d r = 1 + sin ( θ )
در نتیجه مشتق در مختصات کارتزین نیز به صورت زیر بدست می‌آید:
d y d x = d r d θ sin θ + r cos θ d r d θ c o s θ − r sin θ = ( 1 + sin ( θ ) ) sin θ + ( θ − cos ( θ ) ) cos θ ( 1 + sin ( θ ) ) c o s θ − ( θ − cos ( θ ) ) sin θ \large \begin{align*}\frac { { dy } } { { d x } } & = \frac{{\displaystyle \frac{{dr}}{ { d \theta } } \sin \theta + r\cos \theta } } { { \displaystyle \frac{{dr}}{{d\theta } } cos \theta - r\sin \theta } } \\ & \\ & = \frac { { \left ( {1 + \sin \left( \theta \right)} \right ) \sin \theta + \left ( { \theta - \cos \left ( \theta \right ) } \right ) \cos \theta } } { { \left( { 1 + \sin \left( \theta \right ) } \right ) cos \theta - \left ( { \theta - \cos \left( \theta \right)} \right)\sin \theta } } \end{align*} d x d y = d θ d r cos θ − r sin θ d θ d r sin θ + r cos θ = ( 1 + sin ( θ ) ) cos θ − ( θ − cos ( θ ) ) sin θ ( 1 + sin ( θ ) ) sin θ + ( θ − cos ( θ ) ) cos θ
همان‌طور که می‌بینید در این حالت نیز به عبارتی پیچیده رسیده‌ایم. مشتق در مختصات کارتزین و مقدار r r r
d y d x ∣ θ = 3 π 4 = 0.2843 , r ∣ θ = 3 π 4 = 3.0633 \large { \left. { \frac { { d y } } { { d x } } } \right|_{\theta = \,\frac { { 3 \pi } } { 4 } }} = 0.2843 \hspace{0.2in} , \hspace{0.2in} {\left. r \right|_{\theta = \frac{ { 3 \pi } }{4 } } } = 3.0633 d x d y θ = 4 3 π = 0.2843 , r ∣ θ = 4 3 π = 3.0633
در نتیجه مختصات‌های کارتزین در این زاویه به صورت زیر قابل محاسبه هستند.
x = r cos ( θ ) = 3.0633 cos ( 3 π 4 ) = − 2.1661 y = r sin ( θ ) = 3.0633 sin ( 3 π 4 ) = 2.1661 x = r \cos \left ( \theta \right ) = 3.0633 \cos \left ( { \frac { { 3 \pi } } { 4} } \right) = - 2.1661 \\ y = r \sin \left ( \theta \right) = 3.0633 \sin \left ( { \frac { { 3 \pi } } { 4 } } \right ) = 2.1661 x = r cos ( θ ) = 3.0633 cos ( 4 3 π ) = − 2.1661 y = r sin ( θ ) = 3.0633 sin ( 4 3 π ) = 2.1661
بنابراین نهایتا معادله خط مماس برابر می‌شود با:
$$\large \require{bbox} \bbox [2pt,border:1px solid black] { { y = 2.1661 + 0.2843 \left ( {x + 2.1661 } \right ) = 0.2843 x + 2.7819 } } $$
در صورت علاقه‌مندی به مباحث در زمینه ریاضیات، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
^^
فرادرس
