آموزش مقیاس بندی ویژگی در پایتون — راهنمای Feature Scaling

اغلب داده‌های در دسترس، قبل از استفاده نیاز به پردازش دارند و نمی‌توانند به صورت مستقیم مورد استفاده قرار بگیرند. یکی از فرآیندهایی که اغلب برای پیش پردازش داده‌ها (Preprocessing) در پروژه‌های داده کاوی و یادگیری ماشین انجام می‌شود، «مقیاس بندی ویژگی» (تغییر مقیاس داده‌ها) یا همان «Feature Scaling» است که با نام «نرمال سازی داده» (Data Normalization) نیز شناخته می‌شود. در این مقاله به آموزش و پیاده‌سازی مقیاس بندی ویژگی در پایتون پرداخته شده است.

مقیاس بندی ویژگی چیست و چه کاربردی دارد؟

برای درک بهتر مفهوم مقیاس بندی ویژگی و پاسخ به این سوال که مقیاس بندی ویژگی یا همان Feature Scaling چیست، بهتر است مثالی ارائه شود.

فیلم آموزش مفاهیم آماری در داده کاوی و پیاده سازی آن در پایتون Python در فرادرس

کلیک کنید

در این مثال فرض می‌شود یک مجموعه داده با 3 ستون و 10 سطر به صورت زیر موجود است:

اگر یک بررسی کلی روی این مجموعه داده انجام شود، مشخص خواهد شد که ستون اول اعدادی بین 23 تا 26 را در بر می‌گیرد؛ درحالی که ستون دوم اعدادی بین 154 تا 210.45 را شامل می‌شود.

فیلم آموزش روش های پیش پردازش داده ها – رایگان در فرادرس

کلیک کنید

این اختلاف بین مقیاس داده‌ها، اغلب مشکلاتی را به وجود می‌آورد که برای رفع آن‌ها نیاز است تا تغییر مقیاس داده‌‌ها یا همان مقیاس بندی ویژگی انجام شود.

روش‌های مقیاس بندی ویژگی چه هستند؟

3 مورد از پرکاربردترین روش‌ها برای مقیاس بندی ویژگی به شرح زیر است:

فیلم آموزش اصول و روش های متن کاوی Text Mining در فرادرس

کلیک کنید

• مقیاس بندی مینیمم-ماکزیمم (Min Max Scaling | Min-Max Normalization)
• مقیاس بندی استاندارد (Standard Scaling)
• مقیاس بندی منسجم (Robust Scaling)

حال در ادامه به معرفی هر یک از روش‌های مقیاس بندی ویژگی در پایتون پرداخته شده است.

مقیاس بندی ویژگی Min Max چیست؟

در روش مقیاس بندی ویژگی Min Max با ضرب و تقسیم داده‌ها به 2 عدد، مقیاس بندی ویژگی بین 0 تا 1 تنظیم می‌شود که به صورت زیر قابل توصیف است:

$$x' =\frac{x - min{(X)}}{max{(X)} - min{(X)}}$$

به این شیوه، همه داده‌های یک ویژگی در مجموعه داده بین صفر و یک تنظیم می‌شوند. حالا در ادامه مقاله آموزش مقیاس بندی ویژگی در پایتون به معرفی و شرح روش مقیاس بندی استاندارد پرداخته شده است.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

معرفی مقیاس بندی ویژگی استاندارد

در روش مقیاس بندی ویژگی استاندارد از واریانس و میانگین استفاده می‌شود. با انجام تغییرات به روش استاندارد، داده‌ها به توزیعی با میانگین صفر و واریانس یک می‌رسند. مقیاس بندی هر یک از داده‌های یک ویژگی با روش مقیاس بندی ویژگی استاندارد به صورت زیر انجام می‌شود:

$$x' =\frac{x - mean(X)}{variance(X)}$$

در روش مقیاس بندی ویژگی استاندارد کمینه و بیشینه داده‌ها به صورت قطعی روی عدد خاصی تنظیم نمی‌شود و تمرکز بر روی تنظیم میانگین و واریانس است.

• مقاله پیشنهادی: واریانس و انحراف معیار | به زبان ساده (+ فیلم آموزش رایگان)

مقیاس بندی ویژگی منسجم چیست؟

در روش مقیاس بندی ویژگی منسجم یا همان Robust Scaling از چارک‌های اول، دوم و سوم داده‌ها استفاده می‌شود. این روش از تغییر مقیاس یا همان مقیاس بندی ویژگی در شرایطی که داده‌های پرت (Outlier) وجود داشته باشد، بسیار کارآمد خواهد بود. رابطه ریاضی موجود برای این تبدیل به صورت زیر است:

$$x' =\frac{x - Q_2(X)}{Q_3(X)-Q_1(X)}$$

در این روش، میانه روی صفر تنظیم می‌شود و فاصله بین چارک اول تا چارک سوم معادل یک واحد خواهد بود.

اکنون زمان آن فرا رسیده است تا وارد محیط برنامه‌نویسی زبان پایتون شده و هر کدام از روش‌های مقیاس بندی ویژگی مورد بررسی قرار بگیرند.

پیاده سازی مقیاس بندی ویژگی در پایتون

برای پیاده سازی مقیاس بندی ویژگی در پایتون (Feature Scaling in Python) ابتدا باید کتابخانه‌های مورد نیاز را فراخوانی کرد. بنابراین در ادامه و بخش بعدی این مقاله، کدهای مربوط به فراخوانی کتابخانه‌ها ارائه شده‌اند.

فیلم آموزش یادگیری ماشین با پایتون – ماشین لرنینگ با Python در فرادرس

کلیک کنید

فراخوانی کتابخانه‌های لازم برای پیاده سازی مقیاس بندی ویژگی در پایتون

برای کدنویسی و پیاده سازی مقیاس بندی ویژگی باید کتابخانه‌هایی برای انجام موارد زیر فراخوانی شوند:

1. کار با آرایه‌ها
2. رسم نمودار
3. پیش پردازش داده

بنابراین، برای پیاده سازی مقیاس بندی ویژگی در پایتون باید هر یک از کتابخانه‌های زیر را فراخوانی کرد:

1. کتابخانه Numpy
2. کتابخانه Matplotlib
3. کتابخانه Scikit-Learn

فیلم آموزش کتابخانه scikit-learn در پایتون – الگوریتم های یادگیری ماشین در فرادرس

کلیک کنید

کدهای مربوط به فراخوانی کتابخانه‌های لازم برای پیاده سازی مقیاس بندی ویژگی در پایتون به صورت زیر است:

1import numpy as np
2import matplotlib.pyplot as plt
3import sklearn.preprocessing as pp

• مقاله پیشنهادی: رسم نمودار در پایتون با Matplotlib — راهنمای کاربردی

اکنون پس از فراخوانی کتابخانه‌های لازم، نوبت به ایجاد مجموعه داده مورد نیاز در محیط برنامه نویسی فرا می‌رسد. لذا در ادامه به آماده‌سازی مجموعه داده برای پیاده سازی مقیاس بندی ویژگی در پایتون پرداخته شده است.

ایجاد مجموعه داده برای پیاده سازی مقیاس بندی ویژگی در پایتون

ایجاد مجموعه داده‌ها برای پیاده سازی مقیاس بندی ویژگی در پایتون به صورت زیر انجام می‌شود:

1Features = ['Age', 'Weight', 'Height']
2X = np.array([[23, 154.25, 67.75],
3             [22, 173.25, 72.25],
4             [22, 154, 66.25],
5             [26, 184.75, 72.25],
6             [24, 184.25, 71.25],
7             [24, 210.25, 74.75],
8             [26, 181, 69.75],
9             [25, 176, 72.5],
10             [25, 191, 74],
11             [23, 198.25, 73.5]])

همان‌طور که در کدهای فوق ملاحظه می‌شود، مجموعه داده مورد نیاز به صورت یک آرایه تعریف شده است. می‌توان نمودار توزیع داده‌ها را نیز رسم کرد.

فیلم آموزش مفاهیم آماری در داده کاوی و پیاده سازی آن در پایتون Python در فرادرس

کلیک کنید

رسم نمودار توزیع داده‌ها

رسم نمودار توزیع داده‌های ایجاد شده برای پیاده سازی مقیاس بندی ویژگی در پایتون به صورت زیر انجام می‌شود:

1for i, f in enumerate(Features):
2    plt.subplot(1, len(Features), i+1)
3    plt.hist(X[:, i], bins=4)
4    plt.xlabel(f)
5    plt.ylabel('N')
6
7plt.show()

در کدهای فوق به ازای هر ویژگی (ستون) در مجموعه داده، یک نمودار جداگانه (Subplot) ایجاد و در آن نمودار هیستوگرام ویژگی مربوطه رسم می‌شود. خروجی کدهای مربوط به رسم نمودار و بصری‌سازی داده‌های ایجاد شده برای پیاده‌سازی مقیاس بندی ویژگی در پایتون به صورت زیر است:

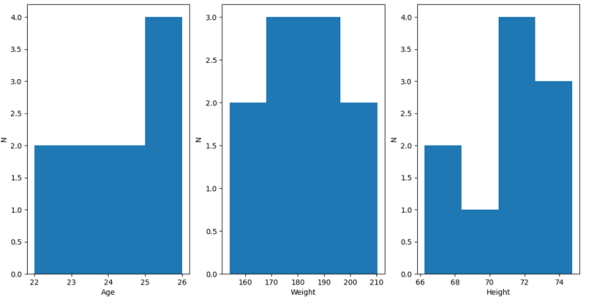
با مصورسازی داده‌ها و رسم نمودار، مشاهده می‌شود که محدوده توزیع و شکل توزیع هر ویژگی به چه صورت است. حال در ادامه به پیاده‌سازی «تنظیم کننده مقیاس کمینه-بیشینه» (Min Max Scaler) روی هر یک از ویژگی‌های مجموعه داده تولید شده پرداخته شده است.

فیلم آموزش کتابخانه Matplotlib برای ترسیم و بصری سازی داده ها در پایتون در فرادرس

کلیک کنید

• مقاله پیشنهادی:
  • رسم نمودار در پایتون با Matplotlib — راهنمای کاربردی
  • هیستوگرام (Histogram) و نمودارهای چگالی — راهنمای بصری سازی داده‌های تک‌ بُعدی در پایتون

پیاده سازی تنظیم کننده مقیاس کمینه بیشینه روی ویژگی‌ها در پایتون

پیاده‌سازی «تنظیم کننده مقیاس کمینه-بیشینه» یا همان «Min-Max Scaler» روی ویژگی‌ها به صورت زیر انجام می‌شود:

1Scaler1 = pp.MinMaxScaler()
2X1 = Scaler1.fit_transform(X)

در کدهای فوق ابتدا یک تنظیم کننده مقیاس (Scaler) تولید و سپس خروجی این تغییر مقیاس در X1 ذخیره می‌شود. حالا برای ملاحظه تغییرات به وجود آمده در ویژگی‌ها می‌توان نمودار داده‌ها را دوباره رسم کرد. نمودار جدید به صورت زیر است:

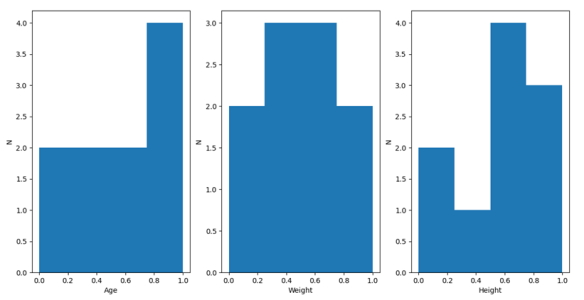
همان‌طور که در نمودار فوق ملاحظه می‌شود، مقادیر تمام ویژگی‌ها در بازه بین صفر تا یک قرار می‌گیرند. حال در ادامه نوبت به پیاده سازی تنظیم کننده مقیاس استاندارد (Standard Scaler) فرا می‌رسد.

پیاده‌سازی تنظیم کننده مقیاس استاندارد روی ویژگی‌ها در پایتون

مشابه روش قبل، یک تنظیم کننده مقیاس، این بار از نوع استاندارد (Standard Scaler) به صورت زیر تولید می‌شود و پس از آن،‌ این تنظیم کننده مقیاس روی داده‌ها پیاده‌سازی و نتیجه در متغیر X2 ذخیره خواهد شد:

1Scaler2 = pp.StandardScaler()
2X2 = Scaler2.fit_transform(X)

حالا برای مشاهده تغییرات انجام شده، بار دیگر می‌توان داده‌ها را مصورسازی و نمودار توزیع آن‌ها را رسم کرد. این نمودار به صورت تصویر زیر خواهد بود:

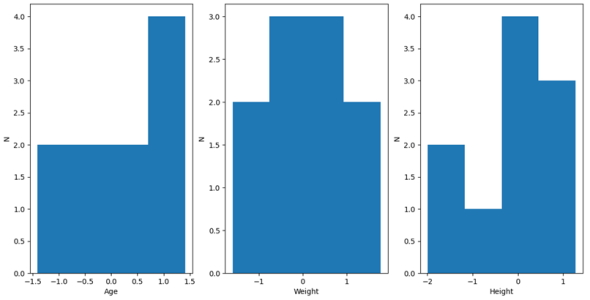
در نمودار فوق ملاحظه می‌شود که با پیاده‌سازی مقیاس بندی ویژگی استاندارد، بازه کمینه و بیشینه برای هر ویژگی در مجموعه داده متفاوت است. با محاسبه میانگین و واریانس برای داده‌های مقیاس بندی شده به صورت استاندارد ملاحظه می‌شود که میانگین‌ها با دقت بالایی به 0 نزدیک شده‌اند و واریانس‌ها روی عدد 1 قرار گرفته‌اند. محاسبه میانگین و واریانس ویژگی‌ها برای X2 به صورت زیر انجام می‌شود:

1M = np.mean(X2, axis=1)
2V = np.var(X2, axis=1)
3
4print(f'{M = }')
5print(f'{V = }')

خروجی کدهای فوق به صورت زیر است:

$$M = array([0.00000000e+00, 6.66133815e-16, 1.07691633e-15])$$

$$V = array([1., 1., 1.,])$$

به این ترتیب همان‌طور که بیان شد، ملاحظه می‌شود که میانگین‌ها با دقت بالایی به 0 نزدیک شده‌اند و واریانس‌ها روی عدد 1 قرار گرفته‌اند. دلیل نامگذاری این روش به نام «Standard Scaler» نیز به مقدار واریانس و میانگین آن مربوط می‌شود که برابر با تابع توزیع استاندارد هستند.

فیلم آموزش مفاهیم آماری در داده کاوی و پیاده سازی آن در پایتون Python در فرادرس

کلیک کنید

اکنون زمان آن فرا رسیده تا سومین روش تنظیم مقیاس ویژگی‌ها در پایتون پیاده سازی شود. بنابراین در ادامه به پیاده‌سازی تنظیم کننده مقیاس منسجم پرداخته شده است.

پیاده‌سازی تنظیم کننده مقیاس منسجم روی ویژگی‌ها در پایتون

پیاده‌سازی تنظیم کننده مقیاس منسجم روی ویژگی‌ها در پایتون نیز مشابه موارد قبلی انجام می‌شود. ابتدا یک تنظیم کننده مقیاس منسجم (Robust Scaler) تولید و سپس اسن Scaler روی داده‌ها اعمال می‌شود:

1Scaler3 = pp.RobustScaler()
2X3 = Scaler3.fit_transform(X)

اکنون پس از پیاده‌سازی تنظیم کننده مقیاس منسجم روی ویژگی‌ها، برای مشاهده تغییرات اعمال شده روی داده‌ها نمودار توزیع X3 رسم می‌شود:

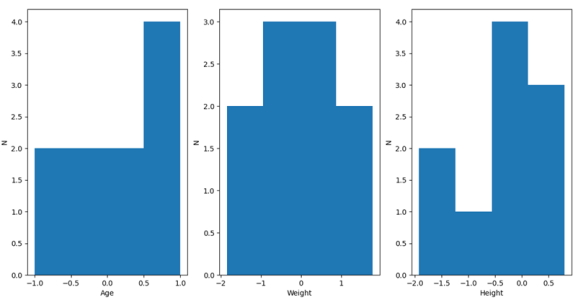
به این ترتیب در نمودار فوق ملاحظه می‌شود که به ازای $$x= median$$ مقدار $$x'$$ برابر با صفر خواهد بود.

نکته مهمی که در مورد Robust Scaler حائز اهمیت است، استفاده از 3 معیار برای تبدیل و همچنین مقاوم بودن آن نسبت به داده‌های پرت است که روش‌هایی مانند Min Max Scaling از این جهت ضعف دارند. برای بررسی‌های بیشتر، می‌توان تنظیمات هرکدام از Scalerها را تغییر داد و تاثیر هر کدام را روی نتایج ملاحظه کرد. برای مثال، تنظیمات زیر می‌توانند تعیین‌کننده باشند:

1. برای Min Max Scaler عامل feature_range قابل تنظیم است.
2. برای Standard Scaler می‌توان عامل‌های with_mean و with_std را تغییر داد.
3. برای Robust Scaler نیز عامل quantile_range را می‌توان تعیین کرد.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

به این ترتیب در اینجا آموزش مقیاس بندی ویژگی در پایتون در این مقاله به پایان رسیده است.

جمع‌بندی

در این مقاله آموزشی روش‌های خطی پرکاربرد برای مقیاس بندی ویژگی‌ها (تغییر مقیاس ویژگی‌ها | Feature Scaling) مورد بررسی قرار گرفتند و اثرات هر کدام روی توزیع و پارامترهای آماری بررسی شدند. علاوه بر روش‌های خطی معرفی شده در این مقاله، روش‌های غیرخطی نیز می‌توانند برای این اهداف مورد استفاده قرار گیرند.