معیار ارزیابی BIC در مدل های احتمالی — از صفر تا صد

برای ارزیابی مدل‌هایی که برمبنای استنباط آماری ایجاد می‌شوند، ابزارها و معیارهای مختلف وجود دارد یکی از این ابزارها، معیار ارزیابی BIC است که میزان اطلاع از دست رفته توسط مدل را مشخص می‌کند. معیار BIC که مخفف Bayesian Information Criterion است، برمبنای تابع درستنمایی محاسبه شده و ارتباط نزدیکی با «معیار ارزیابی آیکاکه» (AIC) دارد.

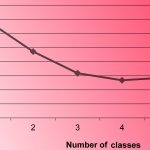
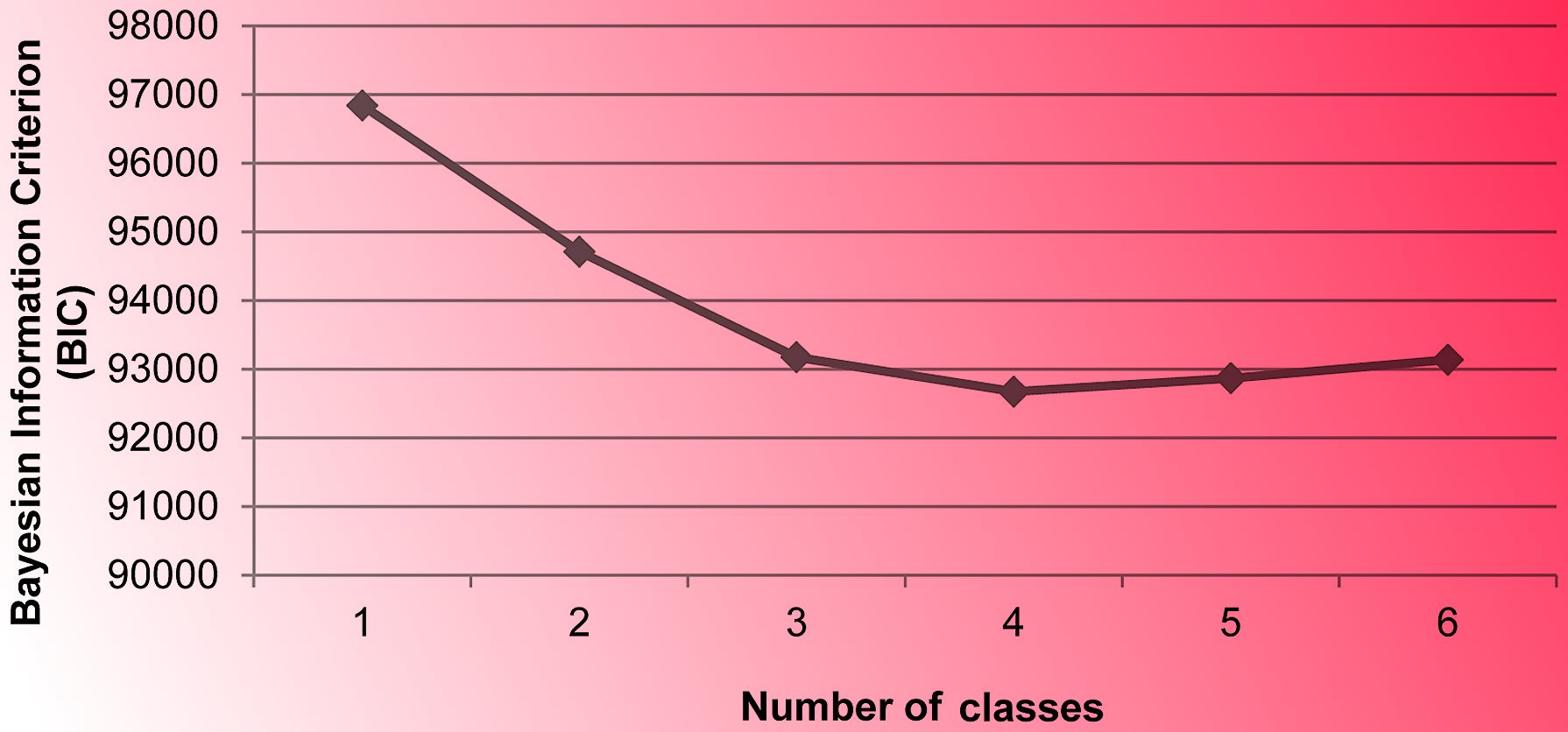
معمولا با افزایش پارامترهای مدل و پیچیده‌تر شدن آن می‌توانیم مقدار تابع درستنمایی را افزایش دهیم که به معنی برازش بهتر داده‌ها و تاییدی بر مدل ارائه شده است. ولی با این کار ممکن است دچار مشکل بیش بردازش شده و اعتبار مدل مخدوش شود. بنابراین استفاده از معیارهایی مانند BIC که علاوه بر میزان درستنمایی به تعداد پارامترها و تعداد مشاهدات نیز توجه دارند، امری مهم تلقی می‌شود. به این ترتیب با توجه به تاثیر تعداد پارامترها و مشاهدات، به همراه تابع درستنمایی، معیار ارزیابی BIC یکی از شاخص‌هایی است که به هر دو وجه برای مناسب بودن مدل یعنی تعداد پارامترها و میزان برازش مدل، توجه داشته و بخصوص در «تئوری اطلاع» (Information Theory) نیز مورد بهره‌برداری قرار می‌گیرد.

همانطور که در ادامه مشاهده خواهیم کرد، معیار ارزیابی BIC به مانند معیار AIC، نمایانگر میزان اطلاعاتی است که توسط مدل از دست رفته است و در نتیجه هر چه مقدار معیار ارزیابی BIC کوچکتر باشد، مدل مورد نظر نسبت به بقیه مدل‌ها، بهتر و مناسب‌تر است. معیار ارزیابی BIC توسط «گیدون شوارتز» (Gideon Schwarz) طی مقاله‌ای که در سال ۱۹۷۸ منتشر کرد، معرفی شد.

از آنجایی که در محاسبه BIC از تابع درستنمایی استفاده می‌شود، برای آشنایی با آن بهتر است ابتدا مطلب تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده را مطالعه کنید. همچنین برای آگاهی از نحوه محاسبه معیار ارزیابی AIC نیز بهتر است نوشتار معیار ارزیابی AIC در مدل های احتمالی — از صفر تا صد را هم بخوانید. با خواندن نوشتار نظریه اطلاع و بی نظمی — آشنایی و مفاهیم اولیه نیز از مفاهیم اولیه نظریه اطلاع و مبانی آن مطلع خواهید شد. همچنین خواندن نوشتارهای معیار واگرایی کولبک لیبلر (Kullback Leibler)— پیاده سازی در پایتون و اعتبار سنجی متقابل (Cross Validation) — به زبان ساده نیز خالی از لطف نیستند.

معیار ارزیابی BIC در مدل های احتمالی

نحوه محاسبه BIC درست به مانند معیار ارزیابی AIC است. با این تفاوت که میزان جریمه برای تعداد پارامترها در مدل بیشتر است. فرض کنید که حداکثر تابع درستنمایی را برای یک مدل آماری با $$\widehat{L}$$، تعداد پارامترها را با $$k$$ و تعداد مشاهدات را هم با $$n$$‌ نشان دهیم.

فیلم آموزش خوشه بندی K میانگین K-Means با اس پی اس اس SPSS در فرادرس

کلیک کنید

در این صورت معیار BIC برای این مدل به صورت زیر محاسبه می‌شود.

$$\large \displaystyle \mathrm {BIC} =k\ln(n)-2\ln({\widehat {L}})$$

رابطه ۱

توجه دارید که در اینجا $$x$$ بیانگر همه مشاهدات بوده و $$\widehat{\theta}$$‌ نیز مقداری از پارامتر است که تابع درستنمایی را در مدل $$M$$ بیشینه می‌کند.

$$\large{\displaystyle {\hat {L}}=p(x\mid {\widehat {\theta }},M)}$$

می‌توان نشان داد که براساس آمار و قضیه بیز رابطه زیر برای تابع توزیع احتمال داده‌ها و مشاهدات $$x$$ و تابع توزیع پیشین پارامتر $$\theta$$‌ برقرار است.

$$\large {\displaystyle p(x\mid M)=\int p(x\mid \theta ,M)\pi (\theta \mid M)\,d\theta }$$

واضح است که در این رابطه، $$\pi(\theta|M)$$ همان توزیع پیشین پارامتر $$\theta$$ در مدل $$M$$‌ است. حال لگاریتم تابع درستنمایی یعنی $${\displaystyle \ln(p(x|\theta ,M))}$$ را براساس بسط تیلور مرتبه دوم نوشته و به شکل زیر نمایش می‌دهیم.

$$\large {\displaystyle \ln(p(x\mid \theta ,M))=\ln({\widehat {L}})-0.5(\theta -{\widehat {\theta }})^Tn{\mathcal {I}}(\theta )(\theta -{\widehat {\theta }})+R(x,\theta )}$$

در اینجا $$\mathcal{I}(\theta)$$ میانگین «اطلاع برای هر یک از مشاهدات» (observed information per observation) برحسب «اطلاع فیشر» (Fisher Information) است. البته توجه داشته باشید که منظور از $$^T$$ نیز  همان ترانهاده بردار پارامترها در حالت چند بُعدی است. براساس محاسبات تقریبی و چشم پوشی کردن از عبارت $$R(x,\theta)$$ و خطی بودن تابع توزیع پیشین حول $$\widehat{\theta}$$، رابطه زیر را خواهیم داشت.

$$\large {\displaystyle p(x\mid M)\approx {\hat {L}}(2\pi /n)^{k/2}|{\mathcal {I}}({\widehat {\theta }})|^{-1/2}\pi ({\widehat {\theta }})}$$

اگر تعداد مشاهدات زیاد باشد بطوری که بتوان از عبارت $$|\mathcal{I}$$ و $$\pi(\theta)$$ نیز چشم پوشی کرد، می‌توان رابطه قبلی را به صورت زیر بازنویسی کرد.

$$\large {\displaystyle p(x\mid M)=\exp\{\ln {\widehat {L}}-(k/2)\ln(n)+O(1)\}=\exp(-\mathrm {BIC} /2+O(1))}$$

به این ترتیب تابع توزیع پسین را به شکل زیر می‌نویسیم  که در آن $$BIC$$ طبق رابطه ۱ حاصل می‌شود.

$$\large {\displaystyle p(M\mid x)\propto p(x\mid M)p(M)\approx \exp(-\mathrm {BIC} /2)p(M)}$$

خصوصیات معیار ارزیابی BIC

هر چند محاسبه معیار ارزیابی BIC به نظر پیچیده می‌رسد ولی می‌توانیم خصوصیات آن را مطابق با لیست زیر فهرست کنیم.

• معیار ارزیابی BIC مستقل از توزیع پیشین است. بنابراین ارزیابی بوسیله آن بدون در نظر گرفتن تابع توزیع پیشین برای پارامتر امکان پذیر است.
• معیار BIC، میزان کارایی مدل را با توجه به تعداد پارامترها و قدرت پیش‌بینی داده‌ها ارزیابی می‌کند.
• تعداد پارامترها و همینطور تعداد مشاهدات در محاسبه BIC‌ نقش داشته و تابع درستنمایی توسط این دو مشخصه جریمه می‌شوند تا از بروز بیش‌برازش جلوگیری شود.
• از معیار BIC می‌توان برای تعیین تعداد خوشه‌های مناسب در الگوریتم‌های «خوشه‌بندی تفکیکی» (Partitional Clustering) استفاده کرد.
• معیار ارزیابی BIC ارتباط زیادی با معیار ارزیابی AIC دارد.
• اگر تعداد مشاهدات بسیار بیشتر از تعداد پارامترها باشد، استفاده از معیار BIC مناسب بوده و تقریبی که در محاسبات بالا به آن اشاره شد، موثرتر خواهد بود.
• از معیار BIC برای تحلیل و انتخاب ویژگی در داده‌های با ابعاد بزرگ نمی‌توان استفاده کرد.

شمارش تعداد پارامترها

مدل‌های آماری برحسب پارامترها، مشخص و این پارامترها نیز توسط مشاهدات برآورد می‌شوند. برای مثال در یک مدل رگرسیون خطی ساده که براساس یک متغیر وابسته و مستقل شکل می‌گیرد، رابطه پارامتری بین متغیرهای مستقل و وابسته به صورت زیر نوشته می‌شود.

$$\large {\displaystyle y_i=b_0+b_1x_i+\epsilon_i}$$

به نظر می‌رسد که در این مدل، یک متغیر مستقل به نام $$x$$ وجود داشته و پارامتر مدل $$b_0$$ و $$b_1$$ برای ایجاد رابطه این متغیر با متغیر وابسته یعنی $$y$$ به کار رفته‌اند. از طرفی واریانس جمله خطا نیز باید برآورد شود تا خصوصیات عبارت یا جمله خطا که میانگینی برابر با صفر دارد نیز مشخص شود. بنابراین تعداد پارامترها یا مقدار $$k=3$$ خواهد بود.

محاسبه معیار ارزیابی BIC برای خوشه‌بندی k-میانگین

در شیوه و الگوریتم‌ خوشه‌بندی k-میانگین» (K-means) از «فاصله اقلیدسی» (Euclidean Distance) بین نقاط استفاده شده و سعی می‌شود که فاصله بین نقطه‌ها در هر خوشه کمینه شود. در این حالت به منظور نمایش و اندازه‌گیری میزان مناسب بودن خوشه‌ها، به جای استفاده از تابع درستنمایی، از فاصله استاندارد شده نقاط و مراکز هر خوشه استفاده می‌شود.

فیلم آموزش آمار و کاربرد آن در مدیریت 1 در فرادرس

کلیک کنید

واضح است که برای استاندارد کردن این نقطه‌ها باید میانگین و انحراف معیار برای هر خوشه نیز محاسبه شود. معیار BIC برای ارزیابی نتیجه خوشه‌بندی k-میانگین با توجه به تعداد خوشه‌ها مطابق با رابطه ۲ محاسبه می‌شود.

$$\large {\displaystyle BIC(k)=\sum_{l=1}^k\sum_{x \in c_l}\left(\dfrac{x-\mu_{cl}}{\sigma_{cl}} \right)^2+k\ln(n)}$$

رابطه ۲

در اینجا $$\mu_{cl}$$‌ مرکز خوشه $$l$$ام و $$\sigma_{cl}$$‌ نیز انحراف معیار آن است. مشخص است که $$k$$‌ تیز تعداد خوشه‌ها و $$n$$‌، تعداد مشاهدات را نشان می‌دهد. به نظر می‌رسد که در این رابطه تابع درستنمایی به کار نرفته است. البته این امر به علت اینکه توزیع داده‌ها مشخص نیست کاملا صحیح است. ولی باید به یاد داشت که منظور از بیشینه تابع درستنمایی در شیوه محاسبه BIC، تعیین مقداری است که به واسطه آن میزان برازش داده‌ها با مدل، اندازه‌گیری شود.

در روش‌های خوشه‌بندی داده‌ها، یکی از ملاک‌ها برای تعیین خوشه‌بندی مناسب، تعیین مقدار مجموع مربعات فاصله نقاط از مرکز هر خوشه است که به نوعی تابع هدف در خوشه‌بندی k-میانگین محسوب می‌شود. در الگوریتم خوشه‌بندی k-میانگین باید این تابع هدف کمینه شود. به همین ترتیب در محاسبه BIC به جای تابع درستنمایی از مجموع مربعات فاصله نقاط از میانگین هر خوشه استفاده می‌شود تا برازش مدل خوشه‌بندی برحسب تعداد خوشه‌ها اندازه‌گیری شود. واضح است که این مقدار بوسیله تعداد مشاهدات و تعداد پارامترها (تعداد خوشه‌ها) جریمه شده است تا از بیش‌برازش جلوگیری شود. در نتیجه از رابطه ۲ می‌توان برای تعیین تعداد خوشه‌های مناسب در هنگام استفاده از الگوریتم k-میانگین استفاده کرد. به این ترتیب $$k$$ را مقداری در نظر می‌گیریم که در آن BIC کمینه شود.

فرض کنید برای یک نمونه داده فرضی باید عمل خوشه‌بندی با الگوریتم k-میانگین صورت بگیرد ولی تعداد خوشه مناسب از قبل مشخص نیست. برای استفاده از محاسبه شاخص BIC یا مشابه آن AIC می‌توان مقدار $$k$$ را پیدا کرد که برای آن میزان واریانس یا همان مجموع مربع فاصله نقاط از مراکز خوشه‌ها کمترین مقدار را دارد. البته واضح است که هر چه تعداد خوشه‌ها بیشتر شود، میزان واریانس درون خوشه‌ها کاهش می‌یابد ولی از طرفی مقدار جریمه معیار BIC و AIC از این امر جلوگیری می‌کنند که تعداد خوشه‌ها بسیار زیاد شوند. تصویر زیر چنین حالتی را نشان می‌دهد.

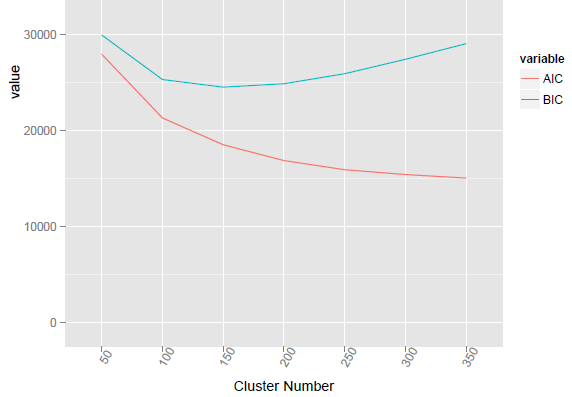
در نمودار بالا، محور افقی تعداد خوشه‌ها و محور عمودی نیز مقدار BIC را نشان می‌دهد. بنابراین به نظر می‌رسد جایی که «منحنی BIC کمترین مقدار را نشان می‌دهد، مقدار بهینه برای تعداد خوشه‌ها است. بنابراین اگر تعداد خوشه‌ها را مقداری بین ۱۰۰ تا ۲۰۰ انتخاب کنیم، معیار BIC  کمینه خواهد بود.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش تخمین خطای طبقه بندی یا Classifier Error Estimation
• مجموعه آموزش‌های داده‌‌کاوی و یادگیری ماشین
• بیش برازش (Overfitting)، کم برازش (Underfitting) و برازش مناسب — مفهوم و شناسایی
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده
• خوشه بندی k میانگین (k-means Clustering) — به همراه کدهای R

^^