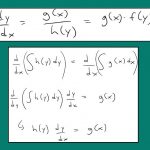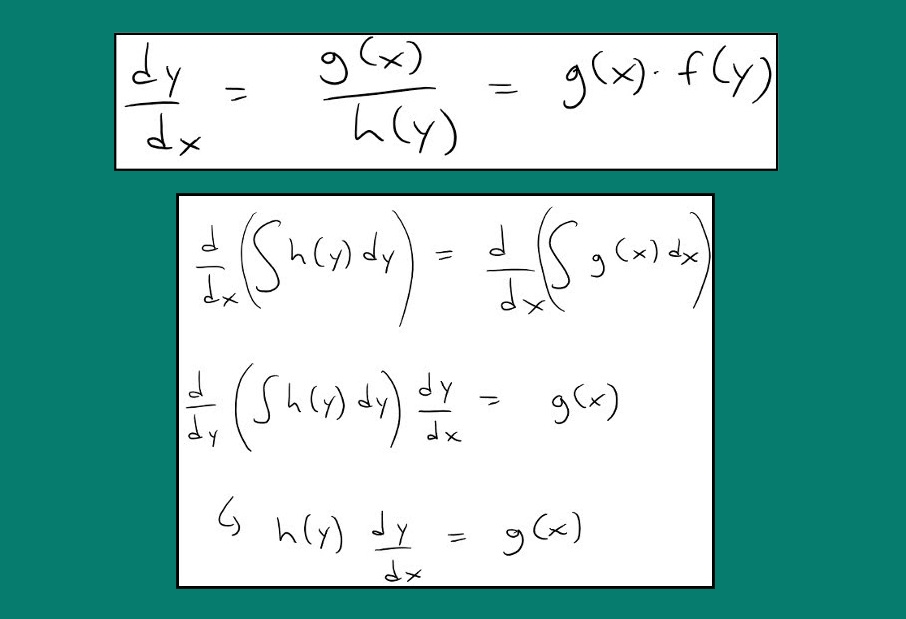معادله دیفرانسیل جدا شدنی — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزش‌های قبلی مجله فرادرس، با معادلات دیفرانسیل آشنا شدیم. در این آموزش‌ها، روش‌های حل معادلات دیفرانسیل مرتبه اول، معادلات دیفرانسیل مرتبه دوم و معادلات مرتبه بالاتر را معرفی کردیم. همچنین به روش حل معادلات خاص، مانند معادله دیفرانسیل چبیشف پرداختیم. در این آموزش، «معادله دیفرانسیل جدا شدنی» (Separable Differential Equation) معرفی، و روش حل آن‌ را بیان خواهیم کرد.

معادله دیفرانسیل جدا شدنی

معادله دیفرانسیل مرتبه اول $$y’ = f\left( {x,y} \right)$$ را یک معادله جداشدنی می‌نامیم اگر بتوان تابع $$f\left( {x,y} \right)$$ را به‌صورت ضرب دو تابع از $$x$$ و $$y$$ نوشت:

$$\large f \left( { x , y } \right) = p \left( x \right) h \left( y \right) ,$$

که در آن $$p (x )$$ و $$h ( y )$$ توابعی پیوسته هستند.

مشتق $${y’}$$ را به‌صورت نسبت دیفرانسیلی $${\large\frac{{dy}}{{dx}}\normalsize}$$ در نظر بگیرید. عبارت $$dx$$ را به سمت راست تساوی انتقال داده و معادله را بر $$h(y)$$ تقسیم می‌کنیم:

$$\large { \frac { { d y } } { { d x } } = p \left( x \right) h \left ( y \right) , } \Rightarrow { \frac { { d y } } { { h \left ( y \right ) } } = p \left ( x \right ) d x . }$$

البته باید مطمئن باشیم که $$h\left( y \right) \ne 0$$. اگر عدد $$x_ 0$$ وجود داشته باشد به‌گونه‌ای که $$h\left( {{x_0}} \right) = 0$$، آن‌گاه این عدد یک جواب برای معادله دیفرانسیل است. تقسیم بر $$h(y)$$ سبب از دست رفتن این جواب می‌شود.

با نوشتن $$q\left( y \right) = {\large\frac{1}{{h\left( y \right)}}\normalsize}$$، معادله به‌صورت زیر درخواهد آمد:

$$\large q \left ( y \right ) d y  = p \left ( x \right ) d x .$$

اکنون که متغیرها را جدا کرده‌ایم، می‌توانیم از معادله انتگرال بگیریم:

$$\large { \int  { q \left ( y \right ) d y } } = { \int { p \left ( x \right ) d x }   } + { C }$$

که در آن، $$C$$ ثابت انتگرال‌گیری است.

با محاسبه انتگرال، خواهیم داشت:

$$\large Q \left ( y \right ) = P \left ( x \right ) + C$$

که جواب عمومی معادله دیفرانسیل جداشدنی را نشان می‌دهد.

مثال‌ها

در ادامه، چند مثال را برای آشنایی بهتر با روش حل معادلات جداشدنی بررسی می‌کنیم.

مثال ۱

معادله دیفرانسیل $${ \large \frac { { d y } } { { d x } } \normalsize } = y \left ( { y + 2 } \right )$$ را حل کنید.

حل: در معادله بالا، $$p\left( x \right) = 1$$ و $$h \left ( y \right ) = h \left ( y \right ) = y \left ( { y + 2 } \right )$$ است. معادله را بر $$h\left( y \right)$$ تقسیم می‌کنیم و $$dx$$ را به سمت راست انتقال می‌دهیم:

$$\large \frac { { d y } } { { y \left ( { y + 2 } \right ) } } = d x .$$

لازم به ذکر است که بعد از تقسیم، می‌توان گفت وقتی $$h(y)$$ صفر می‌شود،‌ $$y=0$$ و $$y=-2$$ جواب‌های معادله هستند. برای مثال، $$y=0$$ را در نظر بگیرید. واضح است که داریم:

$$\large y = 0,\;\;dy = 0.$$

با جایگذاری روابط بالا در معادله، خواهیم داشت: $$0 = 0$$. بنابراین، $$y=0$$ یکی از جواب‌های معادله است. به‌طریق مشابه می‌توان جواب بودن $$y= -2$$ را نیز بررسی کرد.

به معادله دیفرانسیل برمی‌گردیم و از آن انتگرال می‌گیریم:

$$\large { \int { \frac { { d y } } { { y \left ( { y + 2 } \right ) } } } } = { \int { d x } + C . }$$

انتگرال سمت چپ را می‌توان با استفاده از تجزیه کسر انتگرال‌ده محاسبه کرد:

$$ \large { \frac { 1 } { { y \left ( { y + 2 } \right ) } } = \frac { A } { y } + \frac { B } { { y + 2 } } , \; \; } \Rightarrow<br /> { \frac { 1 } { { y \left ( { y + 2 } \right ) } } = \frac { { A \left ( { y + 2 } \right ) + B y } } { { y \left ( { y + 2 } \right ) } } , \; \; }\\ \large \Rightarrow<br /> { 1 \equiv A y + 2 A + B y , \; \; } \Rightarrow<br /> { 1 \equiv \left ( { A + B } \right ) y + 2 A , \; \; } \Rightarrow<br /> { \left \{ { \begin {array} { * { 2 0 } { c } }<br /> { A + B = 0 }\\<br /> { 2 A = 1 }<br /> \end {array} } \right . , \; \; } \Rightarrow<br /> { \left\{ { \begin {array} { * { 2 0 } { c } }<br /> { A = \frac { 1 } { 2 } } \\<br /> { B = – \frac { 1 } { 2 } }<br /> \end {array} } \right . . } $$

تجزیه انتگرال‌ده به کسرهای جزئی به‌صورت زیر است:

$$\large { \frac { 1 } { { y \left ( { y + 2 } \right ) } } } = { \frac { 1 } { 2 } \left ( { \frac { 1 } { y } – \frac { 1 } { { y + 2 } } } \right ) . }$$

بنابراین، داریم:

$$\large { { \frac { 1 } { 2 }\int { \left ( { \frac { 1 } { y } – \frac { 1 } { { y + 2 } } } \right ) d y } } = { \int { d x } + C , \;\; } } \Rightarrow { { \frac { 1 } { 2 } \left ( { \int { \frac { { d y } } { y } } – \int { \frac { { d y } } { { y + 2 } } } } \right ) } = { \int { d x } + C , \;\; } } \\ \large \Rightarrow { { \frac { 1 } { 2 } \left ( { \ln \left | y \right | – \ln \left | { y + 2 } \right | } \right ) } = { x + C , \;\; } } \Rightarrow { \frac { 1 } { 2 } \ln \left | { \frac { y } { { y + 2 } } } \right| = x + C,\;\;}\Rightarrow {\ln \left| {\frac{y}{{y + 2}}} \right| = 2x + 2C.}$$

ثابت را به‌صورت $$2C = {C_1}$$ می‌نویسیم. جواب نهایی معادله به‌فرم زیر خواهد بود:

 $$\large {\ln \left| {\frac{y}{{y + 2}}} \right| = 2x + {C_1},\;\;\;}\kern-0.3pt{y = 0,\;\;\;}\kern-0.3pt{y = – 2.}$$

جواب معادله به‌صورت ضمنی است. در این حالت می‌توان عبارت بالا را به‌صورت تابع صریح $$y = f\left( {x,{C_1}} \right)$$ نوشت که $$C_1$$ یک ثابت است. البته این کار برای همه معادلات دیفرانسیل امکان‌پذیر نیست.

مثال ۲

جواب معادله دیفرانسیل $$\left( {{x^2} + 4} \right)y’ = 2xy$$ را محاسبه کنید.

حل: معادله را به‌فرم زیر می‌نویسیم:

$$\large \left ( { { x ^ 2 } + 4 } \right ) d y = 2 x y d x .$$

هردو سمت معادله را بر $$\left( {{x^2} + 4} \right)y$$ تقسیم می‌کنیم. بنابراین، داریم:

$$\large \frac { { d y } } { y } = \frac { { 2 x d x } } { { \left ( { { x ^ 2 } + 4 } \right ) } } .$$

مشخص است که برای همه $$x$$های حقیقی $${{x^2} + 4} \ne 0$$ است. بررسی می‌کنیم که آیا $$y = 0$$ جواب معادله هست یا خیر. بنابراین، $$y=0$$ و $$dy=0$$ را در معادله دیفرانسیل جایگذاری می‌کنیم. می‌بینیم که $$y=0$$ یکی از جواب‌های معادله است.

اکنون از معادله انتگرال می‌گیریم:

$$\large { { \int { \frac { { d y } } { y } } } = { \int { \frac { { 2 x d x } } { { \left( { { x ^ 2 } + 4 } \right ) } } } } + { C , \;\; } } \Rightarrow { { \ln \left | y \right | } = { \int { \frac { { d \left ( { { x ^ 2 } } \right ) } } { { { x ^ 2 } + 4 } } } } + { C . } }$$

می‌دانیم که $$d\left( {{x^2}} \right)$$ است. بنابراین:

$$\large { \ln \left | y \right | = \int { \frac { { d \left ( { { x ^ 2 } + 4 } \right ) } } { { { x ^ 2 } + 4 } } } + C , \;\; } \Rightarrow { \ln \left | y \right | = \ln \left ( { { x ^ 2 } + 4 } \right ) + C . }$$

ثابت $$C$$ را به‌صورت $$\ln {C_1}$$ می‌نویسیم که در آن، $${C_1} \gt 0$$ است. در نتیجه:

$$\large { \ln \left | y \right | = \ln \left ( { { x ^ 2 } + 4 } \right ) + \ln { C _ 1 } ,\;\; }\Rightarrow { \ln \left | y \right | = \ln \left ( { { C _ 1 } \left ( { { x ^ 2 } + 4 } \right ) } \right ) , \;\; }\\ \large \Rightarrow { \left | y \right | = { C _ 1 } \left ( { { x ^ 2 } + 4 } \right ) , \;\; } \Rightarrow { y = \pm { C _ 1 } \left ( { { x ^ 2 } + 4 } \right ) . }$$

بنابراین، جواب معادله دیفرانسیل به‌صورت زیر خواهد بود:

$$\large { y = \pm { C _ 1 } \left ( { { x ^ 2 } + 4 } \right ) , \;\;}\kern-0.3pt { y = 0 , \;\;}\kern-0.3pt { \text{,}\;\;}\kern-0.3pt { { C _ 1 } \gt 0.}$$

این جواب را می‌توان ساده‌تر کرد. درواقع، اگر از ثابت دلخواه $$C$$ استفاده کنیم که مقدار آن بین $$-\infty$$ و $$\infty$$ است، داریم:

$$\large y = C \left ( { { x ^ 2 } + 4 } \right ) .$$

اگر $$C = 0$$ باشد، $$y=0$$ است.

مثال ۳

تمام جواب‌های معادله $$y’ = – x{e^y}$$ را بیابید.

حل: معادله را به‌صورت زیر می‌نویسیم:

$$\large { \frac { { d y } } { { d x } } = – x { e ^ y } , \;\; } \Rightarrow { \frac { { d y } } { { { e ^ y } } } = – x d x , \;\; } \Rightarrow { { e ^ { – y } } d y = – x d x . }$$

واضح است که اگر معادله بر $$e^y$$ تقسیم کنیم، از آنجایی که $${e^y} \gt 0$$ است، سبب از دست رفتن جواب‌ها نمی‌شود. بعد از انتگرال‌گیری داریم:

$$\large { \int { { e ^ { – y } } d y } = \int { \left ( { – x } \right ) d x } + C , \;\; } \\ \large \Rightarrow { – { e ^ { – y } } = – \frac { { { x ^ 2 } } } { 2 } + C \;\;}\Rightarrow {\;\;}\kern0pt { { e ^ { – y } } = \frac { { { x ^ 2 } } } { 2 } + C . }$$

جواب را می‌توان به‌فرم صریح زیر نمایش داد:

$$\large { - y = \ln \left ( { \frac { { { x ^ 2 } } } { 2 } + C } \right )\;\;}\kern-0.3pt {\Rightarrow\;\;}\kern0pt { y = – \ln \left ( { \frac { { { x ^ 2 } } } { 2 } + C } \right ) . }$$

در عبارت اخیر فرض می‌کنیم برای آنکه دامنه لگاریتم صحیح باشد، $$C \gt 0$$ است.

مثال ۴

جواب خصوصی معادله دیفرانسیل $$\large x \left ( { y + 2 } \right ) y ’ = \ln x + 1$$ را برای $$y\left( 1 \right) = – 1$$ به‌دست آورید.

حل: با تقسیم هردو سمت معادله بر $$x$$، داریم:

$$\large { x \left ( { y + 2 } \right ) \frac { { d y } } { { d x } } = \ln x + 1 , \;\;} \Rightarrow { \left ( { y + 2 } \right ) d y = \frac { { \left ( { \ln x + 1 } \right ) d x } } { x } . }$$

فرض می‌کنیم $$x \ne 0$$ باشد،‌ زیرا دامنه معادله $$x>0$$ است.

حاصل انتگرال‌گیری از معادله به‌صورت زیر است:

$$\large { \int { \left ( { y + 2 } \right ) d y } } = { \int { \frac { { \left ( { \ln x + 1 } \right ) d x } } { x } } } + { C . }$$

انتگرال سمت راست به‌صورت زیر محاسبه می‌شود:

$$\large { \int { \frac { { \left ( { \ln x + 1 } \right ) d x } } { x } } } = { \int { \left ( { \ln x + 1 } \right ) d \left ( { \ln x } \right ) } } \\ \large = { \int { \left ( { \ln x + 1 } \right ) d \left ( { \ln x + 1 } \right ) } } = { \frac { { { { \left ( { \ln x + 1 } \right ) } ^ 2 } } } { 2 } . }$$

بنابراین، جواب عمومی به‌فرم ضمنی زیر خواهد بود:

$$\large { { { \frac{y ^ 2}{2} } + 2 y } = { \frac { { { { \left ( { \ln x + 1 } \right ) } ^ 2 } } } { 2 } } + { C , \;\; } } \Rightarrow { { { y ^ 2 } + 4 y } = { { \left ( { \ln x + 1 } \right ) ^ 2 } } + { { C _ 1 } , } }$$

که در آن $${C_1} = 2C$$ یک ثابت انتگرال‌گیری است. در ادامه، مقدار $$C_1$$ را محاسبه می‌کنیم که در شرایط اولیه $$y(1)=-1$$ صدق می‌کند:

$$\large { { { \left ( { – 1 } \right ) ^ 2 } + 4 \left ( { – 1 } \right ) } = { { \left ( { \ln 1 + 1 } \right ) ^ 2 } + { C _ 1 } , \;\; } } \Rightarrow { { C _ 1 } = – 4 . }$$

بنابراین، جواب خصوصی که شرایط اولیه در آن صدق می‌کند، برابر است با:

$$\large  { y ^ 2 } + 4 y = { \left ( { \ln x + 1 } \right ) ^ 2 } – 4 .$$

مثال ۵

جواب معادله دیفرانسیل $$y ^\prime { \cot ^ 2 } x + \tan y = 0$$ را به‌دست آورید.

حل: معادله را به‌صورت زیر می‌نویسیم:

$$\large { \frac { { d y } } { { d x } } { \cot ^ 2 } x = – \tan y , \;\;}\Rightarrow {{\cot ^2}xdy = – \tan ydx.}$$

دو سمت معادله را بر $$\tan y\,{\cot ^2}x$$ تقسیم می‌کنیم:

$$ \large \require { cancel }<br /> { { \frac { { \cancel { { \cot } ^ 2 } x d y } } { { \tan y \, \cancel { { \cot } ^ 2 } x } } } = { – \frac { { \cancel { \tan y } d x } } { { \cancel { \tan y } \, { { \cot } ^ 2 } x } } , \;\; } } \Rightarrow<br /> { \frac { { d y } } { { \tan y } } = – \frac { { d x } } { { { { \cot } ^ 2 } x } } . } $$

جواب‌های ازدست‌رفته ناشی از تقسیم را بررسی می‌کنیم که احتمالاً دو ریشه دارد:

$$\large \tan y \, { \cot ^ 2 } x = 0$$

ریشه اول از معادله زیر به‌دست می‌آید:

$$\large { \;\; \tan y = 0 , \;\; } \Rightarrow { y = \pi n, \; } \kern-0.3pt { n \in Z , \;} \kern -0.3pt { d y = 0 . }$$

با جایگذاری این ریشه در معادلات اولیه می‌بینیم که $$y = \pi n, \, n \in Z$$  یک جواب است.

دومین جواب، از معادله زیر به‌دست می‌آید:

$$\large { \cot ^ 2 } x = 0 .$$

و حل آن برابر است با:

$$\large { x =\frac{\pi}{2}+ \pi n , \;\; } \kern-0.3pt { n \in Z , \;\; } \kern-0.3pt { d x = 0 }$$

که در معادله دیفرانسیل اولیه صدق نمی‌کند.

اکنون می‌توانیم از معادله انتگرال بگیریم و جواب عمومی را به‌دست آوریم:

$$\large { { \int { \frac { { d y } } { { \tan y } } } } = { – \int { \frac { { d x } } { { { { \cot } ^ 2 } x } } } + C , \;\; } } \Rightarrow { { \int { \frac { { d y } } { { \frac { { \sin y } } { { \cos y } } } } } } = { – \int { \frac { { d x } } { { \frac { { { { \cos } ^ 2 } x } } { { { { \sin } ^ 2 } x } } } } } + C , \;\; } } \\ \large \Rightarrow { { \int { \frac { { \cos y d y } } { { \sin y } } } } = { – \int { \frac { { { { \sin } ^ 2 } x d x } } { { { { \cos } ^ 2 } x } } } + C , \;\; } } \Rightarrow { { \int { \frac { { d \left ( { \sin y } \right ) } } { { \sin y } } } } = { – \int { \frac { { 1 – { \cos ^ 2 } x } } { { { { \cos } ^ 2 } x } } d x } } + { C , \;\; } } \\ \large \Rightarrow { { \ln \left | { \sin y } \right | } = { – \int { \left ( { \frac { 1 }{ { { { \cos } ^ 2 } x } } – 1 } \right ) d x } } + { C , \;\; } } \\ \large \Rightarrow { { \ln \left | { \sin y } \right | } = { – \left ( { \tan x – x } \right ) + C , \;\; } } \Rightarrow { { \ln \left | { \sin y } \right | } = { – \tan x + x + C . } }$$

بنابراین، جواب نهایی معادله برابر است با:

 $$\large { { \ln \left | { \sin y } \right | + \tan x } - { x = C , \;\; } } \kern-0.3pt { { y = \pi n , \;\; } \kern-0.3pt { n \in Z . } }$$

مثال ۶

جواب خصوصی معادله دیفرانسیل $$\left( {1 + {e^x}} \right)y’ = {e^x}$$ را برای شرایط اولیه $$y\left( 0 \right) = 0$$ به‌دست آورید.

حل: معادله را به‌فرم زیر می‌نویسیم:

$$\large \left ( { 1 + { e ^ x } } \right ) d y = { e ^ x } d x .$$

با تقسیم آن بر $${1 + {e^x}}$$ داریم:

$$\large d y = \frac { { { e ^ x} } } { { 1 + { e ^ x } } } d x .$$

از آن‌جایی که $${1 + {e^x}} \gt 0$$ است،‌ جواب‌های معادله اصلی را از دست نمی‌دهیم. حاصل انتگرال‌گیری از این معادله، برابر است با:‌

$$\large { \int { d y } = \int { \frac { { { e ^ x } } } { { 1 + { e ^ x } } } d x } + C , \;\; } \Rightarrow { y = \int { \frac { { d \left ( { { e ^ x } } \right ) } } { { 1 + { e ^ x } } } } + C , \;\; }\\ \large \Rightarrow { y = \int { \frac { { d \left ( { { e ^ x } + 1 } \right ) } } { { 1 + { e ^ x } } } } + C , \;\; } \Rightarrow { y = \ln \left ( { { e ^ x } + 1 } \right ) + C . }$$

اکنون ثابت $$C$$ را از شرایط اولیه $$y(0) = 0$$ به‌دست می‌آوریم:

 $$\large { 0 = \ln \left ( { { e ^ 0 } + 1 } \right ) + C , \;\; } \Rightarrow { 0 = \ln 2 + C , \;\; } \Rightarrow { C = – \ln 2 . }$$

بنابراین، جواب نهایی معادله برابر است با:

$$\large { y = \ln \left ( { { e ^ x } + 1 } \right ) – \ln 2 } = { \ln \frac { { { e ^ x } + 1 } } { 2 } . }$$

مثال ۷

معادله دیفرانسیل $$y\left( {1 + xy} \right)dx =x\left( {1 – xy} \right)dy$$ را حل کنید.

حل: با ضرب عبارت $$xy$$ در دو سمت معادله، نمی‌توان متغیرها را جدا کرد. بنابراین، از تغییر متغیر زیر استفاده می‌کنیم:

$$\large xy = t\;\;$$   یا   $$\large y = \frac{t}{x}$$

بنابراین، رابطه دیفرانسیل‌ها به‌صورت زیر درخواهد آمد:

$$\large d y = \frac { { x d t – t d x } } { { { x ^ 2 } } } .$$

با جایگذاری رابطه اخیر در معادله داریم:

$$\large { \frac { t } { x } \left ( { 1 + t } \right ) d x } = { x \left ( { 1 – t } \right ) \frac { { x d t – t d x } } { { { x ^ 2 } } } . }$$

اکنون هردو طرف معادله را در $$x$$ ضرب می‌کنیم و خواهیم داشت:

$$\large { t \left ( { 1 + t } \right ) d x } = { \left ( { 1 – t } \right ) \left ( { x d t – t d x } \right ) . }$$

مقدار $$x = 0$$ یک جواب است که می‌توان آن را با جایگذاری مستقیم در معادله اثبات کرد.

معادله آخر را به‌صورت زیر ساده می‌کنیم:

$$\large { { t d x + \cancel { { t ^ 2 } d x } } = { x d t – t d x } -{ x t d t + \cancel { { t ^ 2 } d x } , \;\; } }\\ \large \Rightarrow { 2 t d t = x \left ( { 1 – t } \right ) d t . }$$

اکنون متغیرهای $$x$$ و $$t$$ جدا شده‌اند:

$$\large { \frac { { 2 d x } } { x } = \frac { { \left ( { 1 – t } \right ) d t } } { t } \;\;}$$

یا

$$\large { 2 \frac { { d x } } { x } = \left ( { \frac { 1 } { t } – 1 } \right ) d t . }$$

پس از انتگرال‌گیری داریم:

$$\large { { 2 \int { \frac { { d x } } { x } } } = { \int { \left ( { \frac { 1 } { t } – 1 } \right ) d t } + C , \;\; } }\\ \large \Rightarrow { { 2 \ln \left | x \right | } = { \ln \left | t \right | – t + C , \;\; } } \Rightarrow { { \ln { x ^ 2 } } = { \ln \left | t \right | – t + C . } }$$

مثال ۸

جواب عمومی معادله دیفرانسیل $$\left ( { x + y + 1 } \right ) d x + \left ( { 4 x + 4 y + 1 0 } \right ) d y = 0$$ را به‌دست آورید.

حل: از تغییر متغیر زیر استفاده می‌کنیم:

$$\large { x + y = u , \;\; } \Rightarrow { y = u – x , \;\; } \kern0pt { d y = d u – d x . }$$

با جایگذاری در معادله، داریم:

$$\large { \left ( { u + 1 } \right ) d x } + { \left ( { 4 u + 1 0 } \right ) \left ( { d u – d x } \right ) } = { 0 . }$$

بنابراین، خواهیم داشت:

$$\large { u d x + d x + 4 u d u } + { 1 0 d u } - { 4 u d x } - { 1 0 d x } = { 0 , } \\ \large { – 3 u d x – 9 d x + 4 u d u } + { 1 0 d u } = { 0 , } \\ \large { - 3 \left ( { u + 3 } \right ) d x + 2 \left ( { 2 u + 5 } \right ) d u } = { 0 , } \\ \large \frac { { 3 d x } } { 2 } = \frac { { 2 u + 5 } } { { u + 3 } } d u .$$

اکنون از معادله اخیر انتگرال می‌گیریم:

$$\large { { \frac { 3 } { 2 } \int { d x } } = { \int { \frac { { 2 u + 5 } } { { u + 3 } } d u } + C ,\;\; } } \Rightarrow { { \frac { 3 } { 2 }\int { d x } } = { \int { \frac { { 2 u + 6 – 1 } } { { u + 3 } } d u } + C , \;\; } } \\ \large \Rightarrow { { \frac { 3 } { 2 } \int { d x } } = { \int { \left ( { 2 – \frac { 1 } { { u + 3 } } } \right ) d u } + C , \; \; } } \Rightarrow { { \frac { 3 } { 2 } x } = { 2 u – \ln \left | { u + 3 } \right | + C . } }$$

از آن‌جایی که تساوی $$u = x + y$$ برقرار است، جواب نهایی را می‌توان به‌فرم ضمنی زیر نوشت:

$$\large { { \frac { 3 } { 2 } x = 2 \left ( { x + y } \right ) } - { \ln \left | { x + y + 3 } \right | } + { C \; \; } }$$

یا

$$\large \frac { x } { 2 } + 2 y - { \ln \left | { x + y + 3 } \right | } + { C = 0 . }$$