معادله دیفرانسیل اویلر – به زبان ساده (+ دانلود فیلم آموزش رایگان)

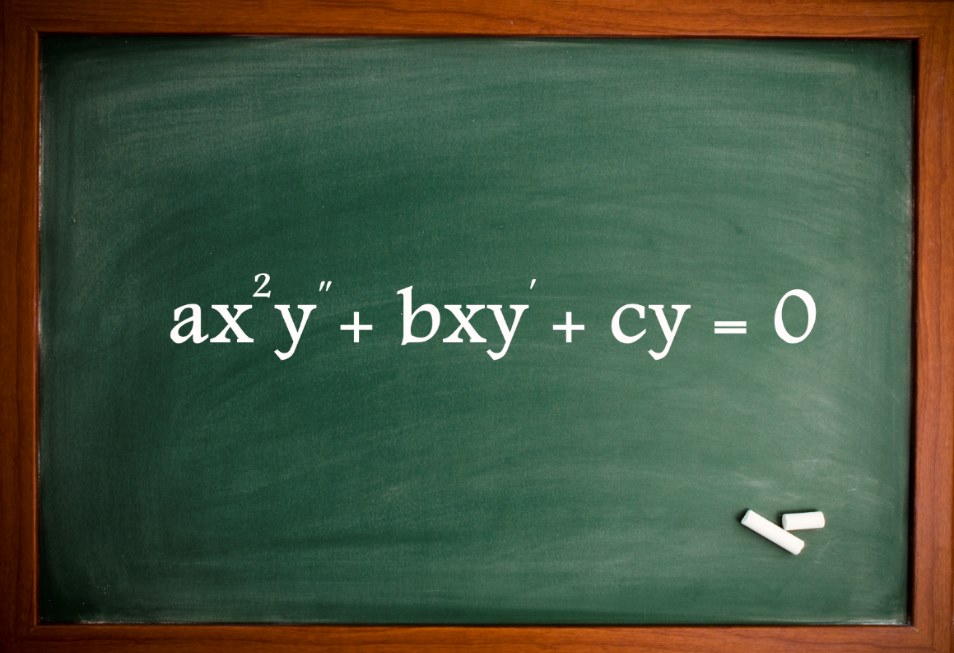
در راستای ارائه مفاهیم مرتبط با معادلات دیفرانسیل، روش‌های حل این معادلات اعم از مرتبه اول، دوم و مراتب بالاتر توضیح داده ‌شدند. با این حال در این مطلب قصد داریم تا نوعی جدید از معادلات دیفرانسیل، تحت عنوان معادله دیفرانسیل اویلر را مورد بررسی قرار دهیم. از این رو پیشنهاد می‌شود قبل از مطالعه این بخش، مطالب معادلات دیفرانسیل، مرتبه دوم، معادلات دیفرانسیل مرتبه بالاتر و معادلات ناهمگن را مطالعه فرمایید.

شکل معادله دیفرانسیل اویلر

معادله دیفرانسیل اویلر به معادله‌ای از مرتبه دو گفته می‌شود که در آن درجه ضرایبِ تابع و مشتقاتش برابر با مرتبه مشتق‌گیری است. در حقیقت شکل عمومی یک معادله دیفرانسیل اویلر به صورت زیر است.

$$\large \begin {equation} a { x ^ 2 } y ^ { \prime\prime } + b x y ^ { \prime } + c y = 0 \end {equation}$$

پاسخ معادله دیفرانسیل اویلر را می‌توان به دو صورت بیان کرد. حالت اول را به صورت سری توانی بیان می‌کنند. اما در این مطلب، هدف ما بدست آوردن پاسخ تحلیلی این معادله است.
در ابتدا فرض کنید مقادیر x مثبت هستند ($$x > 0$$). در ادامه و در مثال ۱، علت این فرض را توضیح خواهیم داد. البته این معادله در تمامی xها به جز x=0 دارای پاسخ است. بنابراین شکل عمومی پاسخ را در انتها ارائه خواهیم داد. اویلر نشان دادن که پاسخ چنین معادله‌ای را می‌توان به صورت زیر در نظر گرفت.

$$\large \begin {equation} y \left ( x \right ) = { x ^ r } \end {equation}$$
رابطه ۱

با قرار دادن پاسخ فرض شده در معادله اصلی، داریم:

$$\large \begin {align*} a { x ^ 2 } \left ( r \right ) \left ( { r - 1 } \right ) { x ^ { r - 2 } } + b x \left ( r \right ) { x ^ { r - 1 } } + c { x ^ r } & = 0 \\ a r \left ( { r - 1 } \right ) { x ^ r } + b \left ( r \right ) { x ^ r } + c { x ^ r } & = 0 \\ \left ( { a r \left ( { r - 1 } \right ) + b \left ( r \right ) + c } \right ) { x ^ r } & = 0 \end {align*}$$

با ساده کردن عبارت فوق و فرض x>0، عبارت زیر بدست می‌آید.

$$\large \begin {equation} a r \left ( { r - 1 } \right ) + b \left ( r \right ) + c = 0 \end {equation}$$
رابطه ۲

بنابراین با فرض رابطه ۱ به عنوان پاسخ معادله، به رابطه ۲ به عنوان یک معادله مشخصه می‌رسیم. رابطه ۲، معادله‌ای درجه ۲ را نشان می‌دهد. بنابراین سه حالت می‌تواند برای پاسخ‌های این معادله درجه ۲ وجود داشته باشد.

1. پاسخ‌های حقیقی متفاوت
2. پاسخ‌های مختلط
3. پاسخ‌ مضاعف (یا همان پاسخ تکراری)

شکل پاسخ نهایی معادله دیفرانسیل اویلر در هریک از حالات فوق، متفاوت خواهد بود. در ادامه پاسخ یک معادله دیفرانسیل اویلر در هریک از حالات مذکور توضیح داده شده است.

حالت اول: پاسخ‌های حقیقی متفاوت

در این حالت پاسخ پیچیده نخواهد بود. همان‌طور که در مطلب معادلات دیفرانسیل مرتبه دوم نیز عنوان شد، اگر y₁ و y₂ پاسخ‌هایی از یک معادله دیفرانسیل خطی باشند. در این صورت ترکیب خطی آن‌ها را می‌توان به عنوان پاسخ عمومی معادله در نظر گرفت. معادله دیفرانسیل اویلر نیز از این قاعده مستثنی نیست.

فیلم آموزش معادلات دیفرانسیل + حل سوالات کنکور کارشناسی ارشد در فرادرس

کلیک کنید

بنابراین فرض کنید پاسخ رابطه ۲، دو عدد حقیقی و متفاوت r₁ و r₂ باشند. در این صورت پاسخ‌های y₁ و y₂ برابرند با:

$$\large y _ 1 = x ^ { r _ 1 } \ \ , \ \ y _ 2 = x ^ { r _ 2 }$$

بنابراین پاسخ عمومی معادله دیفرانسیل اویلر در این حالت برابر است با:

$$\large \boxed { y \left ( x \right ) = { c _ 1 } { x ^ { { r _ 1 } } } + { c _ 2 } { x ^ { { r _ 2 } } } }$$

در ادامه مثال‌هایی ذکر شده که این حالات در آن‌ها بررسی شده‌اند.

مثال ۱

پاسخ معادله مقدار اولیه زیر را در بازه x>0 بیابید.

$$\large 2 { x ^ 2 } y ^ { \prime \prime } + 3 x y ^ { \prime } - 1 5 y = 0 \ , \hspace {0.25in} \ \ y \left ( 1 \right ) = 0 \ \ \ , \, \, \, \, y ^ { \prime } \left ( 1 \right ) = 1$$

در ابتدا لازم است رابطه ۲ را برای معادله فوق تشکیل دهیم. در معادله مذکور $$a = 2 , b = 3 , c = - 15$$ هستند. بنابراین معادله مشخصه این معادله به صورت زیر بدست می‌آید.

$$\large \begin {align*} 2 r \left ( { r - 1 } \right ) + 3 r - 1 5 & = 0 \\ 2 { r ^ 2 } + r - 1 5 = \left ( { 2 r - 5 } \right ) \left ( { r + 3 } \right ) & = 0 \hspace {0.25in} \Rightarrow \hspace {0.25in} { r _ 1 } = \frac { 5 } { 2 } , \, \, \, { r _ 2 } = - 3 \end {align*}$$

همان‌طور که در بالا نیز محاسبه شد، پاسخ‌های معادله مشخصه دو عدد حقیقیِ متفاوت هستند؛ لذا پاسخ نهایی معادله به صورت زیر در نظر گرفته می‌شود.

$$\large y \left ( x \right ) = { c _ 1 } { x ^ { \frac { 5 } { 2 } } } + { c _ 2 } { x ^ { - 3 } }$$

به منظور یافتن ثابت‌های c₁ و c₂ باید $$\large y ^ { \prime }$$ محاسبه شود.

$$\large y ^ { \prime } \left ( x \right ) = \frac { 5 } { 2 } { c _ 1 } { x ^ { \frac { 3 } { 2 } } } - 3 { c _ 2 } { x ^ { - 4 } }$$

با اعمال شرایط مرزی روی y و 'y داریم:

$$\large \left. \begin {align*} & 0 = y \left ( 1 \right ) = { c _ 1 } + { c _ 2 } \\ & 1 = y ^ { \prime } \left ( 1 \right ) = \frac { 5 } { 2 } { c _ 1 } - 3 { c _ 2 } \end {align*} \right \} \hspace {0.25in} \Rightarrow \hspace{0.25in} { c _ 1 } = \frac { 2 } { { 1 1 } } , \, \, { c _ 2 } = - \frac { 2 } { { 1 1 } }$$

با بدست آمدن ضرایب ثابت، پاسخ نهایی نیز به صورت زیر محاسبه می‌شود.

$$\large y \left ( x \right ) = \frac { 2 } { { 1 1 } } { x ^ { \frac { 5 } { 2 } } } - \frac { 2 } { { 1 1 } } { x ^ { - 3 } }$$

حال که مثال ۱ حل شده، دلیل مثبت فرض شدن x معلوم می‌شود. با دقت در پاسخ بدست آمده می‌بینید که اگر x=0 باشد، ترم اول بی‌معنی شده در صورت استفاده از xهای منفی، عبارت دوم قابل محاسبه نیست.

حالت دوم: ریشه مضاعف یا ریشه تکراری

در این حالت هر دو ریشه رابطه ۱، عددی حقیقی و یکسان هستند. فرض کنید ریشه‌ها به صورت زیر باشند.

$$\large \ r_ { 1 , 2 } \ = r$$

فیلم آموزش معادلات دیفرانسیل با میپل Maple در فرادرس

کلیک کنید

می‌توان نشان داد که در این حالت پاسخ عمومی معادله به صورت زیر خواهد بود.

$$\large y \left ( x \right ) = { c _ 1 } { x ^ r } + { c _ 2 } { x ^ r } \ln x = { x ^ r } \left ( { { c _ 1 } + { c _ 2 } \ln x } \right )$$

در این حالت نیز می‌بینید که با توجه به موجود بودن لگاریتم در پاسخ، مقادیر x باید مثبت باشند.

مثال ۲

پاسخ عمومی معادله زیر را در بازه x>0 بیابید.

$$\large { x ^ 2 } y ^ { \prime \prime } - 7 x y { \prime } + 1 6 y = 0$$

با توجه به مقادیر b ،a و c معادله مشخصه به صورت زیر قابل نوشتن است.

$$\large \begin {align*} r \left ( { r - 1 } \right ) - 7 r + 1 6 & = 0 \\ { r ^ 2 } - 8 r + 1 6 & = 0 \\ { \left ( { r - 4 } \right ) ^ 2 } & = 0 \hspace {0.25in} \Rightarrow \hspace {0.25in} r _ { 1 , 2 } = 4 \end {align*}$$

همان‌طور که می‌بینید، جواب‌های معادله مشخصه به صورت مضاعف هستند. بنابراین پاسخ عمومی معادله دیفرانسیل اویلر به صورت زیر بدست می‌آید.

$$\large y \left ( x \right ) = { c _ 1 } { x ^ 4 } + { c _ 2 } { x ^ 4 } \ln x$$

اگر دوست‌دار ریاضیات هستید، احتمالا بخش بعدی جذاب‌ترین بخش این مطلب برای شما باشد.

حالت سوم: ریشه‌های مختلط

در این حالت پاسخ‌های رابطه ۲ به صورت مختلط بوده و به شکل زیر در نظر گرفته می‌شوند:

$$\large { r _ { 1 , 2 } } = \lambda \pm \mu \, i$$

بنابراین یکی از پاسخ‌ها به شکل زیر است.

$$\large y \ = \ { x ^ { \lambda + \mu \, i } }$$

توجه داشته باشید که پاسخ معادله دیفرانسیل نمی‌تواند مختلط باشد (برای نمونه x نشان دهنده پارامتری فیزیکی است که نمی‌تواند مختلط باشد). از این رو x^r را با استفاده از قوانین لگاریتم به صورت زیر بازنویسی می‌کنیم.

$$\large { x ^ r } = { { \bf { e } } ^ { \ln { x ^ r } } } = { { \bf { e } } ^ { r \ln x } }$$

با جایگذاری r در پاسخ در نظر گرفته شده، داریم:

$$\large \begin {align*} { x ^ { \lambda + \mu \, i } } & = { { \bf { e } } ^ { \left ( { \lambda + \mu \,i} \right ) \ln x } } \\ & = { { \bf { e } } ^ { \lambda \ln x } } { { \bf { e } } ^ { \mu \, i \ln x} } \\ & = { { \bf { e } } ^ { \ln { x ^ \lambda } } } \left ( { \cos \left ( { \mu \ln x } \right ) + i \sin \left ( { \mu \ln x } \right ) } \right ) \\ & = { x ^ \lambda } \cos \left ( { \mu \ln x } \right ) + i { x ^ \lambda } \sin \left ( { \mu \ln x } \right ) \end {align*}$$

با انجام همین کار برای $$y \ = \ { x ^ { \lambda - \mu \, i } }$$ به پاسخی خواهیم رسید که قرینه بخش موهومی پاسخ بالا است. نهایتا ترکیب خطی دو پاسخ بدست آمده به صورت زیر خواهد بود.

$$\large y \left ( x \right ) = { c _ 1 } { x ^ \lambda } \cos \left ( { \mu \ln x } \right ) + { c _ 2 }{ x ^ \lambda } \sin \left ( { \mu \ln x } \right ) = { x ^ \lambda } \left ( { { c _ 1 } \cos \left ( { \mu \ln x } \right ) + { c _ 2 } \sin \left ( { \mu \ln x } \right ) } \right )$$

در این حالت می‌بینید که در پاسخ، عبارت لگاریتمی وجود دارد. بنابراین مقدار x در این حالت نیز باید مثبت باشد (x>0).

فیلم رابطه اویلر در اعداد مختلط + بررسی دموآور و حل مثال (فیلم آموزش رایگان) در فرادرس

کلیک کنید

مثال 3

پاسخ معادله دیفرانسیل زیر را در بازه x>0 بیابید.

$$\large { x ^ 2 } y ^ { \prime\prime } + 3 x y ^ { \prime } + 4 y = 0$$

معادله مشخصه برای این معادله دیفرانسیل اویلر به صورت زیر است.

$$\large \begin {align*} r \left ( { r - 1 } \right ) + 3 r + 4 & = 0 \\ { r ^ 2 } + 2 r + 4 & = 0 \hspace {0.25in} \Rightarrow \hspace {0.25in} { r _ { 1 , 2 } } = - 1 \pm \sqrt 3 \, i \end {align*}$$

پاسخ‌های بدست آمده به صورت مختلط هستند. بنابراین پاسخ عمومی معادله به صورت زیر بدست می‌آید.

$$\large y \left ( x \right ) = { c _ 1 } { x ^ { - 1 } } \cos \left ( { \sqrt 3 \ln x } \right ) + { c _ 2 } { x ^ { - 1 } } \sin \left ( { \sqrt 3 \ln x } \right )$$

توجه داشته باشید که واقعیت این است که معادله در تمامی بازه‌ها دارای پاسخ است. در واقع x می‌تواند هر عددی به جز صفر باشد. با جایگذاری |x| به جای x پاسخ کلی معادله اویلر بدست می‌آید. برای نمونه پاسخ معادله دیفرانسیل اویلر در حالتی که ریشه‌های معادله مشخصه دو عدد حقیقی متفاوت باشند، به‌ صورت زیر است.

$$\large y \left ( x \right ) = { c _ 1 } { \left | x \right | ^ { { r _ 1 } } } + { c _ 2 } { \left | x \right | ^ { { r _ 2 } } } ,\hspace{0.25in} x \ne 0$$

به همین صورت در حالت ریشه مضاعف و پاسخ مختلط نیز پاسخ‌ها به ترتیب برابرند با:

$$\large \begin {align*} y \left ( x \right ) & = { c _ 1 } { \left | x \right | ^ r } + { c _ 2 } { \left | x \right | ^ r } \ln \left | x \right | \\ y \left ( x \right ) & = { c _ 1 } { \left | x \right | ^ \lambda } \cos \left ( { \mu \ln \left | x \right | } \right ) + { c _ 2 } { \left | x \right | ^ \lambda } \sin \left ( { \mu \ln \left | x \right | } \right ) \end {align*}$$

توجه داشته باشید که در برخی موارد با معادله‌ای به شکل زیر مواجه خواهید بود. چنین معادله‌ای نیز از نوع اویلر است.

$$\large a { \left ( { x - { x _ 0 } } \right ) ^ 2 } y ^ { \prime \prime } + b \left ( { x - { x _ 0 } } \right ) y ^ { \prime } + c y = 0$$

در این حالت معادله در تمامی‌ xها به جز x=x₀ دارای پاسخ است. پاسخ‌ها نیز در هریک از حالات به صورت زیر هستند.

$$\large \begin {align*} y \left ( x \right ) & = { c _ 1 } { \left | { x - a } \right | ^ { { r _ 1 } } } + { c _ 2 } { \left | { x - a } \right | ^ { { r _ 2 } } } \\ y \left ( x \right ) & = { \left| {x - a} \right| ^ r } \left ( { { c _ 1 } + { c _ 2 } \ln \left | { x - a } \right | } \right ) \\ y \left ( x \right ) & = {\left| {x - a} \right|^\lambda }\left( {{c_1}\cos \left( {\mu \ln \left| {x - a} \right|} \right) + { c _ 2 } \sin \left( {\mu \ln \left| { x - a } \right | } \right ) } \right ) \end {align*}$$

در روابط بالا مقادیر r، ریشه‌های معادله زیر هستند (دقیقا مشابه با حالت قبل).

$$\large a r \left ( { r - 1 } \right ) + b \left ( r \right ) + c = 0$$

مثال ۴

پاسخ معادله دیفرانسیل زیر را بیابید.

$$\large 3 { \left ( { x + 6 } \right ) ^ 2 } y ^ { \prime\prime } + 2 5 \left ( { x + 6 } \right ) y ^ { \prime } - 1 6 y = 0$$

با توجه به معادله فوق، معادله مشخصه و ریشه‌های مرتبط با آن به صورت زیر بدست می‌آیند.

$$\large \begin {align*} 3 r \left ( { r - 1 } \right ) + 2 5 r - 1 6 & = 0 \\ 3 { r ^ 2 } + 2 2 r - 16 & = 0 \\ \left ( { 3 r - 2 } \right ) \left ( { r + 8 } \right ) & = 0 \hspace {0.25in} \Rightarrow \hspace {0.25in} { r _ 1 } = \frac { 2 } { 3 } ,\, \, { r _ 2 } = - 8 \end {align*}$$

ریشه‌های معادله مشخصه حقیقی‌اند؛ بنابراین پاسخ معادله به صورت زیر بدست می‌آید.

$$\large y \left ( x \right ) = { c _ 1 } { \left| { x + 6 } \right| ^ { \frac { 2 } { 3 } } } + { c _ 2 } { \left | { x + 6 } \right | ^ { - 8 } }$$

در این مطلب شکل کلی یک معادله دیفرانسیل اویلر و نحوه بدست آوردن پاسخ آن در سه حالت مختلف توضیح داده شد. در ابتدا پاسخ‌ها در حالتِ x>0 مورد بررسی قرار گرفتند. در انتهای مطلب نیز پاسخ کلی معادله در هریک از حالات، در تمامی مقادیر مثبت و منفی x، ارائه شد.