معادلات دیفرانسیل ناهمگن مرتبه دوم با ضرایب متغیر — از صفر تا صد
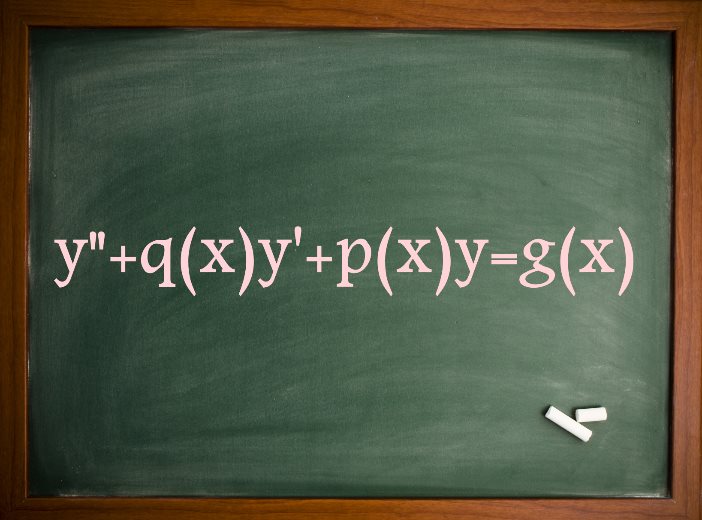
در مطالب گذشته وبلاگ فرادرس در مورد مفاهیم معادلات دیفرانسیل و همچنین معادلات دیفرانسیل ناهمگن مرتبه دوم صحبت کردیم. از این رو در این مطلب قصد داریم تا نوع خاصی از معادلات دیفرانسیل، تحت عنوان معادلات دیفرانسیل مرتبه دوم ناهمگن با ضرایب متغیر را معرفی کرده و نحوه حل آن را نیز توضیح دهیم. توجه داشته باشید که قبل از مطالعه این مطلب لازم است تا مطلب معادلات دیفرانسیل مرتبه دوم با ضرایب متغیر را مطالعه فرمایید.
معادلات دیفرانسیل ناهمگن با ضرایب متغیر
یک معادله دیفرانسیل ناهمگن مرتبه دوم با ضرایب متغیر به صورت زیر است.
$$ \large { y ^ { \prime \prime } + { a _ 1 } \left ( x \right ) y ^ { \prime } } + { { a _ 2 } \left ( x \right ) y } = { f \left ( x \right ) } $$
توجه داشته باشید که $$a_1(x)$$ و $$a_2(x)$$، توابعی پیوسته در بازه $$[a,b]$$ هستند. همچنین معادله همگن مرتبط با معادله فوق، برابر است با:
$$ \large { y ^ { \prime \prime } + { a _ 1 } \left ( x \right ) y ^ { \prime } } + { { a _ 2 } \left ( x \right ) y } = { 0 } $$
پاسخ عمومی معادله ناهمگن برابر با پاسخ عمومی معادله همگن مرتبط یا همان $$y_0(x)$$ به همراه پاسخ خصوصی $$Y(x)$$ در نظر گرفته میشود. در نتیجه پاسخ عمومی یک معادله ناهمگن برابر است با:
$$ \large y \left ( x \right ) = { y _ 0 } \left ( x \right ) + Y \left ( x \right ) $$
به منظور بدست آوردن پاسخ عمومی معادله ناهمگن، استفاده از روشهای زیر نیز میتوانند مفید باشد.
- حدس زدن پاسخ خصوصی معادله ناهمگن با استفاده از شکل ترم ناهمگن
- استفاده از فرمول لیوویل و بدست آوردن پاسخ عمومی معادله همگن
- استفاده از روش تغییر متغیرها به منظور بدست آوردن پاسخ عمومی معادله همگن
قبلا در مورد روش تغییر پارامترها صحبت کرده بودیم. با این حال در ادامه به طور اختصاصی این روش را توضیح داده و مثالهایی را از آن ارائه خواهیم داد.
روش تغییر پارامترها
فرض کنید هدف ما حل یک معادله مرتبه دوم ناهمگن است. با فرض اینکه پاسخهای پایه معادله برابر با $$y_1(x)$$ و $$y_2(x)$$ باشند، در این صورت پاسخ عمومی معادله همگن را میتوان به صورت زیر در نظر گرفت.
$$ \large { { y _ 0 } \left ( x \right ) } = { { C _ 1 } { y _ 1 } \left ( x \right ) + { C _ 2 }{ y _ 2 } \left ( x \right ) } $$
حال به جای استفاده از $$ C _ 1 $$ و $$ C _ 2 $$ ضرایب را برابر با $$ C _ 1 ( x ) $$ و $$ C _ 2 ( x ) $$ در نظر گرفته و پاسخ عمومی معادله ناهمگن را برابر با تابع زیر در نظر میگیریم.
$$ \large {y = { C _1 } \left ( x \right ) { Y _ 1 } \left ( x \right ) } + { { C _ 2 } \left( x \right){ Y _ 2 } \left ( x \right ) } $$
در حقیقت با جایگذاری پاسخ فوق در معادله اصلی این ضرایب بدست خواهند آمد. توجه داشته باشید که پاسخ در نظر گرفته شده در هر دو معادله همگن و ناهمگن صدق میکنند. بنابراین به منظور یافتن ضرایب متغیرِ $$ C _ 1 ( x ) $$ و $$ C _ 2 ( x ) $$، باید دستگاه معادلات زیر حل شوند.
$$ \large \left\{ \begin{array}{l}
{ C^{\prime} _ 1(x) } { y_1(x) } + { C ^ {\prime } _ 2(x) } y_2(x) = 0 \\~\\
{ { C^{\prime} _ 1(x)}{y_1^{\prime}(x) } + { C ^ { \prime} _ 2 ( x ) } { y_2^{\prime}(x) }} = {f(x) {\large }}
\end{array} \right. $$
دترمینان سیستم معادلات فوق تحت عنوان رونسکین دو تابع $$y _ 1 $$ و $$y _ 2 $$ شناخته میشود. باید بدانید که رونسکین دو تابع مستقل خطی، مخالف صفر است. از این رو چنین سیستمی همواره دارای پاسخ خواهد بود. نهایتا رابطهای که با استفاده از آن ضرایب محاسبه میشوند، برابر است با:
$$\large { { C ^ { \prime } _ 1 } \left ( x \right ) = – \frac { {{y _ 2 } \left ( x \right ) f \left ( x \right ) }} { { { W_ {{ y _ 1 } , { y _ 2} } } \left ( x \right ) } } \ ,\;\;} \kern-0.3pt
{ { C ^ { \prime } _ 2 } \left( x \right) = \frac { { { y_ 1 } \left( x \right)f\left( x \right ) }}{{ { W _{ { y _ 1 } , { y _ 2} } } \left( x \right ) } } } $$
توجه داشته باشید که $$f(x)$$ نشاندهنده تابع در حالتی است که معادله به صورت استاندارد نوشته شده باشد. در حقیقت حالت استاندارد زمانی است که ضریبِ مشتق دومِ تابع یا همان $$a_0(x)$$ برابر با $$۱$$ باشد. با استفاده از روابط فوق مشتقات ضرایب بدست آمدند. بنابراین ضرایبِ $$ C _ 1 ( x ) $$ و $$ C _ 2 ( x ) $$ برابرند با:
$$\large { { {C _ 1 }\left( x \right) }={ – {\Large {\int}} {\frac{{{y_2}\left( x \right)f\left( x \right)}}{ { { W _ { { y _1 } , { y _ 2 }} }\left( x \right)}}dx} }+{ { A _1 } } }\kern-0.3pt \\~\\ \large{ { { C
_2}\left( x \right) }={ {\Large {\int}} {\frac { {{ y _1 }\left( x \right)f\left( x \right ) } } { { {W _ { { y_ 1 }{ y _ 2} } }\left( x \right ) } }d x } }+{ {A _ 2} } } $$
در دو رابطه فوق ضرایب $$A$$ ثابت هستند. بنابراین نهایتا پاسخ معادله دیفرانسیل ناهمگن با ضرایب متغیر مطابق با رابطه زیر بدست خواهند آمد.
$$\ \ \ \ \ \ \ \large \begin {align*} { y \left( x \right) } & = { {C_1}\left( x \right){y_1}\left( x \right) + {C_2}\left( x \right ) { y _2 } \left( x \right) } \\\\ & = { { \left [ { – \int { \frac { { {y _ 2 } \left( x \right)f\left( x \right ) } }{ {
{ W _ { { y_ 1 } , { y _ 2} } } \left( x \right ) } } dx } + {A_1}} \right] \cdot}\kern0pt{ {y_1} \left ( x \right) }}
+ { { \left[ {\int {\frac { { { y _1 } \left( x \right)f\left( x \right ) } }{ { {W _ { {y _1 } ,{ y _2 } } } \left ( x \right ) } } d x } + { A _ 2 } } \right] \cdot} \kern0pt { { y _ 2 } \left( x \right) } } \\\\ & = { { { A_ 1 } {y _ 1} \left( x \right) + { A _2 } { y _2 } \left( x \right) } + { Y \left( x \right) } } \end {align*} $$
در رابطه بالا $$ Y ( x ) $$ نشان دهنده پاسخ خصوصی معادله بوده و مطابق با رابطه زیر بدست میآید.
$$ \large { Y \left( x \right) }
= { { y _ 2 } \left ( x \right)\int {\frac { {{ y _1 }\left( x \right)f\left ( x \right ) } }{ {{ W _{ { y _ 1 } ,{ y _ 2 } } }\left ( x \right ) }} d x } }
– { { y _ 1 }\left ( x \right ) \int {\frac { { {y _ 2 }\left( x \right)f\left( x \right)}}{{{W_{{y_1},{y _ 2 }} }\left( x \right)}}dx} }$$
در ادامه مثالهایی ارائه شده که پیشنهاد میشود آن را مطالعه فرمایید.
مثال ۱
پاسخ خصوصی معادله دیفرانسیل زیر را برای $$x$$های مثبت بدست آورید.
$$ \large { x ^2 } y ^ { \prime\prime} – 2 x y ^{\prime } + 2 y = x^2+1 $$
در ابتدا معادله دیفرانسیل همگنِ مرتبط را به صورت زیر بیان میکنیم.
$$ \large { x ^2 } y ^ { \prime\prime} – 2 x y ^{\prime } + 2 y =0 $$
در مرحله بعد باید با استفاده از روشهای حل معادلات دیفرانسیل همگن، یکی از پاسخهای معادله همگن را یافت. بنابراین یکی از این پاسخها برابر است با:
$$\large y _ 1 = x $$
با تعیین شدن $$y_1$$ میتوان با استفاده از مفهوم رونسکین، پاسخ دوم که نسبت به $$y_1$$ نیز مستقل خطی است را پیدا کرد.
$$ \large { { W _ {{ y _1 } {y _2 } } }\left( x \right) = \left| {\begin{array}{*{20}{c}}
{ {y_1 } } & {{ y _ 2} }\\
{ { y ^ { \prime } _ 1 } } & { { y ^ { \prime } _ 2 } }
\end{array}} \right| }
= { { C_ 1 } \exp \left( { – \int {\frac { { { a _ 1 } \left( x \right ) }} { {{ a _2 } \left( x \right)}}dx} } \right) } $$
عبارت فوق به صورت زیر ساده میشود.
$$ \large \begin {align*} { y ^{\prime} _ 2 } { y _ 1 } – { y _ 2 } { y ^{\prime} _ 1 } & = {{C_1}{e^{ – \int {\left ( { \large \frac { { – 2 x } }{ { { x ^2 } }} \normalsize} \right ) d x } } } } \\\\ & = { {C _1 } {e ^ { 2 \int { \large \frac { { dx } } {x }\normalsize} } } } = { { C _1 }{ e ^ { 2 \ln \left| x \right|}} } \\\\ & = { { C _ 1 } {e ^ { \ln { x ^ 2 } } } } = { { C_1 } { x ^2 } } \end {align*} $$
با تقسیم کردن آن به $$y_1^2$$ میتوان عبارت فوق را به صورت زیر بازنویسی کرد.
$$ \large \begin {align*} \frac { { { y ^{\prime} _ 2 }{ y_1} – { y _ 2 } { y ^ { \prime } _ 1 } }} {{y_1^ 2 } } & = { \frac { { { C _ 1 } { x ^2 } } }{ { y_ 1 ^ 2 }} } \\ & = { \frac { { {C _ 1 } { x ^ 2 } } }{ { {x ^ 2 }}} = {C_1} \;\;} \\ & \ \ \Rightarrow { { \left( {\frac { { {y _2 } }} { { { y_ 1 } } } } \right)^\prime } = {C_1} } \end {align*} $$
نهایتا تابع مستقلِ $$y_2$$ برابر است با:
$$ \large \begin {align*} \frac { { {y _ 2 } }} { { {y_1}}} & = { C _1 } x + {C_2} \
\\\\ & \Rightarrow { { y _ 2} = { y _ 1} \left( { { C_ 1 } x + {C_2}} \right) } \\\\ & = { x\left( {{C_1}x + {C_2}} \right) }={ { C _ 1 }{ x ^ 2} + {C_2}x } \end {align*} $$
بنابراین پاسخ عمومی معادله همگن برابر است با:
$$ \large { y_ 0 } \left ( x \right ) = { C _1 } { x ^ 2 } + { C _ 2} x$$
حال با استفاده از روش تغییر پارامترها میخواهیم پاسخ معادله ناهمگن را بیابیم. بدین منظور ضرایب $$C_1 (x) $$ و $$C_2 (x)$$ را در نظر گرفته و پاسخ معادله ناهمگن را به صورت زیر در نظر میگیریم.
$$ \large { y } \left ( x \right ) = { C _1 (x) } { x ^ 2 } + { C _ 2(x)} x$$
با جایگذاری پاسخ در نظر گرفته شده در معادله همگن و ناهمگن، دستگاه معادلات به منظور یافتن ضرایب به صورت زیر بدست خواهند آمد.
$$\large \left\{ \begin{array}{l}
{ C^{\prime} _ 1 } { x ^ 2 } + { C ^ {\prime } _ 2 } x = 0 \\~\\
{ { C ^{\prime} _ 1}{\left( {{x^2}} \right)^\prime } + { C ^ { \prime} _ 2 } { \left( x \right)^\prime }} = {{1 + {\Large \frac { 1 } {{ { x ^ 2 } } } } }}
\end{array} \right.$$
همانطور که میبینید سمتِ راستِ معادله به نحوی نوشته شده که ضریب مشتق دوم برابر با $$1$$ است. در ادامه نحوه بدست آوردن شکل استاندارد $$f(x)$$ نشان داده شده است.
$$\large \begin {gather*} {x ^ 2 }y ^ { \prime \prime } – 2 x y ^ { \prime} + 2 y = { { x ^ 2 } + 1} \\\\ \Rightarrow y^{\prime\prime} – \frac {2 }{ x } y ^{\prime} + \frac { 2 } {{ { x ^ 2 } } } y ={ 1 + \frac{1}{{ { x^ 2 } } } } \end {gather*} $$
در مرحله بعد ضرایب $$ C(x) $$ با روند زیر بدست خواهند آمد.
$$\large \begin {align*} { C ^{\prime}_1} & = \frac{1}{x} + \frac{1} { { { x ^ 3} }} \kern-0.3pt \ \ , \ \ {C^{\prime} _ 2 } = – 1 – \frac { 1 }{ { {x ^ 2 }} } \\\\ & \Rightarrow {{C_1} = \ln x – \frac{1}{{ 2 { x ^2 } }} + {A_1} \ , \;\;}\kern-0.3pt {{C_2} = – x + \frac{1}{x} + {A_2} } \end {align*} $$
توجه داشته باشید که ضرایب $$A_1$$ و $$A_2$$ ثابتهای انتگرالگیری هستند. نهایتا پاسخ عمومی معادله ناهمگن نیز به صورت زیر بدست میآید.
$$ \large \begin {align*} y \left ( x \right ) & = { { C _ 1 } \left( x \right) { x ^2 } + { C _ 2 } \left( x \right)x } \\ & = {\left( {\ln x – \frac { 1} { { 2 { x^ 2 } } } + {A_1}} \right){x^2} } + { \left( { – x + \frac { 1 } { x } + {A_2}} \right)x } \\ & = { {A _1}{ x ^ 2 } + { A _2 } x }+{ {x ^ 2}\left( {\ln x – 1} \right ) }+{ \frac { 1} { 2}} \end {align*} $$
مثال ۲
پاسخ عمومی معادله ناهمگن زیر را بدست آورید. فرض کنید یکی از پاسخهای عمومی معادله ناهمگن برابر با $$ y _ 1 = x $$ باشد.
$$\large { \left( {\ln x – 1} \right) y ^ {\prime\prime} – \frac { { y ^{\prime } }}{ x} + \frac { y } {{ {x ^ 2 } }} }={ \frac{ { { {\left( {\ln x – 1} \right) }^ 2 } }} { x} \;\;}\kern-0.3pt \ \ , {\left( {x \gt e} \right) }$$
بدیهی است که معادله همگن به صورت زیر بیان میشود.
$$ \large { \left( { \ln x – 1} \right ) y ^{ \prime \prime} – \frac { { y ^{\prime} } } { x } }+{ \frac { y} { { {x ^2 } }} } = { 0 } $$
در مطلب معادلات دیفرانسیل مرتبه دوم با ضرایب متغیر، مفهوم فرمول لیوویل را توضیح دادیم. با استفاده از این فرمول رابطه مربوط به رونسکین به صورت زیر ارائه میشود.
$$\large \begin {align*} { { W _{ { y_ 1} , { y _2 } } } \left( x \right) }
& = {\left| {\begin{array}{*{20}{c}}
{{y_1}}&{{y_2}} \\\\ { { y ^{\prime} _1 } } & { { y ^{\prime} _ 2 }}
\end{array}} \right| } \\ & = { {C_1}\exp \left[ { – \int {\frac{{{a_1}\left( x \right)}}{{{a_2}\left( x \right ) }} d x } } \right] \;\;} \\\\ & \Rightarrow
{ { y ^{\prime} _ 2 } { y _ 1 } – { y_ 2 } { y ^ {\prime} _1} } = { { C _ 1 } \exp \left[ { – \int {\left( {\frac{{ – \frac { 1 } { x } } } { { \ln x – 1} } } \right) d x } } \right] } \\ & = {{C_1}\exp \left[ {\int { \frac { { d x }}{ { x\left( {\ln x – 1} \right ) } } } } \right] } \end {align*} $$
به منظور محاسبه انتگرال آخر، از تغییر متغیر زیر استفاده میکنیم.
$$\large { \ln x – 1 = t \;\; } \Rightarrow { \frac { {d x } }{ x } = d t } $$
بنابراین حاصل انتگرال نیز برابر است با:
$$ \large { \int { \frac { { dx } } {{ x \left( {\ln x – 1} \right ) } } } } = { \int { \frac { { d t } }{ t } } } = { \ln t } = { \ln \left ( {\ln x – 1} \right) } $$
در نتیجه معادله رونسکین برابر با عبارت زیر بدست میآید.
$$\large \begin {gather*} { { y ^ { \prime } _ 2 } { y _ 1 } – { y _ 2 }{ y ^ { \prime} _ 1 } } = { { C _ 1 } { e ^ { \ln \left( { \ln x – 1} \right ) } } } \\~\\ \Rightarrow { { y ^ { \prime } _ 2 } { y _ 1 } – { y _ 2 } { y ^ { \prime } _ 1 } } = { { C _ 1 } \left ( { \ln x – 1} \right) } \end {gather*} $$
با تقسیم کردن طرفین عبارت فوق به $$ y _ 1 ^ 2 $$، عبارت زیر بدست خواهد آمد.
$$ \large \begin {gather*} { \frac { { { y ^ { \prime } _ 2 } { y _ 1 } – { y _ 2 } { y ^ { \prime } _ 1 } } } { { y_ 1 ^ 2 } } } = { \frac{{{C_1}\left ( { \ln x – 1} \right ) } } { {y_1^2 } } \;\; } \\~\\ \Rightarrow { { \left( {\frac { { { y _ 2 } } } { { { y _ 1 } } } } \right ) ^ \prime } = \frac { { { C _ 1} \left( {\ln x – 1} \right) } } { { { x ^2 } } } } \Rightarrow {\frac { { { y _ 2} } } { { {y _ 1 }} } = {C_1}\int { \frac { { \ln x – 1} } { { { x ^ 2 } } } d x } } \end {gather*} $$
به منظور محاسبه انتگرال فوق باید از روش جزء به جزء استفاده کرد. در نتیجه توابع $$u,v$$ را به صورت زیر در نظر میگیریم.
$$ \large \begin {align*} { u ^ { \prime } = \frac { 1 } {{ { x ^ 2 } } } \;\;} \kern-0.3pt , \ {v = \ln x – 1 \;\; } & \Rightarrow {u = – \frac { 1 } { x } , }\kern-0.3pt { v ^ { \prime } = \frac { 1 }{ x } } \end {align*} $$
بنابراین حاصل انتگرال برابر خواهد بود با:
$$ \large \begin {align*} {\int { \frac { { \ln x – 1 } }{ { { x ^2 } } } d x} } & = {{ – \frac{{\ln x – 1 }} { x } }-{ \int { \left ( { – \frac { 1 } { x } } \right)\left( {\frac { 1 } { x } } \right ) d x } } } \\\\ & = { – \frac { { \ln x – 1 } } { x } + \int { \frac { { d x } } { { { x ^ 2 } } } } } \\\\ & = { – \frac { { \ln x – 1 } } { x } – \frac { 1 } { x } }+{ { C _ 2 } } \end {align*} $$
بنابراین نسبت توابع $$ y $$ برابر خواهد بود با:
$$ \large { \frac { { { y _ 2 } } } { { { y _ 1 } } } = {C_1}\left[ { – \frac { { \ln x – 1 } } { x } – \frac { 1 } { x } + { C _ 2 } } \right] } = { { C _ 1 } \frac { { \ln x } } { x } + { C _ 2 } } $$
در نتیجه تابع $$y_2$$ برابر خواهد بود با:
$$\large \begin {align*} {y_2} & = { y _ 1 } \left( { { C _ 1 } \frac{{\ln x } }{ x } + {C_2}} \right) \\\\ & = {x\left( {{C_1}\frac { { \ln x } } { x } + {C_2}} \right) } = {{C_1}\ln x + {C_2}x } \end {align*} $$
حال به منظور تعیین پاسخ عمومی معادله ناهمگن، باید پاسخ در نظر گرفته شده در معادله همگن و ناهمگن قرار داده شوند. با انجام این کار، سیستم معادلات زیر بدست میآیند.
$$\large \begin {align*} {\left\{ \begin{array}{l}
{ {C ^{\prime} _ 1 } \ln x + {C ^{\prime} _ 2 } x } = 0\\
{{C ^ { \prime } _ 1 } { \left( {\ln x} \right)^\prime }} + {{C^{\prime}_2}{\left( x \right ) ^ \prime } } = {\Large \frac { { \ln x – 1 } } { x } }
\end {array} \right. \;\;} \Rightarrow
{ \left\{ \begin{array} { l }
{ C^ { \prime } _1 } \ln x + {C^ { \prime } _ 2 } x = 0 \\
{\Large \frac { { { C ^ { \prime }_ 1 } }} { x }} + {C ^ { \prime } _ 2 } = {\Large \frac { { \ln x – 1 } } { x }}
\end{array} \right .} \end {align*} $$
به منظور بدست آوردن $$ {C ^{\prime} _1 } $$، معادله اول را در $$x$$ ضرب کرده و معادله دوم را از آن کم میکنیم. در نتیجه خواهیم داشت:
$$ \large { \left\{ \begin{array} { l } { C ^{\prime} _1 } \ln x + {C^{\prime} _ 2 } x = 0 \\ { C ^{\prime} _ 1 } + { C ^{\prime } _ 2 } x = \ln x – 1 \end{array} \right. \;\;} \Rightarrow { { C ^{\prime} _ 1 }\left( {1 – \ln x} \right) }={ \ln x – 1 \;\;} \\~\\ \large \Rightarrow {{C^{\prime} _ 1 } = – 1 } $$
بنابراین مشتق ضریب دوم نیز برابر است با:
$$ \large { - \ln x + { C ^ { \prime } _ 2 } x = 0 \;\; } \Rightarrow { { C ^ { \prime } _ 2 } = \frac { { \ln x } }{ x } } $$
با انتگرالگیری، ضرایب برابرند با:
$$ \large { { { C _ 1 } = \int { \left ( { – 1} \right) d x } } = { – x + { A _ 1 } } } \\~\\ \large { { { C_ 2 } = \int { \frac { { \ln x } } { x }d x } } = {\int {\ln x\, d \left( {\ln x} \right)} } = { \frac { { { { \ln }^ 2 } x} } { 2 } + { A _ 2 } } } $$
بنابراین با بدست آمدن ضرایب، تابع $$y$$ یا همان پاسخ معادله دیفرانسیل، برابر با عبارت زیر بدست خواهد آمد.
$$ \large \begin {align*} y \left ( x \right ) & = { { C _1 } \left ( x \right ) \ln x + { C _ 2 } \left ( x \right ) x } \\~\\ & = { \left ( { – x + { A _ 1 } } \right ) \ln x } + { \left( { \frac { { { { \ln } ^ 2} x } }{ 2} + { A_2 } } \right ) x } \\~\\ & = { { A _ 1 } \ln x + { A _2 } x } + { \frac { x } { 2 } \ln x \left ( { \ln x – 2 } \right ) } \end {align*} $$
مثال ۳
پاسخ عمومی معادله ناهمگنِ زیر را برای مقادیر مثبت $$ x $$ بیابید.
$$ \large \begin {align*} \left ( { x – 1 } \right) y ^ { \prime \prime } – x y ^ { \prime } + y = { \left ( { x – 1 } \right ) ^ 2 } \end {align*} $$
همچنین یکی از پاسخهای عمومی معادله همگن را برابر با $$ \begin {align*} { y _ 1 } = { e ^ x } \end {align*} $$ در نظر بگیرید. در اولین قدم باید با استفاده از مفهوم رونسکین، پاسخ دوم و مستقل نسبت به پاسخ اول را بیابیم. در نتیجه تابع $$y_2$$ به صورت زیر بدست خواهد آمد.
$$ \large \begin {align*} { W _ { { y _ 1} , { y _ 2 } } }\left( x \right) & = {\left| {\begin{array}{*{ 20 } { c } } { { y _ 1 } } & { { y _ 2 } } \\ { { y ^ { \prime }_ 1} } & { { y ^ { \prime } _ 2 } } \end{array}} \right| } \\ & ={ {C_1}\exp \left[ { – \int {\frac { { { a _ 1 } \left( x \right ) } } { { { a_ 2 } \left ( x \right ) } } dx } } \right] } \\\\ & \Rightarrow { { y ^ { \prime } _ 2 } {y_1} – {y_2 } { ^ { \prime }_1} } ={ {C_1}\exp \left[ { – \int {\left( {\frac { { – x }} { { x – 1} }} \right) d x } } \right] } \\ & = { {C_1}\exp \left[ {\int {\frac { x }{ {x – 1 } }d x } } \right] } \\ & = { { C_ 1 } \exp \left[ {\int {\frac { { x – 1 + 1 } } { { x – 1 } } d x } } \right] } \\ & = { { C _ 1 } \exp \left[ {\int {\left( {1 + \frac { 1 } { {x – 1 } } } \right) d x } } \right] } \\ & = { { C _1 }{ e ^ { x + \ln \left| {x – 1} \right|} } } \\ & = {{C_1} { e ^x } { e ^ { \ln \left| {x – 1} \right| } } } = { {C_1}\left( {x – 1} \right) { e ^ x } } \end {align*} $$
در مرحله بعد، طرفین عبارت بدست آمده در بالا را در $$ \frac {1}{y_1^2} $$ یا همان $$ e^{2x} $$ ضرب میکنیم.
$$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \large \begin {align*} × { e ^ { 2 x } } \Rightarrow { \frac { { { y ^ { \prime }_ 2 }{y_1} – {y_ 2 }{ y ^ { \prime } _1 } } } { { y_1^2 } } } & ={ \frac { { { C_ 1 } \left( { x – 1 } \right ) { e ^ x }} } {{y_1^2}}}\Rightarrow {{\left( {\frac { { { y_ 2 } } } { { { y_ 1 } } } } \right ) ^ \prime } } \\ & = {\frac { { { C _ 1 } \left( { x – 1 } \right ) { e ^ x} } } { {{ e ^{ 2 x } }} } } \\ & = {{C_1}\left( {x – 1} \right) { e ^ { – x } } }
\end {align*} $$
نهایتا با انتگرالگیری از نسبت بدست آمده در بالا خواهیم داشت:
$$ \large \begin {align*} {\frac{{{y_2}}}{{{y_1} } } } & = { {C_1}\int {\left( {x – 1} \right){e^{ – x} } d x } } = {\left[ {\begin{array}{*{20}{l}} { u ^ { \prime } = { e ^ { – x } } } \\ {v = x – 1} \\ {u = – {e^{ – x}}}\\
{ v ^{\prime} = 1} \end {array}} \right] } \\\\ & = { { C_1}\Big[ { – \left( {x – 1} \right){e^{ – x}} }}-{{ \int {\left( { – {e^{ – x } } } \right)dx} } \Big] } \\\\ & = { { C _ 1 } \Big[ { – \left( {x – 1} \right) { e ^ { – x}} }}+{{ \int {{e^{ – x}}dx} } \Big] } \\\\ & = { { C _ 1 } \left[ { – \left( {x – 1} \right ) { e ^ { – x}} – {e^{ – x}}} \right] }+{ {C_2} } \\\\ & = { – { C _ 1 } x { e ^{ – x } } + { C _ 2 } } \end {align*} $$
بنابراین سیستم پاسخها از دو ترم $$e^x$$ و $$x$$ تشکیل شده است. از این رو پاسخ عمومی معادله همگن را میتوان مطابق با رابطه زیر نوشت.
$$ \large { y _ 0 } \left ( x \right ) = { C _ 1} { e ^ x } + { C _2 } x $$
از این رو پاسخ معادله ناهمگن را باید به صورت زیر در نظر گرفت.
$$ \large { y \left( x \right) }={ { C _ 1 } \left ( x \right ) { e ^ x } + { C _ 2 } \left ( x \right ) x } $$
با قرار دادن پاسخ در نظر گرفته شده در دو معادله همگن و ناهمگن، سیستم معادلات زیر بدست خواهد آمد.
$$ \large \left\{ \begin{array}{l} {C^{\prime}_1}{e^x} + { C ^{\prime} _2 } x = 0\\
{{C^{\prime}_1} {e ^x } + { C ^ { \prime}_2} \cdot 1 } = { \Large \frac { { { { \left ( { x – 1} \right)} ^ 2 } }} { { x – 1}} }= {x – 1} \end{array} \right. $$
با کم کردن معادله دوم از معادله اول، ضریب $$C^{\prime}_2$$، مطابق را عبارت زیر بدست خواهد آمد.
$$ \large { { C ^ { \prime } _ 2 } \left ( { x – 1 } \right) = – \left( {x – 1} \right) \;\; }\Rightarrow { { C ^ { \prime } _ 2 } = – 1 } $$
بنابراین ضریب $$C^{\prime}_1$$ نیز برابر با عبارت زیر بدست خواهد آمد.
$$ \large { { C ^ { \prime } _ 1 } { e ^ x } – x = 0 \;\; }\Rightarrow { { C ^ { \prime } _ 1 } = \frac { x } { { { e ^ x} } } = x { e ^ { – x } } } $$
در آخر با انتگرالگیری، خودِ ضرایب برابر با عبارات زیر بدست میآید.
$$ \large { { C _ 2 } = \int { \left ( { – 1 } \right) d x } } = { – x + { A _ 2 }} $$
$$ \large \begin {align*} {{C_1} = \int {x{e^{ – x } } d x } }
= {\left[ {\begin{array}{*{20}{l}} { v = x} \\ { u ^ { \prime } = { e ^ { – x } } } \\ { u = – { e ^ { – x } } } \\ { v ^ { \prime} = 1} \end {array}} \right] } & = {- x { e ^ { – x } } – \int {\left( { – { e ^ { – x} } } \right ) d x } } \\\\ & = {- x { e ^ { – x } } – { e ^ { – x } } + { A _ 1 } } \end {align*} $$
نهایتا با بدست آمدن ضرایب، پاسخ عمومی معادله ناهمگن نیز برابر با خواهد بود با:
$$\large \begin {align*} {y\left( x \right) } & ={ {C_1}\left( x \right){e^x} + {C_2}\left( x \right)x } \\\\ & = {\left( { – x{e^{ – x}} – {e^{ – x}} + {A_1}} \right){e^x} }+{ \left( { – x + {A_2}} \right)x } \\\\ & = { – x – 1 + {A_1}{e^x} }-{ {x^2} + {A_2}x } \\\\ & = {{A_1}{e^x} + {A_2}x } - { { x ^ 2 } – x – 1 } \end {align*} $$











