معادلات دیفرانسیل مرتبه دوم با ضرایب متغیر — از صفر تا صد (+ دانلود فیلم آموزش گام به گام)

در راستای معرفی مفاهیم مربوط به معادلات دیفرانسیل، در این مطلب قصد داریم تا نحوه حل معادلات دیفرانسیل مرتبه دوم با ضرایب متغیر را توضیح دهیم. از این رو به منظور درک بهتر پیشنهاد می‌شود مطالب معادلات دیفرانسیل مرتبه دوم و معادلات دیفرانسیل را مطالعه فرمایید.

مقدمه

توجه داشته باشید که هدف ما یافتن پاسخ معادله دیفرانسیل مرتبه دوم خطی است. از این رو در ابتدا باید با شکل کلی این نوع از معادلات آشنا باشید. شکل کلی یک معادله دیفرانسیل مرتبه دوم با ضرایب متغیر به صورت زیر است.

$$\large { y ^ { \prime \prime } + { a _ 1 } \left ( x \right ) y ^ { \prime } } + { { a _ 2 } \left ( x \right ) y } ={ 0 }$$

فیلم آموزش معادلات دیفرانسیل + حل سوالات کنکور کارشناسی ارشد در فرادرس

کلیک کنید

این نکته را نیز در نظر بگیرید که ضرایب $$a_1(x)$$ و $$a_2(x)$$، توابعی پیوسته بر بازه $$\left [ { a , b } \right ]$$ هستند.

رونسکین

توابع $${ y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right ) , \ldots , { y _ n } \left ( x \right )$$ را در نظر بگیرید. به این توابع در صورتی وابسته خطی گفته می‌شود که ضرایبی همچون $${ \alpha _ 1 } , { \alpha _ 2 } , \ldots , { \alpha _ n }$$ وجود داشته باشند که رابطه زیر را برابر با صفر کنند.

$$\large { { \alpha _ 1 } { y _ 1 } \left ( x \right ) + { \alpha _ 2 } { y _ 2 } \left ( x \right ) + \ldots } + { { \alpha _ n } { y_ n } \left ( x \right ) } \equiv { 0 }$$

اگر رابطه فوق تنها در زمانی درست باشد که تمامی ضرایب $$\alpha$$ برابر با صفر باشند($${ \alpha _1 } = { \alpha _ 2 } = \ldots$$)، در این صورت توابع $$y$$ مستقل خطی‌اند. در مواردی که تنها با دو تابع سروکار داریم، این استقلال را می‌توان به صورتی ساده‌تر بیان کرد. در این حالت، اگر کسر زیر مخالف عددی ثابت باشد، در این صورت دو تابع نسبت به هم مستقل خطی‌اند. توجه داشته باشید که توابع $$y_1(x)$$ و $$y_2(x)$$ دو تابع فرضی هستند که هدف بررسی وابستگی آن‌ها است.

$$\large \frac { { { y _1 } \left ( x \right ) } }{ { { y _ 2 } \left ( x \right ) } } \ne \text {const }$$

در غیر این صورت دو تابع نسبت هم وابسته خطی‌اند. حال به منظور بررسی وابستگی $$n$$ تابع، در ابتدا توابع $${ y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right), \ldots , { y _ n } \left ( x \right )$$ را در نظر بگیرید. فرض کنید برای این توابع مشتق مرتبه $$n-1$$ام وجود دارد. هم‌چنین در نظر بگیرید که این توابع تا $$n-1$$ مشتق‌پذیر باشند. در این صورت به دترمینان زیر، رونسکین این توابع یا به طور کوتاه رونسکین گفته می‌شود.

$$ \large {W\left( x \right) = {W_{{y_1},{y_2}, \ldots ,{ y _ n } } } \left ( x \right ) }<br /> = {\left| {\begin{array}{*{20} { c } } { { y _ 1 } } & { { y _ 2 } } & \ldots &{{y_n}}\\<br /> {{y ^{\prime} _ 1 } } & { { y ^ { \prime } _ 2 } } & \ldots & { { y ^ { \prime } _ n } } \\<br /> \ldots & \ldots & \ldots & \ldots \\ { y _ 1 ^ { \left( {n – 1} \right ) } } & { y _ 2 ^ { \left ( { n – 1 } \right)}}& \ldots &{y_n^{\left( {n – 1 } \right ) } } \end{array}} \right|}$$

آزمون رونسکین

اگر سیستم توابع $${ y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right), \ldots , { y _ n } \left ( x \right )$$ روی بازه $$[a,b]$$ به صورت خطی وابسته باشند، در این صورت رونسکین تابع روی این بازه برابر با صفر است. از طرفی اگر رونسکین غیر صفر باشد، در این صورت توابع $${ y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right), \ldots , { y _ n } \left ( x \right )$$ در حداقل یک نقطه مستقل خطی است. این ویژگی رونسکین به ما می‌گوید که آیا پاسخ‌های یک معادله همگن، مستقل خطی هستند یا خیر.

سیستم‌ پاسخ‌های پایه

دو پاسخ خصوصی مستقلِ یک معادله دیفرانسیل همگن مرتبه دوم، تشکیل‌دهنده سیستم پاسخ‌های پایه معادله مذکور هستند.

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

در حقیقت اگر $${ y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right )$$، سیستم‌ پاسخ‌های پایه‌ای اولیه باشند،‌ در این صورت پاسخ عمومی یک معادله مرتبه دوم را می‌توان به صورت زیر عنوان کرد.

$$\large { y \left ( x \right) } = { { C _ 1 } { y _ 1 } \left ( x \right ) + { C _ 2} { y _2 } \left ( x \right ) }$$

در رابطه فوق $$C$$ها ضرایبی ثابت هستند. جالب است بدانید که اگر دو پاسخ پایه $${ y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right )$$ معلوم باشند، در این صورت می‌توان معادله دیفرانسیل مرتبط با آن‌ها را تعیین کرد. در حالتی که با معادله‌ای از مرتبه دو سر و کار داریم، این معادله دیفرانسیل، برابر با دترمینان ماتریس زیر است.

$$\large \left| {\begin{array}{*{20} { c } } { { y _ 1} } & { { y_2}} & y \\ { { y ^ { \prime } _ 1 } } & { { y ^ {\prime} _ 2 } } & y ^ { \prime } \\ { { y ^ { \prime \prime} _ 1} } & { { y^ { \prime \prime } _ 2 } } & y ^ { \prime \prime } \end{array} } \right| = 0 $$

فرمول لیوویل

بنابراین همان‌طور که در بالا نیز اشاره شد، پاسخ عمومی یک معادله دیفرانسیل همگن، ترکیبی خطی از دو پاسخ خصوصیِ مستقلِ $${ y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right )$$ است. بدیهی است که پاسخ خصوصی وابسته به ضرایب معادله دیفرانسیل خواهد بود. فرمول لیوویل رابطه‌ای را میان رونسکین یا همان $$W(x)$$ که با استفاده از پاسخ‌های پایه‌ایِ $$y_1(x)$$ و $$y_2(x)$$ بدست آمده و ضریب $$a_1(x)$$ بیان می‌کند.

به منظور بدست آوردن این فرمول در ابتدا $$W(x)$$ را برابر با رونسکین تابع در نظر بگیرید. هم‌چنین پاسخ‌های خصوصی معادله دیفرانسیل زیر را برابر با $${ y _ 1 } \left ( x \right ) , { y _ 2 } \left ( x \right )$$ در نظر بگیرید.

$$\large { y ^ { \prime \prime } + { a _ 1 } \left ( x \right ) y ^ { \prime } } + { { a _ 2 } \left ( x \right ) y } = { 0 }$$

توجه داشته باشید که دو ضریب $$a_1(x)$$ و $$a_2(x)$$ روی بازه $$[a,b]$$ پیوسته هستند. فرض کنید نقطه $$x_0$$ در این بازه قرار دارد. در این صورت به ازای $$x \in \left [ { a , b } \right ]$$، فرمول لیوویل به صورت زیر بیان می‌شود:

$$\large { W \left( x \right ) } = { W \left ( { { x _ 0 } } \right ) \exp \left ( { – \int\limits _ { { x _0 } } ^ x { { a _1 } \left ( t \right ) d t } } \right ) }$$

حل معادله دیفرانسیل همگن مرتبه دو

متاسفانه روشی کلی به منظور یافتن پاسخ خصوصی یک معادله وجود ندارد. معمولا پاسخ خصوصی با استفاده از شکل و ضرایب معادله، حدس زده می‌شود. اگر پاسخ خصوصی $${ y _ 1 } \left ( x \right ) \ne 0$$، جوابی برای معادله همگن مرتبه دو باشد، می‌توان آن را با استفاده از تغییر متغیر $$y = { y _ 1 } \left ( x \right ) z \left ( x \right )$$ به معادله‌ای از مرتبه اول تبدیل کرد. هم‌چنین در این موارد از تبدیل $$z ^ { \prime } \left ( x \right ) = u$$ نیز استفاده می‌شود.

روش دیگر کاهش مرتبه معادله دیفرانسیل، مبتنی بر فرمول لیوویل است. در این روش پاسخ خصوصی $$y_1(x)$$ باید معلوم باشد. در ادامه چندین مثال ارائه شده که در آن‌ها روش‌های مختلف حل معادلات دیفرانسیل مرتبه دوم نیز ارائه شده است.

مثال ۱

وضعیت وابستگی دو تابع $${ y _1 } \left ( x \right ) = x + 2$$ و $${ y _ 2 } \left ( x \right ) = 2 x – 1$$ به چه صورت است.

همان‌طور که در بالا نیز بیان شد، سریع‌ترین روش به منظور بررسی وابستگی دو تابع، محاسبه تقسیم آن‌ها است. بنابراین این حاصل تقسیم برابر است با:

$$\large \begin {align*} \frac { { { y _ 1 } \left( x \right)}}{{{y_2}\left( x \right)}} & = {\frac{{x + 2 } } { {2 x – 1}} } \\ & = {\frac { { x – \frac { 1 } { 2 } + \frac{5}{2}}}{{2x – 1}} } = {\frac { { \frac{ 1 } { 2 } \left( {2x – 1} \right ) + \frac { 5 } {2 } } } { { 2 x – 1 } } } \\ & = { \frac { 1 } { 2 } + \frac { 5 } { { 2 \left( {2x – 1} \right ) } } } = {\frac { 1 } { 2 } + \frac{5}{{4x – 2 } } } \end {align*}$$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

همان‌طور که می‌بینید حاصل تقسیم برابر با عددی ثابت نیست؛ بنابراین این دو تابع مستقل خطی‌اند.

مثال ۲

رونسکین دو تابع $${ y _1 } \left ( x \right ) = \cos x$$ و $${ y _ 2 } \left ( x \right ) = \sin x$$ را بیابید.

رونسکین دو تابع برابر با دترمینان زیر است.

$$ { { W _{ { y _ 1 } , { y _ 2 } } } \left( x \right) } = { \left| { \begin {array}{*{20}{c}}<br /> { { y _ 1 } \left( x \right ) } & { { y _ 2 } \left ( x \right ) } \\ { { y ^ { \prime } _ 1 } \left( x \right ) } & { { y ^ { \prime } _ 2 } \left ( x \right ) }<br /> \end {array}} \right| } $$

در نتیجه با قرار دادن دو تابع سینوس و کسینوس در رابطه فوق، اندازه رونسکین برابر است با:

$$ \large { { W_ { { y _ 1 } , { y _ 2 } } } \left ( x \right ) } = { \left| { \begin {array} {*{ 20 } { c } } { \cos x } & { \sin x } \\ { – \sin x } & { \cos x }<br /> \end {array} } \right| } = { { \cos ^ 2 } x + { \sin ^ 2 } x = 1 } $$

با توجه به غیر صفر بودن رونسکین، می‌توان نتیجه گرفت که این دو تابع مستقل خطی‌اند.

مثال ۳

معادله دیفرانسیلی را بدست آورید که پاسخ‌های پایه‌ای آن دو تابع $$x$$ و $$e^x$$ باشد.

فیلم آموزش معادلات دیفرانسیل با میپل Maple در فرادرس

کلیک کنید

در ابتدا باید مشتقات دو تابع را به صورت زیر بدست آوریم.

$$\large { { y ^ { \prime } _ 1 } = x ^ { \prime } = 1 \ \ , \;\;}\kern-0.3pt { {y ^ { \prime \prime } _1 } = 1 ^ { \prime } = 0 }$$

$$\large { { y ^ { \prime } _ 2 } = { \left ( { { e ^ x } } \right ) ^ \prime } = { e ^ x } \ \ ,\;\;}\kern 0.3pt { { y ^ { \prime \prime } _ 2 } = { \left ( { { e ^ x } } \right ) ^ \prime } = { e ^ x } }$$

معادله دیفرانسیل مربوطه باید شرایط زیر را ارضا کند.

$$ \large {\left| {\begin{array}{*{20}{c}} { { y _ 1 } } & { { y _2 } } & y \\ { { y ^ { \prime } _ 1 } } & { { y ^ { \prime } _ 2 } } & y ^ { \prime } \\ { { y ^ { \prime \prime } _ 1} } & { { y ^ { \prime \prime } _ 2 } } & y ^ { \prime \prime } \end {array} } \right| = 0 \; \; } \Rightarrow { \left| { \begin {array}{*{20 } { c } } x & { { e ^ x } }&y\\ 1& { { e ^ x } } & y ^ { \prime } \\ 0 & { { e^ x } } & y ^ { \prime \prime } \end {array} } \right| = 0 }$$

اگر دترمینان را مبتنی بر ستون اول ماتریس بسط دهیم، خواهیم داشت:

$$\large \begin {align*} {{x\left( { { e ^ x }y ^ { \prime \prime } – { e ^ x } y ^ { \prime } } \right) }-{ 1 \cdot \left ( { { e ^ x } y ^ { \prime \prime } – { e ^ x } y } \right ) = 0}} \\ \Rightarrow { { { e ^ x }\left[ {\left( { x y ^ { \prime \prime} – xy ^ {\prime} } \right) }\right.}-{\left.{ \left( { y ^ { \prime \prime } – y } \right ) } \right] = 0 } } \end {align*}$$

با توجه به غیر صفر بودنِ عبارتِ نمایی ($${e^x} \ne 0,$$)، معادله دیفرانسیل برابر با عبارت زیر بدست خواهد آمد.

$$\large { x y ^ { \prime \prime } – x y ^ { \prime } – y ^ { \prime \prime} + y = 0 \;\;} \Rightarrow { \left ( { x – 1} \right ) y ^ { \prime \prime } – x y ^ { \prime } + y = 0 }$$

مثال ۴

پاسخ عمومی معادله $${ x ^ 2 } y ^ { \prime \prime } – 2 x y ^ { \prime } + 2 y = 0$$ را بیابید. فرض کنید یکی از پاسخ‌های خصوصی برابر با $$y_1=x$$ باشد.

همان‌طور که بیان شد در این حالت از تغییر متغیر $$y = { y _ 1 } z = x z$$ استفاده می‌کنیم. بنابراین مشتق $$y$$ برابر است با:

$$\large \begin {align*} y ^ { \prime } & = { \left ( { x z } \right ) ^ \prime } \\ & = z + x z ^ { \prime } ,\kern-0.3pt { y ^ { \prime \prime} = { \left ( { z + x z ^ { \prime } } \right ) ^ \prime } } \\ & = {z ^ { \prime } + z ^ { \prime } + x z ^ { \prime\prime} } \\ & = { 2 z ^{\prime} + x z ^ { \prime \prime } } \end {align*}$$

پس از قرار دادن مشتق محاسبه شده در معادله، به رابطه زیر می‌رسیم.

با جایگذاری $$z ^ { \prime } = p$$ معادله $${ x ^ 3 } p ^ { \prime } = 0$$ بدست خواهد آمد. پاسخ این معادله نیز برابر است با:

$$\large p = { C _ 1 }$$

در نتیجه تابع $$z$$ به صورت زیر بدست می‌آید.

$$\large { p = { C _ 1 } \; \; } \Rightarrow { z ^ { \prime } = { C _ 1 } \; \; } \Rightarrow { z = { C _ 1 } x + { C _2 } }$$

با بدست آمدن $$z$$، تابع $$y$$ به صورت زیر بدست می‌آید.

$$\large { y \left ( x \right ) = x z } = { x \left ( { { C _1 } x + { C _ 2 } } \right ) } = { { C _ 1 } { x ^ 2 } + { C _ 2 } x }$$

مثال ۵

پاسخ عمومی معادله زیر را بیابید.

$$\large \left ( { { x ^ 2 } + 1 } \right ) y ^ { \prime \prime } – 2 y = 0$$

در ابتدا با توجه به شکل تابع، تابعی از درجه ۲ را به عنوان حدس اولیه در نظر می‌گیریم. این تابع به صورت زیر است.

$$\large { y _ 1 } = A { x ^ 2 } + B x + C$$

در نتیجه مشتقات اول و دوم تابع نیز به صورت زیر بدست خواهند آمد.

$$\large { { y ^ { \prime } _1 } = 2 A x + B,\;\;}\kern-0.3pt { { y ^ { \prime \prime } _ 1 } = 2 A }$$

با قرار دادن مشتقات بدست آمده در معادله اصلی، ضرایب ثابت $$A,B,C$$ برابر می‌شوند با:

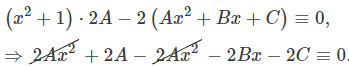
بنابراین رابطه بین ضرایب ثابت به صورت زیر خواهد بود:

$$\large { \left \{ \begin {array} { l } – 2 B = 0 \\ 2 A – 2 C = 0 \end {array} \right. \;\; } \Rightarrow { \left \{ \begin{array} { l } B = 0 \\ A = C \end {array} \right.}$$

در نتیجه شکل تابع به صورت $$y _1 = C \left ( { { x ^ 2 } + 1 } \right )$$ بدست خواهد آمد. بنابراین تابعی به شکل زیر را می‌توان به عنوان یکی از پاسخ‌ها در نظر گرفت.

$$\large { y _ 1 } = { { x ^ 2 } + 1 }$$

با توجه به بدست آمدن $$y_1$$، تغییر متغیر متناظر با آن نیز برابر است با:

$$\begin {align*} y & = {y_1}z = \left( {{x^2} + 1} \right)z \\ & \Rightarrow y ^ { \prime } = 2xz + \left( { { x ^ 2 } + 1 } \right ) z ^ { \prime } \\ & \Rightarrow { { y ^ { \prime \prime } = 2 z + 2 x z ^{\prime} + 2 x z ^ { \prime } } + { \left( { { x ^ 2 } + 1} \right ) z ^ { \prime \prime } } } = { { 2 z + 4 x z ^ {\prime} } + { \left ( { { x ^2 } + 1 } \right )z ^ { \prime \prime } } } \end {align*}$$

در نتیجه با جایگذاری $$y$$ و مشتقاتش در معادله، معادله زیر بدست می‌آید.

$$ \large \begin {align*} \require {cancel} { { \left( {{x^2} + 1} \right) \cdot}\kern0pt{ \left[ {2z + 4 x z ^{\prime} + \left( {{x^2} + 1} \right)z^{\prime\prime}} \right] }-{ 2\left( {{x^2} + 1} \right)z }={ 0}} \\ \Rightarrow {{\left( {{x^2} + 1} \right) \cdot}}\kern0pt{{ \left[ {\cancel { 2 z } + 4xz ^{\prime} + \left( { { x ^ 2 } + 1} \right ) z ^ { \prime \prime } – \cancel { 2 z } } \right] } = { 0 } } \\ \Rightarrow { \left( { { x ^ 2 } + 1} \right)z ^{ \prime \prime } + 4 x z ^ { \prime } = 0 } \end {align*} $$

در این مرحله نیاز است تا از تغییر متغیر دوم نیز استفاده شود. این تغییر متغیر به صورت $$z ^ { \prime } = p \left ( x \right )$$ در نظر گرفته می‌شود. در نتیجه معادله فوق به صورت زیر در خواهد آمد.

$$\large \left ( { { x ^ 2 } + 1 } \right ) p ^ { \prime } + 4 x p = 0$$

حال ما با معادله‌ای از مرتبه اول روبرو هستیم که می‌توان آن را با استفاده از روش جداسازی متغیر‌ها حل کرد. بنابراین حاصل انتگرال برابر است با:

 $$\large \begin {align*} \left( { { x ^ 2 } + 1 } \right ) \frac { { d p} } {{ d x } } = – 4 x p \;\; & \Rightarrow { \frac { { d p } } { p } = – \frac{{4x dx } } {{ { x ^ 2 } + 1}} \;\;} \\ & \Rightarrow { { \int {\frac{{dp}}{p}} }={ – 2\int {\frac { { d \left( {{x^2} + 1} \right)}}{{{x^2} + 1 } } } \;\;}} \\ & \Rightarrow { { \ln \left| p \right| } = { – 2\ln \left( { { x ^ 2 } + 1} \right) }+{ \ln {C_1} \;\; } } \\ & \Rightarrow { \ln \left| p \right| = \ln \frac{ { { C _ 1} } } { { {{\left( { { x ^ 2 } + 1} \right ) }^ 2}}} \;\;} \\ & \Rightarrow {p = \frac { { {C _ 1 } } }{ {{ { \left ( { { x ^ 2 } + 1} \right ) } ^ 2}} } } \end {align*}$$

با بدست آمدن $$p$$، تابع $$z$$ نیز مطابق با رابطه زیر بدست خواهد آمد.

$$\large {p = z ^ { \prime } = \frac { { { C _ 1 } }} { { { { \left ( { { x ^ 2 } + 1 } \right ) } ^ 2 } } } \ } \Rightarrow { z = \int { \frac { { d x } } {{ { { \left ( { { x ^ 2 } + 1} \right ) } ^ 2 } } } } }$$

نحوه محاسبه انتگرال توابع کسری را پیش‌تر توضیح داده بودیم. حاصل این انتگرال به صورت زیر بدست خواهد آمد.

$$\large \begin {align*} \int {\frac { { dx }} { { { {\left( { { x ^ 2 } + 1} \right ) } ^ 2 } } } } &= { \frac { x } { { 2 \left( { { x ^ 2} + 1} \right ) } } } + { \frac { 1 } { 2 } \int { \frac { { d x } } { { { x ^ 2 } + 1 } } } } \\ & = { \frac { x } { { 2 \left ( { { x ^ 2 } + 1 } \right ) } } } + { \frac { 1 } { 2 } \arctan x } + { { C _ 2 } } \end {align*}$$

در نتیجه تابع $$z$$ برابر است با:

$$\large \begin {align*} z & = { C _ 1 } \left[ { \frac { x } { { 2 \left ( { { x ^ 2 } + 1} \right ) } } } \right. + \left. { \frac { 1 } { 2 } \arctan x + { C _ 2 } } \right] \\ & = { \frac { { { C _ 1 } x } } { { { x ^ 2 } + 1} } } + { { C _ 1 } \arctan x } + { { C _ 2 } } \end {align*}$$

بنابراین نهایتا تابع $$y$$ مطابق با رابطه زیر بدست خواهد آمد.

$$\large \begin {align*} y & = \left ( { { x ^ 2 } + 1} \right ) z \\ & = { { C _1 } x } + { { C _ 1 } \left ( { { x ^ 2 } + 1} \right ) \arctan x } + { { C _ 2 } \left ( { { x ^ 2 } + 1} \right) } \\ & = { { C _ 1 } \left [ {x + \left ( { { x ^ 2 } + 1 } \right ) \arctan x } \right] } + { { C _ 2 } \left ( { { x ^ 2 } + 1 } \right ) } \end {align*}$$

مثال ۶

پاسخ عمومی معادله $${ x ^ 2 } y ^ { \prime \prime } – 4 x y ^ { \prime } + 6 y = 0$$ را با استفاده از معادله لیوویل بیابید. فرض کنید یکی از پاسخ‌های خصوصی معادله برابر با $${ y _ 1 } = { x ^ 2 }$$ است.

فیلم آموزش محاسبات انتگرال با متلب و میپل MATLAB و Maple در فرادرس

کلیک کنید

به منظور پاسخ به این سوال در ابتدا $$y_1$$ و $$y_2$$ را برابر با دو پاسخ فرضی در نظر بگیرید. در این صورت فرمول لیوویل به صورت زیر بیان می‌شود.

$$ \large {\begin {align*} W \left( x \right) & = {W_{{y_1},{y_2}}}\left( x \right)<br /> = {\left| {\begin{array}{*{20} { c } } { { y _1 } } & { { y _2 } } \\<br /> { { y ^ { \prime }_1}}& { { y ^ { \prime } _ 2 } } \end {array} } \right| } \\ & = { { W _ 0 } \left ( x \right)\exp \left( { – \int \limits _ {{ x _ 0 } } ^ x { \frac { { { a _1 } \left( t \right ) } } { { {a _ 0 } \left ( t \right ) } } d t } } \right )‌ } \end {align*}} $$

حاصل انتگرال موجود در رابطه فوق نیز به صورت زیر بدست خواهد آمد.

$$\large \begin {align*} \int\limits _ { { x_0 } } ^ x { \frac { { {a _ 1 } \left( t \right)}}{{{a_0}\left( t \right ) }} d t } & = { \int \limits _ { { x _ 0 } } ^ x { \left ( { \frac { { – 4 t } } { { { t ^ 2} } } } \right)dt} } \\ & = {\left. {\left( { – 4 \ln t } \right ) } \right|_ { { x _0 } } ^ x } \\ & = { – 4\ln x + 4 \ln { x _ 0 } } \\ & = { – \ln { x ^ 4 } + \ln x_0^4 } = { – \ln \frac { { { x ^ 4 }} } { { x _0 ^ 4 } } } \end {align*}$$

بنابراین رونسکین نیز به صورت زیر بدست خواهد آمد.

$$ \large \begin {align*} {\left| {\begin{array}{*{20}{c}} { { y _ 1 } } & { { y _2 } } \\<br /> {{y ^ { \prime } _ 1 } } & { { y ^{\prime} _ 2 } } \end{array}} \right| } & = {{W_0}\left( x \right)\exp \left ( {\ln \frac { { { x ^ 4} } } {{ x _0 ^ 4 } } } \right) } \\ & = { \frac { { { W_0}\left( x \right)}}{{x_0^4}}{ x ^ 4 } } = { { C _1 } { x ^ 4 } } \end {align*} $$

با توجه به این‌که $$y_1$$ معلوم است، معادله دیفرانسیلی مرتبه اول برای $$y_2$$ بدست خواهد آمد. با محاسبه رونسکین و برابر قرار دادن آن با عبارت بدست آمده در بالا، داریم:

$$\large \require {cancel} \begin {align*} \left. { { y ^ { \prime } _ 2 } { y_ 1 } – { y _2 } { y ^ { \prime } _ 1 } = { C _ 1 } { x ^ 4 } } \right|:y _ 1 ^ 2 \ \\~\\ \Rightarrow {\frac { { { y ^ { \prime } _2 } { y _ 1 } – { y _2 } { y ^ { \prime } _ 1} } } { { y _ 1 ^ 2} } = \frac { { {C _ 1 } { x ^4 } } } { {y _ 1 ^ 2 } } } \\~\\ \Rightarrow { { \left( {\frac { { { y _ 2 } } } { { { y_ 1 } } } } \right ) ^ \prime } } = {\frac { {{ C _ 1 } { x^ 4 } } } { { y _ 1 ^ 2 } } } = { \frac { { { C _ 1 } \cancel { x ^ 4}} } { { \cancel { x ^ 4 }} } } = { { C _ 1 } } \end {align*} $$

در نتیجه تابع $$y_2$$ برابر خواهد بود با:

$$\large \begin {align*} \frac { { { y_ 2 } } } { { { y _ 1 } } } & = {C_1}x + {C_2} \;\; \Rightarrow { y _ 2 } \\ & = { y _ 1 } \left ( { { C _1 } x + { C _ 2 } } \right ) { { x ^ 2 } \left ( { { C_ 1 } x + { C _ 2 } } \right ) } \\ & = { { C_ 1 } { x ^ 3 } + { C _ 2 }{ x ^2 } } \end {align*}$$

همان‌طور که می‌بینید تابع $$y_2$$، تابع $$y_1$$ را در خود دارد. بنابراین تابع $$y_2$$ را می‌توان برابر با پاسخ عمومی معادله در نظر گرفت.

مثال ۷

پاسخ عمومی معادله $$\begin {align*} { x ^ 2} y ^ { \prime \prime } + x y ^ { \prime } – y = 0 \end {align*}$$ را با استفاده از فرمول لیوویل بیابید. البته پاسخ خصوصی اول را برابر با $${ y _ 1 } = x$$ در نظر بگیرید.

در ابتدا فرمول لیوویل را به صورت زیر می‌نویسیم.

$$ \large { W \left( x \right) = { W _ {{ y _ 1 } , { y _ 2} } } \left( x \right) }<br /> = {\left| {\begin{array}{*{20} { c } } { { y _ 1} } & { {y _ 2 } } \\<br /> {{ y ^{\prime} _ 1 } } &{{y ^ { \prime } _2 } } \end{array}} \right| } = {{C_1}\exp \left( { – \int {\frac{{{a_1}\left( x \right) } } { { { a_ 0 }\left( x \right ) } }d x } } \right) } $$

از طرفی انتگرال موجود در این فرمول نیز برابر خواهد بود با:

$$\large \begin {align*} \int { \frac { { {a _1 } \left ( x \right ) } } {{ { a _ 0 } \left( x \right) } } d x } & = {\int {\frac { x }{ { { x ^ 2 } } } d x } } \\ & = { \int { \frac { { d x } } { x } } } = {\ln \left| x \right| } \end {align*}$$

در نتیجه معادله مد نظر برای بدست آوردن $$y_2$$ برابر است با:

$$\large \begin {align*} { y ^ { \prime } _ 2 } { y _ 1 } – { y _ 2} { y ^ { \prime } _ 1 } = { C _ 1 } { e ^ { – \ln \left| x \right| } } & \Rightarrow { { y ^ { \prime } _2}{y_1} – { y _ 2 } { y ^ { \prime } _1} = { C _1 } { e ^ { \ln \large\frac{1}{ { \left| x \right| } } \normalsize } }} \\ & \Rightarrow { { y ^ { \prime } _ 2 } { y _ 1 } – { y _ 2 } { y ^{\prime} _ 1 } = \frac { { { C_ 1 } } } { x } } \end {align*}$$

با تقسیم کردن طرفین رابطه فوق به $$y _ 1 ^ 2 = { x ^ 2 }$$، نسبت دو پاسخ برابر می‌شود با:

$$\large \begin {align*} {\frac { { { y ^{\prime} _ 2 } { y _ 1 } – {y_2}{y^{\prime}_1}}}{ { y_ 1 ^ 2 } } = \frac{{{C_ 1 } } } { { x y _ 1^ 2 } } } & \Rightarrow { { \left ( { \frac { { {y_2 } }} { { { y _ 1 } } } } \right)^\prime } = \frac{{ { C_ 1 } } } { {x \cdot { x ^ 2 } } } = \frac{{ { C _1 } }} {{{ x ^ 3} } } } \\ & \Rightarrow {\frac { { {y _ 2} } } { { { y _1 } } } = \int {\frac { { { C_ 1 } } } { {{ x ^ 3 }}} d x} } = { – \frac { { { C_ 1 } } } {{ 2 { x ^2 } } } + {C_2} }={ \frac { { {C _1 } } } { {{ x ^ 2 } }} + {C _ 2 } } \end {align*}$$

در این مرحله ثابتِ $$- \frac { C _ 1 } { 2 }$$ را برابر با $$C_1$$ در نظر می‌گیریم ($$– { \large \frac { { { C _ 1 } } } { 2 } \normalsize} \to { C _ 1 }$$). در نتیجه نهایتا پاسخ معادله دیفرانسیل برابر است با:

$$\large \begin {align*} { y _ 2 } = {y_1}\left( {\frac { { {C _ 1 } }} { {{ x ^2 } } } + { C _ 2} } \right) & = { x \left( {\frac { { { C _1 } } } {{ { x ^2 } } } + { C _2 } } \right ) } \\ & = { \frac { { { C _ 1} } } { x } + { C _ 2 } x } \end {align*}$$