معادلات دیفرانسیل مرتبه دوم – به زبان ساده

در حالت کلی دو تعریف به منظور معرفی معادلات دیفرانسیل همگن وجود دارد و ابتدایی‌ترین آن مربوط به معادلات دیفرانسیل همگن مرتبه اول می‌شود. این تعریف معادلاتی را که قالب آن‌ها به صورت زیر است در بر می‌گیرد.

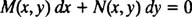
معادله مذکور زمانی همگن است که هر دو تابع M و N، همگن و از یک درجه باشند. تعریف دیگری که به منظور ‌توصیف معادلات دیفرانسیل استفاده می‌شود، بیان می‌کند که تمامی ضرایبِ تابع و مشتقات آن همگن هستند و هم‌چنین سمت دیگر معادله بایستی صفر باشد. برای مثال تابع زیر از مرتبه دوم و همگن است.

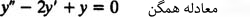
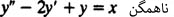
بخش اول: تعیین جواب کلی یک معادله دیفرانسیل مرتبه دوم

در حالت کلی قالب یک معادله مرتبه دوم غیرهمگن به صورت زیر است:

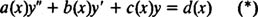
اگر سمت راست همین معادله به جای (d(x صفر قرار گیرد، معادله مفروض تبدیل به یک رابطه همگن خواهد شد و داریم:

$$a(x) y^{\prime \prime}+b(x) y^{\prime}+c(x) y=0\quad (**)$$

دقت شود که حل یک معادله ناهمگن به حل همگن همان معادله مرتبط است. مثلا برای حل معادله * در ابتدا سمت راست آن را صفر قرار می‌دهیم، سپس معادله را حل می‌کنیم، پس از آن با استفاده از روش‌هایی که در ادامه آمده اند، به پاسخ دقیق معادله ناهمگن دست خواهیم یافت.

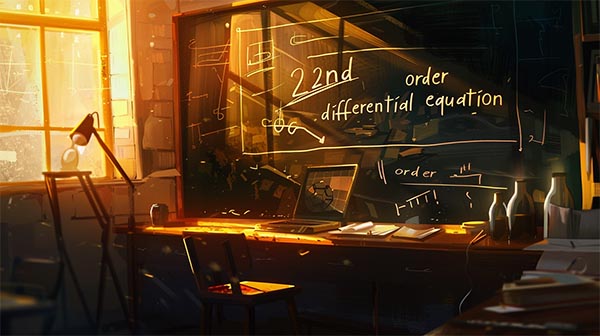
قضیه اول

اگر (y₁(x و (y₂(x، جواب‌های مستقل خطی از یک معادله همگن باشند، هر ترکیب خطی از این دو تابع نیز جوابی برای معادله دیفرانسیل مذکور خواهد بود. بنابراین با فرض (y₁(x و (y₂(x هر کدام به تنهایی در معادله صدق کنند، می‌توان گفت تابع زیر نیز در معادله اصلی صادق خواهد بود.

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

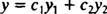
قضیه دوم

اگر $$\bar{y}$$ پاسخ خاص معادله غیر‌همگن * باشد و (y_h(x نیز پاسخ عمومی معادله ** محسوب شود، در نتیجه جواب زیر پاسخی از معادله ** خواهد بود.

$$y=y_h+$$\bar{y}$$$$

بنابراین در حالت کلی می‌توان گفت که:

جواب خاص معادله ناهمگن + جواب عمومی معادله همگن مرتبط با آن = جواب کلی معادله ناهمگن خطی

در ادامه راجع به نحوه پیدا کردن این دو پاسخ بحث خواهد شد. قضیه اول به منظور استفاده در تمامی معادلات همگن با هر مرتبه‌ای کاربرد دارد. به جرات می‌‎توان گفت که قضایای اول و دوم، مهم‌ترین مفاهیم ارائه شده در معادلات دیفرانسیل هستند، بنابراین به خاطر سپردن آن‌ها می‌تواند بسیار مفید باشد.

مثال 1

معادله زیر را در نظر بگیرید.

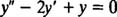
اگر دقت کنید پاسخ‌های زیر در این معادله صادق خواهند بود. [در ادامه در مورد نحوه پیدا کردن این پاسخ‌ها بحث خواهیم کرد.

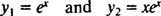
بنابراین هر ترکیب خطی از این معادلات نیز پاسخی برای معادله مذکور خواهد بود. در نتیجه پاسخ عمومی این معادله برابر است با:

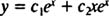
دقت شود که برای هر ثابت c₂ و c₁ تابع y در معادله مد نظر، صدق می‌کند. با در نظر گرفتن پاسخ عمومی و محاسبه مشتق اول و دوم آن و هم‌چنین جایگذاری این مشتقات در معادله، ثابت می‌شود که این پاسخ عمومی در معادله صدق خواهد کرد.

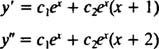
بنابراین با جایگذاری این روابط در معادله اصلی خواهیم داشت:

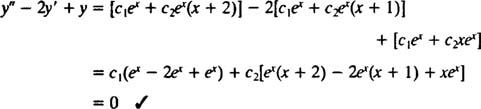
در نتیجه هر ترکیب خطی از این دو پاسخ، جوابی برای معادله مفروض خواهد بود.

مثال 2

نشان دهید که رابطه y=4x-5 در معادله زیر صدق می‌کند.

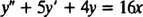
سپس با فرض این‌که روابط y₁=e-x و y₂=e-4x این معادله را ارضا می‌کند، پاسخ کلی این معادله ناهمگن را بدست آورید. در ابتدا به منظور ثابت کردن این‌که، معادله y=4x-5، پاسخی از معادله غیرهمگن است، تابع y در معادله اصلی جایگذاری خواهد شد. بدین منظور عبارات 4=′y و 0=″y قابل محاسبه هستند. بنابراین با جایگذاری این عبارات در معادله مورد بحث، عبارت زیر حاصل خواهد شد:

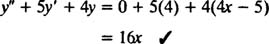
حال با توجه به این‌که دو تابع y₁=e^-x و y₂=e^-4x، از یکدیگر مستقل خطی هستند و بر مبنای قضیه اول، هر ترکیب خطی از این دو رابطه نیز، پاسخی برای معادله مذکور خواهد بود. بنابراین پاسخ عمومی این معادله برابر است با:

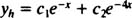
در ادامه قضیه دوم می‌گوید:

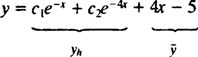
رابطه بالا پاسخ کلی معادله ناهمگن مذکور خواهد بود.

مثال 3

نشان دهید که دو تابع y₁=sinx و y₂=cosx، در معادله همگن 0=y″+y صدق می‌کنند. پس از آن جواب کلی معادله y″+y=x (معادله ناهمگن مرتبط با معادله 0=y″+y) را بیابید.

قدم اول: اگر (y₁=sin(x باشد، عبارت 0=y₁″+y₁ برقرار است. با همین روش می‌توان نشان داد که تابع (y₂=cos(x نیز در معادله اصلی صدق می‌کند. هم‌چنین با توجه به این که این دو تابع از یکدیگر مستقل خطی هستند و هر دو در معادله اصلی صدق می‌کنند، در نتیجه ترکیب خطی آن‌ها که در زیر آمده، پاسخ عمومی معادله مذکور خواهد بود.

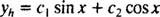
حال به منظور حل معادله ناهمگن y″ + y = x می‌توان با استفاده از روشی که در ادامه در مورد آن بحث خواهیم کرد، پاسخی را برای معادله مفروض حدس زد. به عنوان مثال y=x در این معادله صدق می‌کند. این رابطه به عنوان پاسخ خصوصی معادله مذکور در نظر گرفته شده است. بنابراین پاسخ کلی معادله ناهمگن y″ + y = x برابر است با ترکیب پاسخ عمومی و خصوصی:

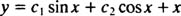
در این بخش در مورد پاسخ یک معادله دیفرانسیل بحث شد. متوجه شدیم که پاسخ یک معادله دیفرانسیل مرتبه دوم ناهمگن برابر است با حاصل جمع پاسخ عمومی و پاسخ خصوصی آن معادله. در دو بخش آینده در مورد تعیین پاسخ عمومی و خصوصی انواع خاصی از معادلات بحث خواهیم کرد.

بخش دوم: تعیین جواب عمومی یک معادله دیفرانسیل با ضرایب ثابت

در این بخش قصد داریم تا در مورد یافتن پاسخ عمومی یک معادله دیفرانسیل با ضرایب ثابت بحث کنیم. معادله‌ای را به صورت زیر در نظر بگیرید:

فیلم آموزش ریاضیات مهندسی پیشرفته + نکات مهم در فرادرس

کلیک کنید

در معادله بالا فرض شده که ضرایب a و b و c ثابت هستند. این رابطه یک معادله دیفرانسیل عمومی با ضرایب ثابت محسوب می‌شود. روشی که در این بخش ارائه خواهد شد فقط برای چنین معادلاتی کاربرد خواهد داشت. به منظور حل چنین معادلاتی ابتدا پاسخ را به صورت y = e^mx در نظر می‌گیریم. سپس با جایگذاری کردن تابع y، در معادله اصلی به یک معادله بر حسب m خواهیم رسید. با بدست آوردن مقادیر m، و جایگذاری آن در تابع y، پاسخ عمومی یافت می‌شود. به منظور درک بهتر به مثال‌های زیر توجه کنید.

مثال 1

پاسخ عمومی معادله دیفرانسیل y″ – y′ – 2 y = 0 را بیابید. در ابتدا پاسخ عمومی به صورت y = e^mx فرض می‌شود. در نتیجه این تابع بایستی در معادله دیفرانسیل اصلی صدق کند. بنابراین در قدم دوم، تابع y در معادله مفروض جایگزین خواهد شد. با جایگذاری داریم:

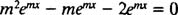
با حذف عبارت e^mx از طرفین (زیرا این عبارت هیچ‌گاه صفر نخواهد شد)، به معادله‌ای بر حسب m، که آن را معادله مشخصه می‌نامیم، دست خواهیم یافت.

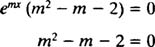
با تجزیه این فرمول به شکل زیر می‌توان به مقادیر m، دست یافت:

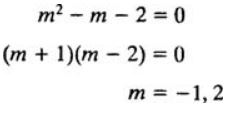
همان‌طور که می‌بینید، دو مقدار برای m پیدا شده است. حال با جایگذاری این مقادیر در تابع y = e^mx به دو معادله y = e^-x و y = e^2x می‌رسیم. دقت کنید که هر دوی این توابع، پاسخ عمومی هستند. بنابراین ترکیب خطی از این دو تابع، پاسخ عمومی معادله در نظر گرفته‌ می‌شود:

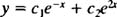
بنابراین توجه کنید که پاسخ عمومی معادله دیفرانسیل همگنی که به صورت زیر است فقط به معادله مشخصه مرتبط وابسته است.

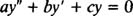
هم‌چنین بایستی توجه نمود، زمانی که چندیدن مقدار m پیدا شده باشند، پاسخ عمومی معادله برابر است با ترکیب خطی توابع یافت شده. بنابراین اگر m₁ و m₂ و ... و m_n، ریشه‌های معادله مشخصه باشند، پاسخ عمومی معادله دیفرانسیل مرتبط با آن برابر است با:

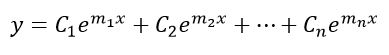
در حالتی که ریشه‌ای تکراری وجود داشته باشد. به عنوان مثال m₂ و m=m₁ ریشه‌های معادله مشخصه باشند، قالب کلی پاسخ عمومی به صورت زیر خواهد بود:

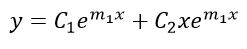
به منظور درک بهتر به مثال بعدی توجه فرمایید.

مثال 2

پاسخ عمومی معادله زیر را بیابید:

 y″ – 2 y′ + y = 0

با فرض y = e^mx و جایگذاری آن در معادله اصلی، معادله مشخصه به صورت زیر خواهد شد:

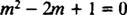
همان‌طور که می‌بینید ریشه‌های این معادله هر دو برابر با 1 هستند. بنابراین پاسخ عمومی این معادله به صورت زیر خواهد بود:

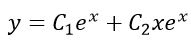
فرض کنید ریشه‌های معادله مشخصه‌ای به صورت m=2,2,-1 باشند؛ در این حالت پاسخ معادله عمومی به صورت زیر در نظر گرفته می‌شود:

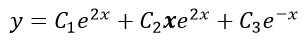
بنابراین، همان‌طور که بیان شد، مهم‌ترین مسئله در حل یک معادله دیفرانسیل همگن با ضرایب ثابت، ریشه‌های معادله مشخصه‌ای است که با فرض y = e^mx حاصل شده.

بخش تعیین جواب خصوصی

همان‌طور که در بخش اول نیز بیان شد، به منظور دستیابی به جواب کامل معادله غیرهمگن خطی به قالب زیر نیازمند هستیم تا پاسخ خصوصی و عمومی مناسب را پیدا کنیم.

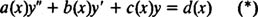
 قضیه دوم بیان می‌کند که پاسخ خصوصی بایستی به ترکیب پاسخ‌های عمومی معادله اضافه شود و عبارت حاصل شده، به عنوان جواب کلی معادله در نظر گرفته می‎شود. در این بخش قصد داریم تا در مورد روش «ضرایب نامعین» (Undetermined Coefficients) در بدست آوردن پاسخ خصوصی معادله دیفرانسیل نامعین بحث کنیم.

دقت شود که این روش در مواردی کاربرد خواهد داشت که در آن‌ها مشتقات تابع (d(x در معادله * با استفاده از تعداد محدودی تابع، قابل نمایش باشند. به عنوان مثال تابع y=sin x را در نظر بگیرید. مشتقات اول تا چهارم این تابع به صورت زیر هستند:

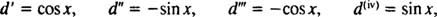
همان‌طور که می‌بینید در این تابع مشتقات به صورت دوره‌ای تکرار می‌شوند یعنی مشتق چهارم با خود تابع برابر است، مشتق اول با پنجم و به همین صورت تکرار می‌شوند. دقت کنید که در چنین توابعی تمامی مشتقات تابع را می‌توان به با تعداد معدودی عبارت نشان داد. مثلا در مورد تابع sin x مشتق nام آن را می‌توان به صورت زیر نشان داد:

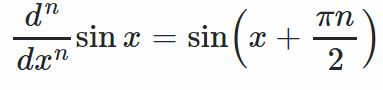
در مقابل بدیهی است که اکثر توابع این ویژگی را نخواهند داشت و مشتقات آن‌ها معدود نخواهند بود. به عنوان نمونه، تابع d(x)=tan x را در نظر بگیرید. مشتقات اول تا چهام آن به صورت زیر هستند:

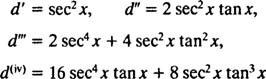
دقت کنید که مشتق nام این تابع شامل عبارت tan^n‐1 x است. بنابراین این تابع هیچ‌گاه مشتقات خود را تکرار نخواهد کرد. از همین رو روش ضرایب نامعین در حل معادله‌ای که عبارت غیر همگن آن tan x باشد، قابل استفاده نخواهد بود.

بر همین اساس روش ضرایب نامعین به منظور تعیین جواب خصوصی در مواردی کاربرد خواهد داشت که در آن‌ها، مشتقات با استفاده از تعداد مشخصی عبارت قابل بیان باشند. در جدول زیر چند تابع که از این ویژگی برخوردار هستند، نشان داده شده است.

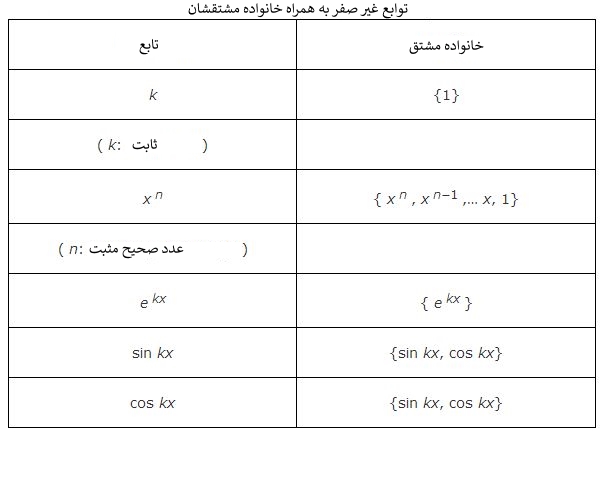
به عنوان مثال تابع d(x) = 5x² را در نظر بگیرید. خانواده مشتقات برای چنین تابعی برابر هستند با: (x², x, 1). به منظور تعیین خانواده مشتق تابعی که از حاصل‌ضرب چند تابع ساخته شده است، خانواده آن‌ها نیز از ضرب این اجزا تشکیل خواهند شد. به عنوان مثال تابع d(x)=xsin 2x را در نظر بگیرید. خانواده مشتقات چنین تابعی برابر هستند:

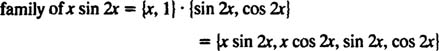
ترکیب خطی چند تابع

ترکیب خطی دو تابع  y₁ و  y₂ برابر است با:

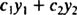
به همین صورت ترکیب توابع y₁ تا y_n برابر هستند با:

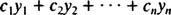
توجه فرمایید که در تمامی این موارد ضرایب c₁  تا c_n، ثابت هستند. به منظور دستیابی به حل خصوصی یک معادله دیفرانسیل ناهمگن، مراحل زیر را انجام دهید:

1. حدس زدن پاسخ خصوصی به صورت ترکیب عبارات خانواده مشتق
2. قرار دادن این حدس در معادله دیفرانسیل اصلی
3. پیدا کردن ثوابت

مثال 1

پاسخ خصوصی معادله زیر را بیابید:

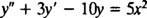
همان‌طور که قبلا نیز بیان شد، خانواده مشتقات تابع d = 5x² برابر هستند با: x² و x و 1. دقت کنید که به منظور تعیین خانواده مشتقات، ضرایب ثابت در نظر گرفته‌ نمی‌شوند. در مرحله دوم پاسخ خصوصی را به صورت ترکیب خطی این عبارات در نظر می‌گیریم. بنابراین خواهیم داشت:

y = Ax² + Bx + C

A و B و C ضرایبی هستند که با جایگذاری پاسخ خصوصی فرض شده در معادله، پیدا خواهند شد. در مرحله سوم با جایگذاری تابع فرض شده در معادله اصلی داریم:

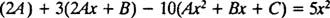
با مرتب کردن این رابطه، عبارت زیر حاصل خواهد شد:

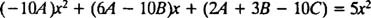
در ادامه با برابر قرار دادن ضرایب x و x² و x⁰ در دو طرف معادله، سه رابطه به منظور پیدا کردن سه ثابت مجهول حاصل خواهد شد:

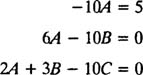
با حل این سه معادله مقادیر زیر بدست می‌آیند:

A=-1/2 و B=-3/10 و C=-19/100

سپس با جایگذاری این سه ثابت در معادله فرض شده، پاسخ خصوصی بدست خواهد آمد که مطابق با فرمول زیر است:

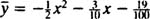
مثال 2

پاسخ خصوصی معادله زیر را بیابید.

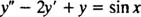
همان‌طور که قبلا نیز بیان شد، خانواده مشتقات تابع sin x، به صورت sin x و cos x، تکرار خواهند شد. بنابراین پاسخ خصوصی این معادله را به صورت زیر در نظر می‌گیریم:

y = A sin x + B cos x

با جایگذاری این تابع در معادله مد نظر، عبارت زیر حاصل خواهد شد:

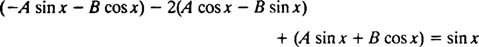
با مرتب کردن عبارت داریم:

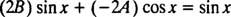
نهایتا با برابر قرار دادن ضرایب sin x و cos x، دو معادله زیر به منظور محاسبه A و B، حاصل خواهد شد:

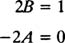
بنابراین با محاسبه A=0 و B=1/2، پاسخ خصوصی معادله دیفرانسیل مذکور به صورت زیر خواهد شد.

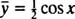
مثال 3

پاسخ خصوصی معادله زیر را بیابید:

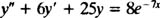
همان‌طور که مشاهده می‌شود با مشتق‌گیری از تابع  e^−7x خود این تابع همواره تکرار خواهد شد. بنابراین خانواده مشتق این تابع برابر با e^−7x در نظر گرفته ‌می‌شود. در نتیجه به منظور دستیابی به پاسخ خصوصی، آن را به صورت معادله  Ae^−7x در نظر می‌گیریم. در مرحله بعد با جایگذاری پاسخ فرض شده در معادله اصلی به عبارت زیر خواهیم رسید:

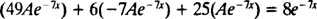
سپس با برابر قرار دادن ضرایب e^−7x در دو طرف این معادله خواهیم دید که:

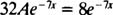
بنابراین 32A=8 خواهد شد که به این معنی است: A=1/4. در نتیجه با محاسبه این ضریب ثابت، می‌توان پاسخ خصوصی را به صورت زیر بیان کرد:

y=¼ e^−7x