مساحت مربع داخل دایره چگونه بدست می آید؟ — به زبان ساده + تمرین و مثال

مساحت مربع داخل دایره برابر «حاصلضرب قطر دایره محیطی تقسیم بر دو» است. به عبارت دیگر، اگر قطر دایره محیط بر مربع را داشته باشیم و آن را در خودش ضرب کنیم، مساحت مربع محاطی برابر عدد به دست آمده تقسیم بر دو خواهد شد. علاوه بر این روش، امکان محاسبه مساحت مربع محاطی با اندازه محیط دایره نیز وجود دارد. در این آموزش، به معرفی فرمولها و نحوه محاسبه مساحت مربع داخل دایره به همراه حل چندین مثال متنوع و کاربردی میپردازیم.
چندضلعی محاطی چیست؟
اگر بتوانیم دایرهای را رسم کنیم که از روی تمام راسهای یک چندضلعی عبور کند، به آن چندضلعی، محاطی میگوییم.
تصویر زیر، نمونهای از یک سهضلعی، چهارضلعی (مربع) و پنجضلعی محاطی را نمایش میدهد.
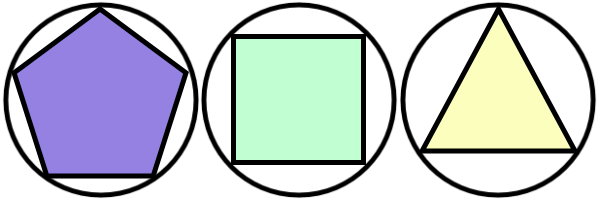
مساحت مربع داخل دایره چگونه محاسبه میشود؟
مساحت مربع داخل دایره، بر اساس خواص چندضلعیهای محاطی و رابطه مساحت مربع محاسبه میشود. فرمول مساحت مربع عبارت است از:
خودش × اندازه یک ضلع = مساحت مربع
در صورتی که اندازه قطر مربع مشخص باشد، امکان محاسبه مساحت با استفاده از رابطه زیر نیز وجود خواهد داشت:
۲ ÷ (قطر × قطر) = مساحت مربع
برای درک بهتر نحوه محاسبه مساحت مربع داخل دایره، شکل زیر را در نظر بگیرید. محاسبه مساحت مربع معمولا با استفاده از اندازه ضلع یا قطر آن انجام میشود.
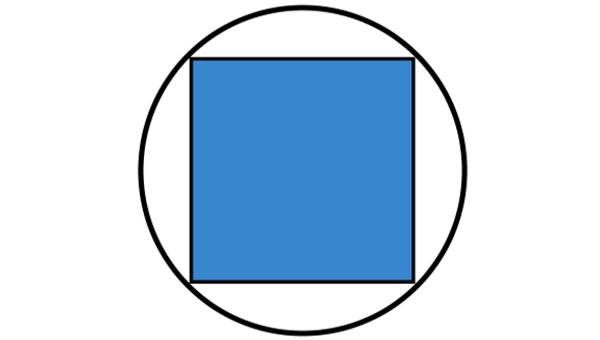
ضلعهای مربع بالا، وتر دایره محیطی هستند. بنابراین، اگر اندازه وتر دایره را داشته باشیم، میتوانیم مساحت مربع محاطی را حساب کنیم. یکی از خواص مهم مربع محاط در دایره این است که قطرهای آن، همواره از مرکز دایره محیطی عبور میکنند.
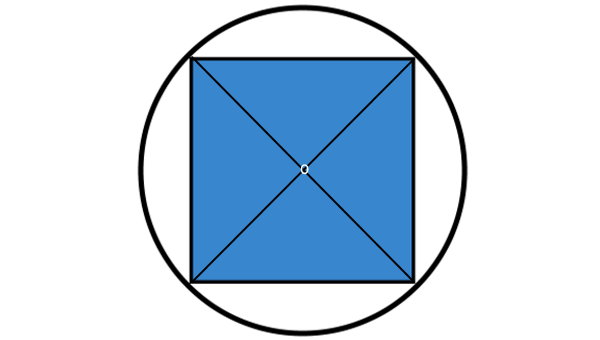
با توجه به تصویر بالا، قطرهای مربع محاطی، وترهای دایره محیطی هستند. این قطرها از مرکز دایره عبور میکنند. بنابراین، قطر مربع محاطی با قطر دایره محیطی برابر است. در نتیجه، با داشتن شعاع یا قطر دایره نیز میتوان مساحت مربع محاط در آن را تعیین کرد.
فرمول مساحت مربع داخل دایره
عبارت جبری مساحت مربع محاطی بر اساس قطر دایره به صورت زیر نوشته میشود:
$$
A = \frac { d^۲ }{۲}
$$
- A: مساحت مربع محاط در دایره
- d: قطر دایره محیطی
زاویه مرکزی مقابل به ضلع مربع محاطی، برابر 90 درجه است. با توجه به این نکته و فرمولهای اندازههای مختلف دایره، نسبت طول کمان به وتر (ضلع مربع)، همواره برابر با ۱/۱۱۰۷ خواهد بود:
۱/۱۱۰۷ = وتر ÷ طول کمان
به این ترتیب، داریم:
۱/۱۱۰۷ ÷ طول کمان = ضلع مربع محاطی
با توجه به نسبت بالا، در صورت مشخص بودن اندازه کمان مقابل به وتر، امکان محاسبه مساحت مربع توسط فرمول اصلی آن فراهم میشود. برای یادگیری بیشتر در رابطه با روشهای محاسبه مساحت مربع با قطر، مطالعه مطلب «مساحت مربع با قطر چگونه بدست میآید؟ – به زبان ساده + حل تمرین و مثال» را به شما پیشنهاد میکنیم.
مثال 1: محاسبه مساحت مربع با شعاع دایره
اگر شعاع دایره نمایش داده شده در تصویر زیر برابر ۴ سانتیمتر باشد، مساحت مربع داخل آن چقدر است؟
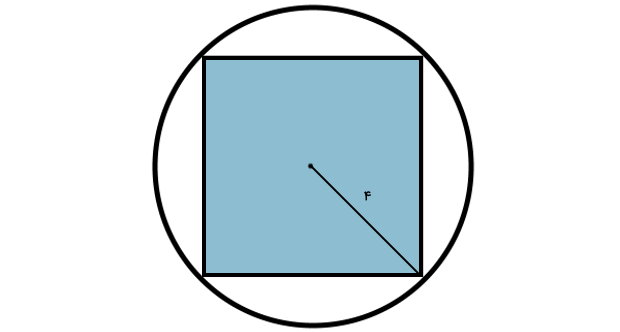
میدانیم که قطر دایره، دو برابر شعاع آن است. به علاوه، قطرهای دایره محیطی و مربع محاطی هماندازه هستند. بنابراین:
۸ = ۴ × ۲ = قطر مربع = قطر دایره
فرمول مساحت مربع با قطر برابر است با:
۲ ÷ (قطر × قطر) = مساحت مربع
اندازه قطر را درون این فرمول قرار میدهیم و آن را حل میکنیم:
۲ ÷ (۸ × ۸) = مساحت مربع
۲ ÷ (۶۴) = مساحت مربع
۳۲ = مساحت مربع
در نتیجه، مساحت مربع محاطی برابر ۳۲ سانتیمتر مربع است.
مثال 2: محاسبه مساحت مربع محاط در دایره از روی طول کمان
تصویر زیر، یک مربع محاط در دایره را نمایش میدهد. طول کمان مقابل ضلع مربع برابر ۱۵ متر است. مساحت مربع محاطی را به دست بیاورید. مقادیر را تا دو رقم اعشار بنویسید.
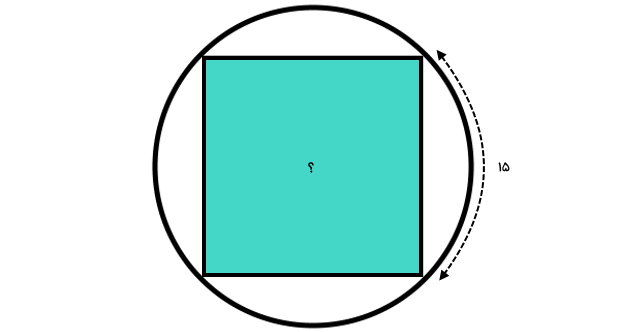
اندازه ضلع مربع محاطی از رابطه زیر به دست میآید:
۱/۱۱ ÷ طول کمان = ضلع مربع محاطی
طول کمان را درون رابطه بالا قرار میدهیم:
۱/۱۱ ÷ ۱۵ = ضلع مربع محاطی
۱۳/۵۰ = ضلع مربع محاطی
مساحت مربع برابر است با:
خودش × یک ضلع = مساحت مربع
۱۳/۵ × ۱۳/۵ = مساحت مربع
۱۸۲/۲۵ = مساحت مربع
در نتیجه، مساحت مربع برابر با ۱۸۲/۲۵ متر مربع است.
مساحت مربع محیطی چگونه محاسبه میشود؟
مربع محیطی، مربعی است که تمام ضلعهای آن بر یک دایره مماس هستند.
تصویر زیر، نمونهای از یک مربع محیط بر دایره را نمایش میدهد.

اگر قطرهای دایره محاطی را از نقطه تماس ضلعهای مماس رسم کنیم، شکل زیر به وجود میآید.
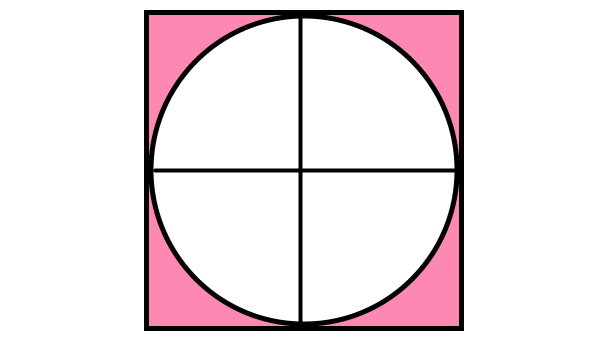
قطرهای رسم شده، با ضلعهای مربع محیطی موازی هستند؛ چراکه زاویه تمام راسهای مربع برابر 90 درجه است و قطر دایره نیز در نقطه تماس بر خط مماس عمود میشود. به همین دلیل، اندازه قطر دایره محاطی با اندازه ضلع مربعِ محیط بر آن برابر است. به این ترتیب، میتوانیم بگوییم:
خودش × قطر دایره محاطی = مساحت مربع محیطی
مثال ۳: محاسبه مساحت مربع محیطی
محیط دایرهای برابر با 84 سانتیمتر است. مساحت مربع محیط بر این دایره را به دست بیاورید. (عدد پی را برابر 3 در نظر بگیرید.)
به منظور تعیین مساحت مربع محیطی، به اندازه قطر دایره محیط در آن نیاز داریم. محیط این دایره داده شده است. بنابراین، با استفاده از فرمول محیط دایره میتوانیم قطر را به دست بیاوریم:
قطر × عدد پی = محیط دایره
قطر × ۳ = ۸۴
۳ ÷ ۸۴ = قطر
۲۸ = قطر
قطر دایره محاطی برابر با ۲۸ سانتیمتر است. از اینرو، اندازه ضلع مربع محیطی نیز برابر با ۲۸ سانتیمتر خواهد بود. مساحت مربع از رابطه زیر به دست میآید:
خودش × یک ضلع = مساحت مربع
۲۸ × ۲۸ = مساحت مربع
۷۸۴ = مساحت مربع
مثال ۴: محاسبه نسبت مساحت مربع محاطی و محیطی
دایرهای با قطر ۱۸ متر را در نظر بگیرید. این دایره بر یک مربع محیط و بر مربع دیگر محاط شده است. نسبت مساحت مربع محیطی به مربع محاطی را حساب کنید.
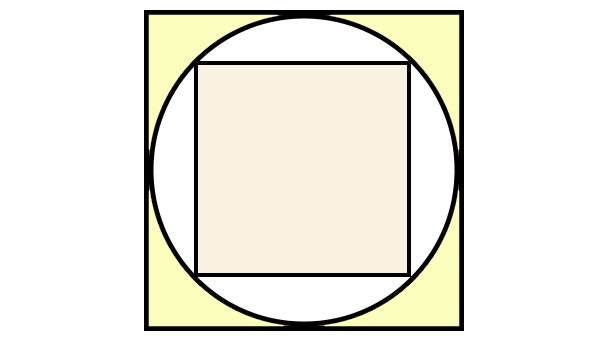
برای درک بهتر مسئله و نحوه حل آن، دو قطر دایره را مطابق با شکل زیر رسم میکنیم.
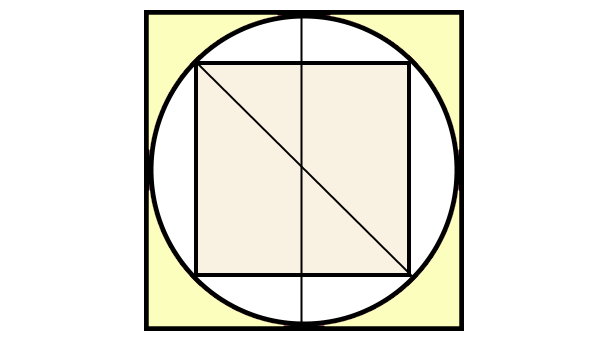
همانطور که مشاهده میکنید؛ یکی از قطرهای دایره برابر با قطر مربع محاطی و قطر دیگر آن برابر با ضلع مربع محیطی است. مساحت مربع محاطی توسط رابطه زیر محاسبه میشود:
۲ ÷ (قطر × قطر) = مساحت مربع محاطی
۲ ÷ (۱۸ × ۱۸) = مساحت مربع محاطی
۲ ÷ (۳۲۴) = مساحت مربع محاطی
۱۶۲ = مساحت مربع محاطی
مساحت مربع محیطی نیز از رابطه زیر به دست میآید:
قطر × قطر = مساحت مربع محیطی
۱۸ × ۱۸ = مساحت مربع محیطی
۳۲۴ = مساحت مربع محیطی
با توجه به نتایج به دست آمده، نسبت مساحت مربع داخل دایره به مساحت مربع بیرون دایره برابر است با:
۲ = ۱۶۲ ÷ ۳۲۴ = نسبت مساحت مربع محیطی به مربع محاطی
در نتیجه، مساحت مربع محیطی، دو برابر مساحت مربع محاطی است. این قضیه برای تمام مربعهای محیطی و محاطی متناظر یک دایره صدق میکند.
حل مثال های مساحت مربع داخل دایره
در این بخش، به حل چند مثال بیشتر در رابطه با محاسبه مساحت مربع محاطی در حالتهای مختلف میپردازیم.
مثال ۵: محاسبه نسبت افزایش مساحت مربع محاطی
اگر قطر یک دایره محیطی، دو برابر شود، مساحت مربع محاط در آن چه تغییری میکند؟
به منظور حل این مسئله، ابتدا فرمول مساحت مربع محاطی را مینویسیم:
$$
A = \frac {d^۲} {۲}
$$
- A: مساحت مربع محاطی
- d: قطر دایره محیطی
اگر قطر دایره محیطی دو برابر شود، d به d۲ تغییر میکند:
$$
A = \frac {(۲d)^۲} {۲}
$$
$$
A = \frac {۴ \times d^۲} {۲}
$$
$$
A = ۴ \times \frac {d^۲} {۲}
$$
همانطور که مشاهده میکنید، با دو برابر شدن قطر دایره محیطی، مساحت مربع محاطی چهار برابر میشود.
مثال ۶: محاسبه مساحت قسمت رنگی
مساحت قسمت رنگی شکل زیر را به دست بیاورید (عدد پی را برابر ۳ در نظر بگیرید).
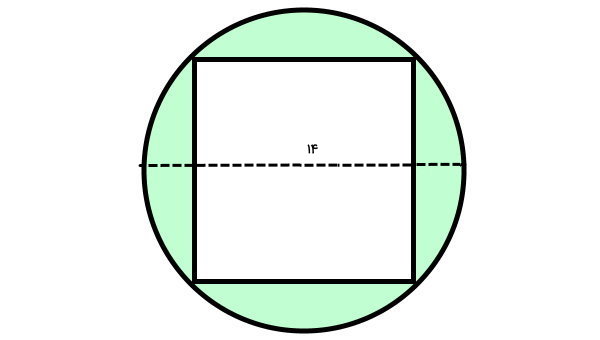
مساحت قسمت رنگی در شکل بالا برابر است با:
مساحت مربع محاطی – مساحت دایره محیطی = مساحت قسمت رنگی
مساحت دایره محیطی از فرمول زیر به دست میآید:
شعاع × شعاع × عدد پی = مساحت دایره
قطر دایره برابر ۱۴ است. بنابراین، شعاع آن برابر ۷ خواهد بود:
۷ × ۷ × ۳ = مساحت دایره
۱۴۷ = مساحت دایره
با توجه به محاطی بودن مربع، مساحت آن به صورت زیر محاسبه میشود:
۲ ÷ (قطر × قطر) = مساحت مربع
۲ ÷ (۱۴ × ۱۴) = مساحت مربع
۲ ÷ ۱۹۶ = مساحت مربع
۹۸ = مساحت مربع
اختلاف دو مساحت به دست آمده، مساحت ناحیه رنگی است:
۹۸ – ۱۴۷ = مساحت قسمت رنگی
۴۹ = مساحت قسمت رنگی
مثال ۷: محاسبه مساحت مربع داخل دایره از روی محیط دایره
محیط دایرهای برابر برابر ۱۰۰ سانتیمتر است. مساحت مربع محاطی در آن را محاسبه کنید.
راسهای مربع محاطی، محیط دایره را به چهار کمان برابر تقسیم میکنند. به عبارت دیگر، طول کمان مقابل به ضلع مربع محاطی، یکچهارم محیط دایره است. اگر محیط یک دایره را داشته باشیم، طول هر کمان مقابل به ضلع مربع محاطی برابر یکچهار محیط دایره خواهد بود. به این ترتیب، داریم:
۲۵ = ۴ ÷ ۱۰۰ = طول کمان مقابل ضلع مربع
میدانیم که بین ضلع مربع و کمان مقابل آن، رابطه زیر برقرار است:
۱/۱۱ ÷ طول کمان = ضلع مربع محاطی
۱/۱۱ ÷ ۲۵ = ضلع مربع محاطی
۲۲/۵۲ = ضلع مربع محاطی
بنابراین، مساحت مربع محاطی به صورت زیر محاسبه میشود:
۲۲/۵۲ × ۲۲/۵۲ = مساحت مربع
۵۰۷/۱۵ = مساحت مربع
در نتیجه، مساحت مربع برابر ۵۰۷/۱۵ سانتیمتر مربع است.
سوالات متداول در رابطه با مساحت مربع داخل دایره
در این بخش، به برخی از سوالات پرتکرار در رابطه با مساحت مربع محاط در دایره به صورت خلاصه پاسخ میدهیم.
مربع محاطی چیست؟
به مربعی که تمام راسهای آن بر روی محیط دایره قرار دارد، مربع محاطی میگویند.
مساحت مربع چگونه بدست میآید؟
مساحت مربع از «ضرب اندازه یک ضلع در خودش» یا «نصف حاصلضرب اندازه قطر در خودش» به دست میآید.
شباهت مربع محاطی با دایره محیطی آن چیست؟
در یک مربع محاطی، اندازه قطر برابر با اندازه قطر دایره محیطی است.
مساحت مربع محاطی چگونه محاسبه میشود؟
مساحت مربع محاطی با استفاده از اندازه قطر دایره محیطی محاسبه میشود.
آیا امکان محاسبه مساحت مربع داخل با اندازههای دیگر دایره وجود دارد؟
بله. در صورت مشخص بودن هر یک از اندازههای دایره، امکان تعیین ضلع، قطر و مساحت مربع فراهم میشود.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مربع — تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مربع چیست ؟ — تعریف و مفاهیم به زبان ساده (+ فیلم آموزش رایگان)
- قطر مربع چیست و چگونه بدست می آید ؟ — به زبان ساده + حل تمرین و مثال
- چگونه محیط مربع را حساب کنیم؟ + فیلم آموزشی و حل تمرین
- مساحت مربع چگونه بدست می آید؟ + فیلم آموزشی و حل تمرین و مثال
- طول ضلع مربع به محیط آن چیست؟ + حل تمرین و مثال
- فرمول محیط مربع چیست ؟ — به زبان ساده + حل تمرین و مثال
- فرمول مساحت مربع چیست ؟ — به زبان ساده + حل تمرین و مثال
- محیط مربع به صورت جبری — فرمول های ریاضی + حل تمرین و مثال
- مساحت مربع به صورت جبری — فرمول های ریاضی + حل تمرین و مثال
- مساحت مربع داخل دایره چگونه بدست می آید ؟ — به زبان ساده + تمرین و مثال(همین مطلب)
- مساحت مربع با قطر چگونه بدست می آید ؟ – به زبان ساده + حل تمرین و مثال











بسیار عالی . ممنونم از سایت خوبتون ?