مجموع زوایای داخلی پنج ضلعی چند درجه است؟ – به زبان ساده

مجموع زاویه های داخلی پنج ضلعی برابر °540 است. این عدد با استفاده از فرمول مجموع زاویه های داخلی n ضلعی بدست می‌آید. در این مقاله از مجله فرادرس، نحوه محاسبه مجموع زوایای داخلی پنج ضلعی های مختلف را به همراه حل چندین مثال متنوع آموزش می‌دهیم. سپس، ضمن توضیح روش استفاده از مثلث برای تعیین مجموع زوایای داخلی، فرمول محاسبه مجموع زوایای خارجی را نیز معرفی می‌کنیم.

چند ضلعی چیست ؟

به هر خط شکسته بسته بر روی یک سطح دو بعدی، چند ضلعی گفته می‌شود. ضلع‌های چند ضلعی، همدیگر را فقط در نقطه اتصال قطع می‌کنند.

تصویر زیر، چند مثال شناخته شده از اشکال هندسی چد ضلعی را نمایش می‌دهد.

زاویه داخلی چیست ؟

به زاویه‌هایی که درون یک چند ضلعی قرار دارند، زاویه‌های داخلی آن چند ضلعی می‌گویند. تصویر زیر، یک هشت ضلعی منتظم و زوایای داخلی را نشان می‌دهد.

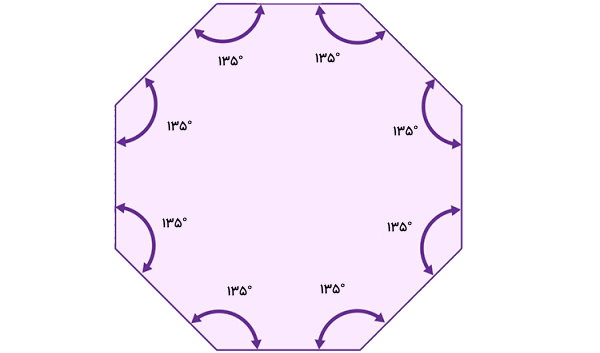
پنج ضلعی چیست ؟

پنج ضلعی، یکی از انواع چند ضلعی است که از پنج ضلع تشکیل می‌شود. این شکل هندسی، پنج زاویه داخلی و پنج زاویه خارجی دارد.

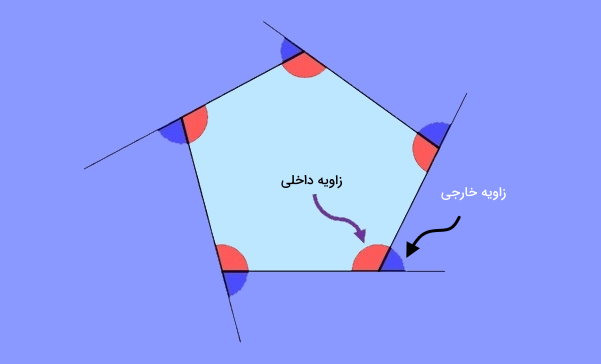
پنج ضلعی منتظم چیست ؟

اگر در یک پنج ضلعی، همه ضلع‌ها با هم و همه زاویه‌ها با هم مساوی باشند، آن پنج ضلعی، منتظم است.

مجموع زوایای داخلی پنج ضلعی چند درجه است؟

مجموع زاویه های داخلی پنج ضلعی، °540 درجه است. این عدد با استفاده از فرمول مجموع زاویه‌های داخلی یک n ضلعی بدست می‌آید.

مجموع زوایای داخلی پنج ضلعی چگونه بدست می آید؟

مجموع زوایای داخلی پنج ضلعی از فرمول زیر محاسبه می‌شود:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی
• n: تعداد ضلع‌ها

این فرمول برای تمام پنج ضلعی‌های منتظم و نامنتظم قابل استفاده است. به منظور محاسبه مجموع زاویه های داخلی پنج ضلعی، تعداد ضلع‌های آن (5) را درون فرمول بالا قرار می‌دهیم:

$$S = (5-2) \times180°$$

$$S = (3) \times 180°$$

$$S = 540°$$

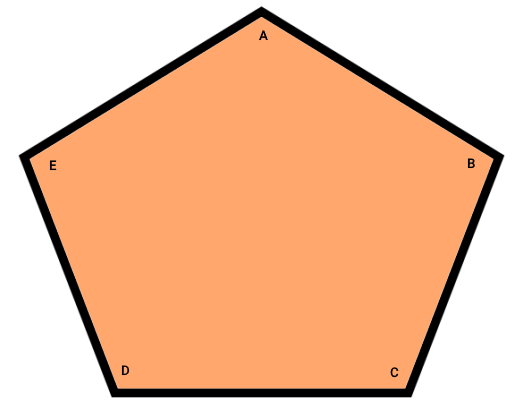
در صورت مشخص بودن تمام زاویه‌های پنج ضلعی و جمع تک به تک مقادیر آن‌ها، عدد به دست آمده برابر 540 درجه می‌شد

540° = زاویه پنجم + زاویه چهارم + زاویه سوم + زاویه دوم + زاویه اول

540° = A + B + C + D + E

مثال 1: محاسبه جمع زاویه های داخلی میز

یک میز چند ضلعی در تصویر زیر نمایش داده شده است. مجموع زوایای داخلی این میز را حساب کنید.

به منظور محاسبه مجموع زاویه های داخلی میز بالا، فرمول زیر را می‌نویسیم:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی میز چند ضلعی
• n: تعداد ضلع‌های میز

میز نمایش داده شده در تصویر، از پنج ضلع تشکیل می‌شود. تعداد این ضلع‌ها (عدد 5) را درون فرمول بالا قرار می‌دهیم و آن را حل می‌کنیم:

$$S = (5-2) \times 180°$$

$$S = (3) \times 180°$$

$$S = 540°$$

در نتیجه، مجموع زوایای داخلی میز برابر 540 درجه است.

مجموع زوایای داخلی پنج ضلعی منتظم چگونه بدست می آید ؟

مجموع زاویه های داخلی پنج ضلعی منتظم با استفاده از فرمول °180×(n-2) به دست می‌آید. بنابراین، مجموع زوایای داخلی این چند ضلعی نیز برابر با 540 درجه است. البته، به دلیل برابر بودن اندازه تمام زوایای داخلی پنج ضلعی منتظم، می‌توان هر یک از زاویه‌های داخلی را توسط فرمول کلی زیر محاسبه کرد:

$$\frac {(n-2) \times 180^{ \circ } } { n }$$

• n: تعداد ضلع‌های چند ضلعی منتظم

مثال 2: تعیین اندازه زاویه داخلی شکل های روی توپ

سطح توپ فوتبال نمایش داده شده در تصویر زیر، از بخش‌های سفید و سیاه تشکیل می‌شود. اگر در بخش‌های سیاه، همه ضلع‌ها با هم و همه زاویه‌ها با هم مساوی باشند:

الف) اندازه هر زاویه چند ضلعی‌های سیاه رنگ چقدر است؟

ب) مجموع زوایای داخلی بخش‌های سفید رنگ چقدر است؟

اگر تعداد ضلع‌های بخش‌های سیاه رنگ توپ را بشماریم، متوجه می‌شویم که این بخش‌ها به شکل پنج ضلعی هستند. به دلیل برابر بودن ضلع‌ها و زاویه‌ها، این پنج ضلعی‌ها، منتظم محسوب می‌شوند. به منظور محاسبه هر زاویه یک پنج ضلعی منتظم می‌توانیم از فرمول زیر استفاده کنیم:

$$\frac {(n-2) \times 180^{ \circ } } { n }$$

• n: تعداد ضلع‌های پنج ضلعی برابر 5

$$\frac {(5-2) \times 180^{ \circ } } { 5 }$$

$$\frac {(3) \times 180^{ \circ } } { 5 }$$

$$\frac {540^{ \circ } } { 5 }$$

$$108^{ \circ }$$

در نتیجه، هر زاویه یک پنج ضلعی منتظم برابر 108 درجه است. برای حل بخش ب مثال، باید فرمول کلی مجموع زوایای داخلی n ضلعی را بنویسیم:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی بخش سفید رنگ توپ
• n: تعداد ضلع‌های بخش سفید رنگ توپ برابر 6

عدد 6 را درون فرمول بالا قرار می‌دهیم و آن را حل می‌کنیم:

$$S = (6-2) \times 180°$$

$$S = (4) \times 180°$$

$$S = 720°$$

در نتیجه، مجموع زوایای داخلی بخش‌های سفید رنگ توپ (شش ضلعی) برابر 720 درجه است.

رابطه بین مجموع زوایای داخلی مثلث و چند ضلعی

مجموع زوایای داخلی یک مثلث برابر 180 درجه است. از این ویژگی می‌توان برای به دست آوردن مجموع زوایای داخلی چند ضلعی‌های دیگر استفاده کرد. به عنوان مثال، هفت ضلعی زیر را در نظر بگیرید.

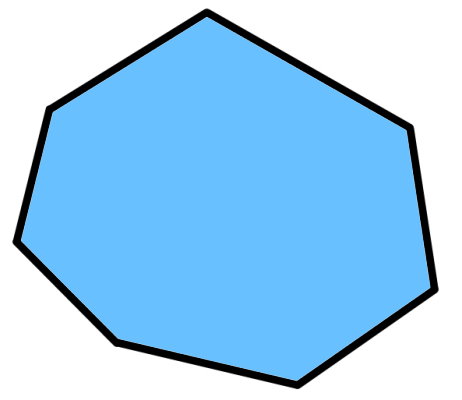
از یکی از راس‌های هفت ضلعی بالا، یک پاره خط به تمام راس‌های دیگر رسم می‌کنیم. اکنون، این هفت ضلعی به پنج مثلث تقسیم می‌شود.

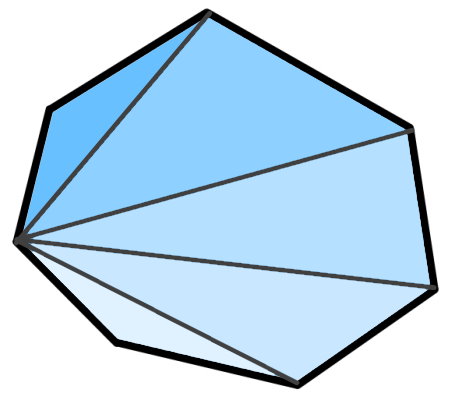
مجموع زوایای داخلی هر یک از مثلث‌های بالا برابر 180 درجه است. به این ترتیب، مجموع زوایای داخلی تمام مثلث‌ها برابر با 900 درجه (جمع تمام زاویه های داخلی مثلث‌ها) خواهد بود.

اگر فرمول مجموع زوایای داخلی هفت ضلعی را بنویسیم و آن را برای n=7 حل کنیم، خواهیم داشت:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی هفت ضلعی
• n: تعداد ضلع‌های هفت ضلعی برابر 7

$$S = (7-2) \times 180°$$

$$S = (5) \times 180°$$

$$S = 900°$$

به عبارت دیگر، مجموع زوایای داخلی یک چند ضلعی، از محاسبه مجموع زوایای داخلی مثلث‌های تشکیل دهنده آن به دست می‌آید. البته این مثلث‌ها باید به روش بالا رسم شوند، تمام سطح چند ضلعی را پوشش دهند و ضلع‌های مثلث‌های دیگر را قطع نکند.

مثال 3: تعیین مجموع زوایای داخلی پنج ضلعی با استفاده از مثلث

مجموع زاویه های داخلی پنج ضلعی زیر را با استفاده از مجموع زوایای داخلی مثلث حساب کنید.

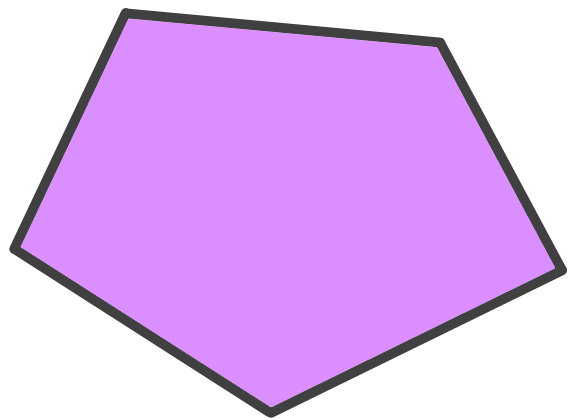
برای شروع، یکی از راس‌های پنج ضلعی (در اینجا C) را انتخاب کرده و از آن به تمام راس‌های دیگر، یک پاره خط رسم می‌کنیم. سپس، تعداد مثلث‌ها را می‌شماریم.

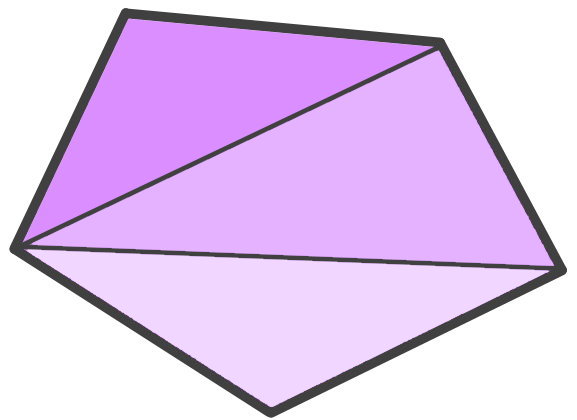
پنج ضلعی بالا به سه مثلث تقسیم شده است. مجموع زوایای داخلی هر مثلث را با هم جمع می‌کنیم:

$$180^{ \circ } + 180^{ \circ } + 180^{ \circ }$$

$$540^{ \circ }$$

مجموع زوایای داخلی سه مثلث برابر با 540 درجه شد. این عدد، مجموع زاویه های داخلی پنج ضلعی است.

مجموع زوایای داخلی پنج ضلعی محدب چگونه بدست می آید ؟

به پنج ضلعی‌هایی که هیچ زاویه بزرگ‌تر از 180 درجه نداشته باشند، پنج ضلعی محدب یا کوژ می‌گویند. تمام پنج ضلعی‌های نشان داده شده در بخش‌های قبلی، محدب بودند. در نتیجه، مجموع زاویه های داخلی پنج ضلعی محدب توسط رابطه زیر به دست می‌آید:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی پنج ضلعی محدب
• n: تعداد ضلع‌های پنج ضلعی محدب برابر 5

$$S = (5-2) \times 180°$$

$$S = (3) \times 180°$$

$$S = 540°$$

مثال 4: رسم چند ضلعی محدب

یک چند ضلعی محدب با مجموع زاویه های داخلی 540 درجه را رسم کنید.

از بین چند ضلعی‌ها، مجموع زاویه های داخلی پنج ضلعی برابر 540 درجه است. بنابراین، این مثال از ما می‌خواهد تا یک پنج ضلعی محدب را رسم کنیم. برای محدب بودن یک پنج ضلعی، هیچ یک از زاویه‌های آن نباید از 180 بیشتر باشد. در نتیجه، می‌توانیم بدون توجه به اندازه دقیق زوایا و ضلع‌ها، شکلی مشابه زیر بکشیم. چراکه در هر صورت، مجموع زاویه‌های این شکل برابر با 540 درجه خواهد بود.

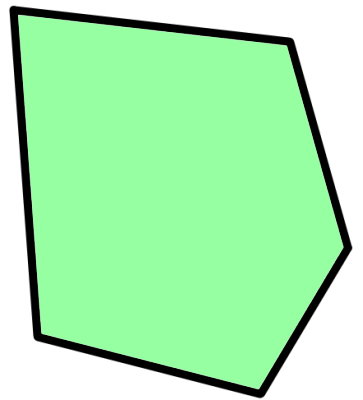
مجموع زوایای داخلی پنج ضلعی مقعر چگونه بدست می آید ؟

به پنج ضلعی‌هایی که دست کم یک زاویه بزرگ‌تر از 180 درجه داشته باشند، پنج ضلعی مقعر یا کاو می‌گویند. تصویر زیر، نمونه‌ای از یک پنج ضلعی مقعر را نمایش می‌دهد.

[]پنج ضلعی مقعر

فرمول مجموع زوایای داخلی پنج ضلعی مقعر عبارت است از:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی پنج ضلعی مقعر
• n: تعداد ضلع‌های پنج ضلعی مقعر برابر 5

همان طور که مشاهده می‌کنید، فرمول مجموع زاویه های پنج ضلعی‌ها در تمام حالت‌ها، با هم برابر است.

مثال 5: مقایسه مجموع زوایای داخلی شکل های منتظم، محدب و مقعر

تصویر زیر، سه چند ضلعی منتظم، محدب و مقعر را نمایش می‌دهد. مجموع زاویه های داخلی هر یک از این چند ضلعی‌ها را با یکدیگر مقایسه کنید.

به منظور تعیین مجموع زوایای داخلی چند ضلعی‌های بالا، ابتدا تعداد ضلع‌‌های آن‌ها را می‌شماریم و یادداشت می‌کنیم:

• چند ضلعی منتظم: 5
• چند ضلعی محدب: 5
• چند ضلعی مقعر: 5

هر سه چند ضلعی دارای پنج ضلع هستند. به عبارت دیگر، تمام این چند ضلعی‌ها، یک نوع پنج ضلعی محسوب می‌شوند. مجموع زوایای داخلی پنج ضلعی نیز از رابطه زیر به دست می‌آید:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی پنج ضلعی
• n: تعداد ضلع‌های پنج ضلعی برابر 5

$$S = (5-2) \times 180°$$

$$S = (3) \times 180°$$

$$S = 540°$$

در نتیجه، مجموع زاویه های داخلی هر کدام از شکل‌ها برابر 540 درجه بوده و با یکدیگر برابر است.

مجموع زوایای خارجی پنج ضلعی چگونه بدست می آید ؟

مجموع زاویه خارجی و داخلی هر یک از راس‌های چند ضلعی‌ها برابر 180 درجه است. با جمع تمام این زوایا (تمام 180 درجه‌ها)، مجموع زاویه های داخلی و خارجی تعیین می‌شود.

فرمول زیر، به منظور محاسبه مجموع زوایای داخلی و خارجی چند ضلعی‌ها مورد استفاده قرار می‌گیرد:

$$S_t = n \times 180°$$

• S_t: مجموع زوایای داخلی و خارجی چند ضلعی
• n: تعداد ضلع‌های چند ضلعی

در صورت کم کردن مجموع زاویه های داخلی چند ضلعی از عدد به دست آمده توسط فرمول بالا، مجموع زوایای خارجی چند ضلعی تعیین می‌شود:

مجموع زوایای داخلی - مجموع زوایای داخلی و خارجی = مجموع زوایای خارجی

مثال 6: تعیین مجموع زوایای خارجی پنج ضلعی

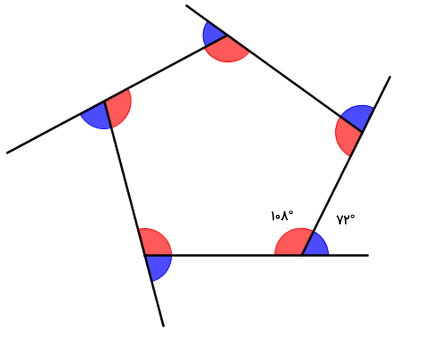
مجموع زوایای خارجی پنج ضلعی منتظم زیر را حساب کنید.

به منظور تعیین مجموع زاویه های خارجی پنج ضلعی، به صورت زیر حساب می‌شود:

مجموع زوایای داخلی - مجموع زوایای داخلی و خارجی = مجموع زوایای خارجی

مجموع زوایای داخلی پنج ضلعی برابر 540 درجه است. به علاوه، مجموع زوایای داخلی و خارجی این شکل از فرمول زیر به دست می‌آید:

$$S_t = n \times 180°$$

• S_t: مجموع زوایای داخلی و خارجی پنج ضلعی
• n: تعداد ضلع‌های پنج ضلعی برابر 5

$$S_t = 5 \times 180°$$

$$S_t = 900°$$

مجموع زاویه های داخلی و خارجی پنج ضلعی برابر با 900 درجه است. در نتیجه:

540° - 900° = مجموع زوایای خارجی پنج ضلعی

360° = مجموع زوایای خارجی پنج ضلعی

مجموع زاویه های خارجی پنج ضلعی برابر 360 درجه است. توجه داشته باشید که مجموع زوایای خارجی برای تمام چند ضلعی‌ها برابر 360 خواهد بود.

سوالات متداول مجموع زاویه های داخلی پنج ضلعی

در این مطلب فهمیدیم مجموع زوایای داخلی پنج ضلعی چند است. در ادامه، به برخی از سوالات متداول در رابطه با مجموع زاویه های داخلی پنج ضلعی پاسخ می‌دهیم.

تعریف پنج ضلعی چیست ؟

پنج ضلعی، یک خط شکسته بسته است که از پنج ضلع تشکیل می‌شود.

مجموع زوایای داخلی پنج ضلعی چقدر است؟

مجموع زاویه های داخلی پنج ضلعی برابر 540 درجه است.

مجموع زوایای داخلی پنج ضلعی منتظم چقدر است؟

مجموع زاویه های داخلی پنج ضلعی منتظم برابر 540 درجه است.

اندازه هر یک از زاویه های داخلی پنج ضلعی منتظم چیست؟

اندازه هر یک از زاویه های داخلی یک پنج ضلعی منتظم برابر 108 درجه است.

مجموع زوایای خارجی پنج ضلعی منتظم چقدر است؟

مجموع زاویه های داخلی پنج ضلعی منتظم برابر 360 درجه است.

اندازه هر یک از زاویه های خارجی پنج ضلعی منتظم چیست؟

اندازه هر یک از زاویه های داخلی یک پنج ضلعی منتظم برابر 72 درجه است.

فرمول مجموع زوایای داخلی چند ضلعی چیست ؟

فرمول مجموع زاویه های داخلی چند ضلعی برابر °180×(n-2) است که در آن، n، تعداد ضلع‌های چند ضلعی را نمایش می‌دهد.