ماتریس در متلب – راهنمای جامع
ماتریس یک آرایه دو بعدی از اعداد است. در این مطلب قصد داریم که با تعریف ماتریس در متلب آشنا شویم و عملیات مختلف روی ماتریسها را در محیط متلب بررسی کنیم.
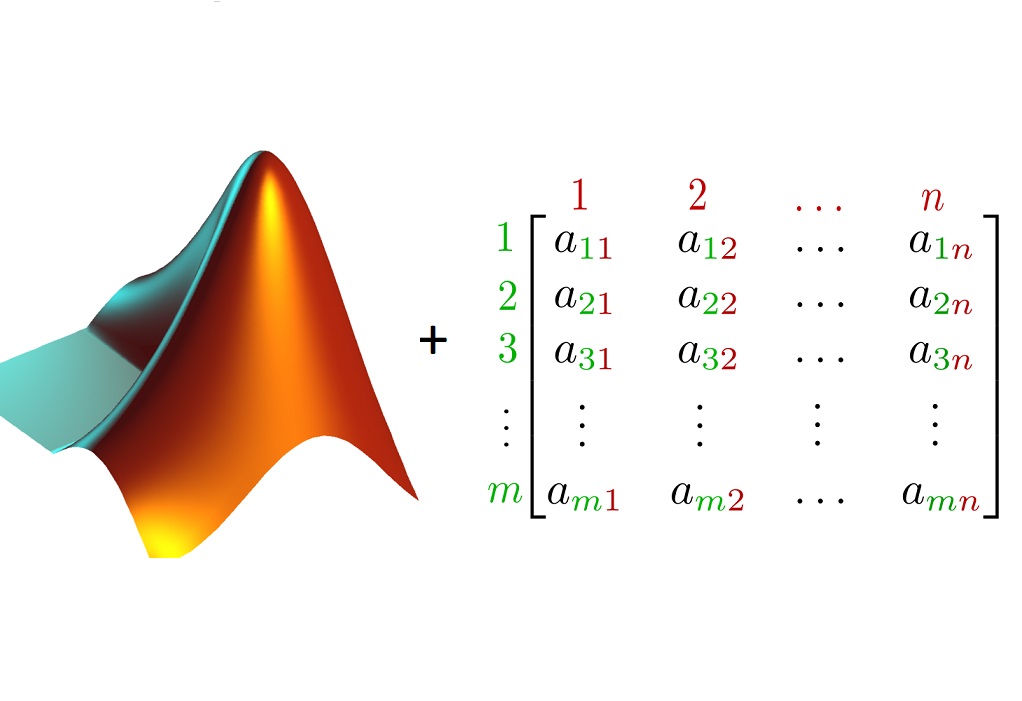
تعریف ماتریس در متلب
برای تعریف یک ماتریس در نرمافزار متلب، میتوان اعداد هر سطر را با علامت تفکیک کننده کاما (,) یا فاصله وارد کرد و سپس برای نشان دادن پایان هر سطر، از علامت نقطه و ویرگول (بدین شکل ) استفاه کرد.
به عنوان مثال میخواهیم یک ماتریس چهار در پنج را در متلب وارد کنیم. برای این کار میتوان به روش زیر عمل کرد.
نرمافزار متلب فرمان بالا را دریافت میکند و در خروجی نتیجه زیر را نمایش میدهد.
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
البته با قرار دادن علامت ; در پایان هر دستور در محیط متلب، میتوان از نمایش حاصل عملیات در خروجی جلوگیری کرد.
برای اشاره کردن به المان موجود در در سطر mام و ستون nام یک ماتریس در متلب (ماتریس فرضی mx) میتوان از دستور زیر استفاده کرد.
مثلا برای به دست آوردن عنصر موجود در سطر ۲ام و ستون ۵ام از ماتریس a که در بخش قبل ایجاد کردیم، باید در محیط نرمافزار متلب، دستور زیر را وارد کنیم.
پس از اجرا شدن، نرمافزار مقدار زیر را در خروجی باز میگرداند.
ans = 6
انتخاب سطر یا ستون از یک ماتریس در متلب
برای اشاره کردن به تمام المانهای موجود در ستون mام از ماتریس a باید به صورت زیر عمل کنیم.
در دستور فوق، m برابر با ۴ قرار داده شده است. پس از اجرا شدن این قطعه کد، نرم افزار متلب نتایج زیر را در خروجی نمایش میدهد.
v =
4
5
6
7
برای اشاره کردن به تمام المانهای موجود در سطر nام از ماتریس a باید قطعه کد زیر را در متلب اجرا کنیم.
در دستور فوق، n برابر با 2 قرار داده شده است. پس از اجرا شدن این قطعه کد، نرم افزار متلب نتیجه زیر را در خروجی نمایش میدهد.
h = 2 3 4 5 6
همچنین میتوان عناصر موجود در ستون mام تا ستون nام را انتخاب کرد. برای این کار میتوان دستور زیر را روی ماتریس a اجرا کرد.
مثلا میتوانیم یک ماتریس کوچکتر را در متلب وارد کنیم و سپس المانهای موجود در ستون دوم و سوم را انتخاب کنیم. بنابراین به طریق زیر عمل میکنیم.
پس از اجرای برنامه، مشاهده میشود که در خروجی مقادیر زیر به دست میآید.
ans =
2 3
3 4
4 5
5 6
به طریق مشابه، میتوان یک زیر-ماتریس ایجاد کرد تا المانهای موجود در بخشی از ماتریس را در خود ذخیره کند.
به عنوان مثال، در قطعه کد زیر، ابتدا ماتریس a را تعریف میکنیم و سپس بخشی از ماتریس را انتخاب کرده و ماتریس جدید b را با استفاه از آن ایجاد میکنیم.
نرمافزار متلب پس از پردازش، نتیجه زیر را در خروجی نمایش میدهد.
b =
2 3
3 4
4 5
5 6
همچنین اگر بخواهیم یک ماتریس ایجاد کنیم که بخش درونی ماتریس a را در خود ذخیره کند، میتوان مجددا به همین روش عمل کرد. مثلا قصد داریم که مقادیر زیر از ماتریس a انتخاب شوند.
3 4 5 4 5 6
بنابراین از قطعه کد زیر استفاده میکنیم و مقادیر فوق را در زیرماتریس sa ذخیره میکنیم.
در خروجی نتیجه به صورت زیر مشاهده میشود.
sa =
3 4 5
4 5 6
پاک کردن سطر یا ستون از یک ماتریس در متلب
در نرمافزار متلب میتوان در صورت نیاز، یک سطر یا ستون را به صورت کامل از یک ماتریس حذف کرد. برای این کار میتوان یک مجموعه تهی (Empty Set) از کروشهها [ ] را به آن سطر یا ستون اختصاص داد؛ زیرا اساسا [ ] نشاندهنده یک آرایه خالی است.
به عنوان مثال میخواهیم سطر چهارم از ماتریس A را پاک کنیم.
نتیجه اجرای کد بالا در نرمافزار متلب به صورت زیر خواهد بود.
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
همان طور که مشاهده میکنید، سطر چهارم از ماتریس a به صورت کامل حذف شده است. به طریق مشابه میتوان ستون پنجم از ماتریس a را نیز پاک کرد.
نتیجه اجرای کد فوق نیز به صورت زیر خواهد بو.د.
a =
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
مثال
برای تفهیم بهتر مطالبی که تا این قسمت بیان شد، در این بخش به ذکر مثالی میپردازیم. میخواهیم یک ماتریس ۳ در ۳ را در نرمافزار متلب ایجاد کنیم و سپس سطر دوم و سوم این ماتریس را انتخاب و آنها را دو بار کپی کنیم تا با استفاده از آنها یک ماتریس جدید با ابعاد ۴ در ۳ به وجود آوریم. برای این کار میتوانیم از قطعه کد زیر استفاده کنیم.
پس از اجرای این برنامه، نتیجه زیر در خروجی نمایش داده میشود.
new_mat =
4 5 6
7 8 9
4 5 6
7 8 9
عملیات روی ماتریس در متلب
در این قسمت میخواهیم عملیات ساده و متداول مورد استفاده روی ماتریسها در متلب را بررسی کنیم.
جمع و تفریق ماتریس در متلب
در محیط نرمافزار متلب میتوان به سادگی ماتریسها را با یکدیگر جمع کرد و یا آنها را از یکدیگر کسر کرد. البته همان طور که میدانیم، برای این کار باید تعداد سطرها و نیز تعداد ستونهای ماتریسها با یکدیگر برابر باشند، به عبارت دیگر، ابعاد ماتریسهایی که با یکدیگر جمع و یا تفریق میشوند باید یکسان باشند. به عنوان مثال، میتوانیم با استفاده از قطعه کد زیر عملیات جمع و تفریق ماتریس در متلب را امتحان کنیم.
زمانی که برنامه فوق را اجرا کنیم، حاصل در خروجی به صورت زیر محاسبه میشود.
c =
8 7 9
6 5 14
12 15 10
d =
-6 -3 -3
2 5 -2
2 1 8
تقسیم ماتریس در متلب
در مورد تقسیم ماتریسها باید بگوییم که ما در واقع ماتریسها را تقسیم نمیکنیم، بلکه به جای تقسیم، از روش زیر استفاده میکنیم:
در عبارت فوق منظور از ، «معکوس ماتریس» B است.
پس ما در واقع ماتریسها را تقسیم نمیکنیم، بلکه به جای آن، ماتریس را در معکوس ماتریس دیگر ضرب میکنیم. اما معکوس ماتریس چیست و چگونه میتوان آن را محاسبه کرد. برای اطلاعات بیشتر در مورد معکوس یک ماتریس میتوانید به مطلب «معکوس ماتریسها – به زبان ساده» مراجعه کنید.
برای تقسیم دو ماتریس در متلب نیز میتوان از یا استفاده کرد. برای عملیات تقسیم دو ماتریس نیز لازم است که ابعاد ماتریسها با یکدیگر برابر باشند. به عنوان مثال، میتوان از قطعه کد زیر برای اجرای تقسیم ماتریسها در متلب استفاده کرد.
نتیجه اجرای این کد به صورت زیر خواهد بود.
c = -0.52542 0.68644 0.66102 -0.42373 0.94068 1.01695 -0.32203 1.19492 1.37288 d = -3.27778 -1.05556 -4.86111 -0.11111 0.11111 -0.27778 3.05556 1.27778 4.30556
عملیات اسکالر روی ماتریس در متلب
اگر یک ماتریس را با یک عدد جمع، تفریق، ضرب و یا تقسیم کنید، آنگاه به این عملیات، عملیات اسکالر میگویند. در عملیات اسکالر، ماتریس نهایی که به دست میآید، دارای تعداد سطر و ستون برابر با ماتریس اولیه است، اما یک عدد ثابت با تمام المانهای ماتریس اولیه جمع، تفریق ضرب و یا تقسیم شده است. به عنوان مثال قطعه کد زیر را در نرمافزار متلب میتوان اجرا کرد. توجه داشته باشید که اسکالر به معنی عدد با ماتریس اسکالر تفاوت داشته و عملیات متفاوتی را ایجاد میکنند.
پس از اجرای برنامه، نتیجه زیر در خروجی نمایش داده میشود.
c =
12 14 25
16 10 8
29 10 11
d =
8 10 21
12 6 4
25 6 7
e =
20 24 46
28 16 12
54 16 18
f =
5.0000 6.0000 11.5000
7.0000 4.0000 3.0000
13.5000 4.0000 4.5000
ترانهاده یک ماتریس در متلب
ترانهاده یک ماتریس (Transpose of a Matrix) عملیاتی است که طی آن سطرها و ستونهای یک ماتریس با یکدیگر عوض میشوند. ترانهاده ماتریس را با علامت نشان میدهند و در متلب نیز از همین نماد برای اعمال ترانهاده استفاده میشود. به عنوان مثال، ترانهاده یک ماتریس فرضی a را با دستور زیر محاسبه میکنیم.
با اجرای قطعه کد فوق، نتیجه زیر در خروجی به دست میآید.
a =
10 12 23
14 8 6
27 8 9
b =
10 14 27
12 8 8
23 6 9
الحاق ماتریس در متلب
میدانیم که دو ماتریس را با هدف ایجاد یک ماتریس بزرگتر، میتوان به یکدیگر الحاق (Concatenate) کرد. برای الحاق ماتریسها به یکدیگر در متلب، میتوان از یک جفت کروشه [ ] استفاه کرد. در متلب، دو نوع الحاق کردن وجود دارد.
- الحاق افقی
- الحاق عمودی
زمانی که دو ماتریس را به یکدیگر الحاق میکنید و در بین آنها از علامت کاما استفاده میکنید، این دو ماتریس به صورت افقی به یکدیگر الحاق میشوند و به این روش الحاق افقی (Horizontal Concatenation) میگویند. به صورت مشابه، زمانی که دو ماتریس را با علامت جداکننده نقطه ویرگول (;) به یکدیگر الحاق میکنید، این روش را الحاق عمودی (Vertical Concatenation) میگویند.
به عنوان مثال، اگر بخواهیم دو ماتریس a و b را به یکدیگر الحاق کنیم، میتوانیم از قطعه کد زیر استفاده کنیم.
در قطعه کد بالا، ماتریس c را با روش الحاق افقی و ماتریس d را با روش الحاق عمودی به دست میآوریم. در خروجی این کد، ماتریسهای a و b و c و d را مشاهده میکنید.
a =
10 12 23
14 8 6
27 8 9
b =
12 31 45
8 0 -9
45 2 11
c =
10 12 23 12 31 45
14 8 6 8 0 -9
27 8 9 45 2 11
d =
10 12 23
14 8 6
27 8 9
12 31 45
8 0 -9
45 2 11
ضرب ماتریس در متلب
دو ماتریس a و b را در نظر بگیرید. اگر a یک ماتریس m * n و b یک ماتریس n * p باشند، آنگاه این دو ماتریس میتوانند در هم ضرب شوند و یک ماتریس m * p ایجاد کنند. البته میدانیم که ضرب دو ماتریس در صورتی امکانپذیر است که تعداد ستونهای ماتریس a یعنی n با تعداد سطرهای ماتریس b برابر باشد. ابعاد ماتریس حاصل ضرب برابر با تعداد سطرهای ماتریس اول در تعداد ستونهای ماتریس دوم است.
برای محاسبه هر المان موجود در موقعیت از ماتریس حاصل ضرب، المانهای سطر i از ماتریس اول را در المانهای متناظر در ستون j از ماتریس دوم ضرب میکنیم و سپس مقادیر حاصل را با یکدیگر جمع میکنیم. برای انجام عمل ضرب دو ماتریس در متلب میتوانیم از * استفاده کنیم. به عنوان مثال، با استفاده از قطعه کد زیر میتوان دو ماتریس a و b را در یکدیگر ضرب کرد.
نتیجه حاصل از اجرای برنامه به صورت زیر خواهد بود.
a =
1 2 3
2 3 4
1 2 5
b =
2 1 3
5 0 -2
2 3 -1
prod =
18 10 -4
27 14 -4
22 16 -6
تعیین دترمینان ماتریس در متلب
برای محاسبه دترمینان یک ماتریس در متلب میتوان از قطعه کد زیر استفاده کرد.
پس از اجرای این برنامه، ماتریس a به همراه دترمینان آن نشان داده میشود.
a =
1 2 3
2 3 4
1 2 5
ans = -2
تعیین دترمینان ماتریس پارامتری در متلب
برای محاسبه دترمینان یک ماتریس پارامتری که برخی آرایهها یا تمام آرایههای آن به صورت یک پارامتر باشند و عدد ثابتی را نمایش ندهند به صورت زیر عمل میکنیم:
با اجرای برنامه خروجی به صورت زیر نمایش داده میشود:
اگر در مثال بالا به جای هر یک از آرایهها عدد ثابتی قرار دهید مجدداً با اجرای دستور det دترمینان ماتریس در خروجی نمایش داده میشود. به عنوان مثال دیگری ماتریس زیر را در نظر بگیرید:
با اجرای دستور det(A) در خروجی دترمینان ماتریس A به صورت زیر نمایش داده میشود:
معکوس ماتریس در متلب
معکوس ماتریس A را با نمایش میدهند. بین یک ماتریس و معکوس آن همواره رابطه زیر برقرار است.
توجه کنید که معکوس ماتریس همیشه برای تمام ماتریسها موجود نیست. اگر دترمینان یک ماتریس برابر با صفر باشد، آنگاه معکوس ماتریس وجود ندارد و ماتریس را تکین (Singular) میگویند. برای محاسبه معکوس یک ماتریس در متلب، میتوان از تابع آماده inv استفاده کرد. به عنوان مثال در قطعه کد زیر، معکوس ماتریس فرضی a با کمک این دستور محاسبه شده است.
نتیجه اجرای این کد نشان دهنده معکوس ماتریس a خواهد بود.
a = 1 2 3 2 3 4 1 2 5 ans = -3.5000 2.0000 0.5000 3.0000 -1.0000 -1.0000 -0.5000 0 0.5000
در این مطلب با نحوه تعریف یک ماتریس در متلب آشنا شدیم و دانستیم که چگونه میتوانیم سطرها و ستونهای خاصی از یک ماتریس را انتخاب کرد و یا عملیات خاص ریاضی را روی ماتریسها انجام داد.
در متنی دیگر به موضوع توان رساندن ماتریسها پرداختهایم. اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های برنامه نویسی
- مجموعه آموزش های برنامهنویسی متلب (MATLAB)
- مجموعه آموزشهای پروژه محور برنامهنویسی
- مجموعه آموزش های برنامهنویسی متلب برای علوم و مهندسی
- منابع آموزشی نرم افزار متلب و برنامه نویسی کاربردی با آن
- تقلب نامه (Cheat Sheet) توابع و دستورات متلب (MATLAB)
- تقلب نامه (Cheat Sheet) تولباکس بهینه سازی در متلب — راهنمای کاربردی
^^













سلام وقتتون بخیر
من یک تصویر دارم به ابعاد 2160 در 2560 و یک فایل اکسل دارم 1080 در 1280 که 4 برابر از تصویر کوچکتر است. من میخواهم هر درایه باهم ضرب بشوند؟ چه راهکاری هستش که این کار رو انجام بدهم؟
سلام خسته نباشید..چجوری میتونم ماتریس های با بیش از ده سطر و ستون در میپل بنویسم؟
سلام در متلب چطور جای سطر اول با ستون آخر و جای سطر دوم با ستون یکی مونده به آخر و…
عوض کنیم؟؟
سلام خسته نباشید . اگه در یکی یا چند تا از درایه ها متغییری مثل s داشته باشیم هم میشه دترمینانش رو محاسبه کرد ؟ چون من متغییر رو تعریف هم کردم باز هم ارور داد .
ممنون
سلام و روز شما به خیر؛
بله این امکان در محاسبات ماتریسی متلب وجود دارد و با توجه به سوال شما مطلب ویرایش شد و بخش «تعیین دترمینان ماتریس پارامتری در متلب» در پاسخ به پرسش شما به متن اضافه گردید.
از اینکه با مجله فرادرس همراه هستید خرسندیم.