قانون هس – به زبان ساده
قانون هس بیان میکند که در یک واکنش شیمیایی، فارغ از مراحل مختلف آن، آنتالپی کل برابر است با مجموع آنتالپی همه تغییرات. به عبارت دیگر، قانون هس به این معناست که آنتالپی، یک «تابع حالت» (State Function) است.

مقدمه
به سبب زحمات ارزنده شیمیدان روسی، «ژرمان هس» (Germain Hess) در خصوص محاسبات ترموشیمی (گرماشیمی)، اولین قوانین و فرمولهای ترموشیمی بیان شدند. قانون هس بواسطه تابع حالت بودن آنتالپی بیان شد که به ما اجازه میدهد برای محاسبه آنتالپی تغییرات کل در یک سیستم، به سادگی تغییرات هر مرحله را با یکدیگر جمع کنیم. هر مرحله باید در یک دمای ثابت انجام شود و معادلات در هر مرحله باید موازنه باشند.
اصلی که قانون هس بر آن بنا شده است تنها برای محسابه آنتالپی کاربرد ندارد بلکه میتوان به منظور محاسبه دیگر توابع حالت مانند تغییر انرژی آزاد گیبس و آنتروپی از آن استفاده کرد.
تعریف قانون هس
(آنتالپی استاندارد تشکیل) برای یک واکنش خاص برابر با مجموع آنتالپیهای هر مرحله از واکنش است.
در بکارگیری این قانون باید در نظر داشته باشیم که تمامی مراحل واکنش باید در یک شرایط انجام شوند.
کاربرد قانون هس
گاز هیدروژن که به عنوان یک سوخت پاک نیز از آن بهره میگیرند، به کمک واکنش کربن (زغال) و آب بوجود میآید:
محاسبات نشان میدهند که برای مصرف هر مول کربن، به میزان گرما نیاز داریم. به طور قراردادی، زمانی که گرما در طول یک واکنش جذب شود، علامت آنرا مثبت در نظر میگیریم. به بیان دیگر، در یک واکنش گرماگیر و در یک واکنش گرماده خواهد بود.
ممکن است این سوال پیش بیاید که چه اتفاقی برای انرژی وارد شده به سیستم خواهد افتاد. یک راه پاسخ این است که بگوییم این انرژی صرف تبدیل یک سوخت (کربن) به سوخت دیگر (هیدروژن) شده است. برای مقایسه انرژی در هر سوخت، میتوانیم گرمای حاصل از احتراق هر سوخت با یک مول از اکسیژن را حساب کنیم:
واکنش بالا در ازای سوختن یک مول از کربن میزان انرژی تولید میکند. بنابراین خواهیم داشت:
همچنین در واکنش زیر، به ازای سوختن دو مول گاز هیدروژن میزان گرما تولید میشود. در نتیجه برای این تغییر شیمیایی خواهیم داشت که معادله آن در زیر آمده است:
انجام محاسبات با قانون هس
مشخص شده است که انرژی بیشتری از سوختن هیدروژن نسبت به سوختن کربن بدست میآید. بنابراین دور از ذهن نیست که تبدیل سوخت کربن به سوخت هیدروژن نیاز به وارد کردن انرژی داشته باشد. واکنش کربن و آب که در بالا مطرح شد را در نظر بگیرید. نکته قابل توجه این است که گرمای گرفته شده برای انجام واکنش که برابر با است، دقیقا برابر با اختلاف گرمای گرفته شده از سوختن کربن و هیدروژن است. این امر تصادفی نیست؛ اگر معادله سوختن کربن را بنویسیم و همچنین عکس واکنش هیدروژن با اکسیژن را به آن اضافه کنیم خواهیم داشت:
میتوانیم را از دو طرف واکنش آخر حذف کنیم چراکه واکنشدهنده و فرآورده نیستند. با حذف از واکنش به همان معادلهای میرسیم که در ابتدای بحث مطرح شد. در نتیجه با استفاده از واکنش سوختن کربن و کم کردن واکنش هیدروژن از آن، به واکنش اول خواهیم رسید:
با مطالعه بسیاری از واکنشهای شیمی به این نتیجه خواهیم رسید که این حالت که به قانون هس معروف است در این واکنشها صدق میکند.

پیشنهاد میکنیم برای درک بهتر این فرمول و مفهوم آن، مطلب جمع بندی فصل دوم شیمی یازدهم را مطالعه کنید.
تعریف تصویری قانون هس
نمایی از قانون هس در تصویر زیر آورده شده است. در این تصویر، واکنشدهندهها در یک کادر قرار داده شدهاند. این کادر بیانگر حالت مواد قبل از واکنش است. فرآوردهها نیز در کادری مجزا حضور دارند.
این کادر دوم بیانگر حالت مواد بعد از واکنش خواهد بود. کادر اول و دوم توسط فلش واکنش و به همراه گرمای آن مرتبط شدهاند. حال تمامی این مواد را در کادر سومی جای میدهیم که شامل ، و خواهد بود. این کادر سوم با فلش واکنش به کادرهای اول و دوم متصل و گرمای واکنش، بالای این فلشها نوشته میشود.
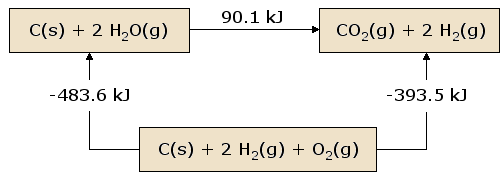
تصویر قانون هس بیان میکند گرمای واکنش در مسیری که به طور مستقیم واکنشدهندهها را به فرآوردهها متصل میکند، دقیقا برابر با مسیر جایگزینی است که در آن مواد واسطه شامل ، و وجود دارند. نتیجه این قانون به ما میگوید که گرمای خالص آزاد شده یا جذب شده به مسیر انجام واکنش وابسته نیست.
در نگاهی دیگر میتوان اینگونه به تصویر نگاه کرد که از کادر اول حرکت کنیم و بعد از عبور از کادر دوم و سوم، دوباره به کادر اول برسیم. در هنگام عبور از کادرها، اعداد گرمای واکنش را با هم جمع میکنیم به این صورت که اگر جهت حرکت با جهت فلش یکسان نبود، علامت آن قرینه میشود، به عبارت بهتر اگر از کادر اول حرکت کنیم، با جمع اعداد خواهیم داشت:
با بررسی رابطه بالا متوجه میشویم گه گرمای خالصِ منتقل شده دقیقا برابر با صفر است. این عبارت به معنای قانون پایستگی انرژی خواهد بود. این قانون بیان میکند که انرژی واکنشدهندهها به فرآیند تولید آنها وابسته نیست. در نتیجه نمیتوانیم از واکنشدهندهها بوسیله فرآیندی که موجب تولید آنها میشود انرژی کسب کنیم.
میتوان تابعی از انرژی توصیف کرد که مقدار آن برای واکنشدهندهها مستقل از نحوه تولید آنها باشد. به همین شکل، این تابع انرژی برای فرآوردهها، مستقل از نحوه تولید آنها خواهد بود. این تابع (ویژگی) را با نام میشناسیم و بنابراین، تغییرات این ویژگی عبارت خواهد بود از:
(واکنش دهندهها) - (فرآوردهها) =
این تغییرات برابر است با گرمای واکنش تحت فشار ثابت. که با نام آنتالپی آن را میشناسند، تابع حالت است، به این معنی که مقدار آن تنها به حالت مواد یعنی دما، فشار و ترکیب مواد بستگی دارد.
مفهوم تابع حالت
مفهوم تابع حالت را میتوان به صورت ساده، با بالا و پایین رفتن از طبقات تشبیه کرد. بالا رفتن از طبقه اول تا سوم را در نظر بگیرید. فرقی نمیکند که ما با آسانسور از طبقه اول به طبقه سوم برویم یا با پله. در هر صورت به طبقه سوم میرسیم. حتی میتوانیم از طبقه اول به طبقه چهارم و بعد از آن به طبقه سوم برسیم. در حقیقت نتیجهای که میگیریم مستقل از مسیر طی شده و به معنای تابع حالت بودن آن است.
بنابراین میتوان یک شرایط استاندارد برای تشکیل هر ماده بیان کرد. این شرایط به این صورت بیان میشود که گرمای دخیل در واکنش را آنتالپی استاندارد تشکیل مینامیم و آن را با نشان میدهیم. این عبارت بیان میکند که واکنش تحت شرایط فشار ثابت اتمسفر انجام شده است.
آنتالپی استاندارد تشکیل
«آنتالپی استاندارد تشکیل» (Standard Enthalpy of Formation) یک ترکیب عبارتست از تغییر آنتالپی به هنگام تشکیل ۱ مول ماده از اجزای سازنده خود که تمامی این مواد در شرایط استاندارد قرار داشته باشند. فشار استاندارد برای این شرایط توسط آیوپاک مقدار در نظر گرفته شده که برابر با است. البته مقدار ۱ اتمسفر که در بالا به آن اشاره شد نیز تا قبل از سال 1982 مورد استفاده قرار میگرفت.
فرمول اصلی برای محاسبه آنتالپی استاندارد تشکیل از رابطه زیر بدست میآید:
در رابطه بالا:
- واژه p نشاندهنده فرآوردهها و r بیانگر واکنشدهندهها است.
- اگر آنگاه واکنش گرماگیر است.
- اگر آنگاه واکنش گرماده است.
حل مسائل آنتالپی سوختن
برای حل مثالهایی که شامل آنتالپی سوختن هستند باید نکات زیر را مد نظر قرار دهید:
- هر معادله را جداگانه موازنه کنید.
- در صورت لزوم به جداول آنتالپیهای استاندارد رجوع کنید.
- در صورت لزوم جهت واکنشها را برعکس کنید تا بتوانید از طرفین برخی عبارات را حذف کنید.
- اگر جهت واکنش را تغییر دادید، علامت واکنش را نیز قرینه کنید.
- در نهایت همه مراحل را با یکدیگر جمع کنید.

مثال
آنتالپی استاندارد حاصل از تبدیل گرافیت به الماس را محاسبه کنید.
واکنشها:
حل:
در مرحله اول، موازنه بودن واکنشها را بررسی و مشاهده میکنیم که هر دو موازنه هستند. آنتالپیهای واکنش داده شدهاند پس نیازی به رجوع به جداول نداریم. همچنین نیازی به معکوس کردن جهت واکنش نیست چراکه از دو طرف میتوان کربن دیاکسید و اکسیژن را خط زد.
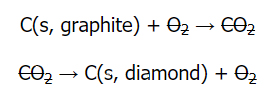
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس شیمی
- مجموعه آموزشهای نرمافزارهای مهندسی شیمی
- آموزش شیمی عمومی
- اصل لوشاتلیه — به زبان ساده
- استوکیومتری — به زبان ساده
^^