فرم جردن در معادلات دیفرانسیل – از صفر تا صد

در مطالب گذشته وبلاگ فرادرس در مورد معادلات دیفرانسیل همگن و ناهمگن بحث شد. هم‌چنین در مطلبی مجزا دستگاه معادلات دیفرانسیل خطی را معرفی کردیم. در این راستا در این مطلب قصد داریم تا روشی تحت عنوان فرم جردن را به منظور حل معادلات دیفرانسیل همگن، توضیح دهیم.

سیستم معادلات دیفرانسیل

به منظور توضیح فرم جردن، در ابتدا سیستمی از $$n$$ معادله دیفرانسیل را به‌صورت زیر در نظر بگیرید.

$$\large \mathbf { X } ’ \left ( t \right ) = A \mathbf { X } \left ( t \right )$$

توجه داشته باشید که عبارت فوق نشان‌دهنده چند معادله دیفرانسیل است. بنابراین فرم ماتریسی این معادلات به‌صورت زیر هستند.

$$ \large { \mathbf { X } \left ( t \right) = \left[ {\begin{array}{*{20}{ c } } { { x _ 1 } \left( t \right ) } \\ { { x _ 2 } \left( t \right ) } \\ \vdots \\ { { x _ n } \left( t \right)} \end {array} } \right],\;\;} \kern-0.3pt { A = \left[ { \begin {array} {*{20} { c } } { { a _ { 11 } } } & { { a _ { 12 } } } & \cdots &{ { a _ { 1 n } } } \\ { { a _ { 21 } } } & { { a _ { 22 } } } & \cdots &{ { a _ { 2n } } } \\ \cdots & \cdots & \cdots & \cdots \\ { { a _ {n 1 } } } & { { a _ { n 2 } } } & \cdots & { { a _{ n n } } } \end {array}} \right] } $$

پاسخی عمومی برای معادلات فوق، باید از $$n$$ تابع خطی مستقل تشکیل شده باشد. زمانی که می‌خواهیم پاسخ معادله را با استفاده از مفهوم بردار ویژه و مقدار ویژه بیابیم، در وهله اول این‌طور به نظر می‌رسد که تعداد بردار‌های ویژه کمتر از $$n$$ است. در چنین مواردی می‌توان با استفاده از مفهوم فرم جردن پاسخی عمومی را برای این مجموعه معادلات حدس زد.

فرم جردن یک ماتریس

فرم جردن یک ماتریس، به حالتی از ماتریس گفته می‌شود که عناصر قرار گرفته روی قطر، ماتریس‌هایی یا بلاک‌هایی مربعی بوده و مابقی عناصر برابر با صفر باشند.

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

توجه داشته باشید که مقادیر ویژه ماتریس‌ها باید روی قطر قرار داشته باشند. مقادیر ویژه $${ \lambda _ i }$$ ممکن است برای یکی از ماتریس‌های روی قطر، برابر باشند. در ادامه شکل کلی یک ماتریس جردن نشان داده شده است.

همان‌طور که در بالا نیز مشاهده می‌کنید، مقادیر نشان داده شده با رنگ‌های یکسان، نشان‌دهنده بلاک‌های ماتریس جردن بوده که روی قطر ماتریس اصلی قرار گرفته‌اند. هم‌چنین توجه داشته باشید که لزومی ندارد تمامی ماتریس‌های قرار گرفته روی قطر، مرتبه‌ای برابر داشته باشند.

بردار‌های ویژه و ماتریس جردن

یک بلاک با مرتبه $$k$$ از یک ماتریس جردن را در نظر بگیرید که مقدار ویژه مرتبط با آن برابر با $$\lambda$$ باشد. این بلاک دارای $$k$$ بردار ویژه است که با $${\mathbf { V } _ 1 } , { \mathbf { V } _ 2 } , { \mathbf { V } _ 3 } , ... , { \mathbf { V } _ k }$$ نام‌گذاری می‌شوند.

بردار $${\mathbf { V } _ 1 }$$، رابطه برداری زیر را ارضا می‌کند. با بدست آمدن $$V _ 1$$، بردار $$V _ 2$$ نیز به‌ صورت زیر بدست خواهد آمد.

$$\large { A { \mathbf { V } _ 1 } = \lambda { \mathbf { V } _ 1 } ,\;\; } \Rightarrow { \left ( { A – \lambda I} \right ) { \mathbf { V } _ 1 } = \mathbf { 0 } }$$

$$\large \left ( { A – \lambda I } \right ) { \mathbf { V } _ 2 } = {\mathbf { V } _ 1 }$$

به بردار فوق،‌ بردار ویژه عمومی‌ شده مرتبه اول گفته می‌شود. به طور مشابه بردار‌های عمومی‌شده مراتب بالاتر را نیز می‌توان به‌صورت زیر بدست آورد.

$$\large \left ( { A – \lambda I } \right ) { \mathbf { V } _ 3 } = { \mathbf { V } _ 2 }$$
$$\ldots \ldots\ldots \ldots \ldots \ldots$$
$$\large \left ( { A – \lambda I } \right ) { \mathbf { V } _ k } = {\mathbf { V } _ { k - 1 } }$$

در ابتدا دو رابطه زیر را در نظر بگیرید.

$$\large { \left ( {A – \lambda I} \right ) { \mathbf { V } _ 1 } = \mathbf { 0 } \;\;\text {and}\;\;} \kern-0.3pt { \left( {A – \lambda I } \right ) { \mathbf { V } _ 2 } = {\mathbf { V } _ 1 } }$$

با ترکیب دو رابطه فوق، معادله زیر بدست خواهد آمد.

$$\large { \left ( { A – \lambda I } \right ) ^ 2 } { \mathbf { V } _ 2 } = \mathbf { 0 }$$

به همین صورت می‌توان برای بردار $$V _ k$$، رابطه زیر را بیان کرد:

$${ \left ( { A – \lambda I } \right ) ^ k } { \mathbf { V } _ k } = \mathbf { 0 }$$

به بردار ویژه $$V _ 1$$ و مجموعه بردار‌های $${ \mathbf { V } _ 2 } , \ldots , \mathbf { V } _ k$$، «زنجیره جردن» (Jordan Chain) گفته می‌شود. توجه داشته باشید که این بردار‌ها به‌صورت خطی نسبت به هم مستقل هستند. هر زنجیره جردنی به طول $$k$$، نشان‌دهنده $$k$$ پاسخ مستقل خطی از یک معادله همگن است. شکل این پاسخ‌ها به‌صورت زیر هستند.

$${ \mathbf { X } _ 1 } = { e ^ { \lambda t } } { \mathbf { V } _ 1 }$$
$${ { \mathbf { X } _ 2 } } = { { e ^ { \lambda t } } \left ( { \frac { t }{ { 1 ! } } { \mathbf { V } _ 1 } + { \mathbf { V } _2 } } \right) }$$
$${ { \mathbf { X } _ 3 } } = { { e ^ { \lambda t } } \left ( { \frac { { { t ^2 } } } { { 2! } } { \mathbf { V } _ 1 } + \frac { t } { { 1! } }{\mathbf { V } _ 2 } + { \mathbf { V } _ 3 } } \right ) }$$
$$\ldots \ldots \ldots\ldots\ldots \ldots\ldots \ldots \ldots \ldots$$
$${ { \mathbf { X } _ k } } = { { e ^ { \lambda t}}\left( {\frac{{{t^{k – 1 } } } } { { \left ( { k – 1 } \right ) ! } } { \mathbf{V}_1} + \cdots }\right.} + { \left.{ \frac { t } { { 1 ! } } { \mathbf { V } _{ k – 1 } } + {\mathbf { V } _ k } } \right ) }$$

تعداد پاسخ‌ها برابر با مجموع طول زنجیر‌های هر بلاک هستند. مجموعه طول تمامی این زنجیر‌ها برابر با $$n$$ یا همان مرتبه ماتریس است. این توابع مستقل خطی، مجموعه پاسخ‌های معادله همگن را تشکیل می‌دهند.

پاسخ عمومی ماتریس‌های $$\large 2 × 2 \ , \ 3 × 3$$

معمولا سیستم‌های معادلات دیفرانسیل که با آن‌ها مواجه هستیم از مرتبه ۲ یا ۳ هستند.

فیلم آموزش ساختارهای جبری، گراف ها و ماتریس ها در فرادرس

کلیک کنید

در این قسمت می‌خواهیم این نمونه از معادلات دیفرانسیل را با استفاده از مفهوم فرم جردن بیابیم. برای این سیستم‌ها در حالت کلی ۸ وضعیت می‌تواند وجود داشته باشد. در جدول زیر این وضعیت‌ها ارائه شده‌اند.

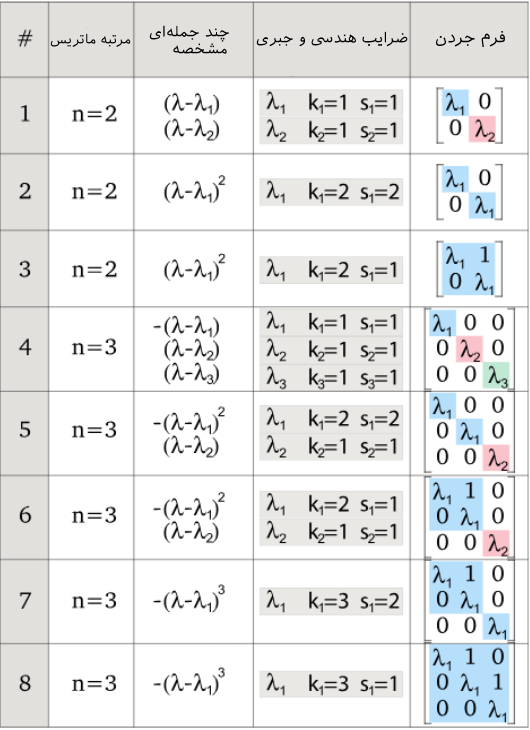
در ادامه در مورد نحوه بدست آوردن بردار‌های ویژه و بردار‌های ویژه عمومی شده بحث خواهیم کرد. ‌هم‌چنین نهایتا پاسخ عمومی را بدست خواهیم آورد.

حالت اول: ماتریس $$2×2$$ و دو مقدار ویژه متفاوتِ $$\lambda_1$$ و $$\lambda_2$$

در این حالت فرم نرمال جردن به‌صورت قطری خواهد بود. هر مقدار ویژه $${ \lambda _ i }$$ دارای یک بردار ویژه $${ \mathbf { V } _ i }$$ است. توجه داشته باشید که این بردار ویژه را می‌توان با حل معادله زیر بر حسب $${ \mathbf { V } _ i }$$، بدست آورد.

$$\large \left ( { A – { \lambda _ i } I } \right ) { \mathbf { V } _ i } = \mathbf { 0 }$$

در نتیجه پاسخ عمومی نیز به‌صورت زیر بدست خواهد آمد.

$$\large { \mathbf { X } \left ( t \right) } = { { C _ 1 } { e ^ { { \lambda _1 } t } } { \mathbf { V } _ 1 } + { C _ 2 } { e ^ { { \lambda _ 2 } t } } {\mathbf { V }_ 2 } }$$

حالت دوم: ماتریس $$2×2$$ و یک مقدار ویژه $$\lambda_1$$ ($$k _ 1=2,s _ 1=2$$)

این ماتریس دارای یک مقدار ویژه $$\lambda _ 2$$ با تکرار‌پذیری $$2$$ است. مرتبه ماتریس برای مقدار ویژه $$\lambda _1$$ برابر با صفر است. بنابراین تکرارپذیری هندسی برابر است با:

$${ {s _ 1 } }={ n – \text {rank} \left ( { A – { \lambda _1 } I } \right) } = { 2 – 0 = 2 }$$

بنابراین پاسخ معادله برداری زیر دو بردارِ مستقلِ $$V _ 1$$ و $$V _ 2$$ هستند. پاسخ عمومی بدست آمده در نتیجه این بردار‌ها برابرند با:

$$\large { \mathbf { X } \left( t \right) }={ { C _ 1 } {e ^ { { \lambda _ 1 } t } } { \mathbf { V } _ 1 } + { C _ 2 } { e ^ { { \lambda _ 1 } t } } { \mathbf { V } _ 2 } }$$

حالت سوم: ماتریس $$2 × 2$$ با $$1$$ مقدار ویژه ($$k_1 = 2 \ , \ s_1 = 1$$)

همانند حالت قبل با محاسبه در خواهیم یافت که مرتبه ماتریس برابر با $$1$$ است. بنابراین تکرار‌پذیری هندسی مقدار ویژه $${ \lambda _ 1 }$$ و تعداد بردار‌های ویژه با هم برابر خواهند بود.

$$\large { { s _ 1 } } = { n – \text {rank} \left ( { A – { \lambda _ 1 } I } \right ) } = { 2 – 1 = 1 }$$

بردار ویژه $${ \mathbf { V } _ 1 } = { \left ( { { V _{ 1 1 } } , { V _ { 21 } } } \right ) ^ T }$$ را می‌توان با استفاده از معادله زیر نیز تعیین کرد.

$$\large \left ( { A – { \lambda _ 1 } I } \right ) { \mathbf { V } _ 1 } = \mathbf { 0 }$$

ماتریس $$H$$ را می‌توان به‌صورت زیر تشکیل داد.

$$ \large H = \left[ {\begin{array} {*{20} { c } }<br /> { { V _ { 11 } } } & { { V _ { 12 } } } \\ { { V _ { 21 } } } & { { V_ { 22 } } } \end {array}} \right] $$

بنابراین فرم جردنِ $$J$$ را می‌توان به‌صورت زیر بدست آورد.

$$\large { H ^ { – 1 } } A H = J$$

در رابطه فوق $$H ^ { - 1 }$$ نشان‌دهنده معکوس ماتریس $$H$$ است. از این ویژگی می‌توان به‌منظور اعتبار‌سنجی بردار‌های ویژه استفاده کرد. نهایتا پاسخ عمومی در این حالت برابر است با:

$$\large { \mathbf { X } \left( t \right) } = { {C_1}{e^{{\lambda _1 } t } } { \mathbf { V } _ 1 } } + { { C _2 } { e ^ { { \lambda _ 1 } t } } \left( { t { \mathbf { V } _ 1 } + { \mathbf { V } _ 2 } } \right ) }$$

حالت چهارم: ماتریس $$3 × 3$$ با $$3$$ مقدار ویژه متفاوتِ $$\lambda _ 1 \ , \ \lambda _ 2 \ , \ \lambda _ 3$$

در این حالت ماتریس جردن به‌صورت قطری است. هر مقدار ویژه $$\lambda _ i$$، بردار ویژه مخصوص به‌ خودش یا همان $${ \mathbf { V } _ i }$$ را خواهد داشت. بدیهی است که این بردار‌های ویژه نیز با استفاده از معادله زیر بدست می‌آیند.

$$\left ( { A – { \lambda _ i } I } \right ) { \mathbf { V } _ i } = \mathbf { 0 }$$

در این حالت پاسخ معادله دیفرانسیل همگن به‌صورت زیر در نظر گرفته می‌شود.

$${ \mathbf { X } \left( t \right) }={ {C_1}{e^{{\lambda _1}t}}{ \mathbf { V } _ 1 } }+{ { C _ 2} { e ^ { { \lambda _ 2 } t } } {\mathbf { V }_ 2 } } + { { C _ 3 } { e ^ { { \lambda _3 } t } }{ \mathbf { V } _ 3 } }$$

حالت پنجم: ماتریس $$3 × 3$$ با $$2$$ مقدار ویژه متفاوتِ $$\lambda _1 ( k _ 1 = 2 , s _ 1 = 2 ) , \lambda _ 2 ( k _ 2 = 1 , s _ 2 = 1 )$$

در این حالت معادله مشخصه دارای دو ریشه با تکرارپذیری $$k _ 1 = 2$$ است. اگر با استفاده از ریشه تکراری $$\lambda _ 1$$ ماتریس $$A – { \lambda _ 1 } I$$ را تشکیل دهیم، در این صورت مرتبه این ماتریس برابر با $$1$$ خواهد بود. در نتیجه تکرارپذیری هندسی $$λ _ 1$$ و تعداد بردار‌های ویژه مرتبط با آن برابرند با:

$${ { s _ 1 } } = { n – \text {rank} \left ( { A – { \lambda _ 1 } I } \right ) } = { 3 – 1 = 2 }$$

هر دو بردار ویژه مستقلِ $${ \mathbf { V } _ 1 }$$ و $${ \mathbf { V } _ 2 }$$ با استفاده از معادله زیر قابل تعیین می‌شوند.

$$\left ( { A – { \lambda _ 1 } I } \right ) { \mathbf { V } } = \mathbf { 0 }$$

بلاک سومِ ماتریس جردن تنها از $$1$$ مقدار ویژه یا همان $$λ_2 ( k _ 2 = 1 , s _ 2 = 1 )$$ تشکیل شده است. بردار ویژه $${ \mathbf { V } _ 3 }$$ نیز با استفاده از معادله زیر بدست خواهد آمد.

$$\large ( A − λ _ 2 I ) V _ 3 = 0$$

در نتیجه پاسخ عمومی معادله دیفرانسیل در این حالت برابر است با:

$${ \mathbf { X } \left( t \right) }={ {C_1}{e^{{\lambda _1}t}} { \mathbf { V } _ 1 } } + { { C _ 2 } { e ^ { { \lambda _ 1 } t } }{ \mathbf { V } _ 2 } } + { { C _ 3 } { e ^ { { \lambda _ 2 } t } } { \mathbf { V } _ 3 } }$$

حالت ششم: ماتریس $$3 × 3$$ با $$2$$ مقدار ویژه متفاوتِ $$\lambda _1 ( k _ 1 = 2 , s _ 1 = 1 ) , \lambda _ 2 ( k _ 2 = 1 , s _ 2 = 1 )$$

این حالت نسبت به حالت قبلی متفاوت بوده و بردار ویژه و مقدار ویژه اول آن متفاوت هستند ($$\lambda _1 , \mathbf { V } _ 1$$). این دو مقدار در رابطه زیر صدق می‌کنند.

$$\left( {A – {\lambda _1}I} \right){\mathbf{V}_1} = \mathbf{0}$$

فیلم آموزش جبر خطی – مرور و حل مساله در فرادرس

کلیک کنید

مرتبه ماتریس به ازای مقدار $$\lambda _ 1$$ برابر با $$2$$ است. بنابراین $$s$$ برابر است با:

$$\large {\text {rank} \left ( { A – { \lambda _1 } I } \right) = 2 } \Rightarrow { { { s _ 1 } } = { n – \text {rank}\left( {A – {\lambda _1 } I } \right ) } = { 3 – 2 = 1 } }$$

بردار مستقل خطی نیز به‌صورت زیر بدست می‌آید.

$$\large \left ( { A – {\lambda _1 } I } \right ) { \mathbf { V } _ 2 } = { \mathbf { V } _ 1 }$$

مقدار ویژه دوم یا $$\lambda_2$$ (مقدار ویژه مربوط به بلاک دوم ماتریس جردن) نیز منجر به ایجاد یک بردارِ ویژه اضافه یا همان $$\mathbf { V _ 3 }$$ خواهد شد. در نتیجه نهایتا پاسخ عمومی برابر است با:

$$ \require{AMSmath.js} { \mathbf { X } \left( t \right) \text{ = }}\kern0pt{ \underbrace { { C _ 1 } { e ^ { { \lambda _1 } t } }{\mathbf { V } _1} + { C _ 2} { e ^ { {\lambda _ 1 } t } } \left( { t { \mathbf { V } _ 1 } + {\mathbf { V }_ 2 } } \right ) } _ { \substack{<br /> \text {1st Jordan block } } } } + { \underbrace { { C _ 3} { e ^ {{ \lambda _ 2 } t } } { \mathbf { V } _3 } } _ { \substack { \text{2nd Jordan block } } } } $$

حالت هفتم: ماتریس $$3 × 3$$ با $$1$$ مقدار ویژه $$λ_1 ( k_1 = 3 , s_1 = 2 )$$

در این حالت ماتریس جردن دارای دو بلاک با یک مقدار ویژه است. بلاک اول دارای یک بردار ویژه $${ \mathbf { V } _ 1 }$$ بوده و یک بردار ویژه عمومی شده $${ \mathbf { V } _ 2 }$$ است. این بردار‌های ویژه را می‌توان با استفاده از دو رابطه زیر بدست آورد.

$$\large {\left( {A – {\lambda _1}I} \right){\mathbf{V}_1} = \mathbf{0},\;\;} \kern-0.3pt {\left ( { A – {\lambda _1}I} \right){\mathbf { V } _ 2 } = {\mathbf { V } _ 1} }$$

معادله اول دارای دو پاسخ برای بردار‌های ویژه است. در حقیقت بردار ویژه دوم، مربوط به بلاک دوم ماتریس جردن است. پاسخ عمومی را می‌توان مطابق با رابطه زیر بیان کرد:

$$\large { \mathbf { X } \left( t \right) \text{ = }}\kern0pt{ \underbrace { { C _ 1} { e ^ { { \lambda _1}t}}{\mathbf{V}_1} + { C _ 2 } { e ^ { { \lambda _ 1 } t } } \left ( { t { \mathbf{V}_1} + {\mathbf { V }_ 2 } } \right) } _ { \substack { \text {1st Jordan block }‌ } } } + { \underbrace { { C _3 } { e ^ { { \lambda _1 } t } } { \mathbf { V } _ 3 } } _ { \substack { \text {2nd Jordan block } } } }$$

حالت هشتم: ماتریس $$3 × 3$$ با $$1$$ مقدار ویژه $$λ_1 ( k_1 = 3 , s_1 = ۱ )$$

در این حالت، اوپراتور خطی $$A$$ دارای یک مقدارِ $${ \lambda _1 }$$ با تکرار‌پذیری $$k_1=3$$ است. مرتبه ماتریسِ $$\left ( { A – { \lambda _ 1 } I } \right )$$ برابر با $$2$$ است. هم‌چنین مرتبه ماتریسِ $$\left ( { A – { \lambda _ 1 } I } \right )$$ نیز برابر با $$2$$ است. بنابراین معادله زیر تنها یک بردار ویژه‌ی $${ \mathbf { V } _ 1 }$$ را خواهد داشت. دو بردار مستقل دیگر را می‌توان با استفاده از دو معادله زیر بدست آورد.

$$\large \begin {gather*} { \left ( { A – { \lambda _ 1 } I } \right ) { \mathbf { V } _ 2 } = {\mathbf { V } _ 1 } ,\;\;} \kern-0.3pt { \left( { A – { \lambda _ 1 } I } \right ) { \mathbf { V } _ 3 } = { \mathbf { V } _ 2 } } \end {gather*}$$

در نتیجه پاسخ عمومی برابر است با:

$$\large { \mathbf { X } \left( t \right) }={ {C_1 } { e^ { {\lambda _1}t}}{ \mathbf{V}_1} } + { {C _ 2} { e ^ { { \lambda _ 1 } t } } \left( {t{\mathbf { V } _ 1 } + { \mathbf{V}_2}} \right) } + { { C _ 3 } { e ^ { { \lambda _ 1 } t } } \left( {\frac { { { t ^2 } } }{ { 2 ! } } { \mathbf { V } _ 1 } + t { \mathbf { V } _2 } + {\mathbf { V} _ 3 } } \right) }$$

در آینده و در مطلبی مجزا مثال‌هایی را از حالت‌های ارائه شده در بالا، ارائه خواهیم داد.