آموزش پیاده سازی شبکه عصبی RBF در پایتون — راهنمای کاربردی

شبکه عصبی RBF یا همان «شبکه عصبی شعاعی پایه» (شبکه Radial Basis Function) نوع رایجی از شبکه‌های عصبی مصنوعی به حساب می‌آید که برای مسائل تقریب تابع (Function Approximation) مورد استفاده قرار می‌گیرد.

شبکه عصبی RBF چیست ؟

شبکه‌های عصبی RBF که کوتاه شده عبارت «Radial Basis Function» (تابع شعاعی پایه) هستند، گونه‌ای خاص از شبکه‌های عصبی مصنوعی به حساب می‌آیند که مبتنی بر فاصله‌اند و شباهت بین داده‌ها را براساس فاصله می‌سنجند.

فیلم آموزش الگوریتم های بهینه سازی در یادگیری ماشین + پیاده سازی در متلب در فرادرس

کلیک کنید

یک شبکه RBF نوعی از شبکه عصبی مصنوعی شبکه عصبی پیشخور (Feed Forward) است که از سه لایه تشکیل می‌شود. هر یک از این لایه در ادامه فهرست شده‌اند:

• لایه ورودی
• لایه پنهان
• لایه خروجی

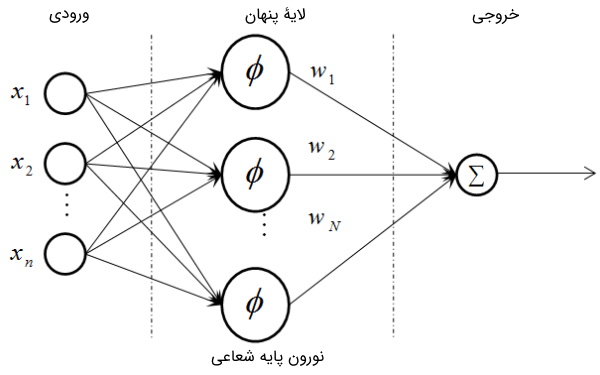
در ادامه مثالی برای درک بهتر فرآیندی ارائه شده است که در شبکه‌های RBF اتفاق می‌افتد.

مثالی برای درک بهتر شبکه عصبی RBF

برای شرح منطق کلی در شبکه‌های عصبی RBF بهتر است مثالی ارائه شود. در این مثال فرض بر این است که ۳ نمونه داده معین وجود دارند و مقادیر ویژگی هدف برای آن‌ها مطابق تصویر زیر است:

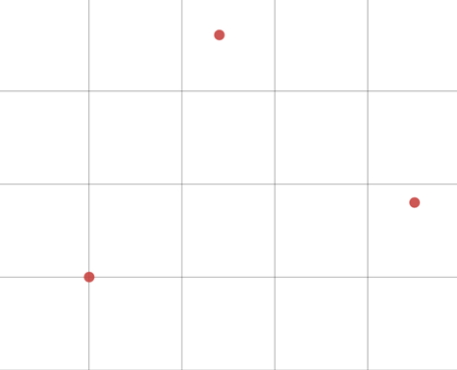
می‌توان برای یک داده ورودی جدید براساس فاصله آن از تک تک داده‌های موجود تصمیم‌گیری کرد. برای مثال داده ورودی جدید در تصویر زیر به صورت علامت ضربدر مشخص شده است:

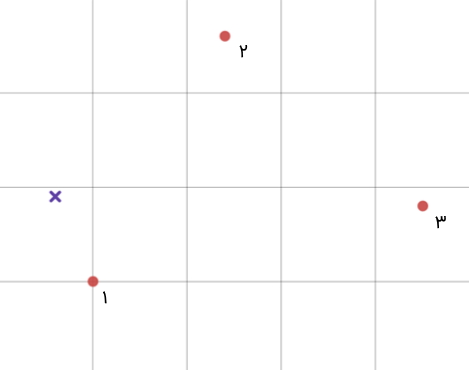
همان‌طور که ملاحظه می‌شود، ورودی جدید به داده شماره یک نزدیک‌تر است؛ بنابراین، ویژگی هدف آن نیز شباهت زیادی به داده شماره یک خواهد داشت. اما اثر داده شماره 2 نیز قابل چشم‌پوشی نیست. در نتیجه بهتر است، عکس فاصله را به عنوان ضریب هر داده نظر گرفت و یک میانگین‌گیری وزن‌دار انجام داد. در شبکه‌های عصبی RBF نیز فرآیندی شبیه به این مثال اتفاق می‌افتد.

فیلم آموزش مقدماتی پیاده سازی شبکه های عصبی مصنوعی در پایتون Python در فرادرس

کلیک کنید

حالا پس از پاسخ به این سوال که شبکه عصبی RBF چیست ، در ادامه می‌توان به بحث اصلی، یعنی پیاده سازی شبکه عصبی RBF در پایتون پرداخت.

پیاده سازی شبکه عصبی RBF در پایتون

در این بخش به آموزش پیاده سازی شبکه عصبی RBF در پایتون پرداخته شده است. هر یک از گام‌های این پیاده سازی در ادامه فهرست شده‌اند:

فیلم آموزش الگوریتم های بهینه سازی در یادگیری ماشین + پیاده سازی در متلب در فرادرس

کلیک کنید

1. فراخوانی کتابخانه‌های مورد نیاز برای پیاده‌سازی شبکه عصبی RBF‌ در پایتون
2. تعیین وضعیت تصادفی و تغییر سبک نمودارها به ggplot
3. ایجاد مجموعه داده مورد نیاز برای پیاده‌سازی شبکه عصبی RBF در پایتون
4. مصورسازی مجموعه داده تولیدی برای پیاده سازی شبکه عصبی RBF در پایتون
5. پیاده‌سازی شبکه عصبی RBF روی مجموعه داده تولید شده در پایتون
6. تعریف تابع fit_wb برای تنظیم بایاس‌های لایه آخر شبکه عصبی RBF در پایتون
7. پیاده‌سازی قانون دلتای تعمیم یافته
8. تعریف تابعی برای سنجش میزان دقت مدل شبکه عصبی RBF در پایتون
9. نحوه مشاهده نموداری روند آموزش مدل شبکه RBF

۱. فراخوانی کتابخانه‌های مورد نیاز برای پیاده‌سازی شبکه عصبی RBF‌ در پایتون

اکنون برای شروع پیاده سازی شبکه عصبی RBF در پایتون ، باید وارد محیط برنامه‌نویسی شده و کتابخانه‌های مورد نیاز را فراخوانی کرد:

1import numpy as np
2import sklearn.cluster as cl
3import sklearn.metrics as met
4import matplotlib.pyplot as plt
5import sklearn.preprocessing as pp

هر یک از کتابخانه‌های فراخوانی شده به ترتیب برای اهداف زیر فراخوانی می‌شوند:

فیلم آموزش مقدماتی پیاده سازی شبکه های عصبی مصنوعی در پایتون Python

کلیک کنید

1. Numpy : کار با آرایه‌ها
2. Sklearn.Cluster : خوشه‌بندی
3. Sklearn.Metrics : محاسبه معیارهای دقت و خطا
4. Matplotlib.Pyplot : رسم نمودار
5. Sklearn.Preprocessing : عملیات پیش‌پردازش

• مقاله‌های پیشنهادی:
  • Scikit-Learn کتابخانه 
  • رسم نمودار در پایتون با Matplotlib — راهنمای کاربردی

۲. تعیین وضعیت تصادفی و تغییر سبک نمودارها به ggplot

ابتدا Random State را تعیین کرده و سپس باید استایل نمودارها را به ggplot تغییر داد:

1np.random.seed(0)
2plt.style.use('ggplot')

حال نیاز به یک مجموعه داده وجود دارد. بنابراین، در ادامه به ایجاد آن در پایتون پرداخته شده است.

۳. ایجاد مجموعه داده مورد نیاز برای پیاده‌سازی شبکه عصبی RBF در پایتون

برای تولید مجموعه داده، نیاز به مجموعه‌‌ای با ۳ دسته مختلف وجود دارد. در این مجموعه داده از توزیع نرمال حول تعدادی مرکز دسته استفاده شده است. ابتدا باید تعداد داده‌ها و مراکز دسته‌ها را مشخص کرد.

فیلم آموزش الگوریتم های بهینه سازی در یادگیری ماشین + پیاده سازی در متلب در فرادرس

کلیک کنید

مشخص کردن تعداد داده‌ها و مراکز دسته‌ها برای ایجاد مجموعه داده

مشخص کردن تعداد داده‌ها و مراکز دسته به صورت زیر انجام می‌شود:

1nD = 200 # Data Size
2M = np.array([[0, 0], [1, 0.6], [0.6, 0.9]]) # Clusters Center
3S = 0.2 # Distribution Variance

در کدهای فوق، 3 مرکز دسته با مختصات (0,0)، (1,0.6) و (0.6,0.9) ایجاد شده‌اند. باید توجه داشت که چون نمایش داده‌هایی با ابعاد بالاتر ممکن نیست، از داده‌های دوبُعدی استفاده شده است. متغیر S نیز برای تعیین انحراف معیار (واریانس) توزیع نرمال تعریف می‌شود که با شدت پراکندگی داده‌ها ارتباط مستقیم دارد. حالا باید تعداد ویژگی‌ها (Features) و تعداد کلاس‌ها (دسته‌ها) را مشخص کرد.

تعیین تعداد ویژگی‌ها و کلاس‌ها برای ایجاد مجموعه داده

تعیین تعداد ویژگی‌ها و کلاس‌ها به صورت زیر انجام می‌شود:

1nC, nX = M.shape

در نتیجه‌ اجرای خط کد بالا، دو متغیر nX و nC به صورت زیر مقداردهی می‌شوند:

$$nC=3$$

$$nX=2$$

ایجاد ماتریس‌های مورد نیاز برای ذخیره‌سازی داده‌ها

حالا باید ماتریس‌هایی خالی را برای ذخیره‌سازی داده‌ها ایجاد کرد:

1X = np.zeros((nD, nX))
2Y = np.zeros((nD, 1))

چون در مسائل دسته‌بندی (Classification) تنها یک ویژگی هدف وجود دارد و آن برچسب (Label) داده است، ماتریس Y تنها دارای یک ستون خواهد بود.

فیلم آموزش الگوریتم های بهینه سازی در یادگیری ماشین + پیاده سازی در متلب در فرادرس

کلیک کنید

تولید و ذخیره‌سازی داده‌ها با استفاده از حلقه For در پایتون

اکنون باید یک حلقه for ایجاد کرد تا به وسیله آن داده‌ها تولید و در ماتریس‌های X و Y ذخیره شوند:

1# Creating Dataset
2for i in range(nD):
3    c = np.random.randint(nC)
4    X[i, :] = M[c] + S*np.random.randn(nX)
5    Y[i, 0] = c

در سطر اول کدهای بالا ابتدا در مورد کلاس داده‌ای که قصد ایجاد آن وجود دارد تصمیم‌گیری شده است که یک عدد از 0 تا 2 خواهد بود. در سطر بعدی، مختصات یک نمونه داده با افزودن مقداری جابه‌جایی (به صورت تصادفی) به مرکز دسته تولید شده است که این میزان جابه‌جایی در تمامی ابعاد به صورت توزیع نرمال خواهد بود. در سطر بعدی نیز برچسب داده‌ها در ماتریس ستونی Y ذخیره می‌شود.

فیلم آموزش مقدماتی پیاده سازی شبکه های عصبی مصنوعی در پایتون Python در فرادرس

کلیک کنید

رمزگذاری ماتریس برچسب‌ها با روش One-Hot

برای انجام مسائل طبقه‌بندی، نیاز است تا ماتریس Y را با روش One-Hot رمزگذاری (Encode) کنیم:

1# One-Hot Encoding Labels
2OHE = pp.OneHotEncoder()
3OHY = OHE.fit_transform(Y).toarray()

اکنون ماتریس OHY تنها شامل اعداد 1 و 0 است و در هر سطر تنها ستون متناظر با کلاس مربوطه، دارای مقدار یک است. توجه داشته باشید که خروجی تابع fit_transform یک آرایه نیست و برای تبدیل آن باید از تابع toarray استفاده شود. پس از اتمام تولید داده‌ها، نیاز است تا آن‌ها را مصورسازی و از مطلوب بودن نتایج اطمینان حاصل کرد.

فیلم آموزش الگوریتم های بهینه سازی در یادگیری ماشین + پیاده سازی در متلب در فرادرس

کلیک کنید

۴. مصورسازی مجموعه داده تولیدی برای پیاده سازی شبکه عصبی RBF در پایتون

مصورسازی داده‌های تولید شده در مرحله قبل به صورت زیر انجام می‌شود:

1# Visualizing Created Data
2plt.scatter(X[:, 0], X[:, 1], c=Y[:, 0], s=20, marker='o')
3plt.scatter(M[:, 0], M[:, 1], c='r', s=80, marker='x', label='Center')
4plt.xlabel('$X_1$')
5plt.ylabel('$X_2$')
6plt.legend()
7plt.show()

عملیات زیر به ترتیب در ۵ سطر فوق انجام می‌شوند:

1. داده‌های تولید شده در محل مختصات خود با رنگ مربوط به دسته خود رسم می‌شوند.
2. مرکزهای دسته‌ها با علامت x و با رنگ قرمز در محل مختصات خود رسم می‌شوند.
3. نام محور افقی به $$X_1$$ تغییر می‌کند.
4. اسم محور عمودی به $$X_2$$ تغییر می‌یابد.
5. برای نمایش برچسب‌ها، legend فراخوانی می‌شود.
6. نمودار نمایش داده خواهد شد.

فیلم آموزش مقدماتی پیاده سازی شبکه های عصبی مصنوعی در پایتون Python در فرادرس

کلیک کنید

در نهایت، خروجی کدهای بالا به صورت زیر خواهد بود:

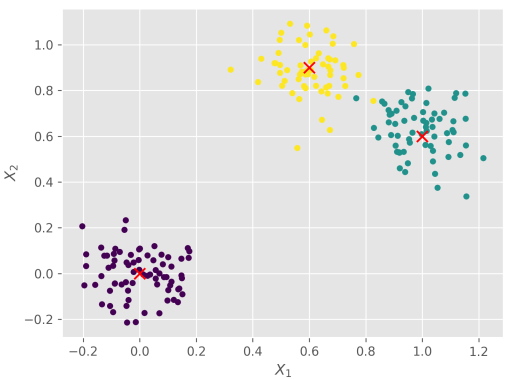
به این ترتیب، مجموعه داده‌ها آماده شده است و می‌توان گام بعدی پیاده سازی شبکه عصبی RBF در پایتون را آغاز کرد. برای ادامه کار باید آشنایی کافی با شبکه‌های عصبی مصنوعی وجود داشته باشد. بنابراین، مطالعه مقاله‌های زیر به آن دسته از افرادی پیشنهاد می‌شود که نیاز به کسب آشنایی با شبکه‌های عصبی مصنوعی دارند:

• انواع شبکه های عصبی مصنوعی — راهنمای جامع
• ساخت شبکه عصبی — راهنمای مقدماتی
• ساخت شبکه عصبی (Neural Network) در پایتون — به زبان ساده
• شبکه عصبی مصنوعی و پیاده‌سازی در پایتون — راهنمای کاربردی
• دسته بندی داده ها با شبکه عصبی مصنوعی | راهنمای کاربردی

۵. پیاده‌سازی شبکه عصبی RBF روی مجموعه داده تولید شده در پایتون

در این بخش هر یک از مراحل پیاده‌سازی شبکه عصبی RBF روی مجموعه داده تولید شده در پایتون شرح داده شده‌اند.

فیلم آموزش الگوریتم های بهینه سازی در یادگیری ماشین + پیاده سازی در متلب در فرادرس

کلیک کنید

ایجاد یک کلاس برای شبکه عصبی RBF

برای پیاده‌سازی شبکه عصبی RBF روی مجموعه داده تولید شده، ابتدا باید یک کلاس برای شبکه عصبی RBF ایجاد شود:

1    Class RBF:

ایجاد تابع سازنده برای پیاده سازی شبکه عصبی RBF در پایتون

سپس باید تابع سازنده را ایجاد کرد:

1    def __init__ (self, name:str):
2        self.name = name

تعریف تابعی برای تعیین مراکز نورون‌ها

حالا باید تابعی برای تعیین مرکزهای نورون‌ها ایجاد شود:

1    def fit_centers (self, X:np.ndarray):
2        self.KMN = cl.KMeans(n_clusters=self.nH)
3        self.KMN.fit(X)
4        self.C = self.KMN.cluster_centers_

این تابع در ورودی ماتریس Xها را می‌گیرد و یک الگوریتم K-Means را روی آن‌ها برازش (Fit) می‌کند. در نهایت نیز باید مراکز خوشه‌ها را با نام C در شی مربوطه ذخیره کرد.

فیلم آموزش الگوریتم های بهینه سازی در یادگیری ماشین + پیاده سازی در متلب در فرادرس

کلیک کنید

• مقاله‌های پیشنهادی:
  • پیاده سازی الگوریتم خوشه بندی K-means در پایتون — راهنمای گام به گام
  • خوشه بندی K-Means در پایتون — راهنمای کاربردی

تعیین تابعی برای برازش جهت اجرای مراحل آموزش مدل

در این مرحله باید تابعی را برای برازش تعیین کرد تا تمامی مراحل آموزش مدل در آن رخ دهند:

1    def fit (self, X:np.ndarray, Y:np.ndarray, nH:int, nEpoch:int=100, lr:float=1e-2):
2        self.nX = X.shape[1]
3        self.nY = Y.shape[1]
4        self.nH = nH
5        self.nEpoch = nEpoch
6        self.lr = lr
7        self.fit_centers(X)
8        self.fit_wb(X, Y)

این تابع در ورودی داده‌ها، تعداد نورون‌های مخفی (مربوط به لایه‌ی RBF)، تعداد مراحل آموزش مدل و نرخ یادگیری را دریافت می‌کند. سپس باید تعداد ورودی، تعداد خروجی، تعداد نورون‌ها، تعداد مراحل آموزش و نرخ یادگیری را در شی مربوطه ذخیره کرد. پس از آن، تابع fit_centers برای تعیین مراکز فراخوانی می‌شود. سپس، تابع fit_wb فراخوانی خواهد شد که این تابع هنوز تعریف نشده است. بنابراین در ادامه به تعریف آن پرداخته می‌شود. پیش از آن به معرفی مجموعه دوره‌های آموزش شبکه‌های عصبی فرادرس پرداخته شده است.

۶. تعریف تابع fit_wb برای تنظیم بایاس‌های لایه آخر شبکه عصبی RBF در پایتون

تابع fit_wb وزن‌ها و بایاس‌های لایه‌ی آخر را تنظیم می‌کند. این تابع به صورت زیر تعریف می‌شود:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):

محاسبه خروجی لایه RBF

ابتدا نیاز است تا خروجی لایه RBF محاسبه شود؛ برای انجام این کار، ابتدا باید فاصله‌ هر داده از هر مرکز را محاسبه کرد. برای انجام این محاسبات از تابع get_distances استفاده شده است:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)

حالا فاصله‌ها باید وارد Basis Function شوند:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)

بدین ترتیب، خروجی لایه اول به دست می‌آید. از این بخش به بعد، می‌توان وزن‌ها و بایاس‌ها را تنظیم کرد. اما ابتدا نیاز است تا مقداردهی اولیه آن‌ها انجام شود.

فیلم آموزش مقدماتی پیاده سازی شبکه های عصبی مصنوعی در پایتون Python در فرادرس

کلیک کنید

مقداردهی اولیه وزن‌ها و بایاس‌ها

مقداردهی اولیه وزن‌ها و بایاس‌ها به صورت زیر انجام می‌شود:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)
4        self.W = np.random.uniform(-1, +1, (self.nH, self.nY))
5        self.B = np.random.uniform(-1, +1, (self.nY))

باید توجه داشت که ماتریس وزن بین لایه مخفی و لایه خروجی تعریف شده است؛ بنابراین شکل آن به صورت $$nH \times nY$$ خواهد بود. ماتریس بایاس نیز تنها برای نورون‌های لایه خروجی تعریف شده و به اندازه خروجی‌های شبکه خواهد بود.

ایجاد یک حلقه برای تک تک Epochها

حالا باید یک حلقه برای تک تک Epochها ایجاد کرد:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)
4        self.W = np.random.uniform(-1, +1, (self.nH, self.nY))
5        self.B = np.random.uniform(-1, +1, (self.nY))
6        for I in range(self.nEpoch):

حال در هر مرحله از آموزش (Train)، برای هر داده باید فرآیند آموزش را تکرار کرد. بنابراین به صورت زیر عمل می‌شود:

1def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)
4        self.W = np.random.uniform(-1, +1, (self.nH, self.nY))
5        self.B = np.random.uniform(-1, +1, (self.nY))
6        for I in range(self.nEpoch):
7            for x, y in zip(O1, Y):

۷. پیاده‌سازی قانون دلتای تعمیم یافته

حال باید قانون GDR یا Generalized Delta Rule (قانون دلتای تعمیم یافته) را پیاده‌سازی کرد.

فیلم آموزش الگوریتم های بهینه سازی در یادگیری ماشین + پیاده سازی در متلب در فرادرس

کلیک کنید

به‌روزرسانی وزن مورد نظر

برای وزن‌ها، دو حلقه تو‌در‌تو نیاز است تا بتوان به ازای هر ورودی و هر خروجی، وزن مورد نظر را به‌روزرسانی کرد:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)
4        self.W = np.random.uniform(-1, +1, (self.nH, self.nY))
5        self.B = np.random.uniform(-1, +1, (self.nY))
6        for I in range(self.nEpoch):
7            for x, y in zip(O1, Y):
8                for j in range(self.nH):
9                    for k in range(self.nY):

محاسبه مقدار خروجی شبکه RBF با استفاده از تابع Model

مقدار خروجی شبکه با استفاده از تابع model به صورت زیر محاسبه می‌شود:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)
4        self.W = np.random.uniform(-1, +1, (self.nH, self.nY))
5        self.B = np.random.uniform(-1, +1, (self.nY))
6        for I in range(self.nEpoch):
7            for x, y in zip(O1, Y):
8                for j in range(self.nH):
9                    for k in range(self.nY):
10                        o = self.model(x)

فرمول قانون GDRبه چه صورت است؟

قانون GDR به صورت زیر است:

$$\Delta W_{i,j} = \eta.x_i.(y_i - o_j).{f'}_{(z)}$$

$$\Delta B_j = \eta.(y_i - o_j).{f'}_{(z)}$$

برای وزن‌ها به صورت زیر خواهیم داشت:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)
4        self.W = np.random.uniform(-1, +1, (self.nH, self.nY))
5        self.B = np.random.uniform(-1, +1, (self.nY))
6        for I in range(self.nEpoch):
7            for x, y in zip(O1, Y):
8                for i in range(self.nH):
9                    for j in range(self.nY):
10                        o = self.model(x)
11                        e = y[j] - o[j]
12                        d = (o[j] * (1 - o[j]))
13                        self.W[i, j] += self.lr * x[i] * e * d

باید توجه داشت که چون از تابع فعال‌سازی Sigmoid در لایه خروجی استفاده خواهد شد، مشتق آن نیز به صورت زیر در خواهد آمد:

$$y = S_{(x)} = \frac{1}{1+e^{-x}} = (1+ e^{-x})^{-1}$$

$$\Rightarrow \frac{dS}{dx} = ((1+e^{-x} )^{-1} )^{'} = -(0-e^{-x}) (1+e^{-x} )^{-2} = \frac {e^{-x}}{(1+e^{-x} )^2} = \frac {e^{-x}}{(1+e^{-x})} S_{(x)}$$

$$\space =(1-S_{(x)} ) S_{(x)} = y(1-y)$$

حالا برای کدهای مربوط به به‌روزرسانی بایاس‌ها نیز می‌توان به روش مشابه عمل کرد:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)
4        self.W = np.random.uniform(-1, +1, (self.nH, self.nY))
5        self.B = np.random.uniform(-1, +1, (self.nY))
6        for I in range(self.nEpoch):
7            for x, y in zip(O1, Y):
8                for i in range(self.nH):
9                    for j in range(self.nY):
10                        o = self.model(x)
11                        e = y[j] - o[j]
12                        d = (o[j] * (1 - o[j]))
13                        self.W[i, j] += self.lr * x[i] * e * d
14                for j in range(self.nY):
15                    o = self.model(x)
16                    e = y[j] - o[j]
17                    d = (o[j] * (1 - o[j]))
18                    self.B[j] += self.lr * e * d

نمایش خطای کلی مدل شبکه عصبی RBF

اکنون تابع کامل شده است. برای اطلاع از شرایط لحظه‌ای مدل، می‌توان در انتهای هر مرحله خطای کلی مدل را به صورت زیر نمایش داد:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)
4        self.W = np.random.uniform(-1, +1, (self.nH, self.nY))
5        self.B = np.random.uniform(-1, +1, (self.nY))
6        O2 = self.model(O1)
7        print(f'Epoch: {0} -- Loss: {round(met.mean_squared_error(Y, O2), 4)}')
8        for I in range(self.nEpoch):
9            for x, y in zip(O1, Y):
10                for i in range(self.nH):
11                    for j in range(self.nY):
12                        o = self.model(x)
13                        e = y[j] - o[j]
14                        d = (o[j] * (1 - o[j]))
15                        self.W[i, j] += self.lr * x[i] * e * d
16                for j in range(self.nY):
17                    o = self.model(x)
18                    e = y[j] - o[j]
19                    d = (o[j] * (1 - o[j]))
20                    self.B[j] += self.lr * e * d
21            O2 = self.model(O1)
22            print(f'Epoch: {I+1} -- Loss: {round(met.mean_squared_error(Y, O2), 4)}')

حال این تابع در ابتدای هر مرحله، مقدار خطای مدل را نیز نمایش خواهد داد. حالا نیاز است تا تابع‌هایی که در طول نوشتن تابع fit_wb از آن‌ها استفاده شده را نیز پیاده‌سازی کرد.

فیلم آموزش الگوریتم های بهینه سازی در یادگیری ماشین + پیاده سازی در متلب در فرادرس

کلیک کنید

کدنویسی تابع محاسبه فاصله (get_distances)

تابع محاسبه فاصله به صورت زیر نوشته می‌شود:

1    def get_distances (self, X:np.ndarray):
2        N = X.shape[0]
3        D = np.zeros((N, self.nH))
4        for i in range(N):
5            for j in range(self.nH):
6                D[i, j] = np.linalg.norm(X[i] - self.C[j], ord=2)
7        return D

این تابع با گرفتن داده‌ها، ابتدا تعداد آن‌ها را در N ذخیره می‌کند. سپس ماتریسی$$N \times nH$$ برای ذخیره فاصله هر داده از هر مرکز ایجاد می‌کند. در نهایت نیز به ازای هر داده و هر مرکز، مقدار Norm محاسبه و ذخیره می‌شود.

پیاده‌سازی تابع bf

در این کد قصد استفاده از تابع گوسی برای این منظور وجود دارد:

1    def bf (self, D:np.ndarray, a:float=10):
2        return np.exp(-a*np.power(D, 2))

در این تابع نیز فرمول ساده شده‌ای از تابع گوسی استفاده شده است. باید توجه داشت که عدد a در تعیین میزان شارپ بودن تابع نقش مهمی دارد و جزء هایپرپارامترهای (فرا پارامترها | Hyperparameter) مسئله محسوب می‌شود.

فیلم آموزش الگوریتم های بهینه سازی در یادگیری ماشین + پیاده سازی در متلب در فرادرس

کلیک کنید

کدنویسی تابع model

کدهای مربوط به این تابع به صورت زیر هستند:

1    def model (self, X:np.ndarray):
2        Z = np.dot(X, self.W) + self.B
3        O = 1/(1 + np.exp(-Z))
4        return O

این تابع ابتدا یک ترکیب خطی از X ایجاد و سپس آن را وارد تابع Sigmoid می‌کند. حال توابع مورد نیاز همگی پیاده‌سازی شده‌اند و برنامه تا به اینجا کامل است.

۸. تعریف تابعی برای سنجش میزان دقت مدل شبکه عصبی RBF در پایتون

برای اینکه بتوان دقت مدل را سنجید، تابعی دیگر برای این منظور به صورت زیر تعریف می‌شود:

1    def accuracy (self, Y:np.ndarray, O:np.ndarray):
2        N = Y.shape[0]
3        a = 0
4        for i in range(N):
5            if np.argmax(Y[i, :]) == np.argmax(O[i, :]):
6                a += 1
7        return a/N

این تابع با دریافت مقادیر هدف و مقادیر پیش‌بینی شده توسط مدل، دقت مدل را بازمی‌گرداند که همواره عددی اعشاری بین 0 و 1 خواهد بود. اکنون باید تابع مورد نظر را در طی مراحل آموزش مدل فراخوانی کرد:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)
4        self.W = np.random.uniform(-1, +1, (self.nH, self.nY))
5        self.B = np.random.uniform(-1, +1, (self.nY))
6        O2 = self.model(O1)
7        E = round(met.mean_squared_error(Y, O2), 4)
8        A = round(self.accuracy(Y, O2), 4)
9        print(f'Epoch: {0} -- Loss: {E} -- Accuracy: {A}')
10        for I in range(self.nEpoch):
11            for x, y in zip(O1, Y):
12                for i in range(self.nH):
13                    for j in range(self.nY):
14                        o = self.model(x)
15                        e = y[j] - o[j]
16                        d = (o[j] * (1 - o[j]))
17                        self.W[i, j] += self.lr * x[i] * e * d
18                for j in range(self.nY):
19                    o = self.model(x)
20                    e = y[j] - o[j]
21                    d = (o[j] * (1 - o[j]))
22                    self.B[j] += self.lr * e * d
23            O2 = self.model(O1)
24            E = round(met.mean_squared_error(Y, O2), 4)
25            A = round(self.accuracy(Y, O2), 4)
26            print(f'Epoch: {I+1} -- Loss: {E} -- Accuracy: {A}')

به این تریتب در طول اجرای برنامه، مرحله، خطا و دقت ملاحظه خواهد شد.

فیلم آموزش الگوریتم های بهینه سازی در یادگیری ماشین + پیاده سازی در متلب در فرادرس

کلیک کنید

ایجاد یک شی با استفاده از داده‌ها و آموزش مدل

حالا با استفاده از کلاس مربوطه یک شی ایجاد کرده و آن شی روی داده‌های مورد نظر آموزش داده خواهد شد:

1Model = RBF('My First RBF')
2
3Model.fit(X, OHY, 3, nEpoch=50, lr=1e-3)

پس از اجرای این کد خواهیم داشت:

Epoch: 0 -- Loss: 0.2025 -- Accuracy: 0.68
.
.
Epoch: 50 -- Loss: 0.1626 -- Accuracy: 0.99

به این صورت، دقت مدل تا مقدار 99 درصد افزایش می‌یابد. تا اینجا شبکه RBF کامل شده است و می‌تواند به خوبی آموزش ببیند. برای اینکه بتوان برای داده‌های جدید نیز خروجی تولید کرد، نیاز است تا تابعی به نام predict تعریف شود:

1    def predict (self, X:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)
4        O2 = self.model(O1)
5        return np.argmax(O2, axis=1).reshape((-1, 1))

تابع Predict شش مرحله کار را روی داده‌های ورودی انجام می‌دهد:

فیلم آموزش مقدماتی پیاده سازی شبکه های عصبی مصنوعی در پایتون Python

کلیک کنید

1. فواصل را محاسبه می‌کند.
2. محاسبه مقدار bf را با توجه به فواصل انجام می‌دهد.
3. یک ترکیب خطی از خروجی لایه RBF ایجاد می‌کند.
4. وارد کردن خروجی ترکیب خطی را به تابع سیگموئید انجام می‌دهد.
5. برای هر داده، نورون برنده با استفاده از تابع argmax تعیین می‌شود.
6. در نهایت نیز ماتریس برنده‌ها را به شکل ستونی در آورده و خروجی می‌دهد.

مقایسه مقدار برچسب با مقدار پیش‌بینی شده به وسیله شبکه RBF

حال می‌توان برای 10 داده اول مقدار برچسب را با مقدار پیش‌بینی شده مقایسه کرد:

1print(Y[:10])
2
3print(Model.predict(X)[:10])

خروجی به صورت زیر خواهد بود:

$$[[0], [1], [2], [1], [0], [0], [0], [2], [1], [0]]$$
$$[[0], [1], [2], [1], [0], [0], [0], [2], [1], [0]]$$

خروجی‌ها برای این 10 داده‌ کاملاً درست هستند.

۹. نحوه مشاهده نموداری روند آموزش مدل شبکه RBF

برای مشاهده روند آموزش مدل به صورت نموداری، می‌توان دقت و خطا را در طول مراحل اجرا ذخیره کرد و در نهایت نمایش داد. برای انجام این کار، تابع fit_wb باید به صورت زیر تغییر داده شود:

1    def fit_wb (self, X:np.ndarray, Y:np.ndarray):
2        D = self.get_distances(X)
3        O1 = self.bf(D)
4        self.W = np.random.uniform(-1, +1, (self.nH, self.nY))
5        self.B = np.random.uniform(-1, +1, (self.nY))
6        self.history = {'loss':[], 'accuracy':[]}
7        O2 = self.model(O1)
8        E = round(met.mean_squared_error(Y, O2), 4)
9        A = round(self.accuracy(Y, O2), 4)
10        self.history['loss'].append(E)
11        self.history['accuracy'].append(A)
12        print(f'Epoch: {0} -- Loss: {E} -- Accuracy: {A}')
13        for I in range(self.nEpoch):
14            for x, y in zip(O1, Y):
15                for i in range(self.nH):
16                    for j in range(self.nY):
17                        o = self.model(x)
18                        e = y[j] - o[j]
19                        d = (o[j] * (1 - o[j]))
20                        self.W[i, j] += self.lr * x[i] * e * d
21                for j in range(self.nY):
22                    o = self.model(x)
23                    e = y[j] - o[j]
24                    d = (o[j] * (1 - o[j]))
25                    self.B[j] += self.lr * e * d
26            O2 = self.model(O1)
27            E = round(met.mean_squared_error(Y, O2), 4)
28            A = round(self.accuracy(Y, O2), 4)
29            self.history['loss'].append(E)
30            self.history['accuracy'].append(A)
31            print(f'Epoch: {I+1} -- Loss: {E} -- Accuracy: {A}')

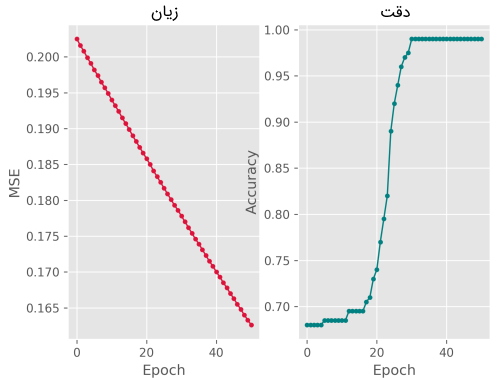
در کدهای فوق یک دیکشتری به اسم history ایجاد می‌شود که دو لیست خالی برای ذخیره خطا و دقت دارد. حال می‌توان این دو نمودار را نمایش داد:

1Losses = Model.history['loss']
2Accuracies = Model.history['accuracy']
3
4plt.subplot(1, 2, 1)
5plt.plot(Losses, lw=1.2, c='crimson', marker='o', ms=3)
6plt.title('Loss')
7plt.xlabel('Epoch')
8plt.ylabel('MSE')
9
10plt.subplot(1, 2, 2)
11plt.plot(Accuracies, lw=1.2, c='teal', marker='o', ms=3)
12plt.title('Accuracy')
13plt.xlabel('Epoch')
14plt.ylabel('Accuracy')
15
16plt.show()

در خروجی این بخش از کد، دو نمودار به صورت زیر حاصل می‌شود:

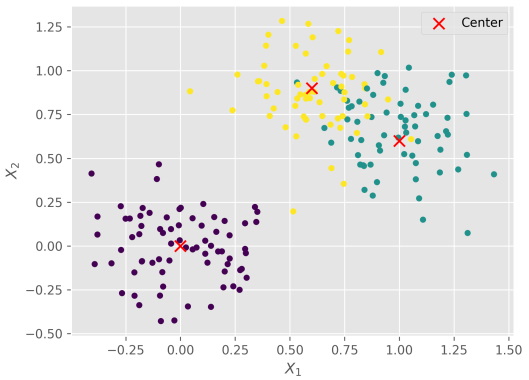
حال اگر شدت پراکندگی را از $$0.1$$ به $$0.2$$ افزایش یابد، نمایش بصری پراکندگی داده به صورت شکل زیر خواهد بود.:

در این صورت، زیان و دقت مدل به شکل زیر است:

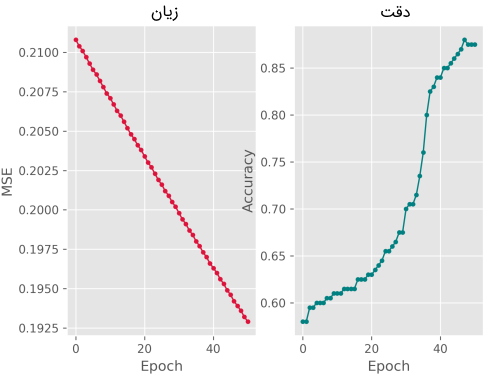
بنابراین به راحتی می‌توان گفت که با درهم‌رفتگی دسته‌ها، دقت مدل نیز کاهش می‌یابد. همچنین، می‌توان دسته‌بندی اصلی را با دسته‌بندی مدل مقایسه کرد:

1O = Model.predict(X)
2
3plt.subplot(1, 2, 1)
4plt.scatter(X[:, 0], X[:, 1], c=Y[:, 0], s=20, marker='o')
5plt.scatter(M[:, 0], M[:, 1], c='r', s=80, marker='x', label='Center')
6plt.title('Real')
7plt.xlabel('$X_1$')
8plt.ylabel('$X_2$')
9plt.legend()
10
11plt.subplot(1, 2, 2)
12plt.scatter(X[:, 0], X[:, 1], c=O[:, 0], s=20, marker='o')
13plt.scatter(M[:, 0], M[:, 1], c='r', s=80, marker='x', label='Center')
14plt.title('Predicted')
15plt.xlabel('$X_1$')
16plt.ylabel('$X_2$')
17plt.legend()
18
19plt.savefig('5.png',dpi=300)

در خروجی این بخش نیز دو نمودار به شکل زیر ایجاد می‌شوند:

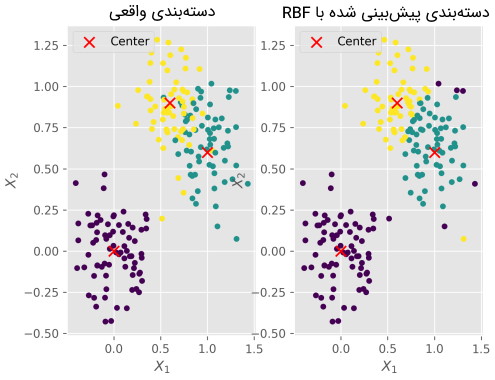
به این ترتیب، آموزش پیاده سازی شبکه عصبی RBF در پایتون به پایان می‌رسد. پیش از ارائه یک جمع‌بندی به م

فیلم مجموعه آموزش شبکه‌ های عصبی مصنوعی – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

جمع‌بندی

در پروژه پیاده سازی شبکه عصبی RBF در پایتون، ابتدا مجموعه داده‌ای ایجاد و سپس با استفاده از مفهوم شی‌گرایی، یک کلاس برای شبکه‌های عصبی RBF تعریف شد که می‌تواند به خوبی عمل طبقه‌بندی را انجام دهد.

فیلم مجموعه آموزش برنامه نویسی پایتون Python – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

برای آزمایش و پژوهش بیش‌تر، می‌توان تعداد کلاس‌ها، تعداد خوشه‌های الگوریتم K-Means، ضریب تابع bf و نرخ یادگیری را تغییر داد و اثر هرکدام را در خروجی ملاحظه کرد.