دستگاه معادلات غیرخطی – به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزش‌های قبلی مجله فرادرس، روش‌های حل دستگاه معادلات خطی را بیان کردیم. موضوع این آموزش، دستگاه معادلات غیرخطی است. دستگاه معادلاتی را غیرخطی می‌گوییم که توان حداقل یکی از متغیرهای مجهول آن، بیشتر از ۱ باشد و یا در معادلات، ضرب بین متغیرهای مجهول وجود داشته باشد.

برای حل این دستگاه معادلات، مانند حل دستگاه معادلات خطی، از روش جانشینی (جایگذاری) یا حذف استفاده می‌کنیم. البته در این‌جا، تفاوت اساسی این است که امکان دارد حل معادلات غیرخطی، مختلط باشد. مثال‌هایی که در ادامه می‌آیند، این موضوع را به‌خوبی نشان می‌دهند.

مثال ۱

دستگاه معادلات زیر را حل کنید:

$$\begin{align*}{x^2} + {y^2} & = 10\\ 2x + y & = 1\end{align*}$$

حل: در دستگاه معادلات خطی می‌توانیم روش حل را انتخاب کنیم، اما در دستگاه معادلات غیرخطی، همیشه حق انتخاب نداریم. در دستگاه بالا، متغیرهای معادله نخست توان دوم دارند و متغیرهای معادله دوم، توانی ندارند. به عبارت دیگر، راهی برای آنکه بتوانیم از روش حذف استفاده کنیم وجود ندارد و مجبوریم از روش جایگذاری استفاده کنیم. خوشبختانه، این اجبار برای این دستگاه خیلی هم بد نیست، زیرا می‌توان به‌سادگی معادله دوم را برحسب $$y$$ بیان کرد و آن را در معادله اول قرار داد.

$$y = 1 - 2x$$

$${x^2} + {\left( {1 - 2x} \right)^2} = 10$$

معادله اخیر، یک معادله درجه دوم با ضرایب ثابت است و به‌سادگی می‌توان آن را حل کرد.

$$\begin{align*}{x^2} + 1 - 4x + 4{x^2} & = 10\\ 5{x^2} - 4x - 9 & = 0\\ \left( {x + 1} \right)\left( {5x - 9} \right) & = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}x = - 1,\,\,x = \frac{9}{5}\end{align*}$$

همان‌طور که می‌بینیم، دو پاسخ برای $$x$$ به‌دست آمده است. در ادامه باید مقدار $$y$$ را تعیین کنیم. برای هر دو مقدار $$x$$، داریم:

$$x = - 1 \hspace{0.25in} \Rightarrow \hspace{0.25in}y = 1 - 2\left( { - 1} \right) = 3$$

$$x = \frac{9}{5}\hspace{0.25in} \Rightarrow \hspace{0.25in}y = 1 - 2\left( {\frac{9}{5}} \right) = - \frac{{13}}{5}$$

می‌بینیم که دستگاه فوق، فقط دو پاسخ دارد. این دو پاسخ، نقاطی را نشان می‌دهند که در آن‌ها، منحنی‌های دو معادله با هم برخورد می‌کند. از آن‌جایی که معادله اول، یک دایره و معادله دوم یک خط راست است، منحنی‌ها در دو نقطه یک‌دیگر را قطع می‌کنند. شکل زیر این موضوع را به‌خوبی نشان می‌دهد.

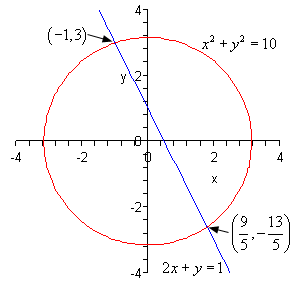
اگه به نمودارهای مربوط به دو معادله دقت کنیم، می‌بینم که سه حالت برای پاسخ دستگاه معادلات وجود دارد که می‌تواند یک نقطه، دو نقطه یا بدون جواب باشد.

مثال ۲

دستگاه معادلات زیر را حل کنید.

$$\begin{align*}{x^2} - 2{y^2} & = 2\\ xy & = 2\end{align*}$$

فیلم آموزش مبانی آنالیز عددی – بخش یکم در فرادرس

کلیک کنید

حل: در این مثال، یک هذلولی (در معادله اول، هرچند به‌فرم استاندارد نیست) و یک تابع کسری (در معادله دوم) داریم. در این مثال نیز ناگزیر به استفاده از روش جایگذاری هستیم.

بهترین راه برای حل دستگاه، حل معادله دوم برای $$x$$ یا $$y$$ است. در این‌جا، $$y$$ را برحسب $$x$$ محاسبه می‌کنیم.

$$y = \frac{2}{x}$$

در نتیجه:

$$\begin{align*}{x^2} - 2{\left( {\frac{2}{x}} \right)^2} & = 2\\ {x^2} - 2\frac{4}{{{x^2}}} & = 2\\ {x^2} - \frac{8}{{{x^2}}} & = 2\end{align*}$$

برای حذف $$x^2$$ از مخرج، دو طرف معادله اخیر را در $$x^2$$ ضرب می‌کنیم. بنابراین، داریم:

$$\begin{align*}{x^4} - 8 & = 2{x^2}\\ {x^4} - 2{x^2} - 8 & = 0\end{align*}$$

اگه به معادله بالا دقت کنیم، می‌توانیم آن را به‌صورت یک معادله درجه دوم بنویسیم. برای این کار، متغیر $$u$$ را به‌صورت زیر تعریف می‌کنیم:

$$u = {x^2}\hspace{0.25in} \Rightarrow \hspace{0.25in}{u^2} = {\left( {{x^2}} \right)^2} = {x^4}$$

در نتیجه، معادله را می‌توان به‌شکل زیر بازنویسی کرد:

$$\begin{align*}{u^2} - 2u - 8 & = 0\\ \left( {u - 4} \right)\left( {u + 2} \right) & = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}u = - 2,\,\,\,u = 4\end{align*}$$

یعنی جواب‌ها برای $$x$$ به‌صورت زیر است:

$$\begin{align*}{x^2} & = 4\hspace{0.25in} \Rightarrow \hspace{0.25in}x = \pm \,2\\ {x^2} & = - 2\hspace{0.25in} \Rightarrow \hspace{0.25in}x = \pm \,\sqrt 2 \,\,i\end{align*}$$

در نتیجه، چهار مقدار ممکن برای $$x$$ وجود دارد که دو مورد آن‌ها مختلط است. برای تعیین $$y$$ می‌توانیم مقادیر $$x$$ را در معادله دوم دستگاه معادلات قرار دهیم:

$$\begin{align*}x & = 2\hspace{0.25in} \Rightarrow \hspace{0.25in}y = \frac{2}{2} = 1\\ x & = - 2\hspace{0.25in} \Rightarrow \hspace{0.25in}y = \frac{2}{{ - 2}} = - 1\end{align*}$$

$$\begin{align*}x & = \sqrt 2 \,i\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}y = \frac{2}{{\sqrt 2 \,i}} = \frac{2}{{\sqrt 2 \,i}}\frac{i}{i} = \frac{{2i}}{{\sqrt 2 \,{i^2}}} = - \frac{{2i}}{{\sqrt 2 }}\\ x & = - \sqrt 2 \,i\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}y = - \frac{2}{{\sqrt 2 \,i}} = - \frac{2}{{\sqrt 2 \,i}}\frac{i}{i} = - \frac{{2i}}{{\sqrt 2 \,{i^2}}} = \frac{{2i}}{{\sqrt 2 }}\end{align*}$$

برای پاسخ‌های مختلط، باید $$i$$ را به صورت کسر منتقل کنیم. در نتیجه، پاسخ‌های نهایی به‌صورت زیر هستند:

$$\begin{align*}& x = 2,\,\,\,y = 1\hspace{0.25in}{\mbox{و}}\hspace{0.25in}x = - 2,y = - 1\hspace{0.25in}{\mbox{و}}\\ & x = \sqrt 2 \,i,\,\,\,y = - \frac{{2i}}{{\sqrt 2 }}\hspace{0.25in}{\mbox{و}}\hspace{0.25in}x = - \sqrt 2 \,i,\,\,\,y = \frac{{2i}}{{\sqrt 2 }}\end{align*}$$

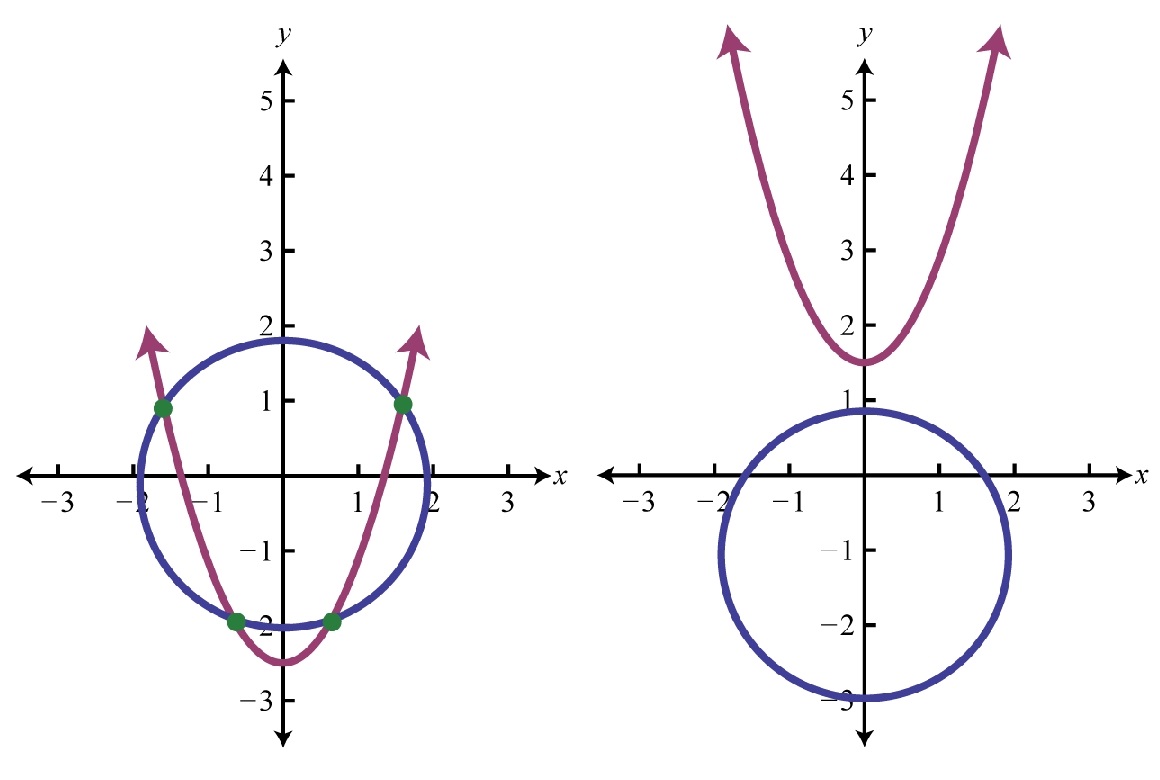
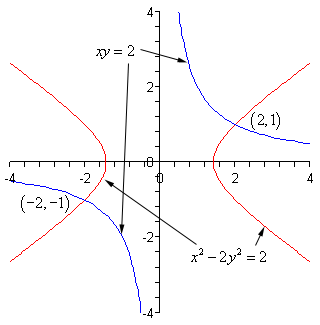
دو مورد از پاسخ‌ها حقیقی هستند و نقاط برخورد منحنی‌های دو معادله را نشان می‌دهند. دو پاسخ دیگر، مختلط هستند و نشتن دهنده نقاط برخورد منحنی‌ها نیستند. نمودار دو معادله به‌شکل زیر است.

مثال ۳

دستگاه معادلات زیر را حل کنید.

$$\begin{align*}2{x^2} + {y^2} & = 24\\ {x^2} - {y^2} & = - 12\end{align*}$$

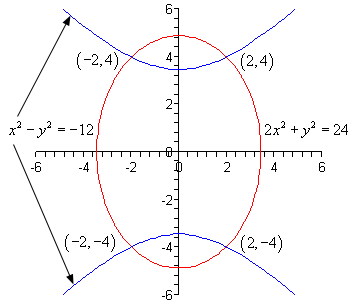
حل: نمودار یکی از معادلات دستگاه بالا، بیضی و دیگری هذلولی است؛ هرچند یکی از آن‌ها به‌فرم استاندارد نیست. در دو مثال قبل نتوانستیم از روش حذفی استفاده کنیم. در این مثال می‌توانیم این کار را انجام دهیم. برای این کار، کافی است دو معادله را با هم جمع کنیم که در این صورت، متغیر $$y$$ حذف خواهد شد.

$$\begin{array}{c} 2{x^2} + {y^2} = 24\\ \underline{ {x^2} - {y^2} = - 12 } \end{array} \\ 3{x^2}\,\,\,\,\,\,\,\,\,\,\,\,\, = 12$$

در نتیجه، مقدار $$x$$ را محاسبه می‌کنیم:

$$\begin{align*}3{x^2} & = 12\\ {x^2} & = 4\hspace{0.25in} \Rightarrow \hspace{0.25in}x = \pm \,2\end{align*}$$

برای تعیین $$y$$ نیز می‌توانیم مقدار به‌دست‌آمده $$x$$ را در یکی از معادلات جایگذاری کنیم. برای مثال، از معادله نخست استفاده می‌کنیم:

اگر $$x=2$$، آن‌گاه:

$$\begin{align*}2{\left( 2 \right)^2} + {y^2} & = 24\\ 8 + {y^2} & = 24\\ {y^2} & = 16\hspace{0.25in} \Rightarrow \hspace{0.25in}y = \pm 4\end{align*}$$

و اگر $$x=-2$$، آن‌گاه:

$$\begin{align*}2{\left( { - 2} \right)^2} + {y^2} & = 24\\ 8 + {y^2} & = 24\\ {y^2} & = 16\hspace{0.25in} \Rightarrow \hspace{0.25in}y = \pm 4\end{align*}$$

در این مثال، برخلاف مثال‌های قبل به‌ازای هر مقدار $$x$$ دو جواب برای $$y$$ خواهیم داشت. این یعنی اینکه دستگاه معادلات دارای چهار جواب زیر است:

$$\left( {2,4} \right)\hspace{0.25in}\left( {2, - 4} \right)\hspace{0.25in}\left( { - 2,4} \right)\,\,\,\,\,\left( { - 2, - 4} \right)$$

چهار نقطه این موضوع را نشان می‌دهند که دو منحنی مربوط به معادلات، در چهار نقطه یک‌دیگر را قطع می‌کنند.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• معادله دیفرانسیل برنولی — از صفر تا صد
• ﻣﻌﺎدﻻت دﯾﻔﺮاﻧﺴﯿﻞ ﺑﺎ ﻣﺸﺘﻘﺎت ﺟﺰﺋﯽ — از صفر تا صد
• معادله خط — به زبان ساده
• دستگاه معادلات دیفرانسیل خطی — به زبان ساده

^^