تطبیق امپدانس – به زبان ساده + مثالهای متنوع

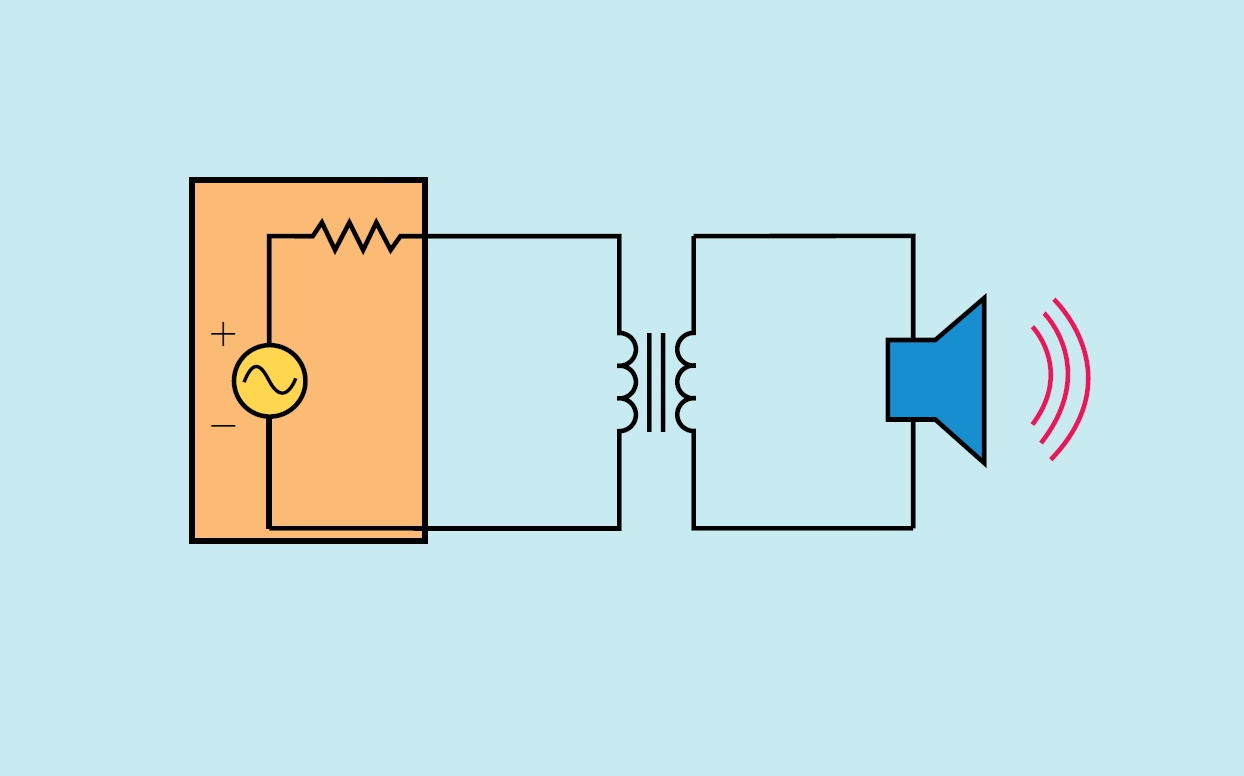
اصطلاح «تطبیق امپدانس» (Impedance Matching) مفهوم ساده‌ای دارد و به زبان ساده، فرایند ایجاد یک امپدانس مشابه امپدانس دیگر است. غالباً در موارد کاربردی لازم است امپدانس بار را با منبع یا امپدانس داخلی یک منبع تطبیق دهیم. طیف گسترده‌ای از قطعات و مدارها را می‌توان برای تطبیق امپدانس استفاده کرد. در این آموزش با تطبیق امپدانس و روش‌های آن آشنا می‌شویم.

تطبیق امپدانس چیست؟

طبق قضیه انتقال توان ماکزیمم، برای انتقال حداکثر مقدار انرژی از یک منبع به یک بار، امپدانس بار باید با امپدانس منبع مطابقت داشته باشد.

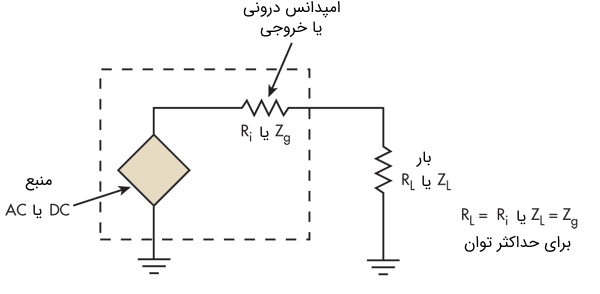
در نظریه مدار، یک منبع می‌تواند dc یا ac باشد و از طریق مقاومت داخلی ($$R_i$$) یا امپدانس خروجی ژنراتور ($$Z_g$$)، مقاومت ($$R_L$$) یا امپدانس ($$Z_L$$) بار را تغذیه کند (شکل ۱).

شکل ۲ نمودار توان بار در مقابل مقاومت بار را نشان می‌دهد که تطبیق امپدانس‌های بار و منبع، به حداکثر توان می‌انجامد (شکل 2).

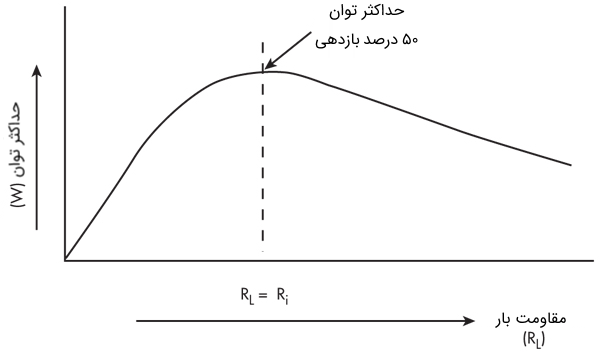
یک عامل کلیدی این قضیه این است که وقتی بار با منبع مطابقت دارد، میزان توان تحویل داده شده به بار، همان توان مصرفی در منبع است. بنابراین، انتقال حداکثر توان تنها ۵۰ درصد بازدهی دارد. برای تحویل حداکثر توان بار، توان ژنراتور باید دو برابر توان خروجی مورد نظر باشد.

کاربردهای تطبیق امپدانس

تطبیق امپدانس کاربردهای زیادی در مهندسی برق دارد که در این بخش چند مورد را بیان می‌کنیم.

فیلم آموزش الکترونیک ۳ – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

تطبیق امپدانس بلندگو و تقویت کننده صوتی

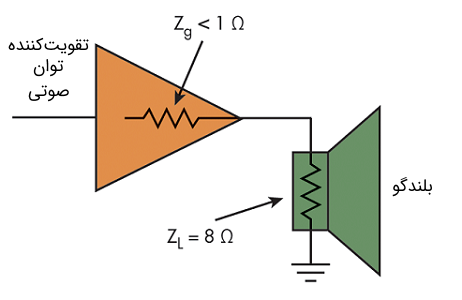
تحویل حداکثر توان از یک منبع به یک بار به طور مکرر در الکترونیک اتفاق می‌افتد. یک مثال این است که بلندگو در یک سیستم صوتی، سیگنالی را از یک تقویت‌کننده (آمپلی‌فایر) توان دریافت می‌کند (شکل ۳). حداکثر توان وقتی تحویل می‌شود که امپدانس بلندگو با امپدانس خروجی تقویت‌کننده توان مطابقت داشته باشد. در حالی که این موضوع از لحاظ نظری صحیح است، معلوم می‌شود که بهترین آرایش این است که امپدانس تقویت‌کننده توان کمتر از امپدانس بلندگو باشد. دلیل این امر پیچیدگی بلندگو به عنوان بار و پاسخ مکانیکی آن است.

تطبیق امپدانس فرستنده

مثال دیگر، انتقال توان از طبقه به طبقه دیگر در فرستنده است (شکل ۴). امپدانس ورودی مختلط $$(R\pm j X)$$ تقویت‌کننده $$B$$ باید با امپدانس خروجی مختلط تقویت‌کننده $$A$$ مطابقت داشته باشد. این موضوع بسیار مهم است که اجزای راکتیو یکدیگر را خنثی یا حذف کنند.

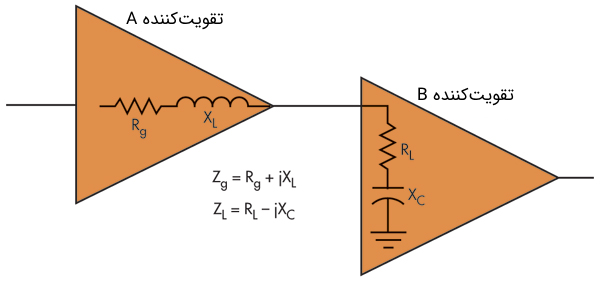
تطبیق امپدانس آنتن خط انتقال

یک مثال دیگر، انتقال حداکثر توان به آنتن است (شکل ۵). در اینجا، امپدانس آنتن با امپدانس خروجی فرستنده مطابقت دارد.

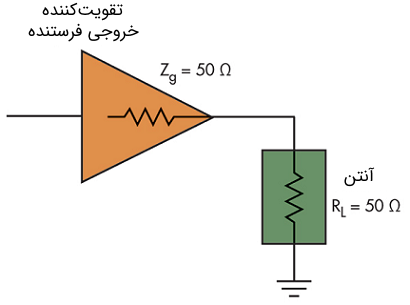
این کاربرد بر ضروری بودن تطبیق امپدانس تأکید می‌کند. خروجی فرستنده معمولاً از طریق خط انتقال به آنتن متصل می‌شود که معمولاً کابل کواکسیال (Coaxial Cable) است. در سایر کاربردها، خط انتقال ممکن است یک «زوج به هم تابیده» (Twisted Pair) یا یک رابط دیگر باشد.

یک کابل هنگامی که طولی بیشتر از $$\lambda / 8$$ در فرکانس کاری داشته باشد تبدیل به خط انتقال می‌شود که در آن، $$\lambda = 300 / f _\text{MHz}$$ است.

برای مثال، طول موج فرکانس $$433\, \text{MHz}$$ برابر است با:

$$\large \lambda = 300/f_\text {MHz} = 300/433 = 0.7 \; \text{m} =27.5 \; \text{in}$$

بنابراین، کابل اتصال اگر طولانی تر از $$0.7/8 = 0.0875$$ متر یا $$3.44$$ اینچ باشد، یک خط انتقال است. همه خطوط انتقال دارای یک امپدانس مشخصه ($$Z_O$$) هستند که تابعی از اندوکتانس و کاپاسیتانس (ظرفیت) خط است:

$$\large Z_O = \sqrt {(L/C)}$$

برای دستیابی به حداکثر انتقال توان از طریق خط انتقال، امپدانس خط نیز باید با امپدانس منبع و بار مطابقت داشته باشد (شکل ۶). اگر امپدانس‌ها با هم مطابقت نداشته باشند، حداکثر توان تحویل نمی‌شود. علاوه بر این، امواج ایستا در امتداد خط گسترش می‌یابند. این بدین معنی است که بار تمام توان ارسال شده از خط را جذب نمی‌کند.

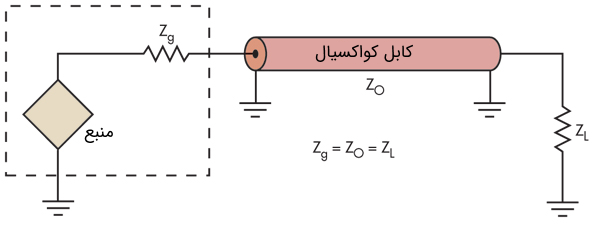
در نتیجه، بخشی از این توان به سمت منبع بازتاب می‌شود و بازدهی کاهش می‌یابد. توان بازتابیده حتی می‌تواند به منبع آسیب برساند. امواج ایستا الگوهای توزیع ولتاژ و جریان در طول خط هستند. ولتاژ و جریان برای یک خط همسان (تطبیق یافته) ثابت هستند، اما اگر امپدانس‌ها مطابقت نداشته باشند، تغییرات زیادی خواهند داشت.

مقدار توان اتلافی در اثر بازتاب تابعی از ضریب بازتاب ($$\Gamma$$) و نسبت موج ایستا (SWR) است. این‌ها با توجه به میزان عدم تطابق بین امپدانس‌های منبع و بار تعیین می‌شوند.

SWR تابعی از امپدانس بار ($$Z_L$$) و خط ($$Z_O$$) است:

$$\large \text{SWR} = Z_L/Z_O , \;\; \;Z_L > Z_O$$

$$\large \text{SWR} = Z_O/Z_L , \;\; \;Z_O > Z_L$$

برای یک تطبق کامل،‌ $$\text{SWR}=1$$ است. فرض کنید $$Z_L = 75\; \Omega$$ و $$Z_O = 50\; \Omega$$ باشند. در نتیجه، $$\text{SWR} = Z_L/Z_O = 75/50 = 1.5$$ خواهد بود.

ضریب بازتاب یکی دیگر از معیارهای تطبیق مناسب است:

$$\large \Gamma = ( Z _ L – Z_ O ) / ( Z _ L + Z _ O )$$

برای یک تطبیق کامل، $$\Gamma$$ برابر با صفر خواهد بود. همچنین می‌توانیم $$\Gamma$$ را از مقدار SWR محاسبه کنیم:

$$\large \Gamma = (\text{SWR} – 1) / ( \text{SWR} + 1)$$

برای مثالی که گفتیم، داریم:

$$\large \Gamma = (\text{SWR} – 1)/(\text{SWR} + 1) = (1.5 – 1)/(1.5 + 1) = 0.5/2.5 = 0.2$$

با نگاهی به میزان توان بازتابی برای مقادیر داده شده SWR (شکل ۷)، می‌توان گفت که SWR برابر با ۲ یا کمتر برای بسیاری از کاربردها کافی است. SWR برابر با ۲ به معنای این است که توان بازتابی ۱۰ درصد است. بنابراین ۹۰ درصد توان به بار می‌رسد.

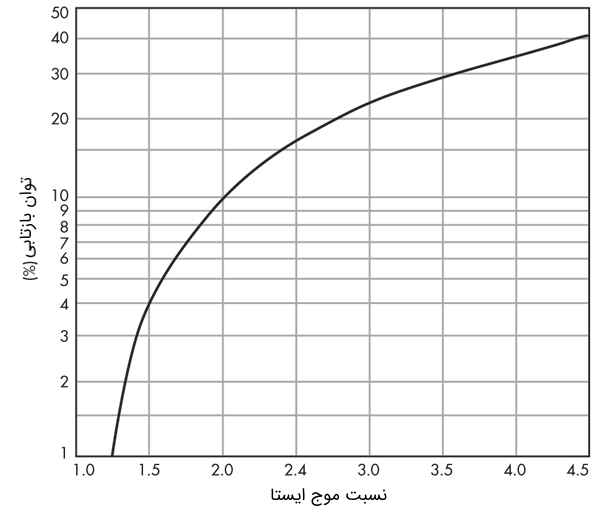
به خاطر داشته باشید که همه خطوط انتقال مانند کابل کواکسیال باعث از بین رفتن دسی بل در هر پا (فوت) می‌شوند. این تلفات باید در هر محاسبه‌ای از توان رسیده به بار در نظر گرفته شود. دیتاشیت‌های کواکسیال این مقادیر را برای فرکانس‌های مختلف ارائه می‌دهند.

نکته مهم دیگر که باید به خاطر بسپاریم این است که اگر امپدانس خط و بار منطبق شوند، طول خط مهم نیست. اما اگر امپدانس خط و بار مطابقت نداشته باشند، ژنراتور یک امپدانس مختلط را مشاهده می‌کند که تابعی از طول خط است.

توان بازتاب شده معمولاً به عنوان تلفات بازگشت ($$P_L$$) بیان و با این عبارت محاسبه می‌شود:

$$\large P_L [\text{dB}] = 10 \log (P_{IN}/P_{REF})$$

$$P_{IN}$$ توان ورودی به خط را نشان می‌دهد و $$P_{REF}$$ توان منعکس شده یا بازتابی است. هر چه مقدار dB بیشتر باشد، توان بازتاب شده کمتر و مقدار توان تحویلی به بار بیشتر می‌شود.

روش های  تطبیق امپدانس

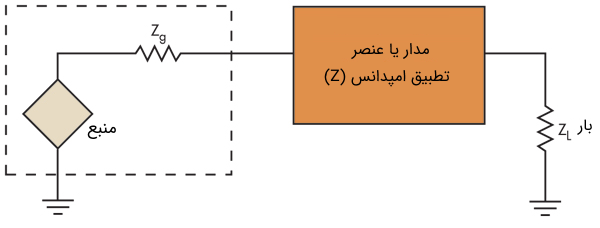
مشکل متداول در عدم تطبیق امپدانس‌های بار و منبع را می‌توان با اتصال یک دستگاه تطبیق امپدانس بین منبع و بار اصلاح کرد (شکل ۸).

دستگاه تطبیق امپدانس ($$Z$$) می‌تواند یک عنصر، مدار یا قطعه‌ای از تجهیزات باشد.

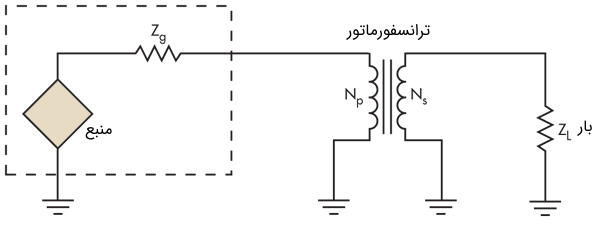
طیف گسترده‌ای از راهکارها برای این تطبیق امپدانس امکان پذیر است. دو مورد از ساده‌ترین آن‌ها، ترانسفورماتور و $$\lambda / 4$$ بخش تطبیق است. ترانسفورماتور با استفاده از نسبت دور (شکل ۹) یک امپدانس را با دیگری مطابقت می‌دهد:

نسبت تبدیل = $$\large N= N_p/N_s$$

که در آن، $$N$$ نسبت تبدیل، $$N_s$$ تعداد دور سیم پیچ ثانویه و $$N_p$$ تعداد دور سیم پیچ اولیه ترانسفورماتور است.

رابطه نسبت تبدیل با امپدانس‌ها به صورت زیر است:

$$\large Z_p/Z_s = (N_p/N_s)^2$$  یا  $$\large N_p/N_s = \sqrt{(Z_p/Z_s)}$$

$$Z_p$$ نمایانگر امپدانس اولیه یا امپدانس خروجی منبع ($$Z_g$$) است. همچنین، $$Z_s$$ نشان دهنده امپدانس ثانویه یا بار ($$Z_L$$) است.

به عنوان مثال، امپدانس خروجی یک منبع $$300\;\Omega$$ توسط یک ترانسفورماتور با نسبت تبدیل $$2:1$$ با امپدانس بار $$75\: \Omega$$ تطبیق داده می‌شود:

$$\large N_p/N_s = \sqrt {(Z_p/Z_s)} = \sqrt {(300/75)} = \sqrt 4 = 2$$

ترانسفورماتورِ بسیار کارا، از پهنای باند گسترده‌ای برخوردار است. با وجود هسته‌های فریت مدرن، این روش تا حدود چندصد مگاهرتز مفید است.

از یک اتوترانسفورماتور با تنها یک سیم‌پیچ و تپ (لغزانه) نیز می‌توان برای تطبیق امپدانس استفاده کرد. بسته به اتصالات، امپدانس‌ها را می‌توان کم (شکل ۱۰.الف) یا زیاد (شکل ۱۰.ب) کرد.

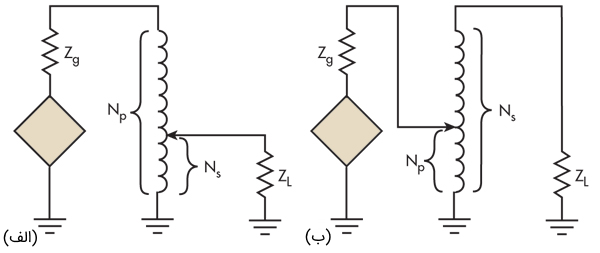
فرمول‌های مورد استفاده برای ترانسفورماتورهای استاندارد برای اتوترانسفورماتورها نیز کاربرد دارند. سیم‌پیچ ترانسفورماتور یک سلف است و حتی ممکن است بخشی از یک مدار رزونانس با یک خازن باشد.

راهکار تطبیق مقاومت در خط انتقال از $$\lambda/4$$ خط انتقال (که یک ربع-بخش (Q-Section) نامیده می‌شود) از یک امپدانس مشخصه برای تطبیق با بار با منبع استفاده می‌کند (شکل ۱۱).

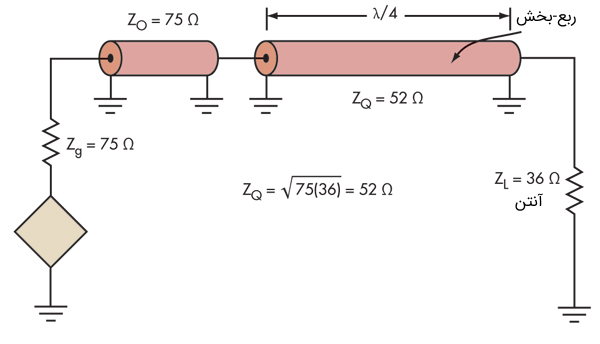
در شکل بالا، $$Z_Q$$ امپدانس مشخصه خط ربع-بخش است. همچنین، $$Z_O$$ امپدانس مشخصه خط انتقال ورودی از منبع و $$Z_L$$ امپدانس بار است.

در اینجا، امپدانس $$36\; \Omega$$ یک آنتن صفحه عمودی $$\lambda / 4$$ با امپدانس خروجی $$75 \; \Omega$$ فرستنده از طریق یک کابل کواکسیال $$52 \; \Omega$$ مطابقت دارد:

$$\large Z_Q = \sqrt {(75)(36)} = \sqrt {2700} = 52\; \Omega$$

با فرض فرکانس کاری $$50\; \text{MHz}$$، طول موج برابر است با:

$$\large \lambda = 300 / f _ \text{MHz} = 300/50 = 6 \; \text{m} \approx 20 \;\text{ft}$$

$$\large \lambda /4 = 20/4 = 5 \;\text {ft}$$

با فرض استفاده از خط انتقال کواکسیال $$52\;Ω \;\;\text {RG-8/U}$$ با ضریب سرعت $$0.66$$، داریم:

$$\large \lambda /4 = 5 \; \text{ft}\;\times (0.66) = 3.3 \;\text {ft}$$

هنگام استفاده از این روش باید چند محدودیت مهم را در نظر بگیریم. ابتدا باید یک کابل با امپدانس مشخصه مورد نظر در دسترس باشد. این مورد همیشه اتفاق نمی‌افتد، زیرا اکثر کابل‌ها فقط در امپدانس‌های پایه (۵۰، ۷۵، ۹۳ و ۱۲۵ اهم) موجود هستند. دوم اینکه طول کابل در فرکانس کاری برای محاسبه طول موج و ضریب سرعت باید لحاظ شود.

به طور خاص، این محدودیت‌ها هنگام کار در فرکانس‌های پایین، روی این تکنیک تأثیر می‌گذارند. با این حال، هنگام استفاده از میکرواستریپ یا ریزنوار (Microstrip) یا خط نواری (Stripline) بر روی برد مدار چاپی (PCB)، این روش را می‌توان به راحتی در فرکانس UHF و مایکروویو اعمال شود. در این حالت، تقریباً هر امپدانس مشخصه مورد نظر را می‌توان استفاده کرد.

مثالی از شبکه های تطبیق امپدانس

شبکه‌های تطبیق امپدانس مختلفی از قبیل شبکه‌های L، شبکه‌های $$\pi$$، شبکه‌های T و... وجود دارند که در این بخش، برای آشنایی شبکه L را معرفی می‌کنیم.

کاربردهای اصلی شبکه‌های L تطبیق امپدانس در مدارهای RF، فرستنده‌ها و گیرنده‌ها است. شبکه‌های L در تطبیق خروجی تقویت‌کننده با ورودی طبقه بعدی مفید هستند. کاربرد دیگر این شبکه‌ها تطبیق امپدانس آنتن با خروجی فرستنده یا ورودی گیرنده است. هر مدار RF که محدوده فرکانس باریک را پوشش می‌دهد، نامزد استفاده از شبکه L است.

چهار نسخه اساسی از شبکه L وجود دارد که دو نسخه ‌پایین‌گذر و دو نسخه بالاگذر هستند (شکل ۱۲). نسخه‌های پایین‌گذر از آنجا که هارمونیک‌ها، نویز و سایر سیگنال‌های ناخواسته را تضعیف می‌کنند، بسیار مورد استفاده قرار می‌گیرند و معمولاً در طراحی‌های RF ضروری هستند. معیارهای اصلی طراحی اندازه و ابعاد نسبی امپدانس خروجی ژنراتور و امپدانس بار است.

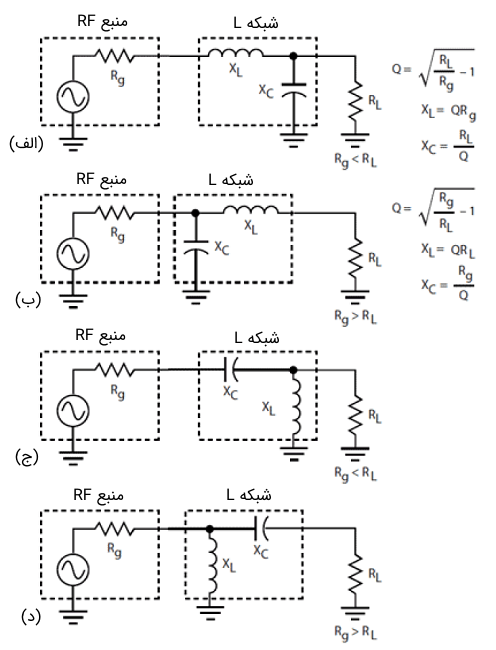
امپدانس هایی که تطبیق داده می‌شوند، $$Q$$ مدار را تعیین می‌کنند که نمی‌توان آن را مشخص یا کنترل کرد. اگر کنترل $$Q$$ و پهنای باند ضروری باشد، شبکه T یا $$\pi$$ انتخاب‌های بهتری هستند.

علی‌رغم آنکه شبکه L بسیار متنوع است، اما ممکن است پاسخگوی هر نیازی نباشد. محدودیت‌هایی برای محدوه امپدانس‌هایی که باید تطبیق یابند وجود دارد. در برخی موارد، مقادیر محاسبه شده اندوکتانس یا کاپاسیتانس ممکن است خیلی بزرگ یا کوچک باشند تا برای یک محدوده فرکانس مشخص عملی شوند. گاهی اوقات با جابه‌جایی از یک نسخه پایین‌گذر به یک نسخه بالاگذر یا برعکس، این مشکل برطرف می‌شود.

برای مثال، می‌خواهیم امپدانس خروجی یک آمپلی‌فایر ترانزیستوری RF توان پایین را با بار خروجی $$50\; \Omega$$ تطبیق دهیم ($$50\; \Omega$$ یک استاندارد جهانی برای اغلب گیرنده‌ها، فرستنده‌ها و مدارهای RF است). اکثر تقویت‌کننده‌های توان امپدانس خروجی کمی (معمولاً کمتر از $$50\; \Omega$$) دارند.

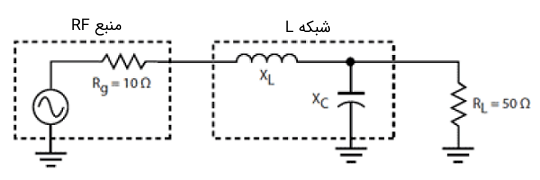
شکل ۱۳ مدار مورد نظر را نشان می‌دهد. امپدانس خروجی تقویت‌کننده (ژنراتور) را ۱۰ اهم با فرکانس ۷۶ مگاهرتز فرض کنید. می‌خواهیم مقادیر سلف و خازن مورد نیاز را با استفاده از فرمول‌های داده شده در شکل ۱۲ محاسبه کنیم.

$$\large Q = \sqrt { (R _ L / R _ g ) – 1 } = \sqrt { ( 5 0 / 1 0 ) – 1 } = \sqrt { (5) – 1} = 2$$

$$\large X _ L = Q R _ g = 2 (1 0 ) = 2 0 \; \Omega$$

$$\large L = X _ L / 2 \pi f = 2 0 / [ 2 ( 3 . 1 4 ) ( 7 6 \times 1 0 6 ) ]= 4 2\; \text {nH}$$

$$\large X _ C = R _ L / Q = 5 0 / 2 = 2 5 \; \Omega$$

$$\large C = 1 / 2 \pi f X _C = 1 / [ 2 ( 3 . 1 4 ) ( 7 6 \times 1 0 6 ) ( 2 5 ) ] = 8 3 . 8 \; \text {pF}$$

در این راه ‌حل، از هرگونه راکتانس امپدانس خروجی مانند کاپاسیتانس یا اندوکتانس خروجی تقویت‌کننده ترانزیستوری و هرگونه راکتانس بار را که می‌تواند با کاپاسیتانس موازی یا با اندوکتانس سری شود، چشم‌پوشی شده است. وقتی این عوامل شناخته شده و معلوم باشند، مقادیر محاسبه شده را می‌توان تصحیح کرد.

پهنای باند (BW) مدار با توجه به مقدار Q کم ۳ نسبتاً گسترده است:

$$\large \text {BW} = f/Q = (76 \times10^6)/2 = 38 \times 10^6 = 38\; \text{MHz}$$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش مهندسی برق
• آموزش مدارهای الکتریکی 1
• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش مدارهای مخابراتی
• مدار سه فاز — از صفر تا صد
• منبع تغذیه سوئیچینگ — به زبان ساده
• ال ای دی (LED) چیست؟ — به زبان ساده

^^