تبدیل هاف (Hough Transform) در پردازش تصویر — از صفر تا صد
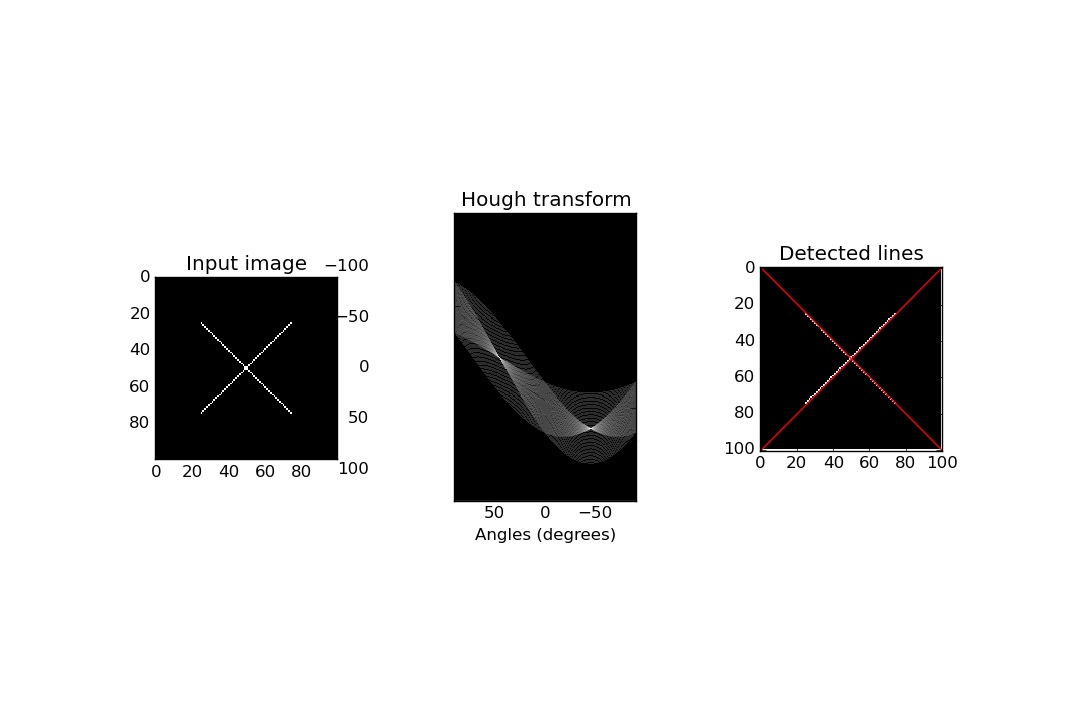
«تبدیل هاف» (Hough Transform) تکنیکی است که به وسیله آن میتوان خطوط راست و حتی اشکال دایرهای را در یک تصویر تشخیص داد. در این مطلب قصد داریم به بیان نحوه تشخیص خطوط و دایرهها در یک تصویر با استفاده از تبدیل هاف بپردازیم و آن را با استفاده از کتابخانه OpenCV در زبانهای پایتون و نیز ++C و نیز متلب پیادهسازی کنیم.
تبدیل هاف چیست؟
در واقع میتوان تبدیل هاف را یک شیوه «استخراج ویژگی» (Feature Extraction) دانست که به وسیله آن شکلهای ساده مانند خط و دایره در یک تصویر تشخیص داده میشوند. توجه کنید که منظور از یک شکل ساده، شکلی است که بتوان آن را تنها با استفاده از تعداد کمی پارامتر نشان داد.
به عنوان مثال، یک خط را میتوان فقط به کمک دو پارامتر شیب و عرض از مبدا نشان داد. همچنین دایره با کمک ۳ پارامتر قابل نشان دادن است که عبارتند از مختصات X و Y و نیز شعاع R دایره. تبدیل هاف در یافتن این شکلها در یک تصویر به صورت فوقالعاده عمل میکند. یکی از مهمترین مزایای تبدیل هاف در یافتن خط و دایره در تصویر این است که نسبت به همپوشانی حساس نیست. حال در ادامه قصد داریم به بررسی نحوه کار تبدیل هاف از طریق یک مثال بپردازیم.
تشخیص خط در تصویر با استفاده از تبدیل هاف
در تصویر زیر نمایی از یک خط راست در مختصات قطبی نشان داده شده است.
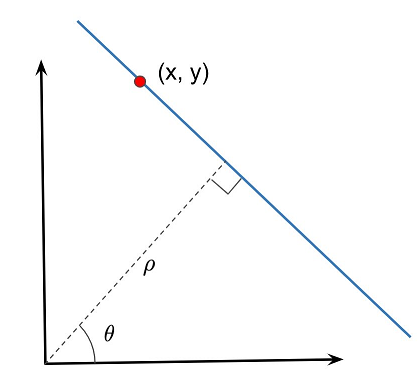
معادله یک خط در مختصات قطبی به صورت زیر نوشته میشود:
$$ \rho = x \cos ( \theta ) + y \sin ( \theta ) $$
در این رابطه، $$ \rho $$ برابر با فاصله عمودی خط از مبدا بر حسب پیکسل و $$ \theta $$ زاویه خط با مبدا است که بر حسب رادیان اندازه گرفته میشود. این موارد در تصویر فوق نیز به خوبی نشان داده شده است. ممکن است این سوال پیش بیاید که چرا از معادله خط در مختصات دکارتی که به صورت زیر است، استفاده نمیکنیم:
$$ y = m x + c $$
دلیل عدم استفاده از مختصات دکارتی این است که مقدار شیب خط یا m، میتواند مقادیر بین $$ - \infty $$ تا $$ \infty $$ را به خود اختصاص دهد، در حالی که در تبدیل هاف مقادیر پارامترها باید محدود باشند. همچنین سوال دیگری که ممکن است در مورد تبدیل هاف پیش بیاید این است که در معادله مربوط به خط در مختصات قطبی، مقدار $$ \theta $$ محدود است، اما آیا پارامتر $$ \rho $$ در بازه مقادیر بین 0 تا $$ \infty $$ نیست؟ در پاسخ باید گفت این مقادیر تنها از لحاظ تئوری درست هستند، اما در عمل پارامتر $$ \rho $$ نیز محدود است؛ زیرا خود تصویر محدود است.
انباشتگر (Accumulator)
زمانی که میگوییم یک خط در فضای دو بعدی با دو پارامتر $$ \rho $$ و $$ \theta $$ مشخص میشود، به این معنی است که اگر دو مقدار تصادفی برای پارامترهای $$ \rho $$ و $$ \theta $$ انتخاب کنیم، در این صورت یک خط در فضای دو بعدی به دست میآید. یک آرایه دو بعدی را در نظر بگیرید که محور x دارای تمام مقادیر ممکن برای $$ \theta $$ و محور y دارای تمام مقادیر ممکن برای $$ \rho $$ باشد. هر عضو این آرایه دو بعدی متناظر با یک خط در فضا است. به این آرایه دو بعدی انباشتگر میگویند. در تصویر زیر نمایی از این مفهوم نشان داده شده است.
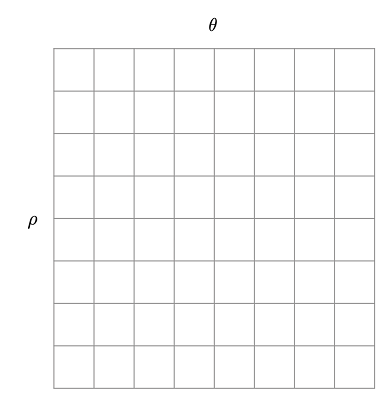
از مقادیر موجود در آرایه دو بعدی انباشتگر برای جمعآوری اطلاعات درباره این امر استفاده میکنیم که کدام خطوط در تصویر وجود دارند. سلول بالا سمت چپ، متناظر با $$ (- R , 0 ) $$ و سلول پایین سمت راست متناظر با $$ ( R , \pi ) $$ است. هر چقدر مدارک بیشتری درباره حضور یک خط با پارامتر $$ \rho $$ و $$ \theta $$ جمعآوری شود، خواهیم دید که مقادیر درون سلولهای این آرایه دو بعدی کم کم $$ ( \rho , \theta ) $$ افزایش خواهند یافت. برای تشخیص یک خط در تصویر باید گامهای زیر را انجام دهیم.
گام اول: مقداردهی اولیه (Initialize) آرایه دو بعدی
ابتدا لازم است که یک آرایه انباشتگر بسازیم. تعداد سلولهایی که در شبکه حضور دارند، یک پارامتر طراحی است که باید آن را مشخص کرد. حال فرض کنید یک شبکه انباشتگر ۱۰ در ۱۰ در انتخاب کردهایم. این امر بدین معنی است که $$ \rho $$ فقط ۱۰ مقدار متمایز میتواند بگیرد، همچنین $$ \theta $$ نیز فقط ۱۰ مقدار متفاوت را میتواند به خود اختصاص دهد. بنابراین در حالت کلی ما قادر به تشخیص ۱۰۰ خط متفاوت هستیم. البته اندازه انباشتگر که انتخاب میکنیم به رزولوشن تصویر نیز بستگی دارد. اما در اینجا و به عنوان شروع یادگیری لازم نیست زیاد راجع به تنظیم صحیح این پارامتر نگران باشید. ابتدا یک مقدار مانند ۲۰ در ۲۰ را انتخاب کنید و نتیجه را با این فرض مشاهده کنید.
گام دوم: تشخیص لبه (Edge Detection)
حال که ابعاد شبکه را انتخاب کردیم و انباشتگر نیز تنظیم شد، میخواهیم برای هر سلول در انباشتگر مدارک کافی جمعآوری کنیم؛ زیرا هر سلول در این شبکه متناظر با یک خط است. اما ایدهای که در پس جمعآوری مدارک وجود دارد این است که اگر یک خط مرئی در تصویر وجود داشته باشد، الگوریتم تشخیص لبه در مرزهای خط فعال (Fire) میشود و این مرزها را نشان دهد. پیکسلهای لبه تصویر میتواند مدرک کافی برای حضور یک خط در تصویر را فراهم کنند. خروجی الگوریتم تشخیص لبه یک آرایه از پیکسلهای لبه تصاویر به صورت زیر است:
$$ [ ( x _ 1 , y _ 1 ), ( x _ 2 , y _ 2 ) . . . (x _ n , y _ n ) ] $$
گام سوم: انتخاب پیکسلهای لبه
برای هر پیکسل لبه $$ ( x , y ) $$ در آرایه فوق، مقدار $$ \theta $$ را در بازه ۰ تا $$ \pi $$ تغییر میدهیم و آن را در معادله خط در مختصات قطبی جایگزین میکنیم تا یک مقدار برای $$ \rho $$ به دست آید. در تصویر زیر مقادیر $$ \theta $$ را در این بازه برای سه پیکسل تغییر دادهایم و مقادیر $$ \rho $$ را با استفاده از معادله خط به دست آوردهایم. این سه پیکسل توسط سه منحنی رنگی نشان داده شدهاند.
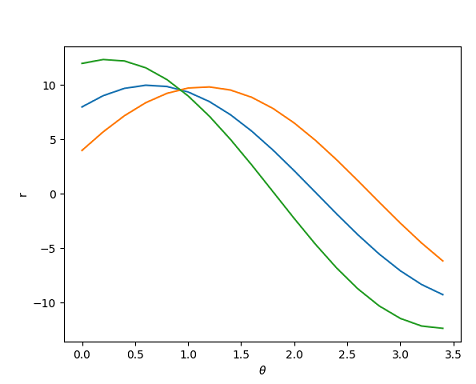
همان طور که در تصویر بالا دیده میشود، منحنیها در یک نقطه با همه برخورد میکنند که نشان دهنده این است که یک خط با پارامترهای $$ \theta = 1 $$ و $$ \rho = 0 . 9 5 $$ از آن نقطه عبور میکند. معمولا در یک تصویر صدها پیکسل مربوط به لبه داریم و از انباشتگر برای یافتن تقاطع تمام منحنیهای ایجاد شده توسط پیکسلهای لبه استفاده میکنیم. در ادامه به بررسی نحوه انجام این کار میپردازیم.
فرض کنید که انباشتگر سایز ۲۰ در ۲۰ داشته باشد. بنابراین ۲۰ مقدار متمایز برای $$ \theta $$ وجود دارد و در نتیجه برای هر پیکسل لبه $$ ( x , y ) $$ نیز ۲۰ جفت $$ ( \rho , \theta ) $$ را با استفاده از معادله قطبی خط خواهیم داشت. مقادیر سلولهای انباشتگر متناظر با این ۲۰ مقدار $$ ( \rho , \theta ) $$ به تدریج افزایش مییابند. برای هر پیکسل لبه این محاسبات را انجام میدهیم و در نتیجه یک انباشتگر خواهیم داشت که دارای اطلاعات کافی درباره تمام خطوط موجود در تصویر است.
میتوانیم به سادگی تمام سلولهای انباشتگر که بالاتر از یک حد آستانه هستند را انتخاب کنیم تا خطوط تصویر را پیدا کنیم. هر چقدر میزان آستانه بالاتر باشد، تعداد خطوط قوی کمتری را پیدا خواهیم کرد و هر چه آستانه را مقداری پایینتر قرار دهیم، در این صورت تعداد خطوط بیشتری را به دست میآوریم که حتی شامل خطوط ضعیف نیز هستند.
تشخیص خطوط با تبدیل هاف در OpenCV
در کتابخانه OpenCV تشخیص خط با استفاده از تبدیل هاف را میتوان با دو تابع HoughLines یا HoughLinesP پیادهسازی کرد. HoughLinesP مربوط به نوع دیگری از تبدیل هاف است که «تبدیل هاف احتمالاتی» (Probabilistic Hough Transform) نام دارد. این تابع آرگومانهای زیر را به عنوان ورودی دریافت میکند.
- edges: خروجی آشکارساز لبه.
- lines: یک بردار برای ذخیرهسازی مختصات شروع و پایان خطوط.
- theta: پارامتر رزولوشن $$ \rho $$ در پیکسلها.
- threshold: تعداد کمینه نقاط تقاطع برا تشخیص یک خط.
کدهای مربوط به پیادهسازی تبدیل هاف در زبان پایتون در ادامه قرار داده شدهاند:
1# Read image
2img = cv2.imread('lanes.jpg', cv2.IMREAD_COLOR) # road.png is the filename
3# Convert the image to gray-scale
4gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
5# Find the edges in the image using canny detector
6edges = cv2.Canny(gray, 50, 200)
7# Detect points that form a line
8lines = cv2.HoughLinesP(edges, 1, np.pi/180, max_slider, minLineLength=10, maxLineGap=250)
9# Draw lines on the image
10for line in lines:
11 x1, y1, x2, y2 = line[0]
12 cv2.line(img, (x1, y1), (x2, y2), (255, 0, 0), 3)
13# Show result
14cv2.imshow("Result Image", img)همچنین برای پیادهسازی تبدیل هاف روی یک تصویر به زبان ++C باید به طریق زیر عمل کنیم:
1// Read the image as gray-scale
2Mat img = imread('lanes.jpg', IMREAD_COLOR);
3// Convert to gray-scale
4Mat gray = cvtColor(img, COLOR_BGR2GRAY);
5// Store the edges
6Mat edges;
7// Find the edges in the image using canny detector
8Canny(gray, edges, 50, 200);
9// Create a vector to store lines of the image
10vector<Vec4i> lines;
11// Apply Hough Transform
12HoughLinesP(edges, lines, 1, CV_PI/180, thresh, 10, 250);
13// Draw lines on the image
14for (size_t i=0; i<lines.size(); i++) {
15 Vec4i l = lines[i];
16 line(src, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(255, 0, 0), 3, LINE_AA);
17}
18// Show result image
19imshow("Result Image", img);نتایج تشخیص خط با تبدیل هاف
در ادامه تصاویری از نتیجه اعمال تبدیل هاف برای تشخیص خطوط در تصویر نشان داده شدهاند.

البته باید این نکته را در ذهن داشته باشیم که کیفیت تشخیص خط با کمک تبدیل هاف عمیقا به کیفیت عملکرد الگوریتم تشخیص لبه بستگی دارد و به همین دلیل در کاربردهای واقعی، زمانی از تبدیل هاف برای تشخیص خطوط استفاده میشود که بتوان محیط را کنترل کرد و در نتیجه بتوان یک نگاشت لبه مقاوم را به دست آورد. همچنین راه حل دیگر برای استفاده از این تبدیل این است که یک الگوریتم تشخیص لبه را برای انواع خاصی از لبهها آموزش بدهیم که بیشتر در جستوجوی آن نوع از لبهها هستیم.
تشخیص دایره در تصویر با استفاده از تبدیل هاف
در مورد تشخیص خط با تبدیل هاف، به دو پارامتر $$ ( \rho , \theta ) $$ نیاز داریم، اما برای تشخیص یک دایره به سه پارامتر نیاز داریم که به صورت زیر هستند:
- $$ ( X , Y ) $$: مختصات موقعیت مرکز دایره
- r: شعاع دایره
در نتیجه برای تشخیص دایره با تبدیل هاف به سه انباشتگر نیاز داریم که هر بعد انباشتگر متعلق به یکی از پارامترها است. معادله یک دایره را میتوان به صورت زیر بیان کرد:
$$ ( x - x _0 ) ^ 2 + ( y - y _ 0 ) ^ 2 = r ^ 2 $$
برای تشخیص دایره در یک تصویر گامهای زیر لازم هستند:
- در تصویر مورد نظر، لبه را با استفاده از تشخیصگرهای لبه مانند Canny شناسایی کنید.
- برای تشخیص دایره در یک تصویر، باید یک حد آستانه را برای مقادیر کمینه و بیشینه شعاع در نظر بگیرید.
- مدارک برای حضور دایرههای با مرکز و شعاع مختلف، در یک آرایه انباشتگر سه بعدی جمعآوری میشوند.
در OpenCV از تابع HoughCircles برای تشخیص دایره در تصویر استفاده میشود. این تابع پارامترهای زیر را به عنوان ورودی دریافت میکند:
- image: تصویر ورودی
- method: روش تشخیص
- mindst: کمینه فاصله بین مراکز دایرههای تشخیص داده شده.
- param_1 و param_2: متدهای مخصوص مربوط به روش.
- min_Radius: کمینه شعاع دایرههایی که باید تشخیص داده شوند.
- max_Radius: بیشینه شعاع دایرههایی که باید تشخیص داده شوند.
حال کدهای مربوط به یافتن دایره در یک تصویر با کمک تبدیل هاف را با زبان پایتون به صورت زیر مینویسیم:
1# Read image as gray-scale
2img = cv2.imread('circles.png', cv2.IMREAD_COLOR)
3# Convert to gray-scale
4gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
5# Blur the image to reduce noise
6img_blur = cv2.medianBlur(gray, 5)
7# Apply hough transform on the image
8circles = cv2.HoughCircles(img_blur, cv2.HOUGH_GRADIENT, 1, img.shape[0]/64, param1=200, param2=10, minRadius=5, maxRadius=30)
9# Draw detected circles
10if circles is not None:
11 circles = np.uint16(np.around(circles))
12 for i in circles[0, :]:
13 # Draw outer circle
14 cv2.circle(img, (i[0], i[1]), i[2], (0, 255, 0), 2)
15 # Draw inner circle
16 cv2.circle(img, (i[0], i[1]), 2, (0, 0, 255), 3)همچنین کد یافتن دایره در یک تصویر با کمک تبدیل هاف به زبان ++C به صورت زیر است:
1// Read the image as gray-scale
2img = imread("circles.png", IMREAD_COLOR);
3// Convert to gray-scale
4gray = cvtColor(img, COLOR_BGR2GRAY);
5// Blur the image to reduce noise
6Mat img_blur;
7medianBlur(gray, img_blur, 5);
8// Create a vector for detected circles
9vector<Vec3f> circles;
10// Apply Hough Transform
11HoughCircles(img_blur, circles, HOUGH_GRADIENT, 1, img.rows/64, 200, 10, 5, 30);
12// Draw detected circles
13for(size_t i=0; i<circles.size(); i++) {
14 Point center(cvRound(circles[i][0]), cvRound(circles[i][1]));
15 int radius = cvRound(circles[i][2]);
16 circle(img, center, radius, Scalar(255, 255, 255), 2, 8, 0);
17}توجه به این نکته ضروری است که تابع HoughCircles الگوریتم تشخیص لبه Canny را به صورت توکار در خود دارد. بنابراین لازم نیست لبهها را به صورت جداگانه تشخیص دهیم.
نتایج تشخیص دایره با تبدیل هاف
در تصاویر زیر نتیجه تشخیص دایره با کمک تبدیل هاف نشان داده شده است.
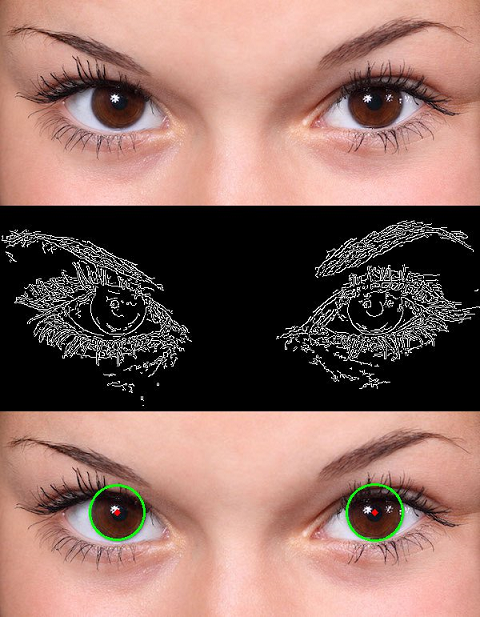
در مورد تبدیل هاف برای یافتن دایره در تصاویر نیز نکتهای که وجود دارد این است که کیفیت نهایی خروجی و تشخیص، تا حد زیادی به کیفیت تشخیص لبه بستگی دارد. همچنین عامل مهم دیگر در کیفیت خروجی این است که چه مقدار دانش پیشین درباره اندازه دایرهای در اختیار است که قصد تشخیص آن در تصویر را داریم.

تبدیل هاف در متلب
در ادامه قصد داریم به بررسی کدهای تبدیل هاف در متلب نیز بپردازیم. برای این کار ابتدا باید تصویر مورد نظر را با دستور زیر بارگذاری کنیم.
توجه کنید که تصویر چرخش داده شده است.
1I = imread('circuit.tif');
2rotI = imrotate(I,33,'crop');
3imshow(rotI)سپس با استفاده از دستور زیر میتوانیم لبهها را در تصویر پیدا کنیم.
1BW = edge(rotI,'canny');
2imshow(BW);نتیجه به صورت زیر خواهد بود.
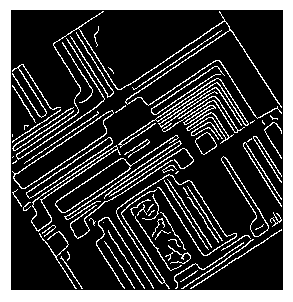
حال میتوانیم با دستورات زیر ابتدا تبدیل هاف را روی تصویر انجام دهیم و سپس مقادیر به دست آمده در خروجی تابع را ترسیم کنیم.
1[H,theta,rho] = hough(BW);1figure
2imshow(imadjust(rescale(H)),[],...
3 'XData',theta,...
4 'YData',rho,...
5 'InitialMagnification','fit');
6xlabel('\theta (degrees)')
7ylabel('\rho')
8axis on
9axis normal
10hold on
11colormap(gca,hot)تبدیل هاف به صورت زیر خواهد بود.
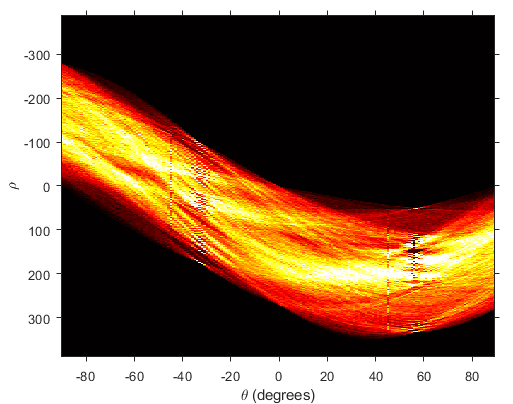
حال مقادیر پیک را در ماتریس H تبدیل هاف مشخص میکنیم و با دستورات زیر آن ها را رسم میکنیم.
1P = houghpeaks(H,5,'threshold',ceil(0.3*max(H(:))));
2x = theta(P(:,2));
3y = rho(P(:,1));
4plot(x,y,'s','color','black');نتیجه در تصویر زیر نمایش داده شده است.
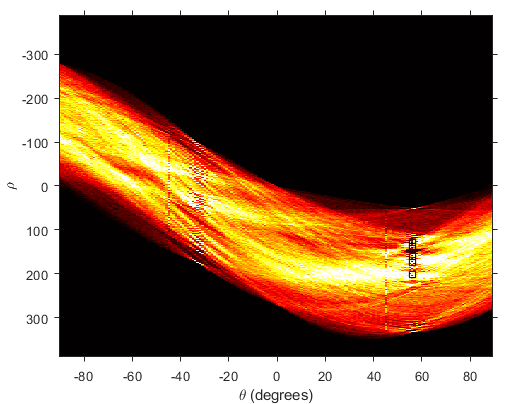
در نهایت با استفاده از تابع houghlines میتوانیم خطوط به دست آمده با استفاده از تبدیل هاف را ترسیم کنیم.
1lines = houghlines(BW,theta,rho,P,'FillGap',5,'MinLength',7);
2figure, imshow(rotI), hold on
3max_len = 0;
4for k = 1:length(lines)
5 xy = [lines(k).point1; lines(k).point2];
6 plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');
7
8 % Plot beginnings and ends of lines
9 plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
10 plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
11
12 % Determine the endpoints of the longest line segment
13 len = norm(lines(k).point1 - lines(k).point2);
14 if ( len > max_len)
15 max_len = len;
16 xy_long = xy;
17 end
18end
19% highlight the longest line segment
20plot(xy_long(:,1),xy_long(:,2),'LineWidth',2,'Color','red');خطوط تصویر به درستی و با دقت بالایی مشخص میشوند.

اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای پردازش تصویر و ویدئو
- آموزش مقدماتی پردازش تصویر با OpenCV در Python (پایتون)
- مجموعه آموزشهای برنامهنویسی پایتون Python
- آموزش برنامه نویسی Python (پایتون) – مقدماتی
- پردازش تصویر در متلب — راهنمای جامع
- پردازش تصویر با پایتون — راهنمای کاربردی
- بینایی کامپیوتر چیست؟ — به زبان ساده
^^











دستور اصلی تبدیل هاف توی متلب رو داخل کد ننوشتین
فقط اشاره ای به این نشده که این الگوریتم به چه میزان و به چه طریقی عملیات چرخش رو روی تصویر اعمال میکند.
ممنون
سلام. کد بازبینی و اصلاح شد.
از همراهی و بازخوردتان سپاسگزاریم.
سلام
ممنون از توضیحاتتون
یک سوال در کد متلب
imadjust(rescale(H)) منظورتون از H چیست؟
سلام.
منظور از H تبدیل هاف استاندارد است.
از همراهی شما با مجله فرادرس خوشحالیم.