تبدیل عدد اعشاری به کسر – به زبان ساده + حل تمرین و مثال

در آموزش‌های پیشین مجله فرادرس، اعداد اعشاری و اعداد کسری آشنا شدیم. همچنین روش تبدیل کسر به اعشار را بیان کردیم. در این آموزش، می‌خواهیم ببینیم روش تبدیل عدد اعشاری به کسر چگونه است. همچنین، مثال‌های متنوعی را حل خواهیم کرد.

قبل از پرداختن به تبدیل عدد اعشاری اعداد اعشاری و کسری را مرور می‌کنیم.

مروری بر اعداد اعشاری و اعداد کسری

اَعشار جمع واژه عربی عُشر (به‌معنی یک‌دهم) است. به همین دلیل است که اعشار معادل با یک‌دهم‌ها و یکصدم‌ها و... است. آنچه ما در اعداد اعشاری با آن سر و کار داریم، همین یک‌دهم‌ها و یک‌صدم‌ها و... هستند که اعداد اعشاری را می‌سازند. برای مثال، اعداد $$1.5$$، $$2.8$$، $$0.9$$، $$-0.01$$ و... اعدادی اعشاری هستند.

کسرها نیز اعدادی هستند که با تقسیم تعریف می‌شوند و برای نشان دادن هر تعداد از قسمت‌های مساوی یک چیز به‌کار می‌روند. در واقع، کسرها اعدادی حقیقی به‌فرم $$\frac m n$$ هستند که در آن‌ها $$m$$ و $$n$$ اعدادی صحیح‌ هستند. عدد $$m$$ صورت کسر و عدد $$n$$ مخرج کسر نامیده می‌شود. بنابراین، در کسر $$\frac 45$$ عدد $$4$$ صورت و عدد $$5$$ مخرج کسر است و آن را «چهار پنجم» می‌خوانیم.

در ادامه، با روش تبدیل اعداد اعشاری به کسر آشنا می‌شویم.

تبدیل اعداد اعشاری به کسر

در این بخش، با تبدیل اعداد اعشاری به کسر آشنا می‌شویم. این کار را برای دو حالت اعداد کوچک‌تر از یک و بزرگ‌تر از یک بیان می‌کنیم.

فیلم آموزش ریاضی – پایه هشتم + گواهینامه در فرادرس

کلیک کنید

تبدیل اعداد اعشاری کوچک‌تر از یک به کسر

برای تبدیل اعداد اعشاری به اعداد کسری یک راه بسیار ساده این است که همان چیزی را که می‌خوانیم، بنویسیم. برای مثال، عدد ۰٫۳۵ را در نظر بگیرید. این عدد را به‌صورت «سی‌وپنج صدم» می‌خوانیم که معنی آن سی‌وپنج تا از صد تا است. سی‌وپنج تا از صد تا به شکل کسری $$\frac {35} { 100}$$ نوشته می‌شود. به همین ترتیب، چند مثال زیر را نیز داریم:

• ۰٫۱ برابر است با یک دهم یا یکی روی ده یا یکی از ده تا یا $$\frac {1} { 10}$$
• ۰٫۰۱ برابر است با یک صدم یا یکی از صد تا یا یک روی صد یا $$\frac {1} { 100}$$
• ۰٫۰۰۱ برابر است یک هزارم یا یک روی هزار یا یکی از هزار تا یا $$\frac { 1 } { 1000}$$
• ۰٫۵۴ برابر است با پنجاه‌وچهار صدم یا پنجاه‌وچهار از صد یا پنجاه‌وچهار بر صد یا $$\frac {54}{100}$$
• ۰٫۰۳۲ برابر است با سی‌ودو از صد یا سی‌ودو صدم یا سی‌ودو بر صد یا $$\frac{32}{1000}$$

تا اینجا، آموختیم که چگونه می‌توان اعداد اعشاری را به کسر تبدیل کرد. برای مثال، دیدیم که $$0.54$$ را می‌توان به‌صورت $$\frac {54}{100}$$ نوشت. اما اگر دقت کنیم، می‌توانیم این کسر را ساده‌تر کنیم. هم صورت و هم مخرج بر $$2$$ بخش‌پذیر هستند. بنابراین، می‌توان نوشت:

$$\frac {54}{100} = \frac {27\times 2}{50\times 2} = \frac {27}{50}$$

در ادامه تبدیل عدد اعشاری به کسر، می‌توانیم کسر را تا جای ممکن ساده کنیم. برای مثال، به‌جای $$\frac 5 {10}$$ می‌توانیم $$\frac 12$$ را بنویسیم.

نکته: یک راه دیگر برای نوشتن اعداد اعشاری به‌صورت یک کسر این است که به تعداد ابتدا کسر را تشکیل دهیم، سپس اعداد سمت راست اعشار را در صورت قرار دهیم. همچنین، در مخرج کسر عدد ۱ را قرار داده و سپس به‌اندازه تعداد ارقام سمت راست جلوی عدد ۱ صفر قرار می‌دهیم.

برای مثال، فرض کنید می‌خواهیم عدد اعشاری $$0.075$$ را به کسر تبدیل کنیم. طبق آنچه گفتیم، باید عدد سمت راست اعشار را که $$075$$ یا همان $$75$$ است، در صورت کسر بنویسیم. تعداد ارقام سمت راست اعشار ۳ است و در مخرج عدد $$1000$$ را قرار می‌دهیم. بنابراین، عدد $$0.075$$ به‌شکل زیر نوشته می‌شود:

$$0.075 = \frac { 75 } { 1000 }$$

تبدیل اعداد اعشاری بزرگ‌تر از یک به کسر

تبدیل اعداد اعشاری بزرگ‌تر از یک به کسر نیز مانند تبدیل اعداد اعشاری کوچک‌تر از یک و ساده است. برای این کار، می‌توانیم که عدد را بخوانیم و بنویسیم. برای مثال، عدد $$2.53$$ به‌شکل «دو و پنجاه و سه صدم» خوانده می‌شود. این عدد یک عدد مخلوط است که بخش صحیح آن $$2$$ و بخش کسری آن، $$0.53$$ است. همان‌طور که از بخش قبل یاد گرفتیم، $$0.53$$ به‌شکل $$\frac {53}{100}$$ نوشته می‌شود. در نهایت، عدد $$2.53$$ به‌شکل زیر خواهد بود:

$$2 . 53 = 2 \frac {53 } {100}$$

اکنون می‌توانیم این عدد مخلوط را به کسر تبدیل کنیم:

$$2 \frac {53 } {100} = 2+\frac {53} {100} = \frac {2\times 100}{100}+ \frac {53}{100}= \frac {200}{100}+\frac {53}{100}= \frac {200+53}{100}= \frac { 253 } {100}$$

برای آشنایی بیشتر با تبدیل عدد مخلوط به کسر، به آموزش «تبدیل عدد مخلوط به کسر — به زبان ساده + حل تمرین و مثال» مراجعه کنید.

به‌عنوان یک مثال دیگر، فرض کنید می‌خواهیم $$10.02$$ را به یک عدد کسری تبدیل کنیم. این عدد نیز از یک بخش صحیح $$10$$ و یک بخش اعشار $$0.02$$ تشکیل شده است. بنابراین یک عدد مخلوط داریم که بخش صحیح یا کامل آن $$10$$ و بخش کسری آن $$0.02$$ است. بنابراین، ابتدا بخش اعشاری عدد را به کسر تبدیل می‌کنیم. برای این کار، کافی است کسری بنویسیم که صورت آن عدد $$02$$ یا همان $$2$$ است و مخرج آن $$100$$، زیرا دو رقم سمت راست اعشار وجود دارد. بنابراین، $$0.02 = \frac 2 {100}$$. در نتیجه، عدد $$10 . 02$$ به‌صورت زیر نوشته می‌شود:

$$10 \frac 2 {100}$$

این عدد مخلوط را می‌توان به یک کسر تبدیل کرد:

$$10 \frac 2 {100} = 10 + \frac 2 {100} = \frac {10\times 100} { 100} + \frac { 2 } { 100 } = \frac {1000}{100}+\frac 2 {100} = \frac {1002} {100}$$

حال عدد اعشاری $$2.35$$ را در نظر بگیرید. این عدد را به صورت «دو و سی‌وپنج صدم» می‌خوانیم و آن را به شکل کسری زیر نمایش می‌دهیم:

$$2\frac {35}{100}$$

در واقع، $$2$$ واحد کامل و کسر $$\frac{35}{100}$$ را داریم.

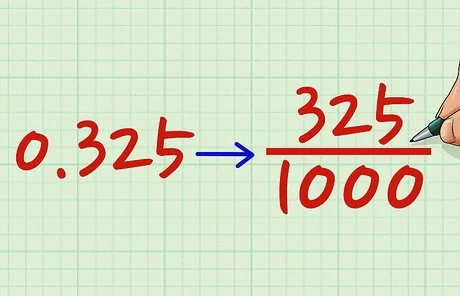
تبدیل اعداد اعشاری متناوب به کسر

اعداد اعشاری متناوب اعدادی هستند که پس از تعداد محدودی اعشار به پایان نمی‌رسند و برخی از ارقام خاص پس از اعشار در آن‌ها تکرار می‌شود. مثلاً $$1.333333...$$‌ یا $$2.545454...$$ اعداد اعشاری متناوب هستند. برای تبدیل هر اعشاری متناوب به عدد کسری، روش خاصی وجود دارد که برای درک آن مثالی را بررسی می‌کنیم.

فرض کنید می‌خواهیم عدد اعشاری $$0.77777...$$ را به کسر تبدیل کنیم.

ابتدا نام عدد اعشاری را $$x$$ می‌گذاریم. یعنی $$x=0.77777...$$.

سپس، عدد اعشاری را در $$10$$ ضرب می‌کنیم، یعنی:

$$10x=7.77777...$$

نکته: به این دلیل عدد را در $$10$$ ضرب کردیم که یک رقم $$7$$ بعد از اعشار تکرار شده است. مثلاً اگر $$0.717171...$$ را داشتیم، آن را در $$100$$ ضرب می‌کردیم، زیرا ارقام $$71$$ در آن تکرار شده بود.

اکنون $$x$$ را از $$10x$$ کم می‌کنیم. بنابراین، می‌توان نوشت:

$$10x - x = 7.7777...-0.7777... = 7$$

در نتیجه:

$$9x= 7$$

و

$$x = \frac 7 9$$

نکته: اعداد اعشاری متناوب را با یک خط روی عدد تکرارشونده نیز نشان می‌دهند. برای مثال، عدد $$2.535353...$$ را به‌شکل $$2.\overline {53}$$ نیز نشان داده می‌شود.

مثال‌های تبدیل اعداد اعشاری به کسر

در این بخش، مثال‌هایی از تبدیل اعداد اعشاری به کسر را بررسی می‌کنیم.

فیلم آموزش محاسبات سریع ریاضی – به زبان ساده + گواهینامه در فرادرس

کلیک کنید

مثال اول تبدیل اعداد اعشاری به کسر

عدد $$0.55$$ را به کسر تبدیل کنید.

حل: ابتدا کسر را تشکیل می‌دهیم. عدد صورت کسر همان اعداد سمت راست اعشار، یعنی $$55$$ است. مخرج نیز $$100$$ است، زیرا دو رقم سمت راست ممیز یا همان اعشار داریم و به همین دو صفر جلوی ۱ قرار داده‌ایم. عدد کسری به‌شکل زیر است:

$$0.55 = \frac {55}{100}$$

مثال دوم تبدیل اعداد اعشاری به کسر

عدد $$1.\overline {23}$$ را به کسر تبدیل کنید.

حل: ابتدا عدد را $$x$$ می‌نامیم. سپس آن را در $$100$$‌ ضرب می‌کنیم، زیرا دو رقم $$23$$ بعد از اعشار تکرار شده است:

$$100 x =100 \times 1 . \overline {23} = 123 .\overline {23}$$

اکنون، $$x$$ را از $$10 x$$ کم می‌کنیم و $$x$$ را به‌شکل کسری به‌دست می‌آوریم:

$$\begin {align} 100 x - x & = 123 .\overline {23}- 1 . \overline {23} \\ 99 x & = 122 \\ x & = \frac {122}{99} \end {align}$$

مثال سوم تبدیل اعداد اعشاری به کسر

عدد اعشاری $$4.43$$ را به کسر تبدیل کنید.

حل: اول از همه می‌دانیم که این عدد بزرگ‌تر از یک است و ابتدا آن را به‌شکل یک عدد مخلوط می‌نویسیم. بخش صحیح این عدد مخلوط $$4$$ است. برای تبدیل بخش اعشاری، یعنی $$0.43$$ به کسر، صورت را برابر با $$43$$ قرار می‌دهیم و مخرج را برابر با $$100$$، یعنی $$0.43 = \frac {43}{100}$$. بنابراین، عدد اعشاری به‌شکل زیر برابر با عدد مخلوط زیر است:

$$4.43 = 4 \frac {43 }{100}$$

این عدد مخلوط را می‌توان به‌صورت زیر به یک کسر تبدیل کرد:

$$4 \frac {43 }{100} = 4 + \frac {43 } { 100} = \frac {4\times 100}{100}+ \frac {43 } { 100} = \frac {400}{100}+\frac {43}{100} = \frac {443 } {100 }$$

مثال چهارم تبدیل اعداد اعشاری به کسر

عدد اعشاری $$25 . \overline {7}$$ را به کسر تبدیل کنید.

حل: عدد را برابر با $$x$$ در نظر می‌گیریم. با توجه به تکرار تک‌رقم $$7$$ در سمت راست آن، عدد را در $$10$$ ضرب می‌کنیم:

 $$10 x = 10 \times 25 . \overline {7} = 257. \overline { 7 }$$

اکنون $$x$$ را از $$10 x$$ کم می‌کنیم و مقدار کسری آن را به‌دست می‌آوریم:

$$\begin {align} 10 x - x & = 257. \overline { 7 } - 25. \overline { 7 } \\ 9 x & = 232 \\ x & = \frac {232} 9 \end {align}$$

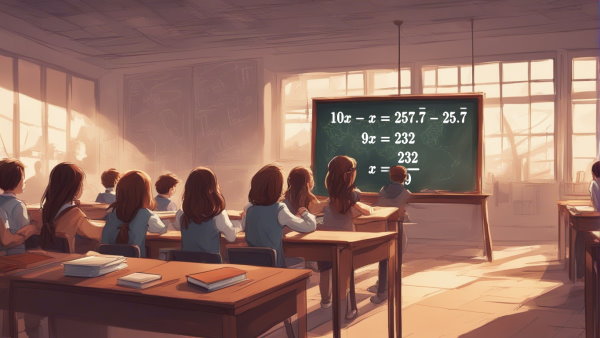
مثال پنجم تبدیل اعداد اعشاری به کسر

عدد اعشاری $$1.0045$$ را به کسر تبدیل کنید.

حل: این عدد یک عدد بزرگ‌تر از ۱ است و بنابراین، باید ابتدا آن را به‌شکل یک عدد مخلوط بنویسیم. برای این کار قسمت صحیح آن را داریم و باید بخش اعشاری را به کسر تبدیل کنیم. بنابراین، باید $$0.0045$$ را به کسر تبدیل کنیم و در کنار عدد کامل ۱ بنویسیم. بدین منظور، صورت کسر را برابر با $$0045$$ یا همان $$45$$ قرار می‌دهیم و با توجه به اینکه سمت راست اعشار چهار رقم داریم، مخرج برابر با $$10000$$ خواهد بود. این یعنی اینکه $$0.0045 = \frac {45 } {10000}$$. بنابراین، عدد $$1.0045$$‌به‌شکل عدد مخلوط زیر نوشته می‌شود:

$$1 . 0045 = 1 \frac { 45 } { 10000 }$$

اکنون این عدد مخلوط را به کسر تبدیل می‌کنیم:

$$1 \frac { 45 } { 10000 } = 1 + \frac {45} {10000} = \frac { 10000} {10000} +\frac {45}{10000} = \frac {10045}{10000}$$

مثال ششم تبدیل اعداد اعشاری به کسر

عدد $$0.28$$ را به کسر تبدیل کنید.

حل: این عدد بیست‌وهشت صدم است و می‌توانیم آن را به‌شکل زیر بنویسیم:

$$0.28 = \frac {28}{100}$$

این کسر را می‌توان ساده کرد و به‌شکل زیر نوشت:

$$\frac {28}{100} = \frac {4 \times 7}{4 \times 25 } = \frac {7} { 25 }$$

جمع‌بندی

در این آموزش از مجله فرادرس، با روش تبدیل عدد اعشاری به کسر و عدد مخلوط آشنا شدیم. همچنین، مثال‌های متنوعی از آن را همراه با راه‌حل بررسی کردیم.