تابع پله ای و خصوصیات آن | به زبان ساده

یک تابع روی مجموعه اعداد حقیقی را یک تابع پله ‌ای (Step Function) گویند، اگر آن را بتوان به صورت ترکیب خطی از توابع نشانگر روی یک فاصله متناهی تعریف کرد. به بیان دیگر تابع پله ای براساس تعداد زیادی از «توابع ثابت» (Constant Functions) نوشته می‌شود. از آنجایی که در ریاضیات گسسته و آمار و احتمال، تابع پله ای و خصوصیات آن اهمیت زیادی دارند، در این نوشتار از مجله فرادرس به بررسی این تابع پرداخته‌ایم.

برای روشن شدن بعضی از اصطلاحات این نوشتار بهتر است ابتدا رابطه و تابع از نگاه مجموعه‌ ها — به زبان ساده و مفاهیم تابع – به زبان ساده را بخوانید. همچنین مطالعه دامنه و برد تابع — به زبان ساده و تابع یک به یک و پوشا — به زبان ساده نیز خالی از لطف نیست.

تابع پله ای و خصوصیات آن

تابع $$f$$ از $${\cal{R}}$$ به $${\cal{R}}$$ را تابع پله ای (Step Function) می‌گویند اگر بتوان آن را به صورت زیر نمایش داد.

$$\large { \displaystyle f(x) = \sum \limits _{i = 0}^{n}\alpha _{i}\chi _{A_{i} }(x) }$$

فیلم آموزش حسابان ۱ – پایه یازدهم در فرادرس

کلیک کنید

بطوری که $$x$$ هر عددی حقیقی است. از طرفی $$n\geq 0$$ و $$\alpha_i$$ نیز اعداد حقیقی و $$\chi_A$$ نیز «تابع نشانگر» (Indicator Function) روی مجموعه $$A$$ بوده که به صورت زیر تعریف شده است.

$$\large {\displaystyle \chi _{A}(x) = {\begin{cases} 1 & {\text{ if }} x \in A \\ 0 & {\text{ if }} x \notin A \\ \end{cases}}}$$

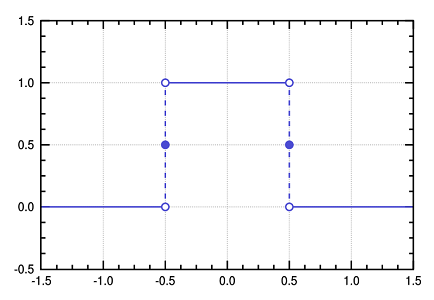
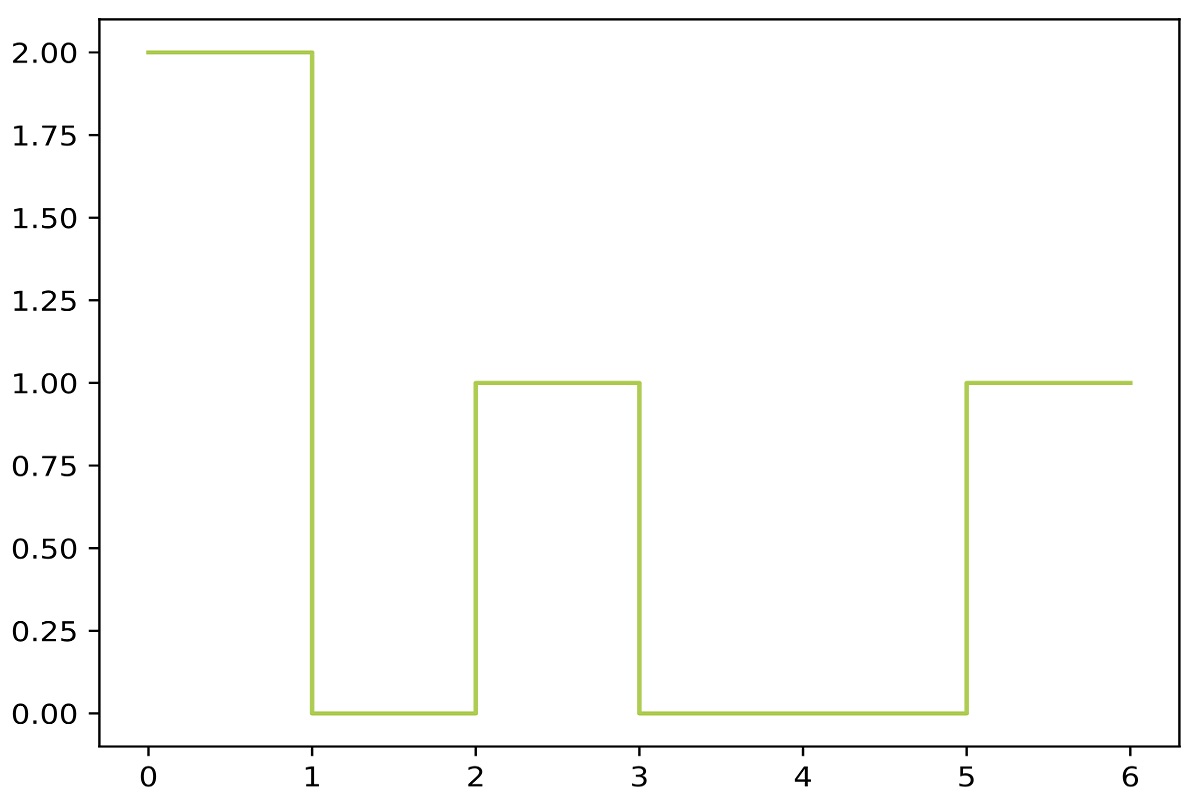
در تصویر ۱، نمونه‌ای از تابع پله ای که به تابع مستطیلی معروف است را مشاهده می‌کنید. واضح است در اینجا فاصله یا مجموعه‌ها به صورت زیر هستند.

$$\large A_1 = (- \infty , - 0.5 ) ,\;\;\; A_2 = [ - 0.5 , 0.5] , \;\;\; A_3 = (0.5 , \infty)$$

در تعریف ارائه شده، فاصله یا مجموعه $$A_i$$ را با خصوصیات زیر در نظر گرفته‌ایم.

• هر یک از این بازه یا مجموعه‌ها، «دو به دو جدا از هم» (Pairwise Disjoint) هستند. یعنی داریم: $$\large A_i \cap A_j = \emptyset , \;\; i \neq j$$

• این مجموعه یا فاصله‌ها، کل فضای اعداد حقیقی را پوشش می‌دهند. $$\large \cup_{i = 1}^n A_i = { \cal{R}}$$

نکته: اگر شرایط بالا وجود نداشته باشد، فاصله یا مجموعه‌های مختلفی برای بیان تابع مورد نظر وجود خواهد داشت. برای مثال تابعی پله‌ ای به صورت زیر را در نظر بگیرید:

$$ \large {\displaystyle f = 4\  \chi _{[ - 5 , 1 ) } + \ 3 \chi _{( 0 , 6 ) }} $$

این تابع را به کمک فاصله‌های دیگری نیز می‌توان ایجاد کرده و به صورت زیر نمایش داد.

$$ \large { \displaystyle f = 0 \ \chi _{( - \infty  , - 5 ) } + 4 \ \chi _{[ - 5 , 0 ] } + 7 \ \chi _{ ( 0 , 1 ) } + 3\  \chi _{ [ 1 , 6 ) } + 0 \ \chi _{ [ 6 , \infty ) } } $$

گاهی در تعریف، محدودیتی در نظر می‌گیرند که باید فاصله‌هایی به کار رفته در تعریف، از سمت راست باز باشند، یا امکان حضور تک نقطه‌ای‌ها هم در تعریف وجود داشته باشد. همچنین تابع پله‌ای در چنین نقاطی باید مقدار مجزا داشته باشد. از طرفی متناهی بودن این فاصله‌ها نیز گاهی نادیده گرفته می‌شوند. ولی با توجه به تعریفی که در این متن به آن اشاره شد، تابع پله ای باید به صورت اجتماع متناهی از توابع نشانگر با دامنه‌های مجزا نوشته شود.

چند نوع تابع پله ای

چند تابع مهم در ریاضیات با کاربرد در رشته برق و الکترونیک، از نوع تابع پله ‌ای محسوب می‌شوند که در این قسمت به معرفی بعضی از آن‌ها خواهیم پرداخت.

تابع جزء صحیح

براساس تعریفی که در این متن به آن اشاره شد، «تابع جزء صحیح» (Integer Part Function)، یک تابع پله‌ای در نظر گرفته نمی‌شود، زیرا تابع نشانگر آن براساس تعداد نامتناهی فاصله روی اعداد حقیقی ساخته شده است.

فیلم آموزش ریاضی 2 – پایه یازدهم علوم تجربی در فرادرس

کلیک کنید

ولی بعضی از ریاضیدانان با تغییر در تعریف تابع پله‌ای، چنین تابعی را نیز در گروه توابع پله‌ای قرار می‌دهند. در تصویر ۲، یک نمونه از نمودار تابع جزء صحیح را مشاهده می‌کنید که به صورت پله‌ای تغییر می‌کند.

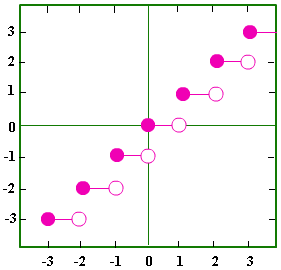
تابع علامت

«تابع علامت» (Sign Function) یکی از مثال‌های بارز برای تابع پله ای محسوب می‌شود. نماد این تابع به صورت $$\text {sgn}(x)$$ بوده و به شکل زیر معرفی شده است.

$$\large \text{sgn}(x) = \begin{cases} 1 & x > 0\\ 0 & x = 0 \\ -1 & x < 0 \end{cases}$$

تصویر ۳، نمودار چنین تابعی را نشان داده است. واضح است که دامنه آن همه اعداد حقیقی است ولی برد یا هم‌دامنه آن فقط مجموعه $$\{-1,0,1\}$$ است.

تابع پله ای هویساید

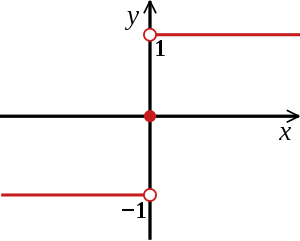
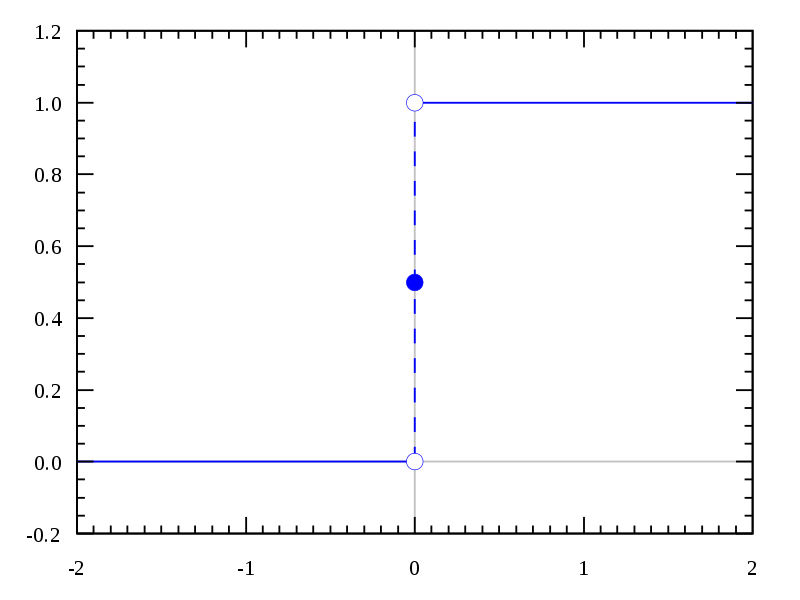
تابع $$H(x)$$ که توسط «اولیور هویساید» (Oliver Heaviside) ریاضیدان انگلیسی معرفی شده، نمونه‌ای دیگر از تابع پله ای است. مقدار $$H(x)$$ به ازای مقادیر منفی، برابر با صفر و برای مقادیر مثبت، مقدار ۱ را می‌گیرد. به این ترتیب می‌توان «تابع هویساید» (Heaviside Function) را معادل با تابع علامت دانست به طوری که تبدیل جابجایی و تغییر مقیاسی به شکل زیر رویش انجام شده باشد.

$$\large H (x) = \dfrac{ \text{sgn} ( x ) + 1) } {2}$$

نمودار تابع هویساید در تصویر 4، قابل مشاهده است. واضح است که این تابع در تک نقطه (یعنی x = 0) برابر با 0.5 در نظر گرفته شده، مهم آن است که مقدار تابع در این نقطه، متمایز با دو فاصله قبلی و بعدی یعنی مقادیر منفی و مثبت باشد.

تابع مستطیلی

یکی دیگر از انواع توابع پله‌ای به نام «تابع مستطیلی» (Rectangle Function) معروف است. چنین تابعی به شکل جمع سه تابع نشانگر نوشته می‌شود که برای نمایش مدل پالس و سینگال‌های دیجیتال به کار برده می‌شود.

فیلم آموزش ریاضی و آمار 2 – پایه یازدهم علوم انسانی در فرادرس

کلیک کنید

نمونه‌ای از این تابع را در تصویر 1، مشاهده کردید. ضابطه این تابع را به صورت زیر می‌توان نوشت.

$$\large {\displaystyle \operatorname {rect} (t) = \Pi (t) = \left\{ { \begin{array}{r l } 0 , & { \text{if }}| t | > { \frac {1}{2} } \\ { \frac {1}{2}} , & { \text{if }} | t | = { \frac {1}{2}} \\ 1 , & { \text{ if }} | t | < { \frac {1}{2}} \end{array}} \right.}$$

خواص تابع پله ای

بعضی از خواص جالب تابع پله ای در ادامه به صورت فهرست‌وار ذکر شده‌اند.

• جمع و ضرب دو تابع پله‌ای، باز هم یک تابع پله‌ای خواهد بود. همچنین حاصل ضرب یک عدد در تابع پله‌ای نیز تشکیل یک تابع پله‌ای خواهد داد. به این ترتیب با توجه به ویژگی‌های «فضای توپولوژیکی» (Topological Space) اعداد حقیقی، تابع پله‌ای روی مجموعه اعداد حقیقی، تشکیل یک جبر (Algebra) خواهد داد.
• هم‌دامنه یا برد تابع پله‌ای، یک مجموعه متناهی از مقادیر عددی است. در صورتی که طبق تعریف ارائه شده برای تابع پله‌ای، مجموعه‌های $$A_i$$ مجزا بوده و اجتماعشان اعداد حقیقی را بسازد، آنگاه می‌توان آن را به صورت زیر نیز معرفی کرد.

$$\large f(x) = a_i , x \in A_i$$

• انتگرال نامعین تابع پله‌ای یک «تابع خطی قطعه‌ای» (Piece-wise linear function) خواهد بود.
• «انتگرال لبگ» (Lebesgue Integration) برای تابع پله ای به شکل زیر قابل محاسبه است.

$$\large  {\displaystyle \textstyle f = \sum \limits _{ i = 0 }^{n} \alpha _{i}\chi _{A_{i}}} \rightarrow {\displaystyle \textstyle \int f \, dx = \sum \limits _{ i = 0 }^{n}\alpha _{i}\ell (A_{i})\,}$$

توجه داشته باشید که در رابطه بالا، $$ell(A)$$ طول بازه $$A$$ بوده و فرض می‌کنیم که طول هر یک از بازه‌های $$A_i$$ (اندازه لبگ مجموعه $$A_i$$) متناهی است.

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

به این ترتیب این الگو، پایه‌ای برای تشکیل انتگرال لبگ خواهد بود.

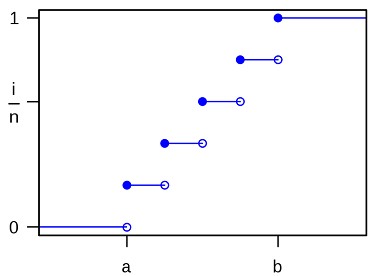
• «متغیر تصادفی گسسته» (Discrete Random Variable) دارای تابع توزیع تجمعی احتمال (Cumulative Distribution Function) به صورت یک تابع پله‌ای است. البته ممکن است تعداد گام‌ها یا پله‌ها، شمارا ولی نامتناهی باشد. در تصویر 5، تابع توزیع تجمعی «متغیر تصادفی گسسته یکنواخت» (Uniform Discrete Random Variable) را مشاهده می‌کنید که به فرم یک تابع پله‌ای نمایش داده شده است. در این نمودار، محور افقی مقادیر متغیر تصادفی و محور عمودی، مقدار تابع توزیع تجمعی احتمال (CDF) را نشان می‌دهد. فاصله یا ارتفاع نقاط پرش، نشانگر میزان احتمال در آن نقطه خواهد بود. توجه داشته باشید که در هر بازه روی محور افقی، مقدار احتمال تجمعی ثابت بوده و فقط در تک نقطه‌ها، پرش وجود دارد.

خلاصه و جمع‌بندی

در این نوشتار با دو شیوه معرفی تابع پله‌ای آشنا شدید. در وهله اول، حالت عمومی تابع پله‌ای بیان شد و در ادامه تابع پله‌ای خاصی به نام پله‌ای هویساید را مورد بررسی قرار دادیم. بعضی از ویژگی‌های مهم برای تابع پله ای نیز مورد بحث قرار گرفت. همانطور که در این متن خواندید، تابع پله ای و خصوصیات آن در بسیاری از مسائل ریاضیات مورد استفاده قرار می‌گیرد و بسیاری از توابع، نوع خاصی از تابع پله‌ای محسوب می‌شوند. در تئوری آمار و احتمال، متغیرهای تصادفی گسسته، دارای تابع توزیع تجمعی (CDF) به شکل پله‌ای هستند و از سمت راست پیوسته محسوب می‌شوند. متغیر تصادفی گسسته یکنواخت یا متغیر تصادفی با «توزیع هندسی» (Geometric Distribution)، از مثال‌هایی هستند که تابع توزیع تجمعی آن‌ها، پله‌ای است.