تابع ثابت و خصوصیات آن | به زبان ساده

در ریاضیات «تابع ثابت» (Constant Function)، به شکلی از تابع گفته می‌شود که به ازاء هر مقدار از دامنه آن، نتیجه یکسان و ثابتی حاصل شود. در نتیجه تابع ثابت، یک نگاشت از مجموعه اعداد حقیقی (موهومی) به یک مقدار (حقیقی یا موهومی) است. اغلب برای نمایش منحنی چنین تابعی، از یک خط راست و موازی محور افقی در «مختصات دکارتی» (Cartesian Coordinate) استفاده می‌شود. در این نوشتار به تابع ثابت و خصوصیات آن در ریاضیات می‌پردازیم.

به منظور آشنایی بیشتر با توابع و نحوه ترسیم آن‌ها بهتر است نوشتارهای رابطه و تابع از نگاه مجموعه‌ ها — به زبان ساده و رسم تابع — با مثال های حل شده را مطالعه کنید. همچنین خواندن مطالب دامنه و برد تابع — به زبان ساده و توابع جز صحیح — به زبان ساده نیز خالی از لطف نیست.

تابع ثابت و خصوصیات آن

اگر یک تابع به ازاء تغییر متغیرش، مقدار ثابتی داشته باشد، آن را تابع ثابت (Constant Function) می‌نامیم. به این ترتیب اگر دامنه (Domain) تابع ثابت، اعداد حقیقی باشد، هم‌دامنه (Codomain) آن یک عدد یا مقدار ثابت خواهد بود که ممکن است یک عدد حقیقی (یا موهومی) نیز باشد.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

به عنوان مثال در دنیایی واقعی برای تابع ثابت می‌توان به فروشگاهی اشاره کرد که همه اجناسش به یک قیمت فروخته می‌شود. به چنین فروشگاه‌هایی به اصطلاح «فروشگاه یک دلاری» می‌گویند.

تابع ثابت

فرض کنید تابعی در اختیار دارید که همه نقاط دامنه را به یک مقدار ثابت نگاشت می‌کند. چنین تابعی را می‌توان به صورت زیر معرفی کرد.

$$ \large f(x) = c ;\; \; \; \; \; \; \; x , c \in  {\cal{R}} $$

چنین تابعی را تابع ثابت در مجموعه اعداد حقیقی می‌شناسیم زیرا هم دامنه و هم برد آن زیر مجموعه‌ای از مجموعه «اعداد حقیقی» (Real Numbers) است.

نکته: از آنجایی که گاهی به جای $$f(x)$$ از $$y$$ ‌استفاده می‌شود، تابع ثابت را به صورت زیر نیز نشان می‌دهند.

$$ \large y = c $$

همانطور که دیده می‌شود، از متغیر $$x$$‌ در سمت راست رابطه، خبری نیست. در نتیجه مقدار تابع ثابت، بستگی به متغیر $$x$$ ندارد. به این ترتیب، مقادیر جدول زیر در تابع ثابت صدق می‌کنند.

واضح است که نمودار این تابع، محور عمودی را در نقطه $$(0,c)$$ قطع می‌کند.

نکته: اگر مقدار $$c=0$$ باشد، این تابع به صورت زیر نوشته شده و نمودار حاصل از آن، همان محور افقی خواهد بود.

$$ \large y = f(x) = 0  $$

برای مثال تابع $$y = f(x) = 4 $$ یک تابع ثابت است که نمودار آن را در تصویر ۱ مشاهده می‌کنید.

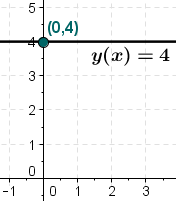
همانطور که در تصویر ۱ دیده می‌شود، با تغییر مقدار متغیر روی محور افقی، تابع ثابت بوده و تغییری روی محور عمودی رخ نمی‌دهد. به همین علت نمودار چنین تابعی به صورت یک خط افقی (موازی محور xها) بوده که محل برخورد آن با محور عمودی همان مقدار ثابت $$c$$، یعنی نقطه $$(0,4)$$ است.

نکته: گاهی به تابع ثابت، «تابع تباهیده» (Degenerate Function) در $$c$$ نیز می‌گویند. این اصطلاح، بخصوص برای «متغیر تصادفی تباهیده» (Degenerate Random Variable) به کار می‌رود که به ازاء هر پیشامد مقدار ثابتی دارد.

تابع ثابت و چند جمله‌ای‌ها

به یاد دارید که یک چند جمله‌ای درجه $$n$$‌ به شکل زیر نوشته می‌شود.

$$ \large P_n(x) = a_0 + a_1 x + a_2 x^2 + \ldots + a_nx^n $$

فیلم آموزش ریاضی و آمار ۲ – پایه یازدهم علوم انسانی در فرادرس

کلیک کنید

بنابراین اگر این چندجمله‌ای را در جمله اول ختم کنیم، یک تابع ثابت خواهیم داشت. پس در حقیقت تابع ثابت، یک چند جمله‌ای با درجه صفر است.

$$ \large P_n(x) = a_0 x^0 = a_0 = c $$

خصوصیات اصلی تابع ثابت

همانطور که تصویر ۱ نشان می‌دهد، تابع ثابت، هرگز محور افقی را قطع نمی‌کند، به جز در حالتی که $$y = f(x) =0 $$ باشد که در این صورت همه مقادیر $$x$$، ریشه‌های معادله خواهند بود. ولی در حالتی که $$c \neq 0 $$ تابع ثابت یا چند جمله‌ای درجه صفر، «ریشه» (Root) نخواهد داشت.

در ادامه به بعضی از خصوصیات جالب تابع ثابت اشاره خواهیم کرد.

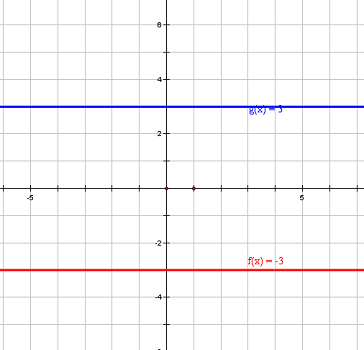
• تابع زوج (Even Function): تابع ثابت یک تابع زوج است. به معنی که با قرینه کردن مقدار متغیر، مقدار تابع تغییر نخواهد کرد. بنابراین نمودار این تابع نسبت به محور عمودی، قرینه است. پس قرینه هر مقدار متغیر برای چنین تابعی باز هم متعلق به دامنه بوده و برابر با مقدار تابع در همان مقدار است و در نتیجه روی منحنی آن تابع قرار می‌گیرد.

$$ \large f(-x) = f(x) = c $$

در تصویر ۲ دقت کنید. مقدار تابع $$f(x) = - 3$$ در نقطه ۵ و ۵- یکسان و برابر با ۳- است.

• مشتق تابع ثابت: براساس نحوه محاسبه مشتق، برای تابع ثابت، صفر مقدار مشتق خواهد بود. پس شیب نمودار تابع ثابت صفر بوده و هیچ پستی یا بلندی برای نمودار آن وجود ندارد.

$$ \large f'(x)=\dfrac{df}{dx} =\dfrac{dc}{dx} = 0 $$

• پیوستگی تابع ثابت: از آنجایی که دامنه تابع ثابت، اعداد حقیقی است و برای همه مقادیر آن، تعریف شده است، می‌توان نتیجه گرفت که این تابع روی دامنه‌اش، پیوسته خواهد بود. البته وجود مشتق برای چنین تابعی، نشانه ‌دیگری از پیوسته بودن آن است.
• غیرصعودی و نزولی بودن تابع ثابت: از آنجایی که مشتق تابع ثابت صفر است، چنین تابعی را نه می‌توان صعودی در نظر گرفت و نه نزولی. از طرفی مطابق با تصویر ۱ یا ۲، واضح است که تابع ثابت، یکنواخت و پیوسته محسوب می‌شود.
• انتگرال تابع ثابت: اگر انتگرال را سطح زیر منحنی تابع $$f(x)=a$$ در بازه دلخواه در نظر بگیریم، مطابق با تصویر ۳، این مساحت به شکل زیر حاصل می‌شود.

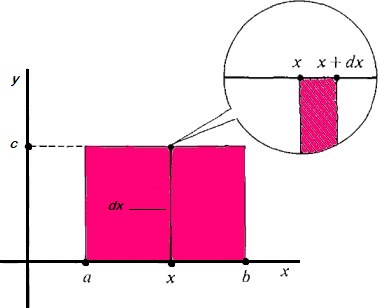
واضح است که مساحت این مستطیل، برابر با طول ($$b-a$$) در عرض یا ارتفاع ($$c$$) است. همین امر را به کمک انتگرال‌گیری نیز انجام می‌دهیم. طبق رابطه زیر انتگرال تابع ثابت روی فاصله $$a$$‌ تا $$b$$، برابر با حاصل‌ضرب مقدار ثابت در طول بازه است.

$$ \large \int_a^b f ( x ) dx = \int _a^b c dx = c x |^a_b = c ( b - a ) $$

ویژگی‌های تابع ثابت در نظریه مجموعه و توپولوژی

تابع ثابت، هم «حافظ ترتیب» (Order Preserving) و هم دارای خاصیت «ترتیب معکوس» (Order-Reversing) است. به طور معکوس، تابعی که این دو ویژگی را داشته باشد و دامنه آن یک «مشبکه» (Lattice)، باشد، تابع ثابت خواهد بود.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

هر تابع ثابت که «دامنه» (Domain) و «هم‌دامنه» (Codomain) آن مجموعه $$X$$ باشد، یک «تبدیل مونوید کامل» (Full Transformation Monoid) روی $$X$$ با «صفر چپ» (Left Zero) است.

نکته: صفر چپ، عنصری است که اگر از سمت چپ با عنصر دیگری طبق یک عملگر، ترکیب شود، تاثیری روی آن نخواهد داشت. به این ترتیب $$z$$ را عنصر صفر چپ می‌نامند اگر رابطه زیر تحت عملگر $$\cdot$$ برقرار باشد. همچنین تبدیل مونوید کامل، به مجموعه همه تبدیل‌ها روی $$X$$ گفته می‌شود.

$$ \large z \cdot s = z $$

به این ترتیب چنین تابعی یک تابع «خودتوان» (Idempotent) خواهد بود. به این معنی که ترکیب آن با هر تابعی، باز هم خودش را نتیجه می‌دهد. پس رابطه زیر نیز برای تابع ثابت بدست خواهد آمد.

$$ \large (f \circ f)(x)  = f ( f ( c ) )  = c = f(x) $$

از طرفی هر تابع ثابت در «فضای توپولوژیک» (Topological Space)، یک «تابع پیوسته» (Continuous) است.

خلاصه و جمع‌بندی

در این نوشتار در مورد تابع ثابت و خصوصیات آن توضیحاتی ارائه کردیم. مشخص شد که جنین تابعی رفتار ساده‌ای داشته و تابعی هموار، پیوسته، انتگرال و مشتق‌پذیر بوده و البته تابعی زوج است. اغلب تابع ثابت را برای ارائه مثال‌هایی ساده از خصوصیات دیگر توابع به کار می‌برند و در بعضی از حالات، با پدیده‌های مواجه هستید که تغییرات در آن‌ها به مانند تابع ثابت است. بنابراین با الگو گرفتن از تابع ثابت می‌توانیم رفتار آن‌ها را پیش‌بینی کنیم.