فرادرستابع برداری — به زبان ساده
پیش‌تر در بلاگ فرادرس مفاهیم معادله خط و معادله صفحه توضیح داده شدند. در این مفاهیم یک خط یا صفحه با استفاده از دو یا چند متغیر توصیف می‌شدند. متغیرهای مذکور اعدادی اسکالر بودند. در این مطلب قصد داریم تا مفهومی را مطرح کنیم که با استفاده از آن می‌توان موجودات هندسی را در قالب بردار توصیف کرد. این مفهوم همان تابع برداری یا تابع پارامتری است.
توجه داشته باشید که تابع برداری در انتگرال‌گیری توابع سطحی، خطی و هم‌چنین در قضایای گرین و استوکس کاربرد بسیاری دارد. البته در آینده در مورد مفاهیم مرتبط با توابع برداری همچون خمیدگی توابع برداری نیز بحث خواهیم کرد.
تابع برداری چیست؟
معمولا می‌توان هر هندسه‌ای را با استفاده از معادلات توصیف کرد. برای نمونه معادله دایره‌ای به شعاع r که در مبداء مختصات قرار گرفته را می‌توان به صورت زیر بیان کرد:
$$ x ^ 2 + y ^ 2 = r ^ 2$$
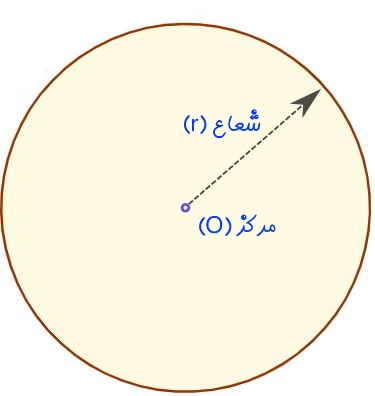
رابطه‌ی فوق در دستگاه مختصات کارتزینی و بر حسب دو متغیر x و y بیان شده است. حال این سوال پیش می‌آید که می‌توان همین دایره را بر حسب بردار بیان کرد؟ پاسخ مثبت است. در حقیقت می‌توان از مبدا به سمت هریک از نقاط روی منحنی برداری رسم کرده و نقاط بدست آمده را به هم متصل کرد. در ادامه نحوه بیان کردن این بردار توضیح داده خواهد شد.
تعریف تابع برداری
تابع برداری، رابطه‌ای برداری در فضای دو یا چند بعدی است که یک یا چند متغیر (مثلا u ،v یا t) را گرفته و خروجی آن یک بردار است. توجه داشته باشید که توابع برداری می‌توانند تک متغیره یا چند متغیره باشند. در این مطلب بیشتر توابع برداری تک متغیره را مورد بررسی قرار می‌دهیم. البته در انتهای این مطلب، به طور مختصر در مورد توابع برداری چند متغیره نیز صحبت خواهد شد.
تابعی برداری در فضای $$ { \mathbb { R } ^ 2 } $$ یا $$ { \mathbb { R } ^ 3 } $$ به صورت زیر نشان داده می‌شود.
$$ \overrightarrow r \left( t \right) = \left \langle { f \left ( t \right),g \left ( t \right)} \right\rangle \hspace {0.25in} \hspace{0.25in}\hspace{0.25in}\hspace { 0.25in } \overrightarrow r \left( t \right) = \left\langle { f \left( t \right),g \left ( t \right) , h \left( t \right)} \right\rangle $$
$$ f ( t ) , g ( t ) , h ( t ) $$ در حقیقت مولفه‌های این بردار هستند. در نتیجه برداری وجود دارد که مولفه‌هایش به شکلی وابسته به متغیر t تغییر کرده و مسیری خاص را توصیف می‌کند.
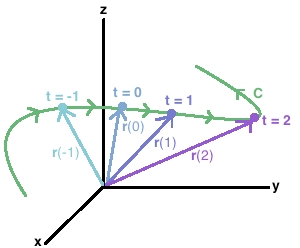
در شکل فوق، مسیر توصیف شده همان $$c$$ است که با تغییر نسبت به t شکل می‌گیرد. معمولا سوالاتی که در زمینه تابع برداری مطرح می‌شود، به این صورت است که در آن‌ها رابطه تابع برداری ارائه شده و بایستی منحنی آن بدست آورده شود.
به منظور رسم یک تابع برداری، در ابتدا تصور کنید که بردار r در هر لحظه t در یک نقطه قرار می‌گیرد. دلیل استفاده از واژه «لحظه» در جمله قبل درک بهتر مسئله است و الزامی وجود ندارد که متغیر درون تابع نشان دهنده زمان باشد. در مرحله بعد با کنار هم گذاشتن نقاط بدست آمده، مسیری منحنی شکل ایجاد خواهد شد. اجازه دهید تا در قالب مثال، رسم تابع برداری را توضیح دهیم.
مثال ۱
شکل توابع برداری ارائه شده در زیر را رسم کنید.
- $$ \overrightarrow r \left( t \right) = \left \langle { t , 1 } \right \rangle $$
- $$ \overrightarrow r \left( t \right ) = \left \langle { t , { t ^ 3 } - 1 0 t + 7 } \right \rangle $$
شکل تابع شماره ۱ بسیار ساده است. لذا می‌توان به ازای مقادیری از t، مولفه‌های تابع را محاسبه کرد. با رسم هرکدام از این مولفه‌ها، مسیر تابع برداریِ بیان شده، بدست خواهد آمد.
$$ \overrightarrow r \left ( { - 3} \right) = \left \langle { - 3 ,1 } \right \rangle \hspace { 0.25 in }\hspace {0.25in} \overrightarrow r\left( { - 1} \right) = \left\langle { - 1,1 } \right\rangle \hspace{ 0.25in } \hspace{0.25in }\overrightarrow r\left( 2 \right) = \left\langle { 2 ,1 } \right \rangle \hspace{0.25in}\hspace{0.25in}\overrightarrow r\left( 5 \right) = \left \langle {5,1} \right \rangle $$
بنابراین نقاط ارائه شده در ادامه، بخشی از منحنی برداری را تشکیل می‌دهند.
$$ \left( { - 3,1 } \right ) \hspace{ 0.25in}\hspace{0.25in}\left( { - 1,1 } \right)\hspace { 0.25in } \hspace {0.25in } \left( { 2 ,1 } \right ) \hspace { 0.25in } \hspace { 0.25in } \left( { 5 , 1 } \right ) $$
در حقیقت تابع برداری شماره ۱ توصیف کننده نمودار زیر است.
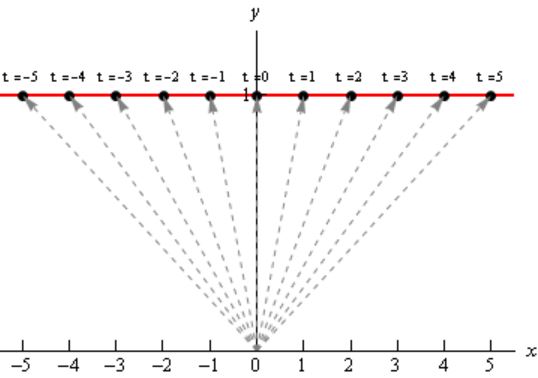
البته در ادامه خواهید دید که روش کلی ترسیم منحنی مرتبط با یک تابع برداری به این صورت نیست. در مورد تابع برداری شماره ۲ نیز مشابه با حالت اول ۴ نقطه را به صورت زیر بدست می‌آوریم.
$$ \overrightarrow r \left( { - 3} \right) = \left\langle { - 3,10} \right\rangle \hspace { 0.25in } \overrightarrow r \left( { - 1} \right) = \left \langle { - 1,16 } \right\rangle \hspace { 0.25in }\overrightarrow r\left( 1 \right ) = \left\langle { 1, - 2 } \right \rangle \hspace{0.25in}\overrightarrow r\left( 3 \right) = \left\langle { 3 , 4 } \right \rangle $$
با توجه به رابطه تابع، روشن است که شکل منحنی آن همچون تابع شماره ۱ ساده نیست. در ادامه منحنی این تابع نیز نشان داده شده است.
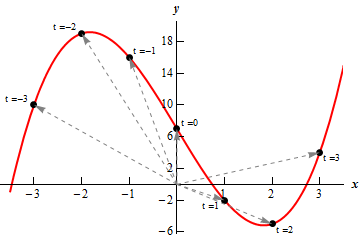
هر دو تابع ارائه شده در مثال ۱ دارای ساختاری به صورت $$ \overrightarrow r \left ( t \right ) = \left \langle { t , g \left ( t \right ) } \right \rangle $$ هستند. در ادامه مثال‌هایی را مطرح می‌کنیم که با استفاده از آن‌ها می‌توان نمودار مرتبط با یک منحنی را به شکلی ساده‌تر حدس زد.
همان‌طور که در بالا نیز بیان شد، مولفه‌های یک تابع برداری نشان دهنده متغیرهای یک تابع اسکالر هستند. برای نمونه تابعی برداری با رابطه $$ \overrightarrow r \left( t \right ) = \left \langle { f \left ( t \right ) , g \left ( t \right ) } \right \rangle $$ را در نظر بگیرید. در این رابطه مولفه‌ها در حقیقت x و y یک نمودار دوبعدی را نشان می‌دهند. در حقیقت می‌توان گفت:
$$ x = f \left ( t \right ) \hspace { 0.25 in } y = g \left( t \right ) \hspace { 0.25in } z = h \left ( t \right ) $$
حال می‌توان با حذف کردن پارامتر‌ها، متغیرهای x و y را به یکدیگر مرتبط کرده و به تابعی در دستگاه x-y دست یافت. احتمالا با مطالعه مثال‌هایی که در ادامه ارائه شده، مفاهیم بیان شده را بهتر درک خواهید کرد.
مثال ۲
نمودار تابع برداری $$ \overrightarrow r \left ( t \right ) = \left \langle { 2 - 4 t , - 1 + 5 t , 3 + t } \right \rangle $$ را رسم کنید.
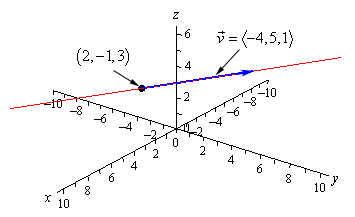
شاید در ابتدا نمودار رابطه فوق پیچیده به نظر برسد. اما این تابع، تنها نشان دهنده یک خط در فضای سه‌بعدی است. شاید اگر این خط به صورت زیر بازنویسی شود، رسم نمودار نیز آسان‌تر شود.
$$ \overrightarrow r \left ( t \right ) = \left \langle { 2 , - 1 , 3 } \right \rangle + t \left \langle { - 4,5,1 } \right \rangle $$
با توجه به شکل بیان شده در بالا، می‌توان فهمید که این رابطه نشان دهنده خطی است که از نقطه $$ \left( { 2 , - 1 , 3 } \right ) $$ عبور کرده و موازی بردار $$ \overrightarrow v = \left \langle { - 4 , 5 , 1 } \right \rangle $$ است. بنابراین تنها با مشخص کردن نقطه‌ی مذکور در دستگاه مختصات سه‌بعدی و ترسیم خطی در راستای بردار v، خط زیر بدست خواهد آمد.
مثال ۳
نمودار تابع برداری زیر را رسم کنید.
$$ \overrightarrow r \left ( t \right ) = \left \langle { 2 \cos t , 2 \sin t , 3 } \right \rangle $$
بدیهی است که رابطه فوق نیز منحنی سه‌بعدی را نشان می‌دهد؛ چرا که این منحنی دارای سه مولفه است. مولفه‌های این نمودار به صورت زیر هستند:
$$x = 2\cos t\hspace{0.25in}\hspace{0.25in}y = 2\sin t\hspace{0.25in}\hspace{0.25in}z = 3$$
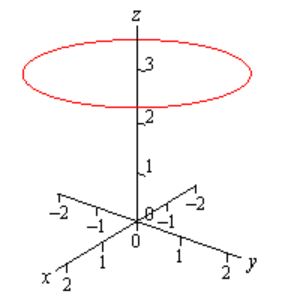
در رابطه فوق متغیر z ثابت بوده و به متغیرهای x و y وابسته نیست. از طرفی رابطه بین x و y را می‌توان به صورت زیر بدست آورد:
$$ x ^ 2 + y ^ 2 = (2 \cos t ) ^ 2 + (2 \sin t )^2 = 4$$
با توجه به رابطه فوق، تابع برداری مفروض، دایره‌ای به شعاع ۲ و مبدا (0,0) را نشان می‌دهد. البته دقت کنید چرا که این دایره در فاصله z=3 از مبدا قرار گرفته است.
مثال ۴
نمودار تابع برداری $$ \overrightarrow r \left ( t \right ) = \left \langle { 4 \cos t , 4 \sin t , t } \right \rangle $$ را رسم کنید.
واضح است که اگر مقدار z ثابت بود، نمودار مشابه با مثال ۳ میشد. اما در این حالت شکل نمودار در صفحه x-y دایره بوده و در راستای z به صورت خطی صعود می‌کند. با این دو فرض، شکل نمودار به صورت زیر بدست می‌آید.
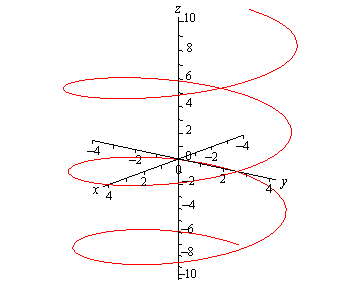
همان‌طور که دیدید شکل نمودار به صورت یک مارپیچ سه بعدی است.
تابع برداری دو متغیره
همان‌طور که در ابتدای این مطلب نیز ذکر شد، در این مطلب بیشتر در مورد توابع برداری تک متغیره صحبت می‌شود. این در حالی است که می‌توان توابع برداری دومتغیره را نیز ارائه داد. توجه داشته باشید که معمولا از توابع برداری دو متغیره به منظور توصیف صفحه استفاده می‌شود. در این مطلب تنها به ارائه یک مثال در مورد توابع برداری دو متغیره بسنده کرده و در آینده توابع برداری دو متغیره را به تفصیل توضیح خواهیم داد.
مثال ۵
سطح توصیف شده توسط بردار $$ \overrightarrow r \left ( { u , v } \right ) = u \,\overrightarrow i + v \,\overrightarrow j + \left ( { { u ^ 2 } + { v ^ 2 } } \right) \overrightarrow k $$ به چه صورت است؟
همان‌طور که در رابطه ارائه شده می‌بینید، از دو متغیر به منظور بیان تابع برداری استفاده شده است. بنابراین تابع مذکور برداری است که نقاط آن نشان دهنده صفحه است. به منظور بدست آوردن صفحه، می‌توان شکل تابع را بر حسب (x,y,z) بدست آورده، سپس صفحه تابع را حدس زد. مولفه‌های تابع برداری ارائه شده برابرند با:
$$ x = u \hspace { 0.25in } \hspace { 0.25in } y = v \hspace{ 0.25in } \hspace { 0.25in } \hspace { 0.25 in } z = { u ^ 2 } + { v ^ 2 } $$
با جایگذاری x=u و y=v در رابطه فوق، به رابطه $$ z = x ^ 2 + y ^ 2 $$ می‌رسیم. این رابطه، سطحی را نشان می‌دهد که با افزایش مقادیر x و y در آن شعاع دایره نیز به‌صورت نمایی افزایش می‌یابد.
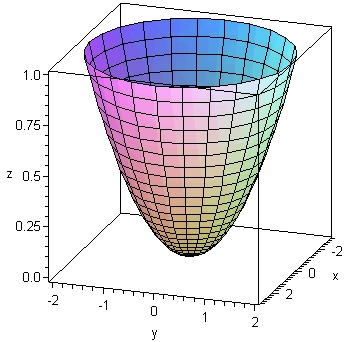
سطح فوق معروف به سهمی‌گون بیضی‌گون است.
در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های ریاضی و فیزیک
- مجموعه آموزش‌های ریاضی
- خمیدگی توابع برداری — به زبان ساده
- قضیه گرین -- به زبان ساده
- قضیه استوکس -- به زبان ساده
- انتگرال سطحی — از صفر تا صد
^^
ای کاش میشد که برای این مبحث فیلمی تهیه می کردید.
عالی یه دوره فرادرس ریاضی پایه تا پیشرفته برای علامندان ضبط کنین عالی میشد
با سلام؛
برای مشاهده فیلم‌های آموزشی مرتبط با ریاضیات پایه و دانشگاه، از لینک‌های زیر کمک بگیرید.
مجموعه فیلم آموزش ریاضیات
مجموعه آموزش دروس دبیرستان
با تشکر از همراهی شما با مجله فرادرس
با درو متشکر
عالیییییی