برازش حداقل مربعات – به زبان ساده
برازش منحنی به برازش یک تابع از پیش تعریف شده اطلاق میشود که متغیرهای مستقل و وابسته را به یکدیگر مربوط میکند. گام اول در محاسبه بهترین منحنی یا خط، پارامتری کردن تابع خطا با استفاده از متغیرهای اسکالر کمتر، محاسبه مشتق خطا نسبت به پارامترها و در نهایت محاسبه پارامترهایی است که تابع هزینه خطا را کمینه میکنند. در روش «برازش حداقل مربعات» (Least-Square Fitting)، به جای آنکه از قدر مطلق خطا استفاده کنیم، مربع آن را در نظر میگیریم، زیرا در این صورت، دادههای دور از منحنی برازش شده با بالا بردن مقیاس توسط اندازه خطا جریمه میشوند. این یعنی اینکه برای مثال، انحراف ۲ به اندازه ۴ در نظر گرفته خواهد شد.
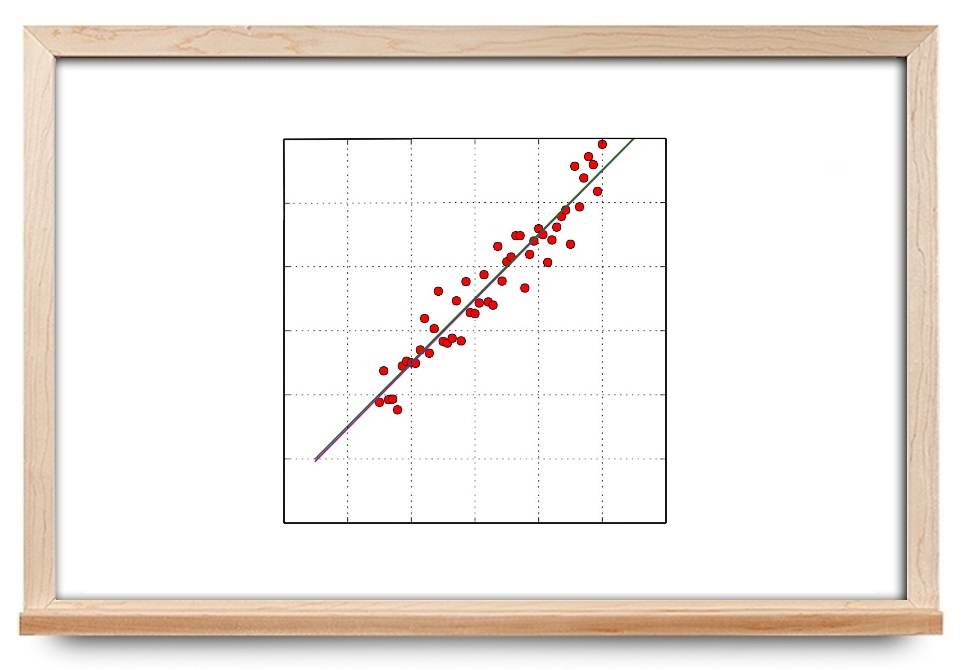
بنابراین، کمینهسازی مجموع مربعات خطا منجر به برازشی میشود که خطاهای کوچکتری را در نظر میگیرد. رایجترین روش برای تعیین پارامترهایی که منحنی را مشخص میکنند، تعیین جهت کاهش خطا و یک گام کوچک در آن جهت و تکرار فرایند تا جایی است که به همگرایی برسیم. این فرایند حل تکراری پارامترها به عنوان روش «گرادیان کاهشی» (Gradient Descent) نیز شناخته میشود. در این آموزش، از محاسبات ماتریسی پایه استفاده میکنیم و آنها را برای به دست آوردن پارامترها به منظور بهترین برازش منحنی به کار میگیریم. در حالتهای خاص، جایی که تابع پیشبین در پارامترهای مجهول خطی است، یک فرم بسته از جواب شبهوارون (Pseudoinverse) را میتوان به دست آورد. در این آموزش، هر دو راهحل گرادیان نزولی و شبهوارون را برای محاسبه پارامترهای برازش بررسی میکنیم.
مشتق مرتبه اول نسبت به اسکالر و بردار
در این بخش اصول حسابان ماتریسی را بیان کرده و نشان میدهیم که چگونه باید از آن برای بیان مشتقات یک تابع استفاده کرد. ابتدا، چند نماد را معرفی میکنیم: یک اسکالر برای حرف انگلیسی کوچک و عادی مثل ، یک بردار با حرف کوچک انگلیسی و پررنگ مثل و یک ماتریس با حرف انگلیسی بزرگ و پررنگ مثل .
مشق تابع اسکالر نسبت به بردار
مشتق یک تابع اسکالر نسبت به یک بردار، برداری از مشتق تابع اسکالر نسبت به تک تک درایههای بردار است. بنابراین، برای تابع از بردار داریم:
به طور مشابه، مشتق ضرب نقطهای دو بردار و در را میتوان به صورت زیر نوشت:
به طور مشابه، داریم:
نکته: اگر تابع اسکالر بوده و برداری که نسبت به آن مشتق میگیریم دارای بعد باشد، آنگاه بعد مشتق است.
مشتق تابع برداری نسبت به اسکالر
مشتق یک تابع برداری نسبت به یک اسکالر، برداری از مشتق درایههای تابع برداری نسبت به متغیر اسکالر است. بنابراین، برای تابع از متغیر ، خواهیم داشت:
اگر بعد تابع برداری باشد، آنگاه مشتق آن نسبت به یک اسکالر دارای بعد خواهد بود.
مشتق تابع برداری نسبت به بردار
مشتق یک تابع برداری نسبت به یک بردار، ماتریسی است که درایههای آن مشتق درایههای تابع برداری نسبت به درایههای بردار هستند. بنابراین، برای تابع برداری از بردار ، داریم:
نکته: اگر تابع برداری با ابعاد بوده و برداری که نسبت به آن مشتق میگیریم، دارای بعد باشد، آنگاه بعد مشتق خواهد بود.
برای حالت خاصی که داشته باشیم:
مشتق به صورت زیر است:
برازش حداقل مربعات
مثالی که مفاهیم مذکور بالا را میتوان به آن اعمال کرد، برازش حداقل مربعات خط است. در برازش حداقل مربعات خط، هدف یافتن بردار وزنها به گونهای است که خطای بین مقدار هدف و پیشبینیهای یک مدل خطی را کمینه کند.
شرح مسئله
تعداد نقطه آموزش را در نظر بگیرید که برای هر ، بردار را به یک خروجی اسکالر نگاشت میدهد. هدف یافتن بردار خطی به گونهای است که خطای زیر کمینه شود:
که در آن، برابر با اُمین درایه و عرض از مبدأ است.
حل: بردار مستقل را با قرار دادن درایه جدید ۱ به انتهای آن و بردار را با قرار دادن در انتها افزایش میدهیم. در نتیجه، تابع هزینه به صورت زیر در خواهد آمد:
تابع هزینه بالا را میتوان به عنوان یک ضرب نقطهای از بردار خطا نوشت:
که در آن، ماتریسی با اندازه در و یک بردار با طول و برداری به طول است.
بنابراین، اکنون تابع هزینه به صورت زیر خواهد بود:
با اعمال ترانهاده در فرمول بالا، خواهیم داشت:
لازم به ذکر است که همه جملات در معادله بالا اسکالر هستند. با مشتقگیری نسبت به ، خواهیم داشت:
روش گرادیان کاهشی
کمینه زمانی به دست میآید که مشتق بالا برابر با صفر باشد. رایجترین روش مورد استفاده یک راه حل مبتنی بر گرادیان کاهشی است که در آن، از یک حدس اولیه برای شروع کرده و آن را به صورت زیر بهروز میکنیم:
میتوان صحیح بودن محاسبه تحلیلی مشتق را بررسی کرد. این کار با استفاده از روش تفاضل مرکزی قابل انجام است.
روش تفاضل مرکزی روش مناسبی است، زیرا این روش دارای خطای است، در حالی که خطای روش تفاضل مستقیم است. از سری تیلور نیز میتوان برای این منظور استفاده کرد.
روش شبهوارون
یک روش دیگر، محاسبه مستقیم بهترین جواب با صفر قرار دادن مشتق اول تابع هزینه است:
با اعمال ترانهاده، مقدار به صورت زیر به دست میآید:
مثال برازش حداقل مربعات خط
در این بخش، تعدادی داده تولید کرده و روشهای ارائه شده در بالا را به آنها اعمال میکنیم. میخواهیم بهترین خط برازش کننده را با استفاده از روشهای گرادیان کاهشی و شبهوارون محاسبه و آنها را با هم مقایسه کنیم.
دادهها را در پایتون به صورت زیر تولید میکنیم:
این دادههای نویزی به صورت زیر هستند.
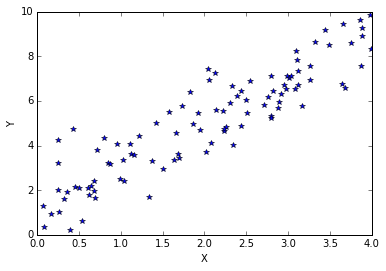
برازش حداقل مربعات با استفاده از گرادیان کاهشی
همانطور که گفتیم، روش گرادیان کاهشی برای محاسبه بهترین برازش خط به کار میرود. در این روش از یک مقدار کوچک نرخ یادگیری استفاده میشود. انتخاب نرخ یادگیری خود بحث مفصلی دارد که در اینجا از بیان آن صرفنظر میکنیم. در اینجا فرض میکنیم ۰٫۰۰۰۰۵ انتخاب مناسبی برای نرخ یادگیری باشد. گرادیان با استفاده از معادلهای که پیشتر بیان کردیم، قابل محاسبه است و وزنها (یا ضرایب) در هر مرحله ذخیره میشوند.
برنامههای زیر در پایتون، پیادهسازی روش گرادیان کاهشی را نشان میدهند.
جواب حاصل از اجرای برنامه فوق به صورت نوشتاری و شکل زیر هستند:
Iteration # 0 Numerical gradient: [-1255.13,-505.70] Analytical gradient:[-1255.13,-505.70] Iteration # 50 Numerical gradient: [-264.16,-115.18] Analytical gradient:[-264.16,-115.18] Iteration # 100 Numerical gradient: [-53.40,-31.67] Analytical gradient:[-53.40,-31.67] Iteration # 150 Numerical gradient: [-8.69,-13.53] Analytical gradient:[-8.69,-13.53] Iteration # 200 Numerical gradient: [0.68,-9.32] Analytical gradient:[0.68,-9.32] Gradient descent took 0.006886 s
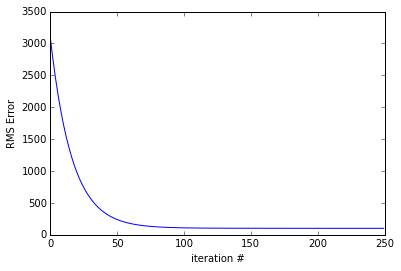
حال برای درک بهتر، شکلهای خط برازش شده را برای تکرارهای مختلف رسم میکنیم. برنامه و شکلها در ادامه آورده شدهاند.
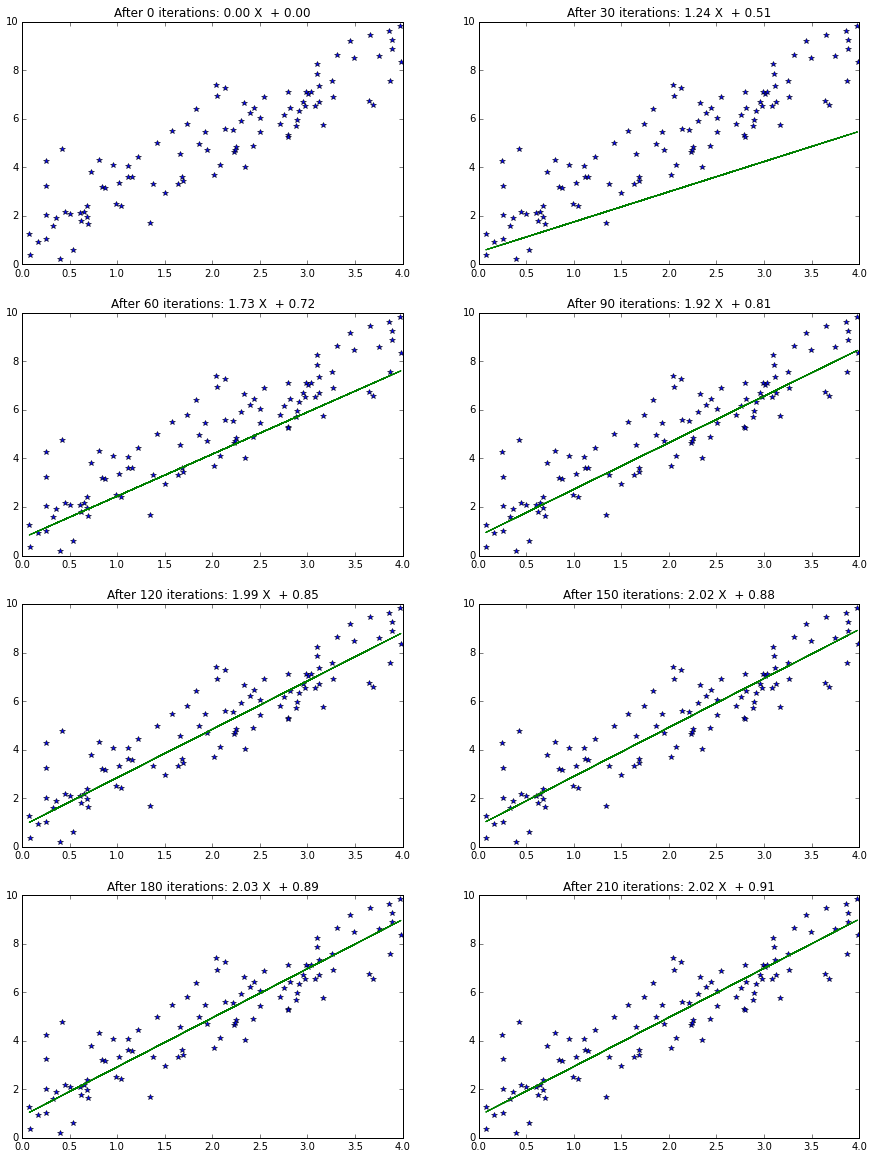
برازش حداقل مربعات با روش شبهوارون
محاسباتی را که در بالا برای روش شبهوارون بیان کردیم، به صورت زیر در پایتون پیادهسازی میشود:
شکل زیر، حاصل از اجرای این برنامه است.
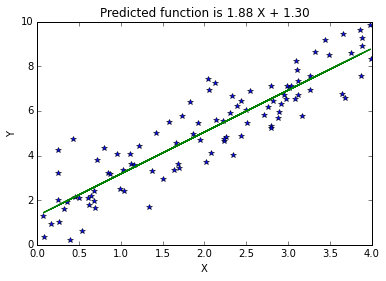
برازش دایره
مجموعه نقاطی را در نظر بگیرید که میخواهیم یک دایره را برای آنها برازش کنیم. همانطور که میدانیم، دایره یک تابع خطی نیست. البته، معادله یک دایره را میتوان طوری بازنویسی کرد که برحسب پارامترهای مجهول (یعنی محل مرکز و شعاع) خطی باشد. معادله دایرهای را در نظر بگیرید که مرکز آن و شعاعش است:
با بسط معادله بالا و مرتبسازی آن، داریم:
معادله بالا دارای سه مجهول ، و است و معادله یک دایره برحسب این سه پارامتر خطی است.
و را به صورت زیر تعریف میکنیم:
بنابراین، معادله برازش دایره بالا را میتوان به صورت زیر نوشت:
که در آن، .
برنامه پیادهسازی برازش دایره در پایتون به صورت زیر است:
شکل زیر، نتیجه اجرای این برنامه است.
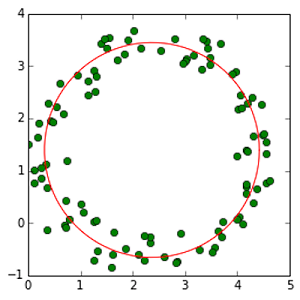
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای محاسبات عددی
- آموزش محاسبات عددی (مرور و حل مساله)
- مجموعه آموزشهای دروس ریاضیات
- آموزش محاسبات عددی با MATLAB
- بیش برازش (Overfitting)، کم برازش (Underfitting) و برازش مناسب — مفهوم و شناسایی
- آزمون نیکویی برازش (Goodness of Fit Test) و استقلال — کاربرد توزیع کای۲
- روش ژاکوبی — به زبان ساده
^^













سلام ممنون از آموزشتون
در قسمت شرح مسئله تابع خطایی که باید کمینه شود از کجا آمده است و اینکه چرا xij داریم درحالی که x یک بردار است و باید xi باشد؟؟
سلام بر استاد عزیز
واقعا عالی بود، خیلی خوب مبحث رو برای من باز کردید. خیلی مثالها عالی بودن، گفتم حتما از استاد عزیز، جناب حمیدی تشکر کنم.
از تیم فرادرس بخاطر سایت خوبتون ممنون و سپاسگزارم.
دستتون طلا
شاد و سلامت باشید.
امید زندی عزیز! دمت گرم و تشکر از تدریس خوبت
سلام و سپاس از زحمات گروه فرادرس
و تشکر از استاد زندی با نحوه ی عالی تدریسشون
اگر ما یک معادله دیفرانسیل داشته باشیم و بخواهیم جواب تقریبی آن را با استفاده از روش حداقل مربعات خطا(LSE) و یا روش گالرکین بدست بیاوریم چگونه بدست میاید؟
با فرض این که جواب تحلیلی یا دقیق آن را نمی دانیم.
اگه امکانش هست از این دو روش هم آموزش تهیه کنید.
البته بیشتر دنبال کدش هستم!:)
با تشکر