القای مغناطیسی — به زبان ساده

القای مغناطیسی توسط «مایکل فارادی» (Michael Faraday) در سال 1831 کشف شد، اندکی بعد ماکسول آن را به صورت ریاضی بیان کرد و به عنوان قانون القای فارادی شناخته شد. فارادی سه آزمایش را برای درک القای الکترومغناطیسی طرحریزی کرد. در حال حاضر قانون فارادی کاربردهای بسیار مهمی دارد و در ژنراتورها، ترانسفورماتورها و غیره کاربرد دارد. در این مطلب قصد داریم در مورد القای مغناطیسی و اثرات ناشی از آن و کاربردهای القای مغناطیسی در زندگی روزمره مطالبی را بیان کنیم.
القای مغناطیسی چیست؟
القای مغناطیسی که به آن القای الکترومغناطیسی نیز گفته میشود، به تولید ولتاژ (یا EMF) در یک رسانای الکتریکی که در داخل یک میدان مغناطیسی متغیر قرار گرفته اشاره دارد. یعنی در یک میدان مغناطیسی در یک سطح محصور با تغییر میدان مغناطیسی ولتاژ تغییر میکند. مطابق قانون فارادی در یک مدار بسته نیروی الکتریکی القایی برابر با تغییر شار مغناطیسی محصور شده توسط مدار است.
شار مغناطیسی برابر با کل میدان مغناطیسی است که از یک منطقه مشخص عبور میکند. این کمیت یک ابزار مفید برای کمک به توصیف اثرات نیروی مغناطیسی بر آن منطقه است.
اندازه شار مغناطیسی وابسته به مساحتی است که انتخاب شده، اگر میدان مغناطیسی را به صورت خطوط میدان که از یک مساحت مشخص عبور میکند در نظر بگیریم، هر خط میدانی که از منطقه عبور میکند در مقدار شار مغناطیسی تاثیر دارد. همچنین زاویهای که هر خط میدان با محور عمود بر سطح میسازد نیز مهم است. هنگام محاسبه شار مغناطیسی تنها عناصری از میدان که با بردار عمود بر سطح موازی هستند را در نظر میگیریم. خطوط دیگر میدان با توجه به زاویهشان با خط نرمال در مقدار شار تاثیر دارند ولی تاثیر آنها کمتر است تا زمانی که خطوط شار بر بردار عمود بر سطح یا بردار نرمال در حالت عمود قرار میگیرند. در این حالت این خطوط میدان بر شار مغناطیسی تاثیری ندارند.
اگر یک سطح صاف ساده با مساحت $$A$$ را در نظر بگیریم که زاویه بین بردار نُرمال سطح و خطوط میدان مغناطیسی $$\theta$$ باشد شار مغناطیسی برابر است با
$$\large\phi = B A \cos {\theta}$$
اگر سطح بر خطوط میدان عمود باشد، شار مغناطیسی برابر با $$\phi=BA$$ است. دقت کنید که هر سطح یک بردار نُرمال دارد که عمود بر سطح و به سمت خارج سطح رسم میشود، مانند تصویر زیر

شکل زیر نمونهای از یک سطح تخت را در دو زاویه مختلف با یک میدان مغناطیسی و شار مغناطیسی حاصل نشان میدهد .
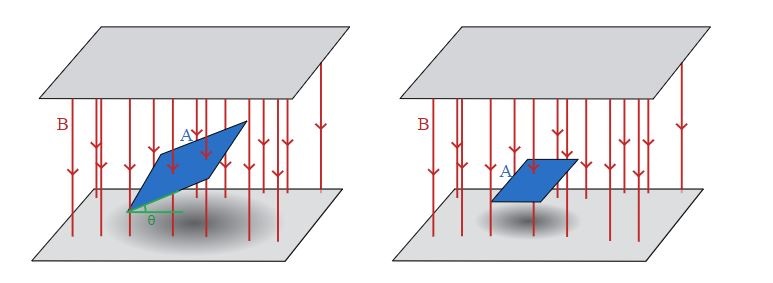
اگر در تصویر سمت چپ (۲) زاویه $$\theta$$ برابر با ۲۵ درجه باشد، شار مغناطیسی $$9\%$$ از تصویر سمت راست کوچکتر خواهد بود. با افزایش $$\theta$$ این اختلاف بیشتر میشود. تا جایی که در $$\theta=90$$ شار مغناطیسی صفر میشود.
واحد $$SI$$ شار مغناطیسی «وِبِر» (Weber) به نام فیزیکدان آلمانی و مخترع مشترک تلگراف، «ویلهلم وبر» (Wilhelm Weber)، و دارای نماد $$Wb$$ است.
از آنجا که شار مغناطیسی فقط روشی برای بیان میدان مغناطیسی در یک منطقه معین است میتوان آن را با مغناطیسسنج به همان روش میدان مغناطیسی اندازهگیری کرد.
فرمولهای القای مغناطیسی
از قانون فارادی میدان الکترومغناطیسی القا شده در یک مدار بسته برابر است با
$$\large \epsilon = -\frac {d \phi_ {b}} {dt}$$
در این رابطه $$\phi_ {b}$$ شار مغناطیسی، t زمان و $$\epsilon$$ ولتاژ القایی است. توجه داشته باشید:
$$\large \phi _ {b} = \oint \vec {B} \cdot d \vec{s}$$
که B میدان مغناطیسی و $$ds$$ بخش کوچکی از سطح است. در یک سیمپیچ با $$N$$ دور القای مغناطیسی برابر است با:
$$\large \epsilon = - N \frac {d \phi_ {b}} {dt}$$
این معادله جهت جریان القایی را تعیین میکند و از قانون پایستگی انرژی پیروی میکند.
برای یک رسانای در حال حرکت ولتاژ القایی برابر است با
$$\large \epsilon = Blv \sin\theta$$
که $$l$$ طول رسانا، $$v$$ سرعت رسانا و $$\theta$$ زاویه بین میدان مغناطیسی و جهت حرکت است. برای درک بهتر موضوع به حل مثالی مربوط به القای مغناطیسی میپردازیم.

مثال ۱: اگر شار مغناطیسی متصل به یک سیم پیچ از $$12\times 10^{-3}$$ وبر به $$6\times 10^{-3}$$ وبر در $$0.01$$ ثانیه تغییر کند، مقدار ولتاژ القایی را محاسبه کنید.
جواب: مقدار ولتاژ القایی از رابطه $$\large \epsilon = -\frac {d \phi_ {b}} {dt}$$ به دست میآید و برابر است با:
$$\large \epsilon =- \frac {d \phi_ {b}} {dt}=-\frac{(6\times 10^{-3}-12\times 10^{-3})}{0.01}=\frac{6\times 10^{-3}}{10^{-2}}=0.6\ (V)$$
همانطور که ملاحظه میکنید با تغییر شار مغناطیسی که وابسته به میدان الکتریکی در زمان است، در سیستم ولتاژ ایجاد میشود.
کاربرد القای مغناطیسی
امروزه از القای مغناطیسی برای تأمین انرژی بسیاری از دستگاههای الکتریکی استفاده میشود. یکی از مشهورترین موارد استفاده در ژنراتورهای الکتریکی (مانند سدهای مربوط به تولید برق) است که در آن از قدرت مکانیکی برای انتقال میدان مغناطیسی از سیم پیچها برای تولید ولتاژ استفاده میشود.










