اصل ارشمیدس — به زبان ساده

وقتی از یک وان یا استخر آب گرم خارج می‌شوید، احتمالاً به طور عجیبی در دستان خود احساس سنگینی می‌کنید. دلیل این حس سنگینی این است که دیگر نیروی شناوری در آب وجود ندارد. این نیروی شناوری از کجا می‌آید؟ چرا بعضی اجسام می‌توانند شناور باشند و برخی دیگر نه؟ آیا به بدن ما هم نیروی شناوری از طرف هوا وارد می‌شود یا فقط بادکنک‌های هلیومی این امتیاز را دارند؟ پاسخ همه این‌ها اصلی به نام «اصل ارشمیدس» (Archimedes’ Principle) است که در این مطلب به آن می‌پردازیم.

پاسخ پرسش‌های بالا و بسیاری پرسش‌های دیگر در این حقیقت نهفته است که فشار با افزایش عمق در سیال زیاد می‌شود. به این معنی که نیروی رو به بالا که به پایین جسم در سیال وارد می‌شود، از نیروی رو به پایینی که به سطح بالای جسم وارد می‌شود بیشتر است. نیروی خالص شناوری، نیرویی است رو به بالا در تمام سیالات که برای تمام اجسام داخل آن‌ها وجود دارد. اگر نیروی شناوری از وزن جسم بیشتر باشد، جسم به سمت بالا حرکت کرده و شناور می‌شود، اما اگر نیروی شناوری از نیروی وزن جسم کمتر باشد، جسم سقوط می‌کند یا در واقع غرق می‌شود. اگر این دو نیرو برابر باشند، جسم در همان عمق معلق خواهد ماند. در تمام این حالات نیروی شناوری وجود دارد.

نیروی شناوری و اصل ارشمیدس

«نیروی شناوری» (Buoyant Force) نیروی خالص رو به بالا در تمام سیالات است که برای تمام اجسام داخل آن‌ها وجود دارد.

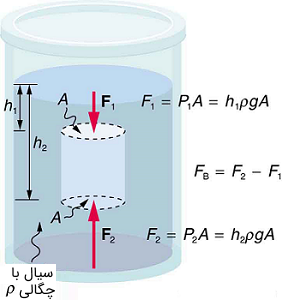$$P = h\rho g$$ با زیاد شدن عمق افزایش می‌یابد. این فشار و نیروی رو به بالا در کف سیلندر از نیروی رو به پایین در بالای آن بیشتر است و اختلاف آن‌ها همان نیرو شناوری $$F_B$$ است." width="282" height="300">

فیلم آموزش فیزیک پایه دهم – فیزیک 1 در فرادرس

کلیک کنید

پرسش بعدی این می‌تواند باشد که اندازه این نیروی شناوری چقدر است؟ برای پاسخ به این پرسش به این فکر کنید که وقتی یک جسم غوطه‌ور را از داخل سیال بر می‌داریم چه اتفاقی می‌افتد؟ مانند شکل زیر.

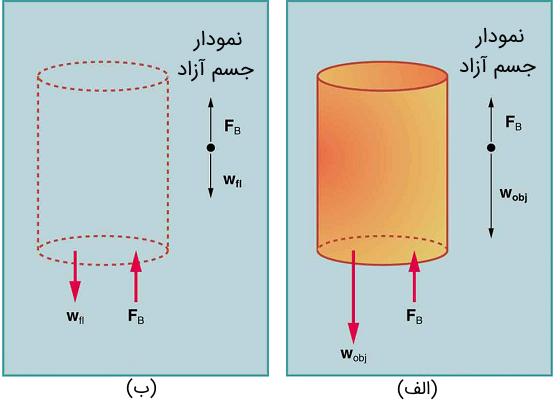$$F_B$$ را تجربه می‌کند. اگر $$F_B$$ از وزن جسم بیشتر باشد، جسم بالا می‌رود. اگر $$F_B$$ کمتر از وزن جسم باشد، جسم غرق می‌شود. (ب) اگر جسم برداشته شود، با سیالی به وزن $$w_{fl}$$ جایگزین می‌شود. از آنجا که این وزن توسط سیال اطراف پشتیبانی می‌شود، نیروی شناوری باید برابر با وزن سیال جابجایی شده باشد. یعنی $$F_B = w_{fl}$$." width="555" height="400">

فضایی که این جسم اشغال کرده بود، با سیالی به وزن $$w_{fl}$$ پر می‌شود. این وزن از طرف سیال اطراف تأمین می‌شود، بنابراین اندازه‌ این نیروی شناوری باید به اندازه نیروی وزن سیال جایگزین شده به جای جسم باشد. این قانون به احترام نبوغ ریاضی‌دان و مخترع یونانی، ارشمیدس (۲۸۷-۲۱۲ پیش از میلاد مسیح)، قانون ارشمیدس نام گرفت. در واقع او سال‌ها پیش از شکل گرفتن مفاهیم مربوط به نیرو به این اصل پی برد. اصل ارشمیدس این‌گونه بیان می‌شود: «نیروی شناوری روی یک جسم برابر است با نیروی وزن سیالی است که به اندازه‌ حجم جسم فضا اشغال می‌کند. به بیان ریاضی:

$$\large F_B = w_{fl}$$

که در آن، $$F_B$$ نیروی شناوری و $$w_{fl}$$ وزن سیال جایگزین شده با جسم است. اصل ارشمیدس یک اصلی کلی است و برای تمام اجسام شناور در هر سیالی صدق می‌کند؛ فرقی نمی‌کند که جسم کاملاً غوطه‌ور باشد و یا بخشی از آن در سیال شناور باشد.

جالب است بدانید که در سال ۲۰۰۸ لباس شنایی با فناوری پیشرفته در مراحل آماده‌سازی المپیک پکن رونمایی شد. یک نگرانی در مورد این لباس (که در واقع برآمده از قونین بین‌المللی هم بود) به همین قانون شناوری برمی‌گشت؛ این لباس نباید از نیروی شناوری به شناگر کمک می‌کرد. فکر می‌کنید چنین چیزی را چطور می‌شد آزمایش کرد؟

چگالی آلومینیوم ۲٫۷ برابر چگالی آب است. یک تکه کوچک فویل آلومینیومی بردارید و آن را با دست مچاله کنید تا شبیه یک توپ کوچک شود. آن را در آب بیندازید. آیا فرو می‌رود؟ چرا؟ آیا می‌توانید آن را غرق کنید (کاری کنید در انتهای ظرف فرورفته باقی بماند)؟

یک تکه گِل یا خمیر بردارید و در آب بیندازید. می‌بینید که غرق می‌شود. اکنون تکه گل خمیری خود را به شکل قایق فرم دهید و روی آب بگذارید، می‌بینید که شناور خواهد شد. قایق به دلیل شکلش، آب جایگزین بیشتری نسبت به گل توپی‌شکل به خود اختصاص می‌دهد و بنابراین نیروی شناوری بیشتری نصیبش می‌شود. به طور مشابه، کشتی‌های فولادی نیز به همین شکل شناوری را تجربه می‌کنند.

مثالی از اصل ارشمیدس

(الف) نیروی شناوری ۱۰۰۰۰ تن فولاد را حساب کنید، به طوری که کاملاً در آب غوطه‌ور باشد و سپس این نیرو را با وزن فولاد مقایسه کنید.

فیلم آموزش فیزیک پایه 3 – جامع و کاربردی در فرادرس

کلیک کنید

(ب) در حالتی که فولاد به شکل قایق درآمده باشد و بتواند صدهزار مترمکعب آب را جایگزین کند، بیشیه‌ نیروی شناوری که آب می‌تواند به این فولاد وارد کند چقدر است؟

حل (الف): برای پیدا کردن نیروی شناوری باید وزن آب جایگزین را بیابیم. این کار را با استفاده از چگالی آب و فولاد انجام می‌دهیم. باید توجه داشته باشیم از آنجا که فولاد به طور کامل شناور شده است، تمام حجم فولاد با حجم آب جایگزین برابر است. بنابراین وقتی که حجم آب را بفهمیم می‌توانیم جرم و وزن آن را نیز حساب کنیم.

ابتدا از تعریف چگالی $$\rho=m/V$$ استفاده می‌کنیم تا حجم فولاد را به دست آوریم و سپس مقادیر جرم و چگالی را جایگزین می‌کنیم.

$$\large V _ { s t } = \dfrac { m _ { s t } } { \rho _ { s t } } = \dfrac { 1.00 \times 1 0 ^ 7 \, k g } { 7.8 \times 1 0 ^ 3 \, k g / m ^ 3 } = 1.2 8 \times 1 0 ^ 3 \, m ^ 3 .$$

از آنجا که فولاد کاملاً در آب غوطه‌ور شده است، حجم آب جایگزین ($$V_W$$) با حجم به دست آمده در بالا یکی است. اکنون می توانیم جرم آب جابجا شده را با رابطه‌ زیر به دست آوریم:

$$\large \begin {align*} m _ W & = \rho _W V _ W = ( 1.000 \times 1 0 ^ 3 \, k g / m ^ 3) ( 1.28 \times 1 0 ^ 3 \, m ^ 3 ) \\ & = 1.3 \times 10^6 \, kg. \end {align*}$$

توسط اصل ارشمیدس وزن آب جابجا شده و بنابراین نیروی شناوری به دست می‌آید:

$$\large \begin {align*} F_B &= w_W = m_Wg = (1.28 \times 10^6\space kg)(9.80 \, m/s^2) \\ & = 1.3 \times 10^7 \, N.\end {align*}$$

همچنین وزن فولاد برابر با $$m_W g = 9.80 \times 10^7 \, N$$ است که بسیار بزرگ‌تر از نیروی شناوری است. بنابراین فولاد در حال غوطه‌وری باقی خواهد ماند.

حل (ب): در اینجا بیشینه‌ حجم آب که با قایق جایگزین می‌شود داده شده است. بنابراین نیروی شناوری وزن آبی به این حجم می‌شود. جرم آب جابجا شده از رابطه‌ آن با چگالی و حجم به دست می‌آید:

$$\large \begin {align*} m_W & = \rho_WV_W = (1.000 \times 10^3 \, kg/m^3)(1.00 \times 10^5 \, m^3) \\ &= 9.80 \times 10^8 \, kg.\end {align*}$$

بیشینه‌ نیروی شناوری در واقع نیروی وزن این حجم از آب است:

$$\large \begin {align*} F_B & = w_W = m_W g = (1.00 \times 10^8 \, kg)(9.80 \, m/s^2)\\ &=9.8 \times 10^8 \, N.\end {align*}$$

بنابراین، بیشینه‌ نیروی شناوری ۱۰ برابر وزن فولاد است، به این معنا که این کشتی فولادی می‌تواند تا ۹ برابر وزن خود بارگیری کند و همچنان در آب شناور بماند.

چگالی و اصل ارشمیدس

چگالی نقش کلیدی و مهمی در اصل ارشمیدس دارد. چگالی میانگین یک جسم، چیزی است که مشخص می‌کند آیا جسم شناور می‌شود یا نه. اگر چگالی آن کمتر از چگالی سیال اطرافش باشد شناور می‌ماند. دلیل این مسئله را به آسانی می‌توان این‌طور بیان کرد که سیال جابجا شده به اندازه‌ حجم جسم جرم بیشتری دارد و بنابراین نیروی شناوری که از این طریق به جسم وارد می‌شود، بزرگ‌تر از وزن جسم بوده و باعث شناوری آن می‌شود. با همین استدلال، اگر جسم چگال‌تر از سیال باشد غرق می‌شود.

فیلم آموزش فیزیک 3 – حل تمرین در فرادرس

کلیک کنید

وسعت سطحی که یک جسم در آن غوطه‌ور می‌شود، به این بستگی دارد که که چگالی جسم چگونه با چگالی و سطح سیال مرتبط می‌شود. برای مثال، در شکل زیر کشتی بارگیری شده نسبت به کشتی بدون بار چگالی بیشتری دارد و طبیعتاً بیشتر در آب فرو رفته است. می‌توان یک بیان کمّی برای نشان نسبت شناوری جسم ارائه داد که چگالی را لحاظ می‌کند. نسبت حجم شناور جسم به کل حجم آن، نسبت شناوری گفته می‌شود:

$$\large \dfrac{V_{sub}}{V_{obj}} = \dfrac{V_{fl}}{V_{obj}}.$$

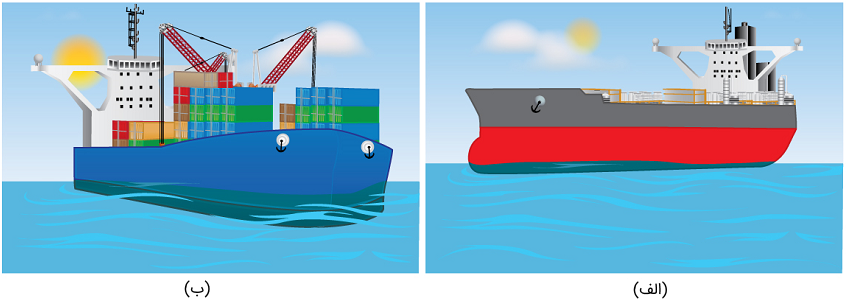
حجم غوطه‌ور جسم دقیقاً با حجم آب جابجا شده که با $$V_{fl}$$ نشان می‌دهیم، برابر است. بنابراین اکنون با جایگزین کردن فرمول چگالی می‌توانیم رابطه بین چگالی‌ها را به دست آوریم:

$$\large \dfrac{V_{fl}}{V_{obj}} = \dfrac{m_{fl}/\rho_{fl}}{m_{obj}/\overline{\rho}_{obj}}$$

که در آن، $$\overline{\rho}_{obj}$$ چگالی متوسط جسم و $$\rho_{fl}$$ چگالی سیال است. از آنجا که جسم غوطه‌ور است، جرم آن و جرم آب جابجا شده یکسان است، پس می‌توان آن‌ها را از معادله حذف کرد و بنابراین نسبت چگالی جسم به سیال به دست می‌آید:

$$\large \dfrac{\overline{\rho}_{obj}}{\rho_{fl}}.$$

مثال‌های زیادی برای شناوری اجسام سبک در سیالات چگال‌تر وجود دارد، مثل شناور ماندن روغن روی آب، یک بادکنک با هوای گرم، یک کوه یخ شناور و... .

یکی از تکنیک‌های مرسوم برای مشخص کردن چگالی در شکل زیر نشان داده شده است. وزن یک جسم (در اینجا، یک سکه) در هوا اندازه گرفته می‌شود و سپس در حالی که در سیال غوطه‌ور است، نیز وزن آن را اندازه می‌گیریم. چگالی سکه از این طریق و به واسطه‌ مشخص بودن چگالی سیال قابل محاسبه است. به همین ترتیب، اگر چگالی سکه مشخص باشد می‌توان چگالی سیال را مشخص کرد. تمام این محسبات بر پایه اصل ارشمیدس هستند.

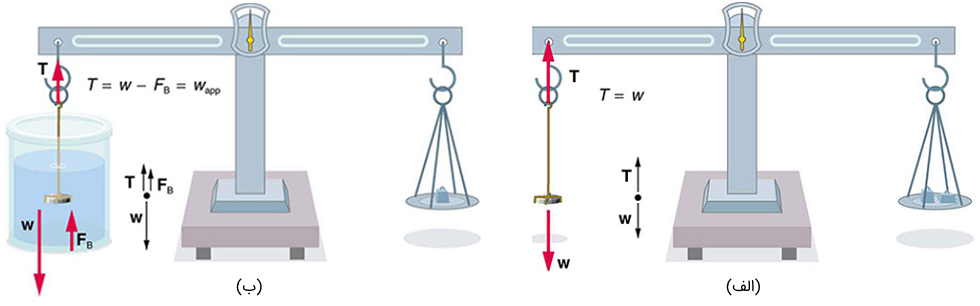
اصل ارشمیدس بیان می‌کند که نیروی شناوری روی جسم با وزن سیال جابجا شده برابر است. این مسئله به این معناست که جسم در حالت شناوری در سیال وزن کمتری دارد، به این وضعیت اصطلاحاً اندازه‌گیری وزن ظاهری جسم می‌گوییم. در واقع، جسم به اندازه‌ وزن سیال جابجا شده دچار کمبود وزن می‌شود.

این مسئله به نوعی داستان کشف اصل ارشمیدس را برایمان بازگو می‌کند. داستان این کشف مهم از این قرار است که پادشاهِ سیراکوز از ارشمیدس می‌خواهد که مشخص کند آیا سازنده‌ تاج پادشاهی تاجی تماماً از طلای خالص برای او ساخته و یا ناخالصی در کار است. تشخیص خلوص طلا از روی رنگ آن کار دشواری است، زیرا ممکن است با فلزات دیگر ترکیب شده باشد اما همچنان به رنگ زرد طلای خالص بدرخشد. علاوه‌ بر این، سایر روش‌های محک زدن خلوص طلا هنوز پیدا نشده بود. با این حال مردمان روزگار باستان هم می‌دانستند که چگالی طلا از هر ماده‌ شناخته شده‌ای در آن زمان بیشتر است. ارشمیدس سخت مشغول تلاش برای وظیفه‌ای بود که پادشاه بر عهده‌اش نهاده بود، تا اینکه یک روز از کمکی که آب در یک حمام عمومی به او عرضه داشت بهره گرفت. او به اصلی که امروز به نامش معروف است رسید و هیجان‌زده و برهنه در خیابان‌های شهر فریاد می‌زد: اورکا! اورکا! که به زبان یونانی یعنی «یافتم!».

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• آموزش فیزیک پایه ۱
• دروس رسمی دبیرستان و پیش‌دانشگاهی
• آموزش جامع فیزیک دبیرستان
• توان در فیزیک — به زبان ساده
• واحدهای اندازه‌گیری الکتریکی — به زبان ساده
• سنسور دما — به زبان ساده

^^