کار مجازی در استاتیک – به زبان ساده

در این مقاله قصد داریم به بررسی مفاهیم اولیه کار مجازی بپردازیم و از آن در حل برخی مسائل مطرح شده در مهندسی مکانیک استفاده کنیم. پیش از آن که وارد بحث اصلی شویم، مقدماتی را در مورد مفهوم کار و تعادل ارائه می‌کنیم تا ابهامات احتمالی در مسیر این آموزش برطرف شود. همان‌طور که می‌دانید کار یک کمیت نرده‌ای است که با $$U$$ نشان داده شده و به طور کلی به صورت حاصل‌ضرب نیرو در جابجایی تعریف می‌شود. برای تعریف دقیق کار، آن را به دو دسته تقسیم می‌کنیم تا بررسی و فرمول‌بندی آن شفاف‌تر انجام شود.

کار انجام شده توسط نیرو

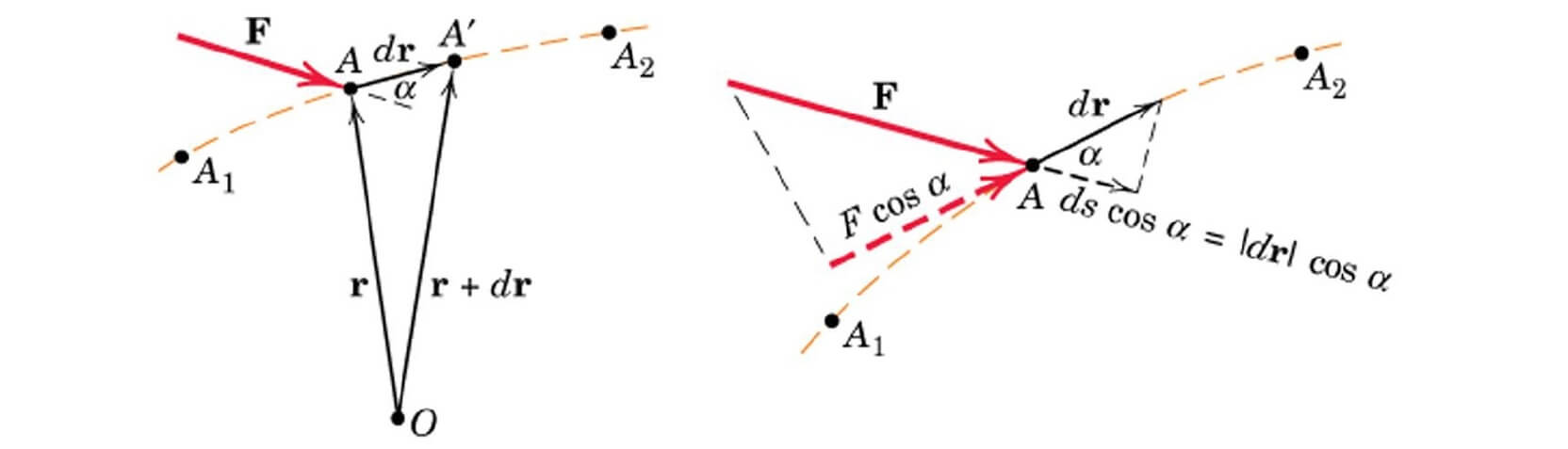
نیروی $$F$$ را در نظر بگیرید که مطابق شکل زیر، ذره را از نقطه $${A_1}$$ تا $${A_2}$$ جابجا می‌کند.

برای شروع محاسبات، جابجایی کوچکی به اندازه $$dr$$ را در نظر می‌گیریم. کار انجام شده توسط نیروی $$F$$ در حین این جایجایی، بازنویسی آن در مختصات سه‌بعدی و بالاخره محاسبه انتگرال از نقطه $${A_1}$$ تا $${A_2}$$ را در ادامه خواهیم دید.

$$dU=F.dr$$

$$dU=F\:ds\:\cos\alpha$$

$$dU=(i\:F_x\:+j\:F_y\:+k\:F_z).(i\:dx\:+j\:dy\:+k\:dz)\\= F_xdx\:+F_ydy\:+F_zdz$$

$$U=\int_{}^{} F.dr=\int_{}^{}(F_x\:dx\:+F_y\:dy\:+F_z\:dz)$$

$$U=\int_{}^{} F\:\cos\alpha\:ds$$

با توجه به رابطه به دست آمده، می‌توان نتیجه گرفت نیروهایی وجود دارند که کار انجام شده توسط آنها صفر است. به عنوان مثال می‌توان به موارد زیر اشاره کرد:

• نیرویی که به نقطه‌ای ثابت وارد می‌شود و جابجایی این نقطه صفر است.
• نیرویی که عمود بر جهت حرکت وارد می‌شود.
• نیروی عکس‌العمل که به یک تکیه‌گاه لولایی وارد می‌شود.
• نیروی عکس‌العمل در یک سطح بدون اصطکاک که جسمی روی آن حرکت می‌کند.
• نیروی وزن در جسمی که مرکز ثقل آن فقط در راستای افقی جابجا می‌شود.
• نیروی اصطکاک روی چرخی که بدون لغزش حرکت می‌کند.

حتی می‌توان از این هم فراتر رفت و به مثال‌هایی رسید که در آنها برآیند کار انجام شده توسط تمام نیروها صفر باشد؛ مانند اجسامی که توسط یک لولای بدون اصطکاک به هم متصل شده‌اند، یا اجسامی که توسط یک طناب کشیده شده، به هم متصل شده‌اند و همچنین نیروهای داخلی که بخش‌های مختلف یک جسم صلب را در کنار هم نگه داشته‌اند.

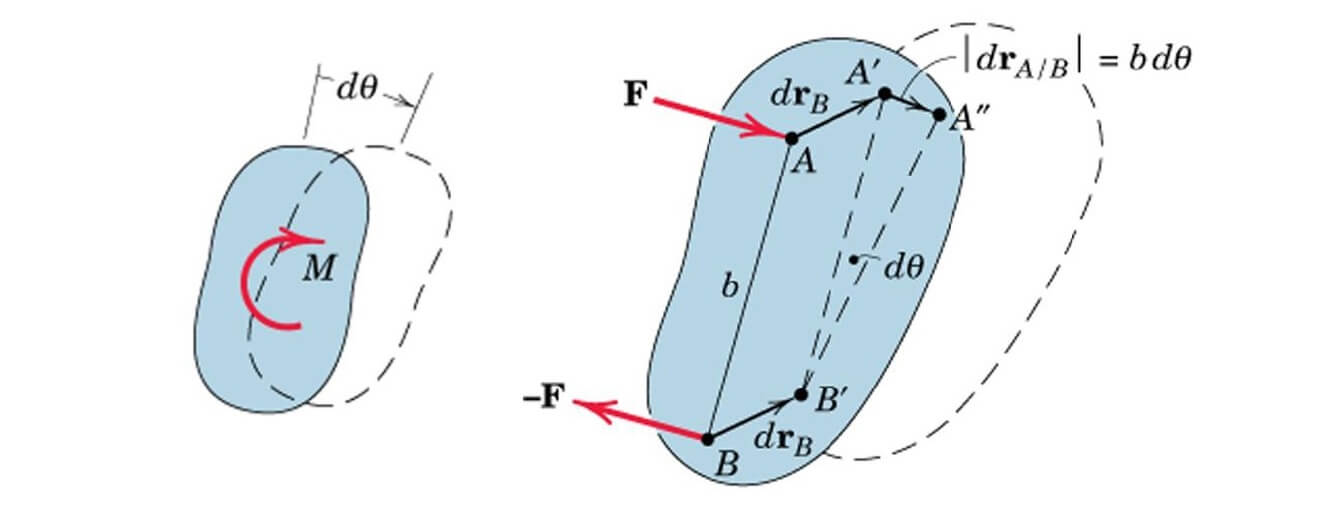
کار انجام شده توسط گشتاور

گشتاور $$M$$ را در نظر بگیرید که مطابق شکل زیر، جسم صلب را از $$AB$$ تا $$A^{\prime\prime}B^{\prime}$$ جابجا می‌کند. این بار محاسبات را به دو بخش تقسیم می‌کنیم. ابتدا جابجایی خطی $$AB$$ به $$A^{\prime}B^{\prime}$$ را در نظر می‌گیریم. در این حالت مطابق آنچه در قسمت قبل توضیح دادیم، کار انجام شده توسط دو نیروی $$F$$ و $$-F$$ یکدیگر را خنثی می‌کنند و مجموع کار انجام شده تا $$A^{\prime}B^{\prime}$$ برابر صفر می‌شود.

حال در بخش دوم این جابجایی، دوران $$A^{\prime}B^{\prime}$$ را حول نقطه $$B^{\prime}$$ در نظر می‌گیریم. در این حالت، کار انجام شده توسط نیروی $$F$$ به شیوه زیر قابل محاسبه خواهد بود. بدین ترتیب مجموع کار انجام شده توسط گشتاور $$M$$ در دوران صفحه‌ای، محاسبه می‌شود. در این حالت نیز اگر گشتاور $$M$$ با زاویه $$\theta$$ هم‌جهت باشد، علامت کار مثبت و در غیر این صورت، علامت کار منفی است.

$$U = F.dr_{A/B} = Fbd\theta$$

$$M = Fb$$

$$dU = Md\theta$$

$$U=\int Md\theta$$

با توجه به رابطه‌ای که برای محاسبه کار تعریف شد، یعنی حاصل‌ضرب نیرو در جابجایی، بُعد به دست آمده برای کمیت کار به صورت زیر است.

$$(J) = N.m$$ ژول

مطابق با این رابطه، کاری که توسط نیروی یک نیوتن در جهت جابجایی یک متر انجام می‌شود، برابر با یک ژول است. به این نکته توجه داشته باشید که بُعد به دست آمده برای کار و گشتاور دقیقاْ یکسان است. در حالی که از نظر فیزیکی هر کدام کمیت کاملاْ متفاوتی هستند. کار یک کمیت نرده‌ای است که با ضرب داخلی نیرو در جابجایی به دست می‌آید. حال آنکه گشتاور یک کمیت برداری است و با ضرب خارجی نیرو در جابجایی محاسبه می‌شود. بدین ترتیب واحد اندازه‌گیری کار، ژول و واحد اندازه‌گیری گشتاور، نیوتن متر است.

مفهوم کار مجازی

تمام توضیحاتی که تا به اینجا ارائه شد، مربوط به اجسامی بود که در حالت تعادل هستند. حال سوال اینجاست که برای اجسامی که از بخش‌های به‌هم پیوسته تشکیل شده‌اند و این بخش‌ها نسبت به هم حرکت دارند، چه باید کرد؟ آیا باز هم می‌توان از این رابطه‌ها استفاده کرد؟ پاسخ این سوال، برخلاف انتظار، مثبت است. یعنی هنوز هم رابطه‌های تعریف شده در قسمت کار، معتبر هستند ولی فقط پیچیدگی مسئله را بیشتر می‌کنند.

زیرا دیگر به جای یک وضعیت تعادل منحصر به فرد، چندین وضعیت تعادل امکان‌پذیر خواهد بود و همین موضوع، موجب طولانی‌تر شدن زمان حل مسئله می‌شود. برای آنالیز سازه‌هایی که دارای اتصال چندگانه هستند و پیکربندی آنها مدام تغییر می‌کند، مفهوم کار مجازی بسیار مناسب است و هنگامی که بتوان رابطه ساده‌ای میان جابجایی نقاطی یافت که نیرو در آنها اعمال شده است، این روش راه‌گشا خواهد بود. روش کار مجازی هم بر پایه مفهوم کار انجام شده توسط یک نیرو استوار است و امکان بررسی پایداری سیستم در نقطه تعادل فرضی را فراهم می‌کند.

کار مجازی براساس جابجایی مجازی تعریف می‌شود. جابجایی مجازی، چیزی نیست که در واقعیت اتفاق بیافتد و فقط فرضیه‌ای است که برای حل مسائل از آن کمک گرفته می‌شود. بدین منظور، موقعیت‌های تعادل مختلفی با یکدیگر مقایسه می‌شوند تا بهترین موقعیت، انتخاب شود. ذره‌ای مطابق شکل زیر در نظر بگیرید که به دلیل وارد شدن نیروهای مختلف، وادار به جابجایی مجازی کوچکی به اندازه δr می‌شود. کار مجازی متناظر، از رابطه زیر قابل محاسبه است.

$$\delta U = \overrightarrow{F_1}.\delta\overrightarrow{r} + \overrightarrow{F_2}.\delta\overrightarrow{r} + \overrightarrow{F_3}.\delta\overrightarrow{r} + \overrightarrow{F_4}.\delta\overrightarrow{r}= (\overrightarrow{F_1} + \overrightarrow{F_2} + \overrightarrow{F_3}+\overrightarrow{F_4}).\delta\overrightarrow{r} = \overrightarrow{F}.\delta\overrightarrow{r}$$

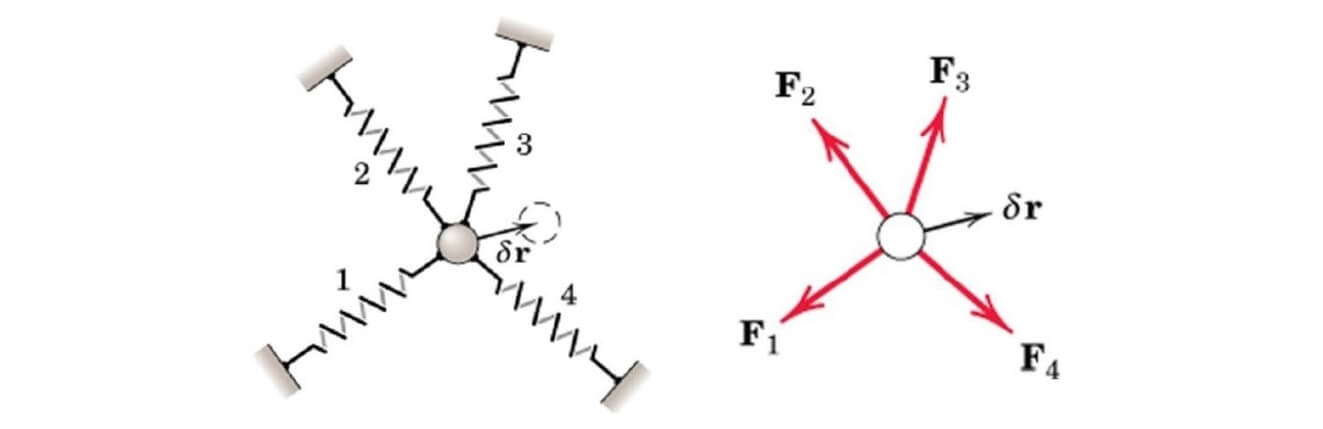
حال اگر بردارهای $$F$$ و δr را برحسب مولفه‌های دستگاه مختصات سه‌بعدی بنویسیم، نتیجه زیر حاصل می‌شود.

$$\delta U=\sum{F}.\delta{r}=(i\sum{F_x}\:+j\sum{F_y}\:+k\sum{F_z}).(i\:\delta x\:+j\:\delta y\:+k\:\delta z)\\=\sum{F_x}\delta x\:+\sum{F_y}\delta y\:+\sum{F_z}\delta z=0$$

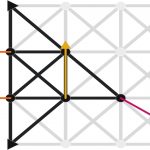
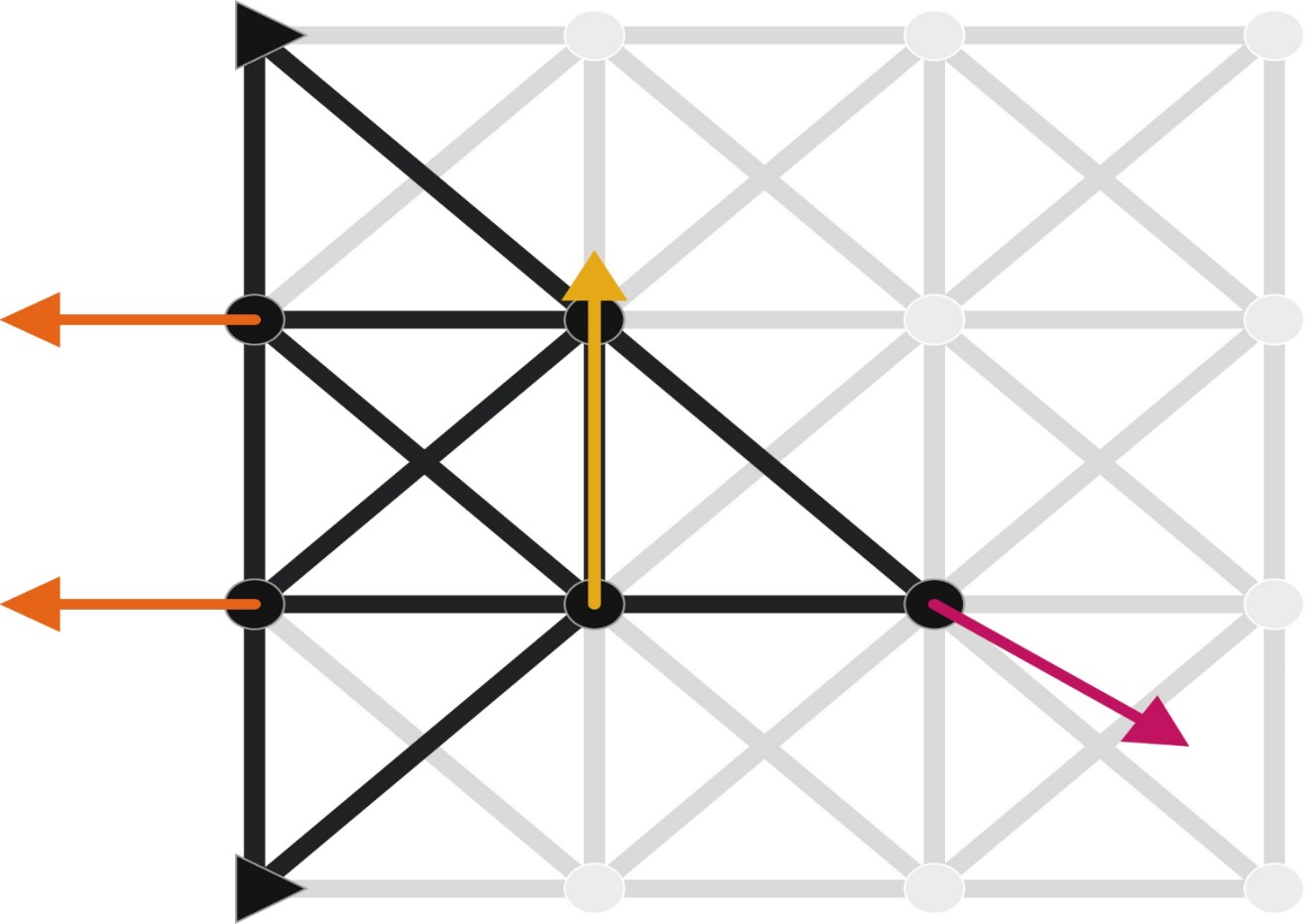
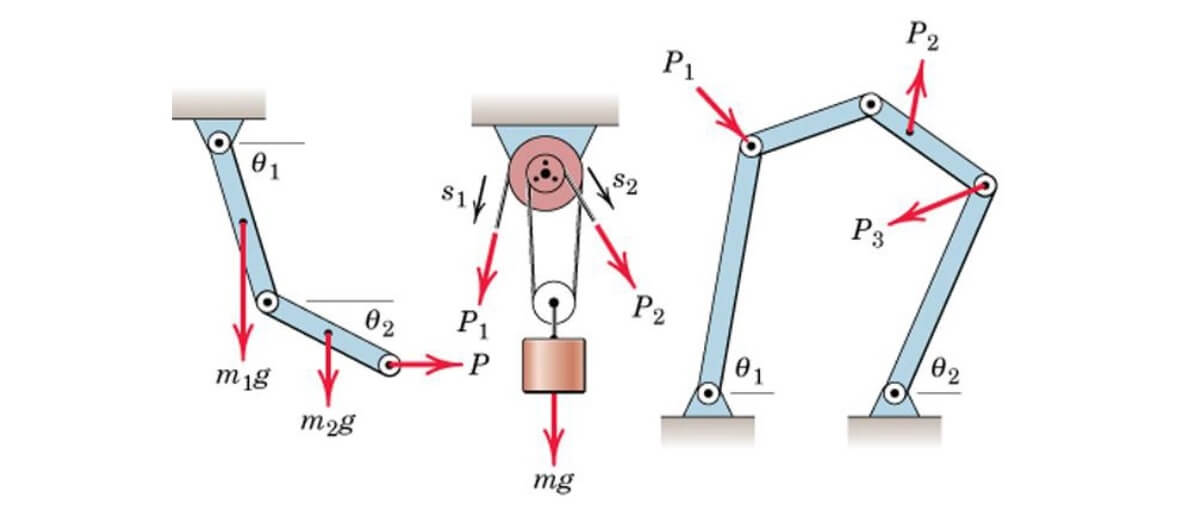
از آنجایی که برآیند نیروی $$F$$ در هر سه جهت مختصاتی صفر است، نتیجه عبارت بالا نیز برابر صفر می‌شود. به عبارت دیگر، تعادل ذره را می‌توان به صورت $$\delta{U}=0$$ نشان داد. این شرط، یعنی صفر بودن مقدار کار مجازی، برای حالت تعادل، لازم و کافی است و می‌تواند در هریک از سه جهت دستگاه مختصاتی مورد استفاده قرار بگیرد. با توجه به این موضوع، در ارتباط با مفهوم کار مجازی، می‌توان چند نتیجه مهم گرفت. اول اینکه اگر ذره‌ای در حالت تعادل باشد، مجموع کار مجازی ناشی از نیروهای وارد بر ذره، برای هرگونه جابجایی مجازی، صفر است. حال اگر جسم صلبی در حالت تعادل باشد، مجموع کار مجازی ناشی از نیروهای خارجی وارد بر ذره، برای هرگونه جابجایی مجازی، صفر است. بنابراین اگر مجموعه‌ای از اجسام صلب متصل به هم، در حین جابجایی مجازی همچنان متصل بماند، فقط کار ناشی از نیروهای خارجی باید در نظر گرفته شود. زیرا نیروهای داخلی، کار یکدیگر را خنثی می‌کنند. به شکل زیر توجه کنید.

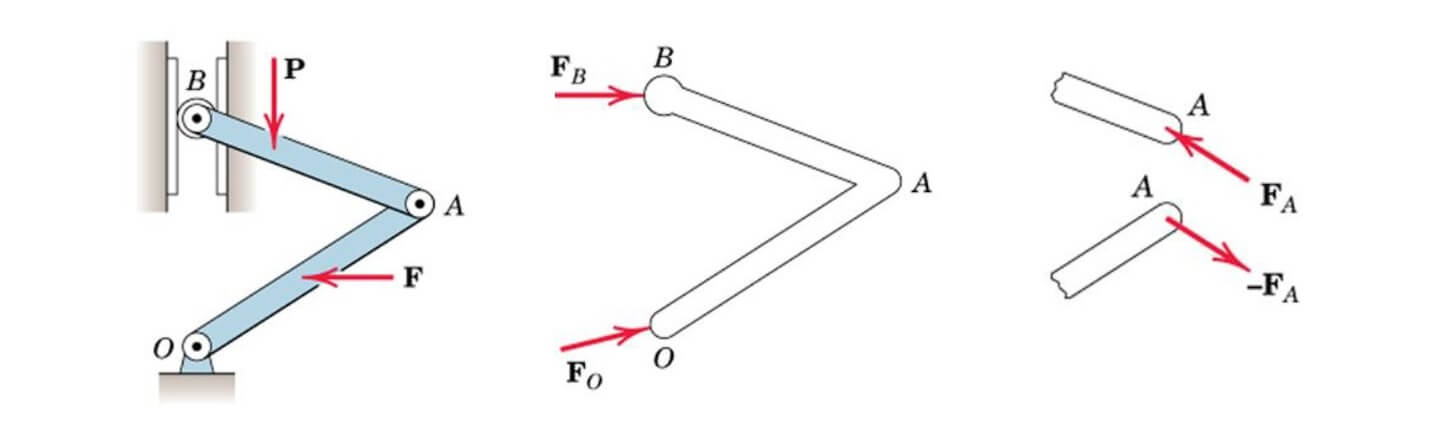
در تصویر سمت چپ، نیروهای $$P$$ و $$F$$، به عنوان نیروهای خارجی به سیستم وارد شده‌اند و کار مجازی آنها غیر صفر است. در مورد دو تصویر دیگر، تمام نیروهای نشان داده شده، از جنس نیروهای داخلی هستند و دو به دو کار یکدیگر را خنثی خواهند کرد. حال برای درک بهتر موضوعاتی که تا به اینجا مطرح شد، به دو مثالی که در ادامه می‌آید توجه کنید.

مثال ۱

در شکل زیر، نیروی خارجی $$P$$ به جسم وارد می‌شود. وزن جسم قابل صرف نظر کردن است و می‌خواهیم مفهوم کار مجازی را برای این وضعیت بنویسیم. همان‌طور که گفتیم، از آنجایی که کار مجازی انجام شده روی هریک از ذرات تشکیل دهنده یک جسم صلب، صفر است، مجموع کار مجازی انجام شده روی جسم صلب نیز صفر خواهد بود. در این شکل، کار انجام شده توسط نیروی $$P$$، برابر با $$-Pa\:\delta\theta$$ و کار انجام شده توسط نیروی $$R$$ برابر با $$+Ra\:\delta\theta$$ است.

با توجه به مفهوم کار مجازی یا همان شرط $$\delta U = 0$$ عبارت زیر به دست می‌آید. (توجه کنید که چون در این مثال فقط از یک جسم صلب منفرد استفاده شده است، مفهوم کار مجازی کمک خاصی نمی‌کند.)

$$-Pa\:\delta\theta\:+Rb\:\delta\theta\:=0$$

$$Pa-Rb=0$$

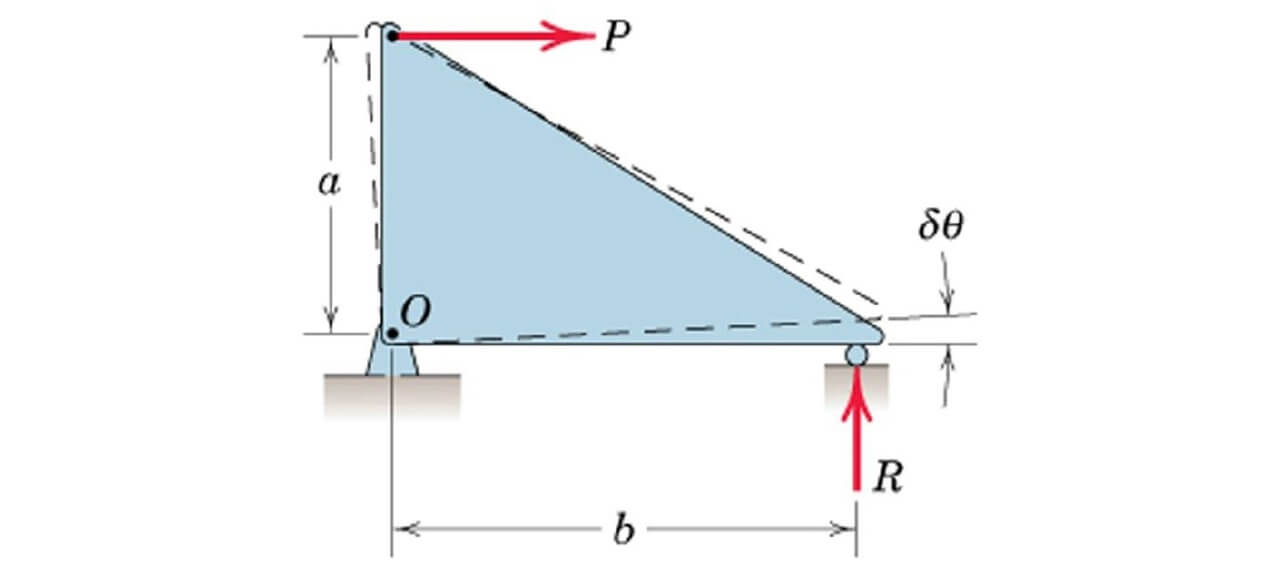
مثال ۲

در مثال دوم از دو جسم صلب متصل به هم استفاده شده است. مطابق شکل زیر نیروی $$P$$ به نقطه‌ $$V$$ وارد می‌شود. با صرف‌نظر از هرگونه اصطکاک، می‌خواهیم نیروی عکس‌العمل $$Q$$ را به دست آوریم. کار انجام شده توسط نیروهای خارجی برای یک دوران مجازی به اندازه $$\delta\theta$$ را در نظر بگیرید. با توجه به گفته‌های قبلی، می‌دانیم فقط کار انجام شده توسط نیروهای $$P$$ و $$Q$$ مخالف صفر است. با توجه به شکل، مشخص است که افزایش X_B، موجب کاهش مقدار Y_C می‌شود. با نوشتن معادله دیفرانسیلی برای کار، عبارت زیر به دست می‌آید.

در ادامه، پارامترهای Y_C ،X_B و مقادیر دیفرانسیلی آنها را بازنویسی می‌کنیم تا نتیجه نهایی به دست بیاید.

$$\delta U=\delta{U_Q}+\delta{U_P}=-Q\:\delta{x_B}-P\:\delta{y_C}=0$$

$$x_B=2l\:\sin\theta\:\:\Rightarrow\:\:x_B=2l\:\cos\theta\:\delta\theta \\~\\y_C=l\:\cos\theta \:\:\Rightarrow\:\: y_C=-l\:\sin\theta\:\delta\theta$$

$$-2Ql\:cos\theta\:\delta\theta+Pl\:sin\theta\:\delta\theta=0$$

$$\Rightarrow\:Q=\frac{1}{2}\:P\:tan\theta$$

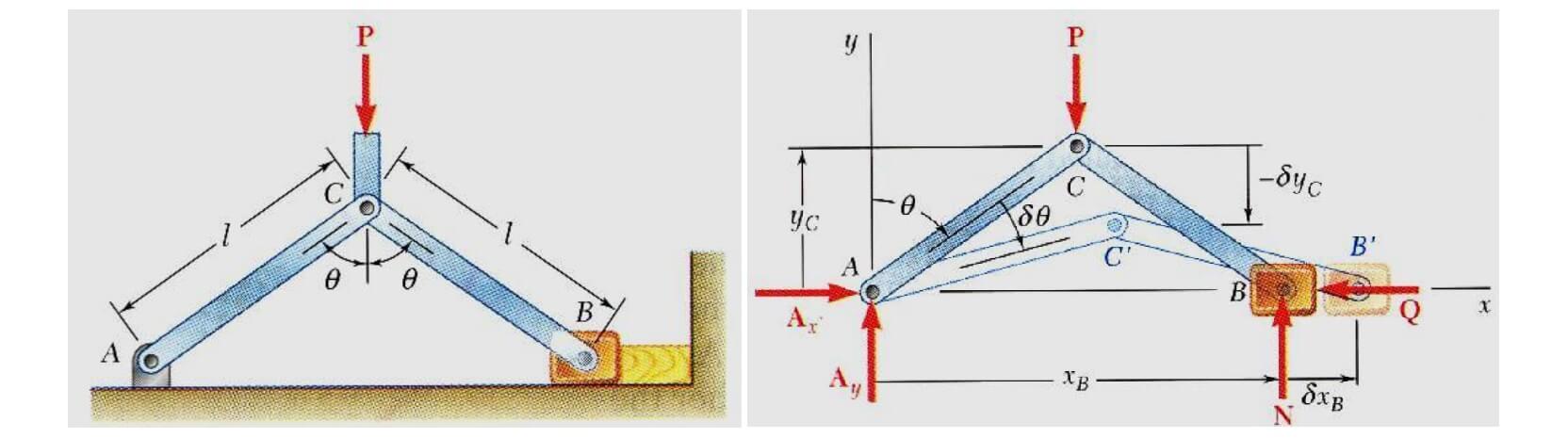
در مثال‌هایی از این دست، به دلیل قیودی که در تکیه‌گاه‌ها وجود دارد، جابجایی فقط در مسیرهایی محدود انجام می‌شود. در نتیجه می‌توان فقط بارهای خارجی و نیروهای اصطکاک را در نظر گرفت.

تا اینجا، تا حدودی با مفهوم کار مجازی آشنا شدیم. با این روش می‌توان موقعیت تعادل را برای سیستمی که تحت بارهای مشخصی قرار گرفته، تعیین کرد. یکی از مزیت‌های استفاده از این روش این است که برای مشخص کردن ارتباط بین نیروهای وارد شده، نیازی به جدا کردن قسمت‌های مختلف سیستم از یکدیگر نیست. همچنین می‌توان بدون در نظر گرفتن نیروهای عکس‌العمل، ارتباط بین نیروها را به دست آورد. ضمناْ باید به این موضوع توجه کرد که در این روش، کار ناشی از نیروهای اصطکاک داخلی در حین هر جابجایی مجازی، باید قابل چشم‌پوشی باشد. در غیر این صورت و در شرایطی که اصطکاک داخلی قابل ملاحظه باشد، کار انجام شده توسط نیروهای داخلی نیز باید در محاسبات وارد شود. در ادامه، مفاهیم درجه آزادی، اصطکاک و راندمان مکانیکی را یادآوری می‌کنیم تا برای حل دو مثال پایان‌بخش این مقاله آماده شویم.

درجه آزادی

درجه آزادی عبارت است از تعداد مختصات مستقلی که برای توصیف یک سیستم مورد نیاز است.

به شکل‌های زیر توجه کنید. برای تعیین موقعیت هریک از اجزای سیستم الف، تنها یکی از مختصات جابجایی یا دوران کافی است. ولی برای سیستم‌هایی با دو درجه آزادی (مانند شکل ب)، تعداد مختصات مستقل از هم باید دو باشد.

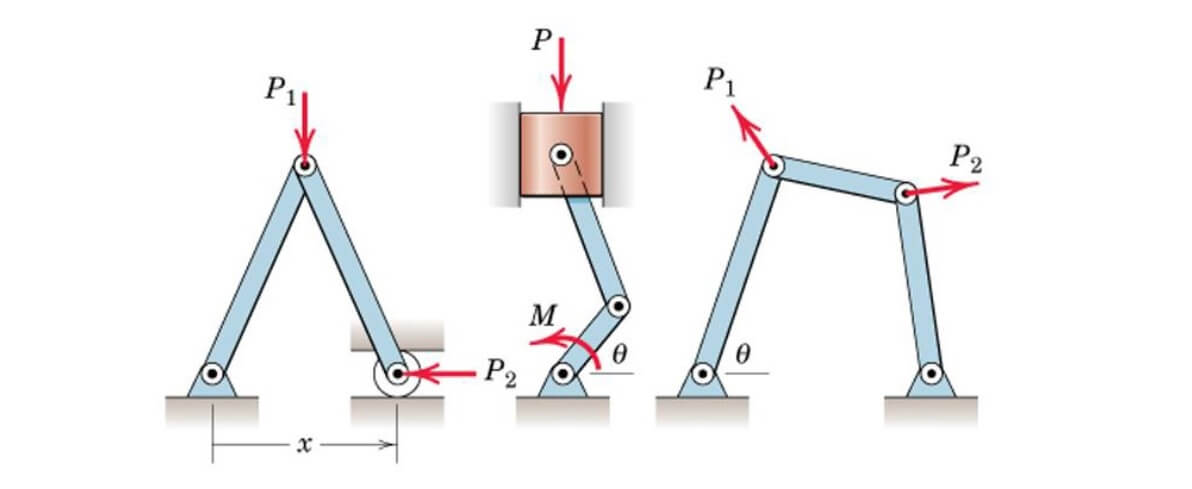
سیستم‌های دارای اصطکاک

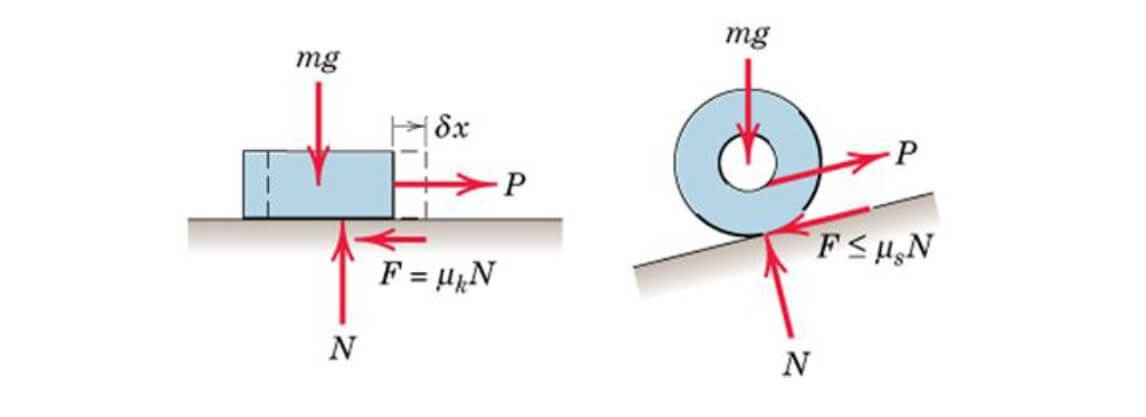
تا به اینجا، مفهوم کار مجازی را فقط برای سیستم‌های ایده‌آل بررسی کردیم. اگر اصطکاک سیستم، قابل چشم‌پوشی نباشد (سیستم‌های واقعی)، کار انجام شده توسط نیروهای خارجی، به وسیله کار انجام شده توسط نیروهای اصطکاک، خنثی می‌شود. در حین جابجایی مجازی به اندازه δx، کار انجام شده توسط نیروی اصطکاک جنبشی با رابطه $$-\mu_kN\delta x$$ محاسبه می‌شود. در حین چرخیدن چرخ، تا زمانی که لغزش اتفاق نیافتد، نیروی اصطکاک استاتیکی کار انجام نمی‌دهد.

راندمان مکانیکی

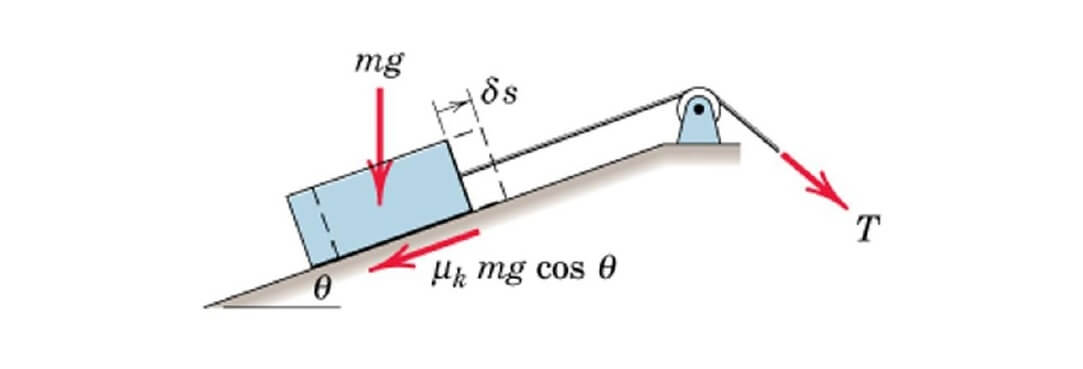
کار خروجی یک دستگاه همیشه از کار ورودی آن کمتر است؛ زیرا همواره مقداری انرژی به دلیل اصطکاک هدر می‌رود. راندمان مکانیکی به صورت نسبت کار خروجی به کار ورودی محاسبه و با حرف e نشان داده می‌شود. در مکانیزم‌های ساده با یک درجه آزادی که به طور یکنواخت کار می‌کنند، راندمان مکانیکی را می‌توان به کمک مفهوم کار مجازی بیان کرد.

با توجه به شکل پایین، برای جابجایی مجازی به اندازه δs، کار خروجی باید به میزان $$mg\:\delta s\:\sin\theta$$ باشد تا بتواند جعبه را به سمت بالا حرکت دهد. از طرفی، کار ورودی نیز با عبارت $$T\:\delta s=mg\:\sin\theta\:\delta s+\mu_k\:mg\:\cos\theta\:\delta s$$ محاسبه می‌شود. در نتیجه، راندمان مکانیکی به صورت زیر، محاسبه می‌شود. همان‌طور که مشخص است، هرچه اصطکاک کمتر باشد، راندمان به عدد یک نزدیک‌تر می‌شود.

$$e=\frac{mg\:\delta s\:\sin\theta}{mg(\sin\theta+\mu_k\:\cos\theta)\:\delta s}=\frac{1}{1+\mu_k\:\cot\theta}$$

مثال ۳

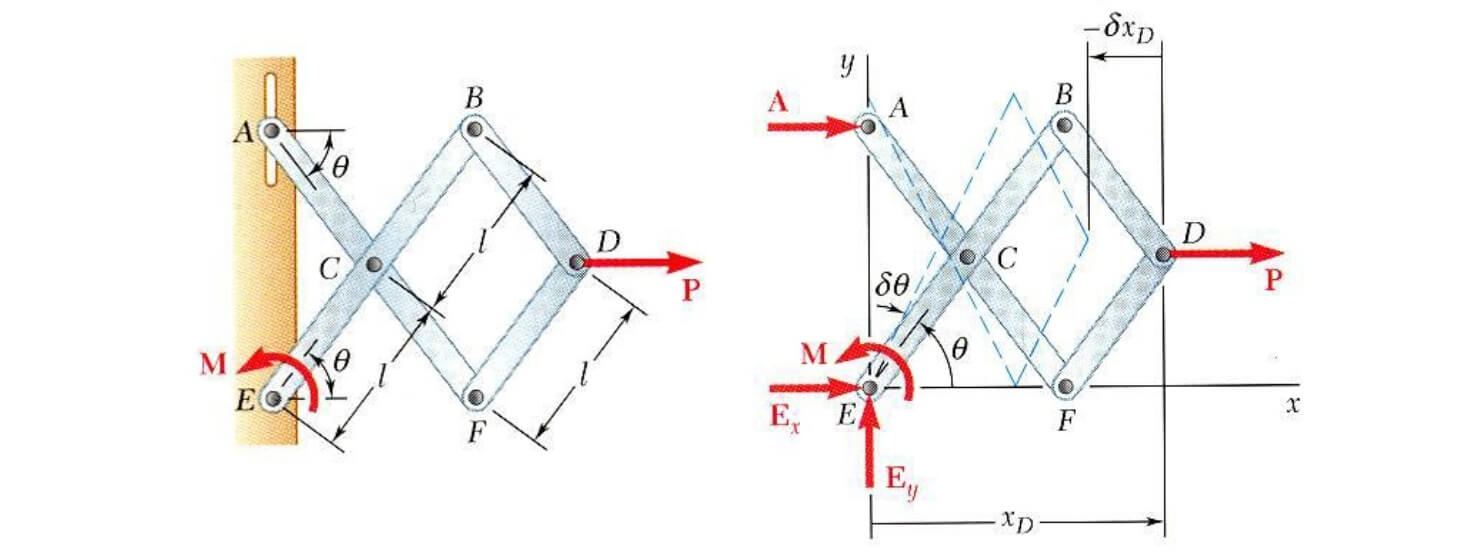
در این مثال می‌خواهیم مقدار گشتاور $$M$$ را طوری به دست آوریم که تعادل سیستم حفظ شود. بدین منظور در نقطه $$E$$، مقدار زاویه $$\theta$$ را به صورت مجازی افزایش می‌دهیم. سپس مفهوم کار مجازی را برای این سیستم می‌نویسیم.

$$\delta U=0=\delta U_M+\delta U_P$$

$$M\:\delta\theta\:+P\:\delta x_D=0$$

حال با بازنویسی پارامترهای $$x_D$$ و $$\delta x_D$$ معادله به صورت زیر و به راحتی حل خواهد شد.

$$x_D=3l\:cos\theta$$

$$\delta x_D=-3l\:sin\theta\:\delta\theta$$

$$M\:\delta\theta\:+P(-3l\:\sin\theta\:\delta\theta)=0$$

$$\Rightarrow\:M=3Pl\:\sin\theta$$

مثال ۴

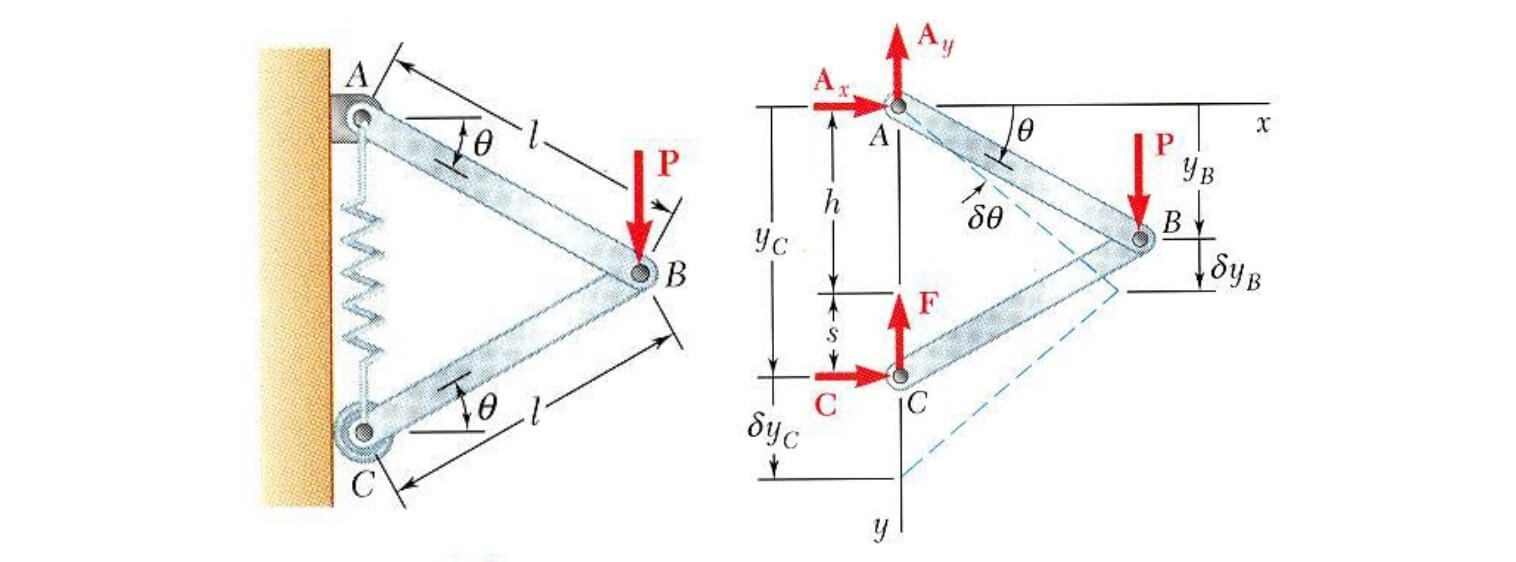
در این مثال، طول اولیه فنر برابر با $$h$$ و ثابت فنر نیز برابر با $$k$$ است. با صرف‌نظر از وزن مکانیزم، می‌خواهیم مقدار زاویه θ را در حالت تعادل به دست آوریم. برای این منظور، مقدار زاویه θ را در نقطه $$A$$ و در جهت مثبت افزایش می‌دهیم. همچنین می‌دانیم نیروی کشش فنر با استفاده از رابطه $$F=ks$$ به دست می‌آید. بنابراین مفهوم کار مجازی را به صورت زیر برای این مکانیزم می‌نویسیم.

$$\delta U=\delta U_B+\delta U_F=0$$

$$\:\:0=P\:\delta y_B+F\:\delta y_C$$
معادله ۱

حال با بازنویسی پارامترهای $$y_B$$ و $$y_C$$ و مشتق‌گیری از آنها، معادله به صورت زیر و به راحتی حل خواهد شد.

$$\:\:y_B=l\:\sin\theta\:\:\Rightarrow\:\:\delta y_B=l\:\cos\theta\:\delta\theta\\‍\\y_C=2l\:\sin\theta\:\:\Rightarrow\:\:\delta y_C=2l\:\cos\theta\:\delta\theta$$
معادله ۲

در نهایت با توجه به معادله ۱ و ۲، نتیجه زیر حاصل می‌شود.

$$\:\Rightarrow\:P(l\:\cos\theta\:\delta\theta)-k(2l\:\sin\theta-h)(2l\:\cos\theta\:\delta\theta)=0$$

$$\Rightarrow\:\:\sin\theta=\frac{P+2kh}{4kl}$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه نرم‌افزارهای مهندسی مکانیک
• خرپا چیست؟ — به زبان ساده
• استاتیک — از صفر تا صد
• تعیین عکس العمل‌های تکیه‌گاهی تیرها — مثال‌های کاربردی

^^