منحنی ROC و کاربردهای آن — به زبان ساده

۱۴۰۶۰ بازدید

آخرین به‌روزرسانی: ۲۷ خرداد ۱۴۰۲

زمان مطالعه: ۱۲ دقیقه

دانلود PDF مقاله

یکی از روش‌های بررسی و ارزیابی عملکرد دسته‌بندی دو دویی، «نمودار مشخصه عملکرد» (Receiver Operating Characteristic) یا به اختصار منحنی ROC است. کارایی الگوریتم‌های «دسته‌بندهای دو دویی» (‌Binary Classifier) معمولا به وسیله شاخص‌هایی مثل «حساسیت» (Sensitivity) و «صراحت» (Specificity) سنجیده می‌شوند. اما در نمودار ROC هر دوی این شاخص‌ها ترکیب شده و به صورت یک منحنی نمایش داده می‌شوند. اغلب برای بررسی کارایی الگوریتم‌های دسته‌بندی یا ایجاد داده‌های رسته‌ای از منحنی ROC استفاده می‌کنند. این موضوع در شاخه یادگیری ماشین با نظارت (Supervised Machine Learning)، بیشتر مورد توجه قرار گرفته است. به همین دلیل این نوشتار از مجله فرادرس را به بررسی منحنی ROC و کاربردهای آن اختصاص داده‌ایم. ابتدا تاریخچه‌ای از پدید آمدن منحنی ROC خواهیم گفت و در ادامه، این منحنی را معرفی و نحوه ترسیم آن را بیان خواهیم کرد. همینطور در این متن، به شاخص‌های مرتبط با منحنی ROC نیز می‌پردازیم.

فهرست مطالب این نوشته

منحنی ROC و کاربردهای آن

منحنی ROC و کاربردهای آن در فراتر از دسته‌بندی دو دویی

خلاصه و جمع‌بندی

به منظور آشنایی بیشتر با روش‌های ارزیابی دسته‌بندها، نوشتارهای دیگر مجله فرادرس مانند روش‌ های ارزیابی نتایج خوشه‌ بندی (Clustering Performance) — معیارهای بیرونی (External Index) و ماتریس درهم ریختگی (Confusion Matrix) — از صفر تا صد را مطالعه کنید. همچنین خواندن مطالب روش های متن کاوی — راهنمای کاربردی و دسته‌ بند بیز ساده (Naive Bayes Classifiers) — مفاهیم اولیه و کاربردها نیز خالی از لطف نیست.

منحنی ROC و کاربردهای آن

شاید بتوان تحلیل سیگنال‌های رادار در جنگ جهانی دوم را اولین زمان ظهور منحنی ROC و کاربردهای آن دانست. البته بعدها از چنین منحنی در «نظریه شناسایی سیگنال» (Signal Detection Theory) نیز استفاده شد. پس از جنگ در «پرل هاربر» (Pearl Harber) در سال ۱۹۴۱، که نیروهایی آمریکایی به شدت آسیب دیدند، ارتش آمریکا تصمیم گرفت سیگنال‌های راداری (Radar Signal) به منظور کشف و شناسایی هواپیماهای ژاپنی را بهبود دهد. برای این کار، آن‌ها توانایی یک گیرنده رادار را در تشخیص هواپیما اندازه‌گیری کردند و از آن پس واژه «مشخصه عملکرد گیرنده» (Receiver Operating Characteristic) برای ارزیابی عملکرد دستگاه‌های تشخیص سیگنال، مورد استفاده قرار گرفت.

فیلم آموزش تحلیل رگرسیون لجستیک دو حالتی در SPSS اس پی اس اس در فرادرس

کلیک کنید

در دهه 1950، منحنی‌های ROC در روانشناسی نیز به کار گرفته شدند تا ضعف در قوه تشخیص انسان‌ها (و گاهی حیوان) را مورد بررسی و ارزیابی قرار دهند. در پزشکی، تجزیه و تحلیل ROC به طور گسترده‌ای در سنجش صحت آزمایش‌های تشخیص پزشکی و تعیین میزان دقت چنین آزمایشاتی، مورد استفاده قرار گرفته است.

منحنی‌های ROC همچنین در اپیدمیولوژی و تحقیقات پزشکی بسیار مورد استفاده قرار می‌گیرند. در رادیولوژی، تجزیه و تحلیل ROC یک روش معمول برای ارزیابی تکنیک‌های جدید رادیولوژی است. همچنین در علوم اجتماعی، آنالیز منحنی ROC اغلب به عنوان «نسبت دقت مشخصه عملکرد» (ROC Accuracy Ratio)، یاد شده و یک تکنیک معمول برای قضاوت در مورد مدل‌های احتمال پیش‌بین (Predictive Probability Model) است.

منحنی ROC و کاربردهای آن در یادگیری ماشین بخصوص در شاخه نظارت شده آن، مفید بوده است. به این ترتیب مقادیر مربوط به منحنی ROC می‌تواند مبنایی برای مقایسه و ارزیابی الگوریتم‌های دسته‌بندی (Classifiers Algorithms) باشد. منحنی‌های ROC همچنین در تأیید پیش بینی‌ها در هواشناسی نیز مورد بهره‌برداری قرار می‌گیرد.

منحنی مشخصه عملکرد چیست؟

یک منحنی مشخصه عملکرد که به اختصار آن را منحنی ROC می‌نامیم، یک نمودار برای نمایش توانایی ارزیابی یک سیستم دسته‌بندی باینری محسوب می‌شود که آستانه تشخیص آن نیز متغیر است.

منحنی ROC توسط ترسیم نسبت یا «نرخ مثبت صحیح» (True Positive Rate) که به اختصار TPR نامیده می‌شود برحسب «نرخ مثبت کاذب» (False Positive Rate) با نام اختصاری FPR، ایجاد می‌شود. البته توجه داشته باشید که آستانه برای این مقادیر، متغیر است. به همین دلیل، یک نمودار پیوسته ایجاد خواهد شد.

Roc curves — منحنی مشخصه عملکرد برای سه روش مختلف دسته‌بندی

«نرخ مثبت صحیح» را در «یادگیری ماشین» (Machine Learning) گاهی «حساسیت» (Sensitivity) یا «بازیابی» (Recall) یا «احتمال شناسایی» (Probability Detection) می‌نامند. همچنین «نرخ مثبت کاذب» هم به صورت «احتمال دریافت اخطار کاذب» (Probability False Alarm) شناخته شده و براساس متمم «ویژگی» (Specificity) سنجیده می‌شود. البته در ادامه هر یک از این نسبت‌ها، در جدول ۱، توصیف خواهند شد.

نکته: با توجه به آزمون فرض آماری و مفاهیم مربوط به آن، منحنی ROC را می‌توان به معنی «توان آزمون» (Test Power) برحسب مقادیر مختلف «خطای نوع اول» (Error I Type) در نظر گرفت که براساس یک نمونه تصادفی تولید شده است.

اگر با زبان شناسایی سیگنال و مخابرات به ROC توجه کنیم، به طور کلی با شرط مشخص بودن توزیع احتمالی برای هر دو بخش (TPR) و (FPR) منحنی ROC در صورتی حاصل خواهد شد، که «تابع توزیع تجمعی» (Cumulative Distribution function) یا سطح زیر منحنی توزیع احتمال تشخیص درست سیگنال را در محور عمودی و تابع توزیع تجمعی تشخیص نادرست سیگنال را در محور افقی در نظر بگیریم.

منحنی ROC را به عنوان «نمودار مشخصه نسبی عملکرد» (Relative Operating Characteristic) نیز می‌شناسند زیرا مقایسه‌ای بین دو نحوه عملکرد (TPR , FPR) ارائه می‌کند. به این ترتیب آنچه امروزه (بدون در نظر گرفتن مفهوم شناسایی سیگنال توسط دستگاه دریافت کننده یا Receiver) به عنوان منحنی ROC می‌شناسیم همان نمودار مشخصه نسبی عملکرد است.

مفاهیم اولیه در منحنی ROC

یک مدل دسته‌بندی، یک نگاشت از مشاهدات به دسته یا گروه‌های مشخص است. از آنجایی که دسته‌بندها (Classifiers) مقادیر حقیقی و پیوسته را تولید می‌کنند، لازم است برحسب یک مقدار آستانه، دسته یا گروه‌ها را مشخص و از یکدیگر مجزا کنیم. برای مثال با توجه به میزان فشار خون فرد (که مقداری پیوسته است) باید افراد را در یکی از دسته‌های بیمار فشار خون یا بدون بیماری، قرار دهیم. به این ترتیب نگاشت از مجموعه اعداد حقیقی به زیر مجموعه‌ای متناهی از اعداد طبیعی، صورت می‌گیرد.

یک مسئله «دسته‌بندی دو دویی» (Binary Classification) را در نظر بگیرید. نتایج این دسته‌بندی با دو برچسب مثبت (P) و منفی (N) مشخص می‌شوند. درست مانند یک آزمایش پزشکی که دارای نتیجه مثبت (بیمار بودن طبق آزمایش) و منفی (نداشتن بیماری طبق آزمایش) است. از این آزمایش پزشکی می‌توان چهار حالت مختلف را در نظر گرفت.

فرض کنید نتیجه براساس پیش‌بینی (آزمایش پزشکی) مثبت (P) است. به این ترتیب:
- اگر نتیجه واقعی نیز مثبت (P) است، این نتیجه را «مثبت صحیح» (TP) می‌نامیم.
- اگر نتیجه واقعی منفی (N) باشد، این نتیجه را به نام «مثبت کاذب» (FP) می‌شناسیم.
فرض کنید نتیجه براساس پیش‌بینی (آزمایش پزشکی) منفی (N) است. در این حالت:
- اگر نتیجه واقعی نیز منفی بوده، چنین وضعیتی را به نام «منفی صحیح» (TN) به کار خواهیم برد.
- ولی اگر نتیجه واقعی مثبت باشد، چنین حالتی به نام «منفی کاذب» (FN) شناخته می‌شود.

حال P را تعداد افرادی در نظر بگیرید که در واقعیت در گروه مثبت قرار دارند. همچنین N نیز بیانگر تعداد افرادی است که در گروه N عضویت دارند. همچنین F و T را هم به صورت اعداد صحیح در نظر داشته باشید که تعداد مشاهدات در هر گروه براساس پیش‌بینی را مشخص می‌کنند. این چهار وضعیت را مطابق با یک جدول توافقی با دو سطر و دو ستون یا یک ماتریس دو در دو، نمایش می‌دهیم. توجه داشته باشید که در اینجا TP, TN, NP, FN تعداد مشاهداتی هستند که در هر یک از این چهار گروه قرار می‌گیرند.

جدول ۱: جدول توافقی برای مقایسه تعداد اعضای در گروه‌های مختلف براساس دسته‌بندی دو دویی

واقعیت

پیش‌بینی

در این صورت گزاره‌های زیر را برای این جدول می‌توان به کار برد:

مثبت صحیح (TP) بیانگر ضربه (hit) یا شناسایی صحیح سیگنال است.
منفی صحیح (TN) به معنی رد صحیح (Correct Reject) سیگنال رسیده است. یعنی تشخیص صحیح یک نویز که ممکن بود به اشتباه سیگنال تلقی شود.
مثبت کاذب (FP) همان اخطار کاذب (False Alarm) است، که می‌توان در آزمون فرض آماری آن را معادل خطای نوع اول (Type I Error) در نظر گرفت. در این حالت یک نویز به عنوان سیگنال شناخته شده است.
منفی کاذب (FN) معادل سیگنال گمشده (miss) یا «خطای نوع دوم» (Type II Error) در آزمون فرض آماری است. به این ترتیب دستگاه دریافت کننده، نتوانسته سیگنال موجود را شناسایی کند.

حال محاسبات مربوط به نسبت یا نرخ‌های مختلف برحسب این مقادیر را مطابق با جدول زیر معرفی می‌کنیم.

جدول ۲: اندیس‌های شناسایی نرخ یا نسبت دسته‌بندی صحیح

نام شاخص	شرح	نحوه محاسبه
Sensitivity, recall, hit rate, or true positive rate (TPR)	حساسیت، بازیابی، نرخ اصابت یا نرخ مثبت صحیح	$\mathrm {TPR} = \dfrac{TP}{P} = \dfrac{TP}{TP + FN} = 1 - FNR$
Specificity, selectivity or true negative rate (TNR)	ویژگی، گزینشی یا نرخ منفی صحیح	$\mathrm {TNR} = \dfrac{TN}{N} = \dfrac{TN}{TN + FP} = 1 - FPR$
Precision or positive predictive value (PPV)	دقت، مقدار پیش‌بینی مثبت	$\mathrm {PPV} = \dfrac{TP}{TP+FP} = 1-FDR$
Negative predictive value (NPV)	مقدار پیش بینی منفی	$\mathrm {NPV} = { \frac {\mathrm {TN} }{\mathrm {TN} + \mathrm {FN} }} = 1 - \mathrm {FOR}$
Miss rate or false negative rate (FNR)	نرخ گمشدن سیگنال یا نرخ منفی کاذب	$\mathrm {FNR} = { \frac { \mathrm {FN} }{ \mathrm {P} }} = { \frac { \mathrm {FN} }{ \mathrm {FN} + \mathrm {TP} }} = 1 - \mathrm {TPR}$
Fall-out or false positive rate (FPR)	خطا یا نرخ مثبت کاذب	$\mathrm {FPR} = { \frac { \mathrm {FP} }{ \mathrm {N} }} = { \frac { \mathrm {FP} }{ \mathrm {FP} + \mathrm {TN} }} = 1 - \mathrm {TNR}$
False discovery rate (FDR)	نرخ کشف کاذب	$\mathrm {FDR} = {\frac {\mathrm {FP} }{\mathrm {FP} + \mathrm {TP} }} = 1 - \mathrm {PPV}$
False omission rate (FOR)	نرخ حذف خطا	$\mathrm {FOR} = { \frac { \mathrm {FN} }{\mathrm {FN} + \mathrm {TN} }} = 1 - \mathrm {NPV}$
Prevalence Threshold (PT)	آستانه شیوع	$\mathrm{PT} = { \frac {{ \sqrt {TPR( - TNR + 1)}} + TNR - 1 }{(TPR + TNR - 1 )}}$
Threat score (TS) or critical success index (CSI)	نمره تهدید یا شاخص موفقیت بحرانی	$\mathrm {TS} = { \frac { \mathrm {TP} }{\mathrm {TP} + \mathrm {FN} + \mathrm {FP} }}$

همچنین شاخص‌های ارزیابی دسته‌بندی نیز می‌تواند به یکی از روش‌های معرفی شده در جدول ۳، مورد محاسبه قرار گیرد. واضح است که پارامترهای مورد استفاده، باید از جدول ۲ استخراج شوند.

جدول ۳: شاخص‌های ارزیابی دسته‌بندی

نام شاخص	شرح	نحوه محاسبه
Accuracy (ACC)	صحت یا دقت	$\mathrm {ACC} = {\frac {\mathrm {TP} + \mathrm {TN} }{ \mathrm {P} + \mathrm {N} }} = { \frac {\mathrm {TP} + \mathrm {TN} }{ \mathrm {TP} + \mathrm {TN} + \mathrm {FP} + \mathrm {FN} }}$
Balanced accuracy (BA)	صحت یا دقت متعادل	$\mathrm {BA} = { \frac {TPR + TNR}{2}}$
F1 score	امتیاز اف وان- میانگین توافقی دقت و حساسیت	$\mathrm {F} _{1} = 2\cdot { \frac { \mathrm {PPV} \cdot \mathrm {TPR} }{\mathrm {PPV} + \mathrm {TPR} }} = { \frac {2 \mathrm {TP} }{2 \mathrm {TP} + \mathrm {FP} + \mathrm {FN} }}$
Matthews correlation coefficient (MCC)	ضریب همبستگی ماتیوس	$\mathrm {MCC} = {\frac {\mathrm {TP} \times \mathrm {TN} - \mathrm {FP} \times \mathrm {FN} }{\sqrt {(\mathrm {TP} + \mathrm {FP} )(\mathrm {TP} + \mathrm {FN} )(\mathrm {TN} + \mathrm {FP} )(\mathrm {TN} + \mathrm {FN} )}}}$
Fowlkes–Mallows index (FM)	شاخص فولکس-مالوز	$\mathrm {FM} = {\sqrt {{ \frac {TP}{TP + FP}} \cdot { \frac {TP}{TP + FN}}}} = { \sqrt {PPV\cdot TPR}}$
Informedness or bookmaker informedness (BM)	آگاهی بخشی یا نشانگر آگاهی بخشی	$\mathrm {BM} = \mathrm {TPR} + \mathrm {TNR} - 1$
Markedness (MK) or deltaP	علامت‌داری یا دلتای پی	$\mathrm {MK} =\mathrm {PPV} +\mathrm {NPV} - 1$

فضای ROC

جدول ۱ که یک جدول توافقی است، می‌تواند شاخص‌های متعددی برای ارزیابی دسته‌بندی ارائه کند که بیشتر آن‌ها را در جدول ۲ و ۳ مشاهده کردید. ولی برای ترسیم نمودار یا منحنی ROC فقط به «نرخ مثبت صحیح» (TPR) و «نرخ مثبت کاذب» (FPR) احتیاج داریم.

به این ترتیب TPR مشخص می‌کند که به چه نسبتی پیش‌بینی صحیح صورت گرفته است. یعنی تعداد پیش‌بینی‌های صحیح بر تعداد نتایج مثبت واقعی تقسیم شده و نرخ پیش‌بینی صحیح مثبت محاسبه می‌شود. از طرف دیگر FPR نشانگر تعداد شناسایی‌های مثبت از میان مشاهدات منفی است. این نسبت نیز به عنوان نرخ مثبت کاذب در نمودار ROC به کار می‌رود.

بنابراین فضای ROC بوسیله این دو شاخص یعنی FPR روی محور افقی و TPR روی محور عمودی شکل داده می‌شود. در نتیجه یک توازن بین سود (TP) و هزینه (FP) روی نمودار ROC، شکل می‌گیرد. توجه داشته باشید که هر عنصر از «ماتریس درهم‌ریختگی» (Confusion Matrix) یک نقطه در منحنی ROC را تشکیل می‌دهد.

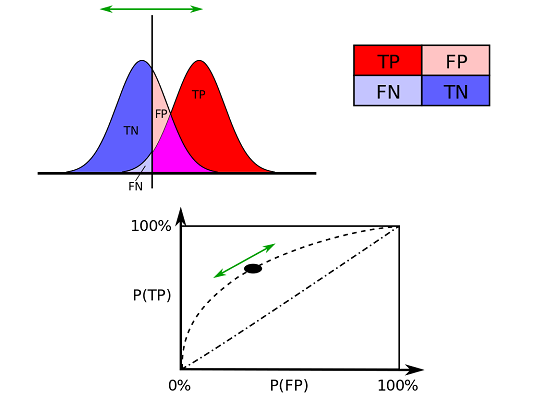
به تصویر ۲ توجه کنید، بهترین عملکرد دسته‌بندی در این نمودار در نقطه‌ای با مختصات $(0,1)$ رخ خواهد داد که در آن کمترین نرخ اشتباه و بیشترین نرخ بازیابی یا حساسیت را داریم. این نقطه بیانگر «بهترین دسته‌بندی» (Perfect Classification) است.

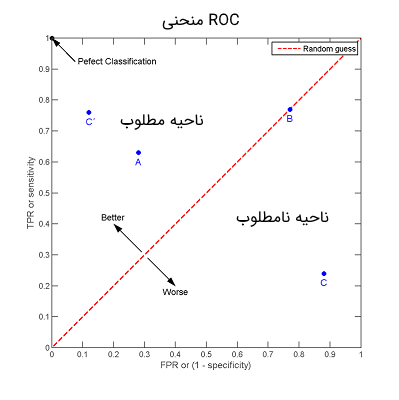
ROC space — تصویر ۲: نواحی مطلوب و نامطلوب در منحنی ROC

خطوط منقطعی که از میان نمودار عبور کرده و نقطه $(0,0)$ را به $(1,1)$ پیوند می‌دهند، حدس تصادفی است که به صورت ناحیه ۵۰٪-۵۰٪ نیز شناخته می‌شوند. اگر نقطه‌ای روی این خطوط منقطع قرار گرفته باشد، تشخیص درستی نسبت به قرارگیری در هر گروه، برایش وجود ندارد. در حقیقت در نیمی از موارد می‌تواند در یک دسته و در نیمی از موارد نیز در دسته دیگری، طبقه‌بندی ‌شود و نقشی در تعیین خطا نخواهد داشت. یکی از نمونه‌های معروف برای دسته‌بندی به صورت تصادفی، تصمیم تعلق نقطه به هر یک از دو گروه بوسیله پرتاب سکه است. هر چه تعداد نمونه‌ها در دسته‌بند تصادفی بیشتر شود، این خط به قطر نواحی ROC نزدیکتر خواهد شد. اگر سکه نااریب باشد، این خط از نقطه $(0.5,0.5)$ ‌ عبور خواهد کرد.

مطابق با تصویر ۲، این خط قطری، فضای ROC را به دو بخش تقسیم می‌کند. ناحیه بالای این خط، ناحیه مطلوب (بهتر از دسته‌بندی تصادفی) و ناحیه نامطلوب (بدتر از دسته‌بندی تصادفی) این بخش‌ها را تشکیل می‌دهند. برای روشن شدن موضوع در ادامه به یک مثال در این زمینه می‌پردازیم.

رسم نمودار ROC برای یک دسته‌بند دو دویی

فرض کنید ۱۰۰ مشاهده در گروه P و ۱۰۰ نمونه بعدی در دسته N از یکدیگر جدا شده‌اند. قرار است بدون توجه به این وضعیت آن‌ها را به دو دسته، طبقه‌بندی کنیم. در این بین سه روش (از A تا C) برای دسته‌بندی این نمونه‌ها به کار رفته است. تصویر زیر مقادیر شاخص‌های محاسباتی منحنی ROC برای آن‌ها را مشخص کرده است.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

نکته: روش 'C، متمم روش C است به این معنی که جای سطرهای جدول توافقی آن با یکدیگر جابجا شده است. به این ترتیب هر جا روش C، مشاهده‌ای را در گروه اول جای دهد، روش 'C آن را در گروه ۲ در نظر می‌گیرد و برعکس.

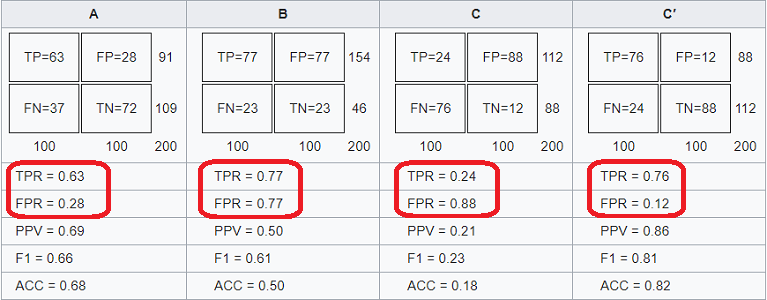
classified method results — تصویر ۳: شاخص‌های محاسباتی برای منحنی ROC برحسب چهار روش دسته‌بندی

بر اساس رای ۵۷ نفر

آیا این مطلب برای شما مفید بود؟

اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.

ثبت نظر

منابع:

Wikipedia مجله فرادرس

آرمان ری بد (+)

«آرمان ری‌بد» دکتری آمار در شاخه آمار ریاضی دارد. از علاقمندی‌های او، یادگیری ماشین، خوشه‌بندی و داده‌کاوی است و در حال حاضر نوشتارهای مربوط به آمار و یادگیری ماشین را در مجله فرادرس تهیه می‌کند.

۱۶ دیدگاه برای «منحنی ROC و کاربردهای آن — به زبان ساده»

مجتبی ساعی

۱۷ خرداد، در ۱۴۰۲ ۱۱:۳۵ ق.ظ

با سلام و خسته نباشید بسیار عالی توضیح داده شده
ممنون

پاسخ

علی

۰۸ دی، در ۱۴۰۱ ۱:۴۴ ق.ظ

با سلام
لطفا کتاب یا مرجع معتبر برای رفرنس دهی در مقاله به این موضوع را در صورت امکان معرفی بفرمایید.

پاسخ

ممد

۰۲ شهریور، در ۱۴۰۱ ۹:۳۶ ق.ظ

کارایی الگوریتم‌های «دسته‌بندهای دو دویی» (‌Binary Classifier) معمولا توسط شاخص‌هایی به نام «حساسیت» (Sensitivity) یا «بازیابی» (Recall) سنجیده می‌شود. اما در نمودار ROC هر دوی این شاخص‌ها ترکیب شده و به صورت یک منحنی نمایش داده می‌شوند.

«بازیابی و حساسیت» دو اسم برای یک مفهموم هستن.
specificity و recall باید نوشته بشه.

پاسخ

بابک خوش‌نویس

۰۷ شهریور، در ۱۴۰۱ ۱۱:۱۹ ق.ظ

با سلام و احترام؛

صمیمانه از همراهی شما با مجله فرادرس و ارائه بازخورد سپاس‌گزاریم.

این مورد اصلاح شد.

برای شما آرزوی سلامتی و موفقیت داریم.

سارینا

۱۶ آذر، در ۱۴۰۰ ۱۲:۲۳ ق.ظ

با عرض سلام و خسته نباشید. جواب این سوال رو من هیچ جا پیدا نکردم. روش ROC از آزمون های پارامتری به حساب می آید یا غیر پارامتری؟

پاسخ

ابوالفضل

۲۷ بهمن، در ۱۴۰۰ ۱۰:۲۹ ب.ظ

بنظرم شما میتونی ROC رو همه جا استفاده کنی. فقط کافیه یه سطح ترشولد داشته باشی برای کلاسیفیکیشن. اونوقت میتونی حساسیت و دقت رو محاسبه کنی. به عبارت دیگه هرجا تونستی حساسیت و دقت رو محاسبه کنی ROC رو هم داری

فرشید شیرافکن

۰۵ خرداد، در ۱۴۰۰ ۱۲:۴۱ ق.ظ

سلام .
واقعا عالی

پاسخ

فاطمه

۱۷ شهریور، در ۱۴۰۱ ۱۲:۴۰ ب.ظ

عه ی هم کلاسی لیسانس به این اسم داشتم 🙂
اره واقعا مطلب مفید و مختصری بود

ُزهرا میرصانعی

۰۹ فروردین، در ۱۴۰۰ ۲:۵۴ ب.ظ

با سلام و تشکر بابت مطالب توضیح داده شده
متاسفانه یه مشکلی ک در تدریس مباحث
امار وجود داره اینه که برای ما بیولوژیست ها درک مفاهیمش سخته… چون مثال ها همه از دامنه ی ریاضیات و اماره…و در مفهوم بیولوژی اصلا منتقل نمیشه

و دوم اینکه: خب اصلا چرا باید نمودار راک ترسیم بشه، چرا باید از یک تفریق بشه…ترسیم این نمودار چه مشکلی رو از داده ها حل میکنه که استفاده میشه؟ چرا از همون نمودار حساسیت و ویژگی استفاده نمیشه…
اینها مفاهیم پایه ای هست که من بعنوان یک خواننده اول باید بدونم مشکل چیه…تا بعد راه حلی که ارائه میشه برام قابل درک بشه.

باز هم از مدرس گرامی و تیم فرادرس ممنونم.

پاسخ

Freddy

۱۳ بهمن، در ۱۳۹۹ ۱:۰۷ ب.ظ

با سلام بسیار عالی و کاربردی

پاسخ

تینا

۰۵ بهمن، در ۱۳۹۹ ۲:۲۶ ب.ظ

با عرض سلام و تشکر خدمت شما. این مطلب بسیار مفید بود و من بسیار از این مطلب راضی هستم.

پاسخ

اسدی

۱۹ دی، در ۱۳۹۹ ۱۲:۲۴ ب.ظ

با سلام و تشکر فراوان.من از حضورتون سوال داشتم که در این متن نتونستم متوجه بشم و اینکه اگر داده های متغیر تست رنج داشته باشه و ما آنها را با دو کد مثیت یعنی یک و منفی یا دو تقسیم کنیم آیا در نقاط برش مشکلی ایجاد نمیشود.

پاسخ

علی

۲۶ شهریور، در ۱۳۹۹ ۱:۳۳ ق.ظ

با تشکر از جناب دکتر ری بد که چنین مقاله‌ی ارزشمندی را ارائه کردن.
جسارتا فقط سه تا مساله‌ی جزئی به نظرم اومد گفتم شاید لازم باشه تصحیح بشه
1. در جدول یک، به جای NP به نظرم اومد که FP نوشته بشه
2. در جدول دوم، ردیف سوم، فکر می‌کنم فرمول PPV جابجا نوشته شده
3. در فرمول نرخ مثبت صحیح انتگرال، قسمت TPR که اندیسf، برابر x نوشته شده فکر میکنم منظور متن، f1 باشه.

با سپاس فراوان از گروه فرادرس

پاسخ

آرمان ری بد

۲۶ شهریور، در ۱۳۹۹ ۸:۴۰ ق.ظ

سلام و وقت بخیر،
از تذکرهای به جا و موثر شما سپاسگزارم.
اصلاحات و اشتباه‌های نگارشی، به صورت درست درآمد و امیدوارم که متن مشکل دیگری نداشته باشد.

از این که همراه مجله فرادرس هستید، بر خود می‌بالیم.
خرسند و پاینده باشید.