قضیه مقدار میانگین (Mean Value Theorem) — به زبان ساده

در ریاضیات، قضیه مقدار میانگین به طور صریح بیان می‌کند که برای هر دو نقطه روی یک منحنی، حداقل یک نقطه وجود دارد که خط مماس بر آن نقطه موازی وتری است که آن دو نقطه را به هم وصل می‌کند. شاید بتوان این قضیه را مهم‌ترین قضیه در رابطه با توابع پیوسته در حسابان (حساب دیفرانسیل و انتگرال) در نظر گرفت. قضیه‌های مختلف و متنوعی نیز براساس قضیه مقدار میانگین ساخته شده است که در زمینه‌های مختلف کاربرد دارند. سادگی بیان این قضیه از اهمیت آن نمی‌کاهد، بطوری که با استفاده از آن بسیاری از مباحث، روشن و قابل اثبات می‌شوند.

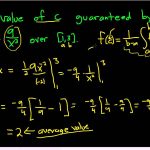
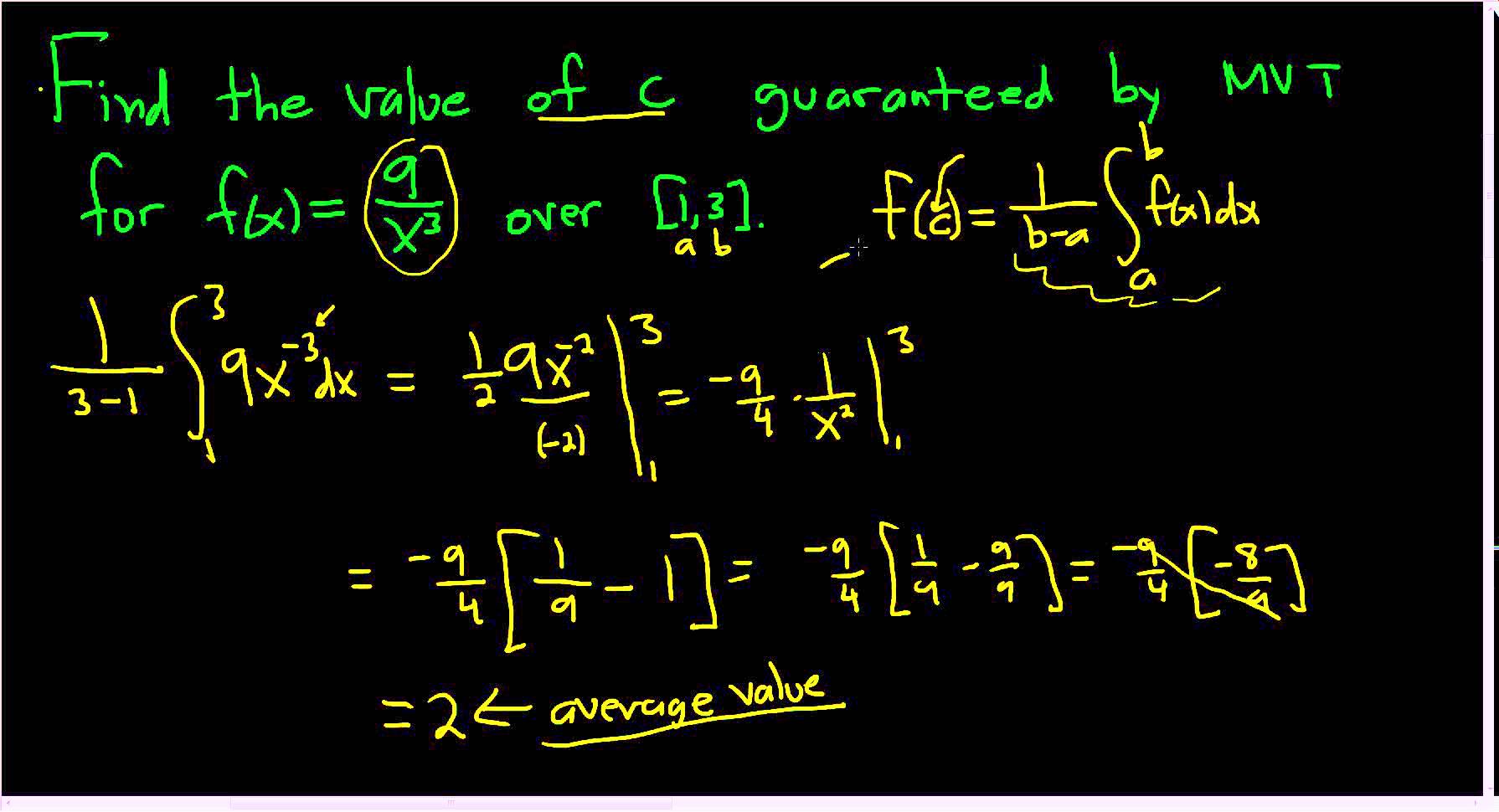
با توجه به اینکه برای آشنایی با این قضیه و قضیه مشابه آن (قضیه رول) باید با مفاهیم مشتق و پیوستگی تابع آشنا باشید، مطالعه مطالب مشتق — به زبان ساده و پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده ضروری به نظر می‌رسد. همچنین به منظور آگاهی از تعریف تابع و خصوصیات آن مرور نوشتار مفاهیم تابع – به زبان ساده خالی از لطف نیست.

قضیه مقدار میانگین

رفتار تابع‌ها بسیار مهم هستند. هرچه خصوصیات تابع بهتر شناخته شود، بهتر می‌توان رفتار آن را پیش‌بینی کرد. یکی از قضیه‌های مهم که در مورد خصوصیات تابع وجود دارد، «قضیه مقدار میانگین» (Mean Value Theorem) است. البته این قضیه حالت کلی‌تری از «قضیه رول» (Roll's Theorem) محسوب می‌شود.

فیلم آموزش مبانی آنالیز ریاضی – جامع و کاربردی در فرادرس

کلیک کنید

«میچل رول» (Michel Rolle) ریاضیدان فرانسوی ابتدا قضیه رول را براساس چندجمله‌ای‌ها به کمک روش هندسی در سال 1691 اثبات کرد. او که به حساب دیفرانسیل و انتگرال علاقه‌ای نداشت، قضیه‌ای را اثبات کرد که در رشد این شاخه از ریاضیات موثر بود. گفته می‌شود که درک اصلی از صورت این قضیه توسط «باهاسکارای دوم» (Bhaskara II) ریاضی‌دان هندی، در قرن ۱۱ میلادی صورت گرفته ولی بعدها توسط «آگوستین کوشی» (Augustin Louis Cauchy) دانشمند ریاضی و آمار در سال 1823 به صورت کامل‌تری از روش رول، اثبات شد. او نشان داد که قضیه رول حالت خاصی از قضیه مقدار میانگین است. بنابراین برای شروع کار بهتر است ابتدا در مورد قضیه رول بحث کرده و سپس به قضیه مقدار میانگین بپردازیم.

قضیه رول (Rolle's Theorem)

صورت قضیه رول: اگر f تابعی حقیقی مقدار و پیوسته روی بازه $$[a,b]$$ و مشتق‌پذیر روی بازه $$(a,b)$$ باشد، بطوری که $$f(a)=f(b)$$، آنگاه مقداری مانند c در بازه $$(a,b)$$ وجود دارد که $$f'(c)=0$$ باشد.

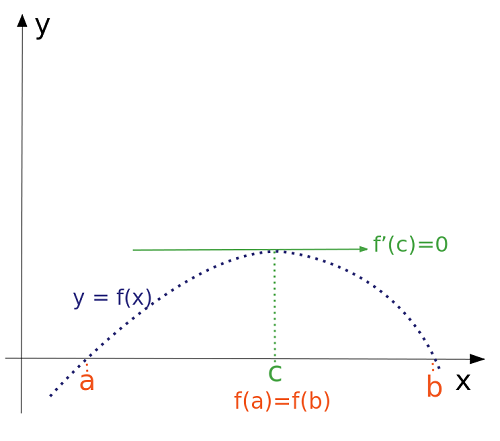
همانطور که در نمودار بالا دیده می‌شود، نقطه c محلی از بازه $$(a,b)$$ است که خط مماس برمنحنی یا تابع $$f(x)$$ به موازات محور افقی قرار می‌گیرد. همچنین مشخص است که در نقطه a و b مقدار تابع یکسان است.

نکته: می‌توانیم فرض کنیم که مقدار $$f(a)=f(b)=0$$ ولی اگر چنین نباشد می‌توان قضیه را برای تابعی به صورت $$f(x)-r$$ اثبات کرد که در آن r اختلاف مقدار تابع f با صفر است. یعنی $$f(a)-r=f(b)-r=0$$.

اثبات: برای اثبات قضیه رول دو حالت در نظر می‌گیریم. یا تابع f در همه بازه $$(a,b)$$ صفر است یا در این بازه تغییر می‌کند.

حالت اول: اگر در همه نقاط بازه $$(a,b)$$ تابع f، صفر باشد که قضیه ثابت است. زیرا در نقطه c در این بازه هم مقدار تابع صفر بوده و مشتق آن نیز برابر با صفر خواهد بود.

حالت دوم: اگر تابع در این بازه تغییر کند، ممکن است مقدار آن در بعضی مواقع مثبت و در بعضی از نقاط نیز منفی باشد. از طرفی می‌دانیم که برای یک تابع پیوسته، در یک فاصله حتما مقدار کمینه و بیشنیه (Minimum, Maximum) وجود دارد. این نقاط کمینه یا بیشینه یا در نقاط انتهای فاصله قرار دارند یا در نقطه‌ای هستند که مشتق تابع f برابر با صفر است که به آن نقطه بحرانی می‌گوییم.

ابتدا نقاطی از بازه $$(a,b)$$ را در نظر بگیرید که تابع در آن مثبت است. طبق قضیه مقدار میانی حتما مقداری در این فاصله $$(a,b)$$ وجود دارد که تابع را ماکزیمم می‌کند. چون $$f(a)=f(b)=0$$ پس نقاط a و b نمی‌توانند مربوط به ماکزیمم تابع باشند. پس نقطه‌ای مانند c وجود دارد که یکی از دو نقطه انتهایی a و یا b نیست و تابع را ماکزیمم می‌کند. بنابراین باید داشته باشیم f'(c)=0 و از طرفی $$f(c)>0$$. حال نقاطی در بازه $$(a,b)$$ را در نظر بگیرید که تابع در آن نقاط منفی است. باز هم طبق قضیه مقدار میانی، حتما مقداری در فاصله بازه $$(a,b)$$ مثل c وجود دارد که تابع f را کمینه می‌کند زیرا تابع پیوسته است. پس داریم $$f(c)<0$$ و f'(c)=0. به این ترتیب وجود چنین نقطه‌ای اثبات شد.

نکته: اگر f(c)=f(a)=f(b)=0 باشد، نتیجه می‌گیریم که تابع f مقدار ثابتی دارد. پس به حالت اول در اثبات بر می‌گردیم.

صورت قضیه مقدار میانگین

این قضیه روشن می‌کند که برای یک تابع پیوسته و مشتق‌پذیر روی بازه (a,b) حتما نقطه‌ای مانند c پیدا می‌شود که می‌توان رابطه زیر را برای آن نوشت:

$$\large \displaystyle f'(c)=\frac {f(b)-f(a)}{b-a}$$

اگر وتر بین دو نقطه a و b را با Secant (با رنگ نارنجی) و خط مماس بر منحنی $$f(x)$$ در نقطه c را با Tangent (رنگ سبز) نشان دهیم، تصویر زیر به خوبی قضیه را توصیف می‌کند.

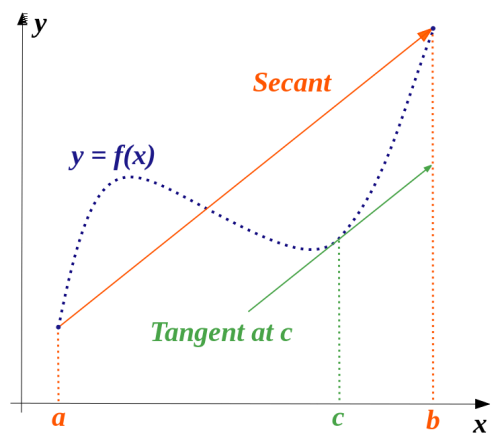
همانطور که دیده می‌شود خط مماس بر منحنی در نقطه c موازی با وتر ترسیم شده بین دو نقطه a و b است. البته توجه داریم که تابع $$f(x)$$ در بازه $$[a,b]$$ باید پیوسته و در فاصله $$(a,b)$$ نیز مشتق‌پذیر باشد. این شرایط، فرضیات قضیه مقدار میانگین را تشکیل می دهند.

تفسیر هندسی قضیه مقدار میانگین

اگر خط وتری که منحنی تابع پیوسته f را دو نقطه a و b به یکدیگر متصل می‌کند در نظر بگیریم، حتما نقطه‌ای در بین دو نقطه a و b وجود دارد که شیب خط مماس بر منحنی در این نقطه، برابر با شیب خط وتر ترسیم شده از دو نقطه $$(a,f(a))$$ و $$(b,f(b))$$ است. به این ترتیب شکل رسمی برای قضیه مقدار میانگین را می‌توان به صورت زیر نوشت:

فرم رسمی قضیه مقدار میانگین

فرض کنید تابع f از بازه $$[a,b]$$ به اعداد حقیقی تعریف شده باشد. یعنی داشته باشیم:

$$\large \displaystyle f:[a,b]\to \mathbb {R}$$

اگر این تابع در بازه بسته $$[a.b]$$ پیوسته و در بازه $$(a,b)$$ مشتق‌پذیر باشد ($$a$$)، آنگاه نقطه‌ای مانند c در $$(a,b)$$ وجود خواهد داشت که:

$$\large \displaystyle f'(c)=\frac {f(b)-f(a)}{b-a}$$

در تصویر زیر مشخص است که تعداد نقاط c ممکن است یک با بیشتر باشند.

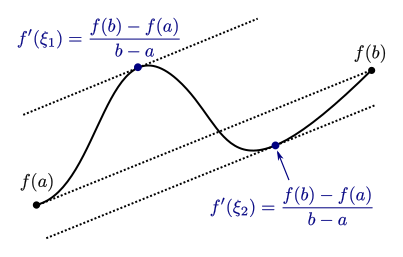
نکته: این قضیه برای توابع حقیقی مقدار تعریف شده و صحت دارد. در صورتی که تابع f تابع یا مقدارهای مختلط باشد دیگر نمی‌توان از چنین قضیه‌ای استفاده کرد. زیرا برای مثال اگر تابع را به صورت $$f(x)=e^{ix}$$ در نظر بگیریم که x یک عدد حقیقی است، آنگاه مشخص است که:

$$\large \displaystyle f(2\pi )-f(0)=0=0(2\pi -0)$$

در حالیکه مقدار مشتق چنین تابعی هرگز صفر نخواهد شد.

$$\large \displaystyle f'(x)\neq 0 \forall x \in \mathbb {R}$$

اثبات قضیه مقدار میانگین

مشخص است که منظور از $$\frac {f(b)-f(a)}{b-a}$$ شیب خطی است که دو نقطه $$\displaystyle (a,f(a)) و \displaystyle (b,f(b))$$ را به یکدیگر متصل می‌کند. به چنین خطی وتر منحنی f بر دو نقطه a و b گفته می‌شود. از طرف دیگر $$f'(x)$$ نیز شیب خط مماس بر منحنی در نقطه $$(x,f(x))$$ را نشان می‌دهد.

فیلم آموزش مشتق گیری در مبانی آنالیز ریاضی (رایگان) در فرادرس

کلیک کنید

تابع $$g(x)=f(x)-rx$$ را در نظر بگیرید که در آن r یک ثابت است. از آنجایی که تابع f روی $$[a,b]$$ پیوسته و روی $$(a,b)$$ مشتق‌پذیر است،‌ همین خصوصیات را برای تابع g هم خواهیم داشت. زیرا تفاضل دو تابع پیوسته نیز پیوسته و تفاضل دو تابع مشتق‌پذیر نیز در بازه مشترکشان مشتق‌پذیر است. دامنه مشترک برای هر دو تابع f و rx همان بازه $$[a,b]$$ و یا $$(a,b)$$ خواهد بود.

حال با تعیین مقدار r سعی می‌کنیم قضیه مقدار میانگین را به کمک قضیه رول اثبات کنیم. در نتیجه خواهیم داشت:

$$\large \displaystyle \begin{aligned}g(a)=g(b)&\iff f(a)-ra=f(b)-rb\\&\iff r(b-a)=f(b)-f(a)\\&\iff r={\frac {f(b)-f(a)}{b-a}}\cdot \end{aligned}$$

به این ترتیب تابع g در شرایط قضیه رول صدق می‌کند و می‌توان نقطه‌ای در بازه $$(a,b)$$ مانند c پیدا کرد که $$g'(c)=0$$. حال به کمک محاسبه مشتق تابع g برحسب تابع f می‌توان نوشت:

$$\large \displaystyle \begin{aligned}&g'(x)=f'(x)-r\\&g'(c)=0\\&g'(c)=f'(c)-r=0\\&\Rightarrow f'(c)=r={\frac {f(b)-f(a)}{b-a}}\end{aligned}$$

یک کاربرد ساده

فرض کنید تابع f،‌ حقیقی مقدار و روی بازه T از اعداد حقیقی پیوسته باشد. اگر مشتق این تابع در همه نقاط داخلی فاصله T موجود و برابر با صفر باشد، آنگاه تابع f در این بازه مقداری ثابت است.

اثبات: فرض کنید که فاصله $$(a,b)$$ یک فاصله اختیاری از T باشد. براساس قضیه مقدار میانگین، نقطه‌ای مانند c در این فاصله وجود دارد که:

$$\large \displaystyle 0=f'(c)=\frac {f(b)-f(a)}{b-a}$$

پس نتیجه می‌گیریم که $$f(a)=f(b)$$ است. بنابراین تابع f روی نقاط داخلی فاصله T ثابت و همچنین روی T پیوسته است. از آنجایی که این فاصله اختیاری بود می‌توان نتیجه گرفت که برای هر فاصله‌ای از T مقدار $$f(c)$$ ثابت است.

نکته: در این اثبات، فقط پیوستگی تابع روی نقاط انتهایی فاصله T مورد نظر است. زیرا مشتق‌پذیری درون نقاط فاصله T باعث پیوستگی تابع درون فاصله T خواهد بود.

قضیه مقدار میانگین کوشی

کوشی، قضیه مقدار میانگین را تعمیم داد و براساس دو تابع f و g نوشت. او شرط پیوستگی و مشتق‌پذیری را برای هر دو تابع در نظر گرفت.

صورت قضیه مقدار میانگین کوشی

اگر f و g دو تابع پیوسته روی بازه $$[a,b]$$ و مشتق‌پذیر روی فاصله $$(a,b)$$ باشند، آنگاه نقطه‌ای مانند c در بازه $$(a,b)$$ وجود دارد که برایش رابطه زیر برقرار است:

$$\large {\displaystyle (f(b)-f(a))g'(c)=(g(b)-g(a))f'(c)}$$

نکته: اگر در رابطه بالا، مقدار تابع g در دو نقطه ابتدای و انتهای فاصله یکسان و مقدار مشتق تابع g در نقطه c نیز مخالف صفر باشد، رابطه بالا به صورت زیر درخواهد آمد.

$$\large {\displaystyle {\frac {f'(c)}{g'(c)}}={\frac {f(b)-f(a)}{g(b)-g(a)}}}$$

تفسیر هندسی قضیه مقدار میانگین کوشی

قضیه مقدار میانگین کوشی از دیدگاه هندسی بیان می‌دارد که خط مماس برای نمودار منحنی زیر:

$$\large {\displaystyle {\begin{cases}[a,b]\to \mathbf {R} ^{2}\\t\mapsto (f(t),g(t))\end{cases}}}$$

موازی خط وتر رسم شده از نقطه $$f(a),g(a)$$ تا $$f(b),g(b)$$ خواهد بود.

به بیان دیگر اگر فرض کنید در فضای دو بعدی از اعداد حقیقی منحنی با نقاط $$(f(x),g(x))$$ وجود دارد که در آن x یک عدد حقیقی است و f و g نیز در فاصله بسته a تا b پیوسته و در فاصله باز a تا b مشتق‌پذیر هستند. آنگاه نقطه‌ای در این فاصله مانند c وجود دارد که خط مماس بر منحنی $$(f(x),g(x))$$ در آن نقطه (یعنی در نقطه $$(f(c),g(c))$$ از منحنی) موازی خط وتر رسم شده از نقطه $$(f(a),g(a))$$ تا $$(f(b),g(b))$$ خواهد بود.

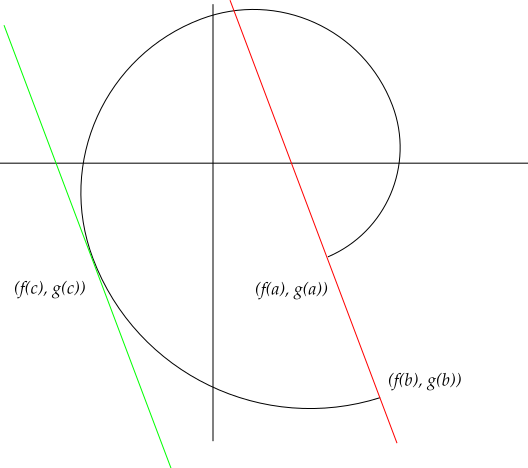
نکته: براساس قضیه مقدار میانگین کوشی به نظر می‌رسد که قضیه مقدار میانگین حالت خاصی از قضیه مقدار میانگین کوشی باشد اگر در قضیه کوشی g(x)=x باشد.

قضیه مقدار میانگین برای انتگرال معین

از قضیه مقدار میانگین در محاسبه انتگرال نیز می‌توان کمک گرفت. فرض کنید که تابع f روی بازه $$[a,b]$$ پیوسته باشد.

فیلم آموزش مبانی آنالیز ریاضی – مرور و حل تست کنکور ارشد – بخش دوم در فرادرس

کلیک کنید

در این حالت مقداری مانند c در فاصله $$(a,b)$$ وجود دارد که:

$$\large {\displaystyle \int _{a}^{b}f(x)\,dx=f(c)(b-a)}$$

از آنجایی که مقدار متوسط تابع f روی بازه $$(a,b)$$ به صورت زیر تعریف می شود:

$$\large {\displaystyle {\frac {1}{b-a}}\int _{a}^{b}f(x)\,dx}$$

می‌توان قضیه مقدار میانگین برای انتگرال را به این شکل بیان کرد که میانگین یا متوسط تابع f روی بازه $$(a,b)$$ برابر با مقدار تابع در نقطه c است که در رابطه بالا صدق کند. تصویر زیر به خوبی این رابطه را نشان می‌دهد.

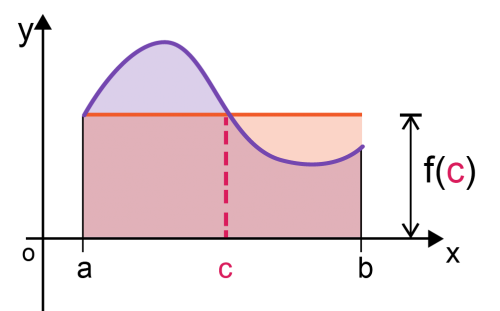
برای وضوح بیشتر کاربرد قضیه میانگین در انتگرال، بحث را ادامه می‌دهیم. همانطور که پیش‌تر در وبلاگ فرادرس در  مطلبی تحت عنوان انتگرال — به زبان ساده اشاره شده است، منظور از انتگرال یک تابع در بازه a تا b می‌تواند اندازه سطح زیر منحنی مربوط به آن تابع باشد. به این ترتیب همانطور که در تصویر بالا دیده و مشخص شده است، سطح زیر منحنی که به رنگ بنفش درآمده با مساحت مستطیلی نارنجی رنگ برابر است. پس مساحت مستطیلی که طول آن برابر با طول فاصله a تا b و عرض آن برابر با $$f(c)$$ باشد با انتگرال تابع f روی بازه a تا b یکسان محسوب می‌شود. این مسئله، یکی از کاربردهای مهم قضیه مقدار میانگین برای انتگرال و تابع f است زیرا طبق قضیه اصلی حساب دیفرانسیل و انتگرال، مشتق انتگرال تابع f همان تابع f است اگر تابع f روی بازه a تا b انتگرال پذیر و انتگرال آن نیز مشتق‌پذیر باشد. بنابراین شرایط قضیه مقدار میانگین بین تابع f و انتگرالش برقرار است. یعنی خواهیم داشت:

$$\large \dfrac{\int f(x)dx}{dx}=f(x)$$

پس در اینجا به نظر می‌رسد، اگر بخواهیم با نمادهای قضیه مقدار میانگین کار کنیم، تابع f در قضیه مقدار میانگین همان انتگرال تابع f یعنی $$h(x)=\int f(x)dx$$ است و مشتق آن در نقطه c نیز همان مقدار مشتق این تابع در نقطه c یعنی $$h'(c)=f(c)$$ است. دراین صورت رابطه به شکل زیر درخواهد آمد:

$$\large {\displaystyle {h'(c)=f(c)=\frac {1}{b-a}}\int _{a}^{b}f(x)\,dx}=\dfrac{h(b)-h(a)}{b-a}$$

که صورت قضیه مقدار میانگین برای تابع h است.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه‌ی ریاضیات، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه‌ آموزش‌های ریاضی و فیزیک
• مجموعه‌ آموزش‌های دبیرستان و پیش‌دانشگاهی
• چندجمله‌ای‌ها – به زبان ساده
• معادله های پارامتری — به زبان ساده
• پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده
• معادلات و نامعادلات ریاضی — پیدایش و کاربردها
• معادلات خطی (Linear Equations) — به زبان ساده
• معادله درجه دو — به زبان ساده
• قضیه اساسی جبر — به زبان ساده

^^