فضای اقلیدسی و خصوصیات آن — به زبان ساده

فضای اقلیدسی (Euclidean Space) به عنوان یک فضای پایه در ریاضیات، جایگاهی مهمی دارد. مختصات دکارتی و استفاده از آن در ابعاد بزرگتر از دو بعد و محاسباتی برداری همگی بر اساس این فضا شکل گرفته‌اند. به همین منظور در این نوشتار به فضای اقلیدسی و خصوصیات آن خواهیم پرداخت. ابتدا مفهوم فضای برداری را به کمک مثال‌هایی بیان کرده، سپس ویژگی‌های چنین فضایی را متذکر می‌شویم.

برای آشنایی با موضوعات مربوط به این نوشتار بهتر است ابتدا با مفاهیم اصلی در نوشتارهای فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در داده‌کاوی و فضای متریک و نامساوی مثلثی — به زبان ساده آشنا شوید. همچنین خواندن مطالب فضای هیلبرت و خصوصیات آن و همچنین دستگاه مختصات دکارتی — به زبان ساده نیز خالی از لطف نیست.

فضای اقلیدسی و خصوصیات آن

معمولا فضای اقلیدسی را با فضا یا مختصات دکارتی در سه بعد یکسان در نظر می‌گیریم. در این مختصات می‌توان بردارهای سه بُعدی را نمایش داده و محاسبات مربوط به چنین بردارهایی را اجرا و نتایج را نشان داد.

فیلم آموزش مبانی آنالیز ریاضی – جامع و کاربردی در فرادرس

کلیک کنید

ولی در ریاضیات جدید، فضای اقلیدسی می‌تواند براساس ابعاد بیشتر نیز تعریف و به کار گرفته شود. این موضوع نشان می‌دهد که فضای سه بعدی و به کارگیری از صفحات دو بعدی در آن، به عنوان یک حالت خاص از فضای اقلیدسی مدرن در نظر گرفته می‌شود.

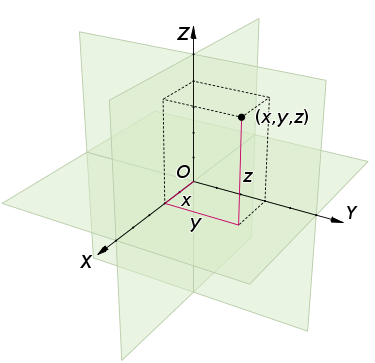
همانطور که می‌دانید چنین مختصاتی اولین بار توسط «اقلیدس اسکندری» (Euclid of Alexandria)  ابداع شد. او به تعریف صفحات در چنین فضای سه بُعدی پرداخت و از آن برای نمایش سطح‌ها و اثبات رابطه بین اعداد صحیح و بخش‌پذیری پرداخت. بطوری که امروزه برای پیدا کردن بزرگترین مقسوم علیه مشترک هم از روش اقلیدس استفاده می‌کنیم. او با ترکیب هندسه و ریاضیات گام موثری در ایجاد اصول در ریاضیات و هندسه برداشت.

او به کمک هندسه ابداعی خود سعی در توصیف حرکت سیاره‌ها و منضومه شمسی داشت. او سعی کرد هندسه خود را بر کمترین تعداد اصول بنا نهاده و بیشترین قضیه‌ها را به کمک آن‌ها اثبات کند.

برای مثال می‌توان از اصل (Postulate) عبور یک خط راست از بین دو نقطه یا عدم تقاطع دو خط موازی اسم برد.

بعدها و در اوایل قرن بیستم، «فضاهای برداری» (Vector Space) و «جبر خطی» (Linear Algebra) برای تعریف دقیق و کاربردی فضای اقلیدسی، مورد توجه قرار گرفت. به این ترتیب فضای اقلیدسی از هندسه خارج و به حوزه ریاضیات کاربردی تمایل پیدا کرد.

در سال ۱۶۳۷، رنه دکارت (Rene Descartes) با معرفی «مختصات دکارتی» (Cartesian Coordinates) نشان داد که مسائل هندسی را می‌توان بوسیله محاسبات ریاضی و اعداد نیز حل کرد. به این ترتیب هندسه به قسمتی از جبر به نام جبر خطی وارد شد. این گام مهم، باعث شد بسیاری از جنبه‌های ریاضیاتی نیز در هندسه به کار رود. یا این کار، اعداد به صورت مقادیری در این مختصات به شکل هندسی نمود پیدا کردند و هر شکل هندسی نیز به فرمی از اعداد (ماتریس موقعیت) در این مختصات نمایش داده شد.

بعد از قرن نوزدهم، دانشمندان و ریاضیدانان از هندسه اقلیدسی و مختصات دکارتی برای نمایش نقاط دارای بیش‌تر از ۳ بُعد نیز استفاده کرده و زمینه‌ساز ظهور «هندسه تحلیلی» (Analytic Geometry) شدند، بطوری که فضای برداری و جبر خطی نیز تحت تاثیر آن بوجود آمدند.

البته باید توجه داشته باشید که خصوصیاتی تعریف شده برای فضای اقلیدسی باعث بوجود آمدن گونه‌های مختلفی از فضای اقلیدسی شده است. ولی به هر حال، فضای اقلیدسی و انواع آن، از نقطه‌هایی تشکیل شده است که دارای خواص مشخصی هستند.

نکته جالب در مورد فضاهای اقلیدسی هم-بُعد، این است که همه آن‌ها یک ریخت (Isomorphic) هستند. این امر به این معنی است که در بیشتر مواقع کافی است که با فضای اعداد حقیقی $$n$$-بُعدی یا همان $$R^n$$ به همراه ضرب داخلی (Dot Product) کار کنیم.

خاصیت یک ریختی از فضای اقلیدسی به $$R ^ n$$ و به کارگیری نقطه‌های $$n$$-بُعدی به صورت $$n$$-تایی‌های مرتب ($$n-tuple$$) از اعداد حقیقی، در مختصات دکارتی به بهترین نحو مورد استفاده قرار گرفته است.

تعریف فضای اقلیدسی

به یاد دارید که اگر یک عملگر نسبت به مجموعه بسته باشد، آن مجموعه به همراه عملگرش، تشکیل فضا را می‌دهند. در ادامه این متن هم فضای اقلیدسی را براساس یک مجموعه و یک عملگر تعریف می‌کنیم.

فیلم آموزش هندسه دیفرانسیل در MATLAB (رایگان) در فرادرس

کلیک کنید

مجموعه $$R^n$$ شامل $$n$$-تایی‌های مرتب از اعداد حقیقی و ضرب نقطه‌ای یا ضرب داخلی یک فضای اقلیدسی $$n$$ بُعدی را تشکیل می‌دهند.

انتخاب نقطه مرکزی (Origin) و پایه‌های متعامد در این فضا برابر با تعریف هم‌ریختی در فضای $$n$$ بُعدی محسوب می‌شود. به این ترتیب می‌توان هر چیزی که در این فضا تعریف شود را در فضای اقلیدسی نیز در نظر گرفت. در نتیجه اغلب فضای اعداد حقیقی $$n$$ بُعدی را معادل با فضای اقلیدسی می‌گیرند.

آنچه باعث اختلاف بین فضای اعداد حقیقی چند بعدی و فضای اقلیدسی می‌شود، ضرورت وجود نقطه مرکز و پایه‌های متعامد است که این امر می‌تواند در فضای اقلیدسی نادیده گرفته و نقاط و مولفه‌های آن بدون در نظر گرفتن مختصات یا نقطه مرکزی بیان شود.

فصای برداری اقلیدسی

فضای برداری اقلیدسی، یک فضای اقلیدسی با بُعد متناهی است که روی اعداد حقیقی و ضرب داخلی تعریف می‌شود. بُعد فضای اقلیدسی با بًعد فضای برداری آن برابر است.

اگر $$E$$ یک فضای اقلیدسی باشد، فضای برداری متناظر با آن معمولا «فضای ترجمه» (Translation Space) نامیده و به شکل $$\overrightarrow{E}$$ نشان داده می‌شود.

عمل ترجمه بردار $$v$$ روی یک نقطه مثل $$P$$ باعث ایجاد یک نقطه به شکل $$P+v$$ می‌شود. عمل ترجمه دارای خاصیت زیر است که به آن شرکت‌پذیری گفته می‌شود.

$$\large { \displaystyle P + ( v + w ) = ( P + v ) + w }$$

مولفه‌ها و ساختار فضای اقلیدسی

بسیاری از خصوصیات فضای اقلیدسی به مولفه‌ها و ساختار آن بر می‌گردد. در این بین زیر فضا، پاره خط و اصل توازی اهمیت زیادی دارند. در ادامه به هر یک از این بخش‌ها خواهیم پرداخت.

زیر فضا

فرض کنید که $$E$$ یک فضای اقلیدسی و $$\overrightarrow{E}$$ فضای برداری متناظر با آن باشد. زیر فضا (SubSpace) هموار (Flat) این فضای اقلیدسی که با $$\overrightarrow{F}$$ نشان داده می‌شود، به صورت زیر تعریف خواهد شد.

$$\large { \displaystyle {\overrightarrow{F}} = \{{\overrightarrow{P Q}} \mid P \in F, \;Q \in F \}}$$

رابطه بالا نشانگر یک زیرفضای خطی از $$\overrightarrow{E}$$ است. به همین ترتیب زیرفضای $$F$$ یک فضای اقلیدسی با فضای برداری متناظر $$\overrightarrow{F}$$ است. زیر فضای $$\overrightarrow{F}$$ به عنوان جهت فضای $$F$$ در نظر گرفته می‌شود.

اگر $$P$$ یک نقطه از فضای $$F$$ باشد، آنگاه

$$\large  { \displaystyle F = \{ P + v \mid v \in { \overrightarrow{F} }\} }$$

از طرفی اگر $$P$$ یک نقطه از $$E$$ و $$V$$ زیرفضای برداری از $$\overrightarrow{E}$$ باشد، آنگاه رابطه زیر نشانگر یک زیرفضای اقلیدسی با جهت $$V$$ خواهد بود.

$$\large { \displaystyle P + V = \{ P + v \mid v \in V \}}$$

خط و پاره خط

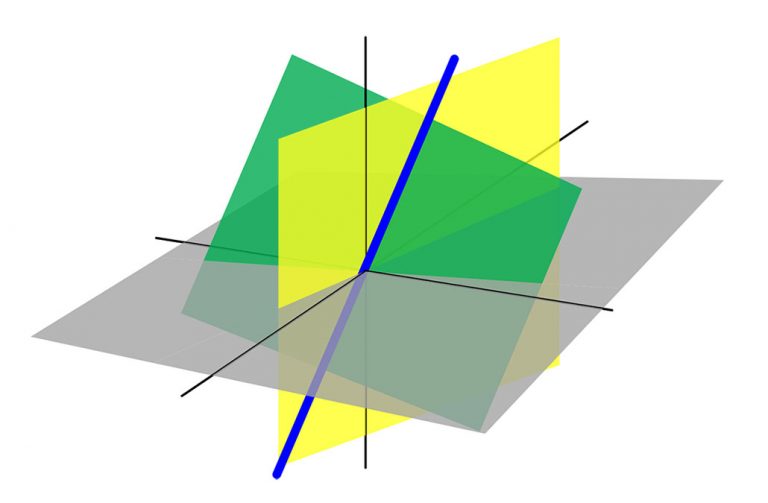
در فضای اقلیدسی، خط (Line) یک زیرفضای اقلیدسی با بُعد واحد است. از آنجایی که فضای برداری تک بُعدی با بردارهای غیر صفر پوشش داده می‌شوند، یک خط را به صورت زیر می‌توان نشان داد، بطوری که $$P$$ و $$Q$$ نقاط مجاز هستند.

$$\large { \displaystyle \{P + \lambda { \overrightarrow {P Q}} \mid \lambda \in \mathbb {R} \},}$$

این رابطه نشان می‌دهد که از بین دو نقطه، فقط یک خط راست عبور می‌کند که شامل آن دو نقطه است. به بیان دیگر هر دو خط مجزا حداکثر در یک نقطه می‌توانند اشتراک داشته باشند.

شیوه دیگری نیز برای نمایش یک خط وجود دارد. فرض کنید $$O$$ یک نقطه اختیاری (مثلا مرکز مختصات) باشد. این نقطه لزوما با $$P$$ و $$Q$$ روی یک خط راست قرار ندارد. به این ترتیب خط گذرنده از دو نقطه $$P$$ و $$Q$$ به صورت زیر معرفی می‌شود.

$$\large { \displaystyle \{ O + ( 1 - \lambda ){ \overrightarrow {OP}} + \lambda { \overrightarrow { O Q }} \mid \lambda \in \mathbb {R} \},}$$

در فضای برداری اقلیدسی، بردار صفر معمولا به وسیله $$O$$ معرفی می‌شود. در نتیجه رابطه بالا به شکل ساده‌تر نیز در خواهد آمد.

  $$\large { \displaystyle \{ ( 1 - \lambda ) P + \lambda Q \mid \lambda \in \mathbb {R} \}}$$

همچنین یک پاره خط در فضای اقلیدسی، بر اساس رابطه بالا نوشته شده و با در نظر گرفتن $$0 \leq \lambda \leq 1$$ تشکیل می‌شود. پاره خط گذرنده از دو نقطه $$P$$ و $$Q$$ را به صورت $$PQ$$ یا $$QP$$ نشان می‌دهند.

$$\large { \displaystyle PQ = QP = \{ P + \lambda { \overrightarrow {PQ}} \mid  0 \leq \lambda \leq 1 \}}$$

توازی

دو زیرفضای هم بُعد مثل $$S$$ و $$T$$، در یک فضای اقلیدسی موازی (Parallel) هستند، اگر دارای یک جهت باشند. به بیان دیگر اگر بتوان یک بردار تبدیل مثل $$v$$ پیدا کردن که $$S$$ را به $$T$$ و برعکس تبدیل کند، دو زیرفضا را موازی می‌گویند.

$$\large T = S + v$$

موضوع توازی (Parallelism) از مفاهیم پایه برای فضای اقلیدسی محسوب می‌شود. فرض کنید نقطه $$P$$ از یرفضای $$S$$ باشد. درا ین صورت فقط یک زیرفضای مثل $$P$$ وجود دارد که شامل نقطه $$P$$ بوده و با $$S$$ موازی باشد. در این صورت داریم:

$$\large T = P + \overrightarrow{S}$$

به همین علت در صفحات فضای اقلیدسی (هندسه اقلیدسی) دو خط موازی یکدیگر را در بی‌نهایت قطع می‌کنند.

ساختار متریک فضای اقلیدسی

فضای برداری $$\overrightarrow{E}$$ متناظر با فضای اقلیدسی $$E$$، یک فضای ضرب داخلی است. به این ترتیب یک «فرم متقارن دو خطی» (Symmetric Bilinear Form) دارد که «معین مثبت» (Positive Definite) است. در نتیجه روابط زیر برقرار است.

$$\large { \displaystyle { \begin{aligned}{ \overrightarrow {E}} \times { \overrightarrow {E}} & \to \mathbb {R} \\ \large (x,y) & \mapsto \langle x,y \rangle \end{aligned}}}$$

نکته: منظور از معین مثبت در اینجا به این معنی است که ضرب داخلی هر نقطه در خودش، نامنفی خواهد بود.

$$\large \forall x \neq 0 , \;\; \langle x , x \rangle >0$$

همانطور که می‌دانید در فضای اقلیدسی، به ضرب داخلی «ضرب نقطه‌ای» (Dot Product) گفته می‌شود. بخصوص زمانی که از مختصات برداری برای بیان این فضا استفاده می‌شود، ضرب داخلی دو بردار توسط ضرب نقطه‌ای مختصات نقطه‌ها مشخص خواهد شد. به همین دلیل اغلب به جای نمایش ضرب داخلی به فرم $$\langle x , y \rangle$$ از فرم $$x \cdot y$$ استفاده می‌شود. ما هم از این به بعد ضرب داخلی را به همین فرم نشان خواهیم داد.

به این ترتیب اندازه یا نرم اقلیدسی یک بردار مانند $$v$$ به شکل زیر نشان داده می‌شود.

$$\large || x || = \sqrt{x \cdot x }$$

ضرب داخلی و استفاده از اندازه بردار، این امکان را مهیا می‌سازد که از فضای متریک (Metric Space) و خصوصیات توپولوژیکی هندسه اقلیدسی استقاده کنیم.

در ادامه به بعضی از خصوصیات اصلی و پایه فضای اقلیدسی با در نظر گرفتن فضای متریک آن، خواهیم پرداخت. توجه داشته باشید که $$E$$ یک فضای اقلیدسی دلخواه و $$\overrightarrow{E}$$ فضای برداری متناظر با آن است.

فاصله و طول

فاصله یا به بیان دقیق‌تر «فاصله اقلیدسی» (Euclidean Distance) بین دو نقطه از فضای اقلیدسی مانند $$P$$ و $$Q$$ به کمک طول بردار حاصل از آن‌ها محاسبه می‌شود.

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

در نتیجه فاصله بین این دو نقطه  برابر با رابطه زیر است.

$$\large { \displaystyle d ( P , Q)= \|{ \overrightarrow {P Q}} \|}$$

به همین ترتیب طول یک پاره خط که دو سر آن نقاط $$P$$ و $$Q$$ هستند بوسیله طول بردار حاصل از این نقاط مشخص می‌شود.

طول با این مفهوم یک متر خواهد بود و در خواص آن صدق می‌کند. از جمله نامساوی مثلثی نیز برای فاصله تعریف شده برقرار است. پس برای سه نقطه از فضای اقلیدسی مانند $$P$$، $$Q$$ و $$R$$ داریم:

$$\large { \displaystyle d( P , Q ) \leq d( P , R ) + d( R , Q )}$$

نکته:واضح است که اگر نقطه $$R$$ روی خط گذرنده از $$P$$ و $$Q$$ قرار گرفته باشد، نامساوی به تساوی تبدیل خواهد شد.

تعامد و عمود بودن

دو بردار $$u$$ و $$v$$ از $$\overrightarrow{E}$$ را عمود بر هم (Perpendicular) یا متعامد (Orthogonal) گویند، اگر ضرب داخلی آن‌ها برابر با صفر باشد. بنابراین داریم:

$$\large u \cdot v = 0$$

همچنین دو زیرفضا از $$\overrightarrow{E}$$ را متعامد یا عمود بر هم گویند اگر هر بردار از اولی بر هر بردار از دومی عمود باشد. البته شرط اینکه این بردارها صفر نباشند نیز باید در نظر گرفته شود.

به همین ترتیب، دو پاره خط $$AB$$ و $$AC$$ که دارای یک نقطه مشترک (مانند $$A$$)  هستند، در فضای اقلیدسی، تشکیل یک زوایه قائمه می‌دهند اگر بردار $$\overrightarrow{AB}$$ بر بردار $$\overrightarrow{AC}$$ عمود باشد.

همچنین اگر این دوبردار بر یکدیگر عمود باشند، رابطه فیثاغورس برایشان برقرار خواهد بود. به این ترتیب برای سه نقطه $$A$$، $$B$$ و $$C$$ همچنین پاره‌خط‌های حاصل از آن‌ها داریم:

$$\large { \displaystyle |B C|^{2} = |A B|^{2} + |A C|^{2}}$$

اثبات رابطه فیثاغورس در فضای اقلیدسی بسیار ساده خواهد بود. به یاد دارید که مربع طول هر بردار را بوسیله ضرب نقطه‌ای بردار در خودش بدست می‌آوریم. به این ترتیب تساوی‌های زیر برقرار خواهند بود.

$$\large { \displaystyle { \begin{aligned}|B C |^{2} & = { \overrightarrow {B C}} \cdot { \overrightarrow {B C}} \\ \large & = \left({ \overrightarrow {B A}} + { \overrightarrow {A C}} \right) \cdot \left({ \overrightarrow {B A}} + {\overrightarrow {A C}}\right)\\ \large & = { \overrightarrow {B A}}\cdot { \overrightarrow {B A}} + { \overrightarrow {A C}} \cdot { \overrightarrow {A C}} - 2{ \overrightarrow {A B}} \cdot {\overrightarrow {A C}}\\ \large & ={ \overrightarrow {A B}}\cdot {\overrightarrow {A B}}  + { \overrightarrow {A C}} \cdot { \overrightarrow {A C}}\\ \large & = |A B|^{2} + | A C |^{2} \end{aligned}}}$$

زاویه و خصوصیات آن

زاویه (بدون در نظر گرفت جهت) بین دو بردار غیر صفر مانند $$x$$ و $$y$$ در فضای برداری $$\overrightarrow{E}$$ به صورت $$\theta$$ نمایش داده شده و به شکل زیر محاسبه می‌شود.

$$\large { \displaystyle \theta = \arccos \left( { \frac {x \cdot y}{\| x \|\| y \|}} \right)}$$

منظور از arccos، همان تابع accosine یا معکوس تابع کسینوس است.

به کمک نامساوی کوشی شوارتز (Cauchy-Schwarz Inequality) می‌توان نشان داد که پارامترهای تابع آرک کسینوس در فاصله $$[-1,1]$$ قرار می‌گیرند. در نتیجه زاویه $$\theta$$ یک عدد حقیقی و به صورت $$0 \leq \theta \leq \pi$$ برحسب رادیان یا $$0 \leq \theta \leq 180$$ برحسب درجه خواهد بود.

در صفحه اقلیدسی جهت‌دار (Oriented)، می‌توان زاویه جهت‌دار بین دو بردار را مشخص کرد. چنین زاویه‌ای بین بردار $$x$$ و $$y$$ در مقابل زاویه جهت‌دار بردارهای $$y$$ و $$x$$‌ است.

به این ترتیب هر زاویه در بازه $$\pi < \theta < 2\pi$$ برابر با زاویه منفی به صورت $$-\pi < \theta - 2\pi < 0$$ خواهد بود.

همچنین زوایه بین دو بردار با ضرب آن‌ها در یک مقدار مثبت تغییر نخواهد کرد. در حقیقت اگر $$x$$ و $$y$$ دو بردار و $$\lambda$$ و $$\mu$$ دو عدد حقیقی باشند، رابطه زیر برای زاویه بین مضاربی از این بردارها برقرار خواهد بود.

$$\large { \displaystyle \operatorname {angle} (\lambda x, \mu y) = { \begin{cases} \operatorname {angle} (x,y)\qquad \qquad {\text{if }} \lambda {  \text{ and }}\mu {\text{ have the same sign}}\\ \pi - \operatorname {angle} (x,y) \qquad { \text{otherwise}}.\end{cases}}}$$

اگر $$A$$، $$B$$ و $$C$$ سه نقطه در فضای اقلیدسی باشند، زاویه بین پاره خط‌های $$AC$$ و $$AB$$ زاویه، بین بردارهای آن‌ها است.

به همین ترتیب نیز می‌توان زاویه بین دو نیم‌خط (Half-Line) که در یک نقطه مشترک هستند را براساس زاویه بین پاره‌خط‌های حاصل از آن‌ها بدست آورد.

اگر $$\theta$$ زاویه بین دو پاره خط (Segment) باشد، بطوری که یکی روی یک خط و دیگری روی خط دیگری واقع شده باشند، آن را توسط زاویه بین دو پاره خط که از آن خط‌ها می‌گذرند، تعیین می‌کنند. زاویه بین این دو خط ممکن است $$\theta$$ یا به طور مشابه $$\pi  -  \theta$$ باشد. در این حالت به ترتیب زاویه $$\theta$$‌ در فاصله $$[0 , \pi /2 ]$$ یا $$[ \pi/2, \pi]$$ قرار خواهد گرفت.

اگر در اینجا منظور زاویه بدون جهت باشد، می‌توان محدوده زاویه بین دو خط را در بازه $$[ 0 , \pi /2 ]$$ در نظر داشت. همچنین در صفحه جهت‌دار، زاویه جهت‌دار بین دو خط در فاصله $$[-\pi/2 , \pi/2 ]$$ خواهد بود.

دستگاه مختصات دکارتی

هر فضای برداری اقلیدسی، دارای پایه‌های نرمال عمود بر هم (Orthonormal Basis) است. به این معنی که بردارهایی با اندازه واحد وجود دارند که بر هم عمود بوده و هر نقطه در این مختصات را برحسب آن‌ها می‌توان نمایش داد.

$$\large (e_1 , e_2 , \ldots , e_n ) , \;\; || e_i || = 1 , \langle e_i, e_j \rangle = 0, \;\; i \neq j$$

فضای شبه اقلیدسی

همانطور که گفته شد، فضای اقلیدسی توسط عملگر ضرب داخلی بردارها تعریف می‌شود. چنین عملگری دارای فرم معین مثبت (Positive Definite) و خطی (Bilinear) است. اگر چنین عملگری با شکل نامعین مربع که می‌تواند غیرتباهیده (non-Degenerate) باشد، یک فضای «شبیه اقلیدسی» (Pseud-Euclidean Space) ایجاد می‌کند.

به عنوان مثال، فضای مینکوفسکی که اساس «فضا-زمان» (ُSpace-Time)  تئوری نسبیت اینشتین محسوب می‌شود، یک فضای شبه اقلیدسی است. چنین فضای دارای ۴ بُعد بوده و فاصله یک نقطه از مختصات بوسیله رابطه زیر حاصل می‌شود.

$$\large x^2 + y^2 + z^2 - t^2$$

توپولوژی

به کمک فاصله اقلیدسی، می‌توان فضای اقلیدسی را به صورت یک فضای متریک در نظر گرفت. در نتیجه فضای اقلیدسی تشکیل یک توپولوژی (Topology) می‌دهد. در نتیجه، چنین توپولوژی، به نام توپولوژی اقلیدسی معروف است. زمانی که با اعداد حقیقی $$n$$-بُعدی در $$R^n$$ کار می‌کنیم، چنین توپولوژی، «توپولوژی ضربی» (Product Topology) نامیده می‌شود.

فیلم آموزش مبانی توپولوژی عمومی – جامع و کاربردی در فرادرس

کلیک کنید

مجموعه‌های باز (Open Sets) در این حالت زیرمجموعه‌هایی هستند که شامل دیسک یا «توپ‌های باز» (Open Ball) حول نقاطشان هستند. به بیان دیگر، این توپ‌های با،ز پایه‌های توپولوژی را تشکیل می‌دهند.

ابعاد توپولوژیکی یک فضای اقلیدسی برابر با بُعد فضای اقلیدسی است. به این ترتیب فضاهای اقلیدسی با ابعاد مختلف، «هم‌ریخت» (Homeomprphic) نیستند.

فضاهای اقلیدسی، «کامل» (Complete) و «بطور محلی فشرده» (Locally Compact) هستند. به این معنی که هر زیرمجموعه بسته‌ای (Closed Subset) از فضای اقلیدسی، فشرده است، اگر کران‌دار باشد. به این ترتیب تمامی دیسک‌ها یا توپ‌های بسته، فشرده هستند.

هندسه غیراقلیدسی

اگر در هندسه کلاسیک و برپایه فضای اقلیدسی، اصل و قضیه توازی را حذف کنیم، هندسه «غیراقلیدسی» یا «نااقلیدسی» (Non-Euclidean Geometries) پدید می‌آید. چنین هندسه‌ای شامل «هندسه بیضوی» (Elliptic Geometry) است که در آن مجموع زاویه‌های یک متلث بیشتر از ۱۸۰ درجه است.

از دیگر هندسه‌های نااقلیدسی می‌توان به «هندسه هذلولوی» (Hyperbolic Geometry) اشاره کرد که در آن مجموع زاویه‌های مثلث، کمتر از ۱۸۰ درجه خواهد بود.

وجود چنین هندسه‌هایی در انتهای قرن ۱۹ و ابتدای قرن ییستم، باعث ایجاد تناقضاتی در هندسه اقلیدسی شد و همین امر کمک شایانی به نظریه‌پردازی و اصل‌پردازی در هندسه و همینطور ریاضیات کرد.

کاربردهای فضای اقلیدسی

یکی از قدیمی‌ترین کاربردهای فضای اقلیدسی، نمایش و مدل‌بندی اشکال و احجام در دنیای فیزیکی بود، به همین دلیل در زمینه‌های مختلفی از علوم مانند مکانیک، نجوم و فیزیک به کار رفته است.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

از طرفی در علوم دیگر مانند ناوبری، معماری، علوم زمین و طاحی صنعتی و رباتیک نیز که با شکل‌ها و حجم‌های مختلف سروکار دارد، ردپای فضای اقلیدسی دیده می‌شود.

«فضا-مکان» (Space-Time) در «نظریه نسبت عام» (general Relatively) از یک فضای اقلیدسی گرفته نشده است. بلکه در این نظریه از «فضای منفیلد» (Manifold Space) استفاده می‌شود ولی می‌توان به صورت تقریبی از محاسبات مربوط به فضای اقلیدسی نیز در آن استفاده کرد.

در نظریه‌های جدید فیزیکی، وجود ابعاد بیشتر از طول و عرض و ارتفاع (فضای سه بُعدی) لحاظ شده است. نظریه‌های «جهان‌های موازی» (Parallel Universe) نیز در این حیطه نظریه پردازی کرده است.

جدا از هندسه اقلیدسی، فضای اقلیدسی در بسیاری از جنبه‌های ریاضیاتی نیز ظهور کرده است. فضاهای منیفلد یا خمیده (Manifold)، فضاهایی هستند که توسط فضای اقلیدسی تقریب زده می‌شوند. به این ترتیب هندسه‌های غیر اقلیدسی را می‌توان توسط خمینه‌ها و به کارگیری فضاهای اقلیدسی با ابعاد بالا، مدل‌بندی کرد. برای مثال، فضای «بیضی‌گون» (Elliptic Space) بوسیله بیضی‌ها مدل‌بندی می‌شود.

«نظریه گراف‌» (Graph Theory) به عنوان یک کاربرد از فضای اقلیدسی محسوب می‌شوند که ارتباطی با هندسه به معنی مرسوم آن ندارد و در زمینه‌های بخصوص غیر هندسی به کار گرفته می‌شود.

خلاصه و جمع‌بندی

در این نوشتار با تعریف فضای اقلیدسی و خصوصیات آن آشنا شدید. همچنین ویژگی‌های این فضا نیز مورد بحث قرار گرفت. به این ترتیب مشخص است که فضای اقلیدسی به عنوان یک زیر فضا از فضای هیلبرت (Hilbert Space) شناخته شده و در بسیاری از شاخه‌های ریاضی کاربرد دارد.

اگر این مطلب برای شما مفید بوده است، مطالب و آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش مبانی توپولوژی عمومی
• مجموعه آموزش های ریاضی و فیزیک
• مجموعه باز و بسته در ریاضیات — به زبان ساده
• فضای متریک و نامساوی مثلثی — به زبان ساده
• پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده