عمود منصف چیست؟ – به زبان ساده و با مثال

در ادامه مجموعه آموزش‌های ریاضی مجله فرادرس، در این آموزش با عمود منصف آشنا می‌شویم. علاوه بر معرفی عمود منصف، روش رسم آن را نیز بیان خواهیم کرد و قضیه‌های مربوط به آن را شرح خواهیم داد. در پایان نیز، چند مثال متنوع را حل می‌کنیم.

عمود منصف چیست ؟

«عمود منصف» (Perpendicular Bisector) خطی است که یک پاره‌خط را نصف می‌کند و بر آن عمود است.

در شکل زیر، خط RT پاره‌خط PQ را به دو بخش مساوی تقسیم کرده و بر آن عمود است. بنابراین، RT عمودمنصف پاره‌خط PQ است.

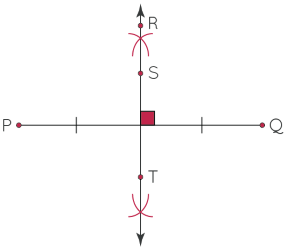
نکته: دقت کنید که از علاومت مربع ("□") بین دو زاویه برای نشان دادن قائمه بودن آن، و از تکه‌خط ("|"یا "||" یا "|||" و...) روی پاره‌خط برای نشان دادن تساوی اندازه‌ها استفاده می‌کنیم. مربع شکل زیر و دو خط "|" این موضوع را به خوبی نشان می‌دهند.

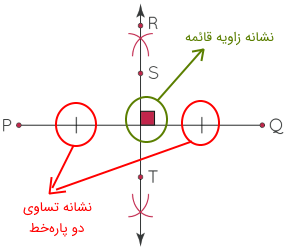
رسم عمود منصف پاره خط

برای رسم عمود منصف یک پاره‌خط، به خط‌کش و پرگار نیاز داریم. در ادامه، مراحل رسم عمود منصف یک پاره‌خط را بیان می‌کنیم.

مرحله ۱:‌ پاره‌خط AB را رسم کنید.

مرحله ۲: پرگار را به اندازه دلخواه و بیش از نصف پاره‌خط AB‌ باز کنید و از دو نقطه A و B در بالای پاره‌خط دو کمان را رسم کنید که یکدیگر را قطع کنند. همین کار را برای قسمت پایین پاره‌خط نیز انجام دهید. دقت کنید که در رسم هر چهار کمان، فاصله بین دو سر پرگار را تغییر ندهید.

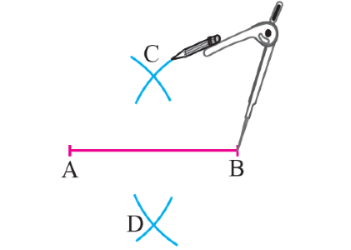
مرحله ۳: در اینجا، باید دو نقطه C و D را با خط‌کش به یکدیگر وصل کنید. خطی که از این دو نقطه عبور می‌کند، عمودمنصف AB است.

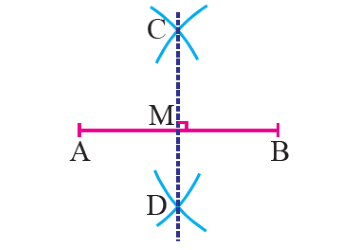
عمود منصف مثلث

با توجه به اینکه هر مثلث از سه ضلع تشکیل شده و هر کدام از این اضلاع را می‌توان به عنوان یک پاره‌خط در نظر گرفت، پس یک مثلث سه عمودمنصف دارد. در مثلث XYZ زیر، عمود منصف ضلع XY با خطی آبی رسم شده است.

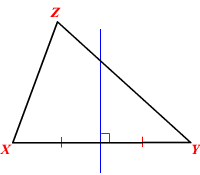
سه عمود منصف یک مثلث در یک نقطه واحد به هم می‌رسند که به آن «مرکز دایره محیطی» (Circumcenter) می‌گویند. به نقطه‌ای که سه خط یا بیشتر با هم تلاقی می‌کنند، «نقطه همرسی» (Point of Concurrency) گفته می‌شود. بنابراین، مرکز دایره محیطی، نقطه همرسی عمودمنصف‌های مثلث است. لازم به ذکر است که دایره محیطیِ مثلث، دایره‌ای است که از همه رئوس مثلث می‌گذرد.

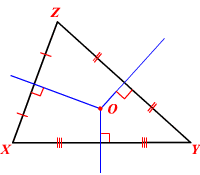
در اینجا O مرکز دایره محیطی مثلث XYZ است.

مرکز دایره محیطی، فاصله یکسانی از رئوس مثلث دارد. به عبارت دیگر، در مثلث شکل زیر، تساوی XO = YO = ZO را داریم.

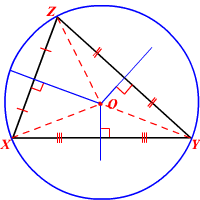
مرکز دایره محیطی برای مثلثِ حاده درون آن، برای مثلث قا‌ئم‌الزاویه روی وتر و برای مثلث منفرجه خارج از آن است.

شکل زیر، عمود منصف مثلث قائم الزاویه را نشان می‌دهد که نقطه همرسی سه عمودمنصف آن روی وتر قرار دارد.

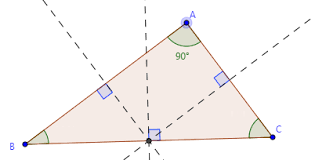
رسم عمود منصف مثلث

برای رسم عمود منصف مثلث، کافی است هریک از اضلاع را به صورت یک پاره‌خط در نظر بگیریم و عمودمنصف آن‌ها را رسم کنیم.

ابتدا، ضلع AC را در نظر بگیرید. با توجه به آنچه که پیش‌تر برای رسم عمود منصف پاره‌خط گفتیم، با استفاده از خط‌کش و پرگار، عمود منصف پاره‌خط AC را رسم می‌کنیم.

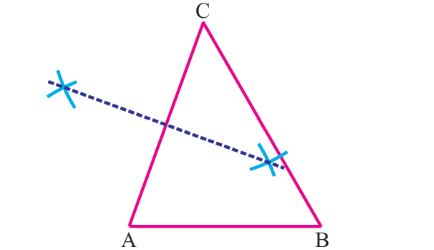
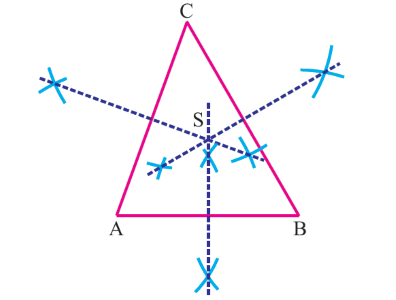
در ادامه، همین کار را برای دو ضلع دیگر انجام می‌دهیم. شکل زیر، سه عمود منصف مثلث ABC را نشان می‌دهد که در نقطه S به یکدیگر رسیده‌اند.

اثبات همرسی عمودمنصف‌های مثلث

می‌خواهیم ثابت کنیم عمود‌منصف‌های اضلاع هر مثلث همرسند. شکل زیر را در نظر بگیرید.

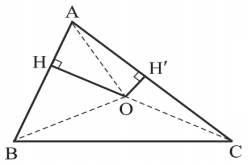
فرض کنید عمودمنصف‌های دو ضلع AB و AC یکدیگر را در نقطه O قطع کنند. با توجه به این فرض، می‌توان گفت:

• O روی عمود منصف AB است، پس OA = OB.
• O روی عمود منصف AC است، پس OA = OC.

با توجه به دو تساوی OA = OB و OA = OC، می‌توان به تساوی OB = OC رسید. از این تساوی نیز می‌توانیم چنین نتیجه بگیریم که O روی عمود منصف BC قرار دارد. بنابراین، عمود منصف BC  نیز از نقطه O می‌گذرد و در نیتجه، سه عمود منصف در یک نقطه همرسند.

عمود منصف مستطیل

عمود منصف مستطیل، خطی است که بر ضلع مستطیل عمود شده و آن را به دو قسمت مساوی تقسیم می‌کند.

بنابراین، هر مستطیل چهار عمود منصف دارد که دو تای آن‌ها روی هم می‌افتد. در شکل زیر، عمود‌منصف‌های مستطیل را می‌بینیم که در واقع چهار تا است.

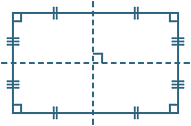
دو عمود منصف مستطیل بر هم عمود هستند. همچنین، عمودمنصف‌ها در مستطیل، محور تقارن آن نیز هستند. محل برخورد دو عمودمنصف مستطیل محل برخوردی قطرهای آن نیز هست.

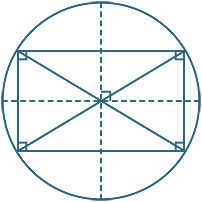
عمود منصف مستطیل نیز طبق همان روندی که برای عمود منصف پاره‌خط و مثلث بیان کردیم، رسم می‌شود. عمود منصف اشکال دیگر، مانند متوازی الاضلاع، لوزی و... نیز مانند مثلث و مستطیل و... رسم می‌شود.

قضیه عمود منصف

قضیه عمود منصف بیان می‌کند که هر نقطه روی عمود منصفِ یک پاره‌خط فاصله یکسانی از دو سر پاره‌خط دارد. شکل زیر را در نظر بگیرید که در آن، OP عمود منصف MN است.

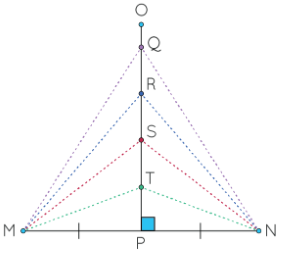
طبق قضیه عمود منصف، داریم:

MT = NT و MS = NS و MR = NR و MQ = NQ

اثبات قضیه عمود منصف

شکل زیر را در نظر بگیرید که در آن، C یک نقطه دلخواه روی عمود منصف پاره‌خط AB است که آن را در نقطه D قطع می‌کند.

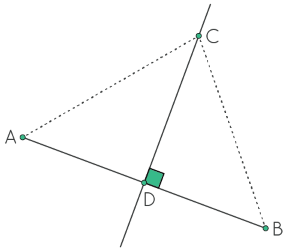
دو مثلث ACD و BCD را مقایسه می‌کنیم. داریم:

• AD = BD
• CD = CD (مشترک)
• $$∠ \text {ADC} =∠ \text{BDC} = 90 ^ \circ$$

بنابراین، می‌توانیم بگوییم که دو مثلث $$\Delta \text {ACD}$$ و $$\Delta \text{BCD}$$ با معیار دو ضلع و زاویه بین آن‌ها (ض ز ض) همنهشت هستند. بنابراین، CA = CB و این یعنی C منصف AB است.

عکس قضیه عمود منصف

همان‌طور که در شکل زیر نشان داده شده است، خط OZ پاره‌خط XY را به گونه‌ای قطع می‌کند که در آن، XZ = YZ.

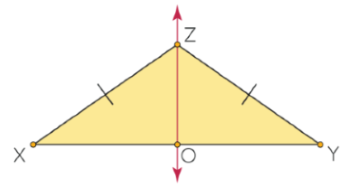
طبق عکس قضیه عمود منصف، خطی که از دو نقطه O و Z‌ عبور می‌کند، عمود منصف پاره‌خط XY است.

اثبات عکس قضیه عمود منصف

در شکل بالا فرض کنید CA = CB. باید ثابت کنیم AD = BD.

یک خط عمود از نقطه C بر پاره‌خط AB رسم کنید که آن را در نقطه D‌ قطع کند. اکنون دو مثلث $$\Delta \text{ACD}$$ و $$\Delta \text{BCD}$$ را مقایسه می‌کنیم:

• AC=BC
• CD = CD (مشترک)
• $$∠ \text {ADC} =∠ \text{BDC} = 90 ^ \circ$$

بنابراین، دو مثلث $$\Delta \text {ACD}$$ و $$\Delta \text{BCD}$$ با معیار دو ضلع و زاویه بینشان همنهشت هستند. در نتیجه، AD = BD که به این معنی است که C پاره‌خط AB را نصف کرده است.

مثال های عمود منصف

در این بخش، چند مثال را از مبحث عمودمنصف بیان می‌کنیم.

مثال اول عمود منصف

در یک هرم، پاره‌خط AD عمود منصف ضلع BC مثلث ABC‌ است. اگر AB = 20 و BD = 7 باشد، طول ضلع AC را بیابید.

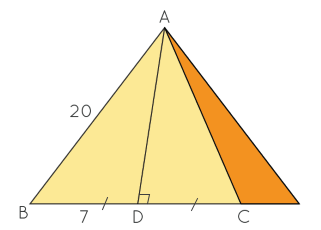
حل: همان‌طور که در صورت مسئله گفته شده، AD‌ عمود منصف BC است.

بنابراین، طبق قضیه عمود منصف، هر نقطه روی AD فاصله برابری با نقاط B و C دارد. در نتیجه، AB = AC و AC = 20.

مثال دوم عمود منصف

در هر مثلث متساوی‌الاضلاع یا متساوی‌الساقین، آیا می‌توان گفت رأس بین اضلاع روی عمود منصف قاعده است؟

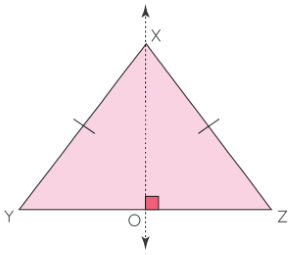
حل: از رأس X خط عمودی را بر پاره‌خط YZ رسم می‌کنیم که آن را در نقطه O قطع می‌کند. اگر XY = XZ، آنگاه طبق عکس قضیه عمود منصف، تساوی OY = OZ را داریم. رأس X روی عمود منصف قاعده YZ مثلث قرار دارد.

مثال سوم عمود منصف

در شکل زیر، خط OQ عمود منصف پاره‌خط MP است.

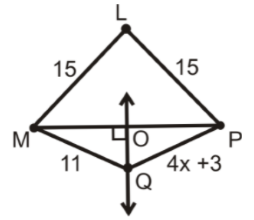
کدام پاره‌خط‌های این شکل با هم برابر هستند؟ مقدار x را محاسبه کنید. آیا نقطه L روی خط OQ قرار دارد؟

حل: طبق شکل، تساوی ML = LP و با توجه به عمود منصف بودن OQ، رابطه MO = OP را داریم. طبق قضیه مود منصف، چون Q روی عمود منصف قرار دارد، فاصله آن از دو نقطه دو سر پاره‌خط MP یکسان است و به عبارت دیگر، MQ = QP. بنابراین، می‌توان نوشت:

$$\large \begin {align*} 4 x + 3 & = 11 \\ 4 x & = 8 \\ x & = 2 \end {align*}$$

از آنجا که ML = LP، طبق عکس قضیه عمود منصف، نقطه L روی عمود منصف که OQ است، قرار دارد.

مثال چهارم عمود منصف

آیا در مثلث شکل زیر ST عمود منصف XY است؟ چرا؟

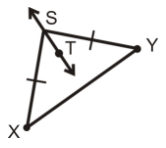
حل: تنها چیزی که از شکل بالا می‌توان برداشت کرد، این است که اندازه دو ضلع SX و SY با یکدیگر برابر است. برای عمود منصف بودن ST باید هم بر XY عمود باشد و هم آن را نصف کند. بنابراین، با توجه به اطلاعات موجود نمی‌توانیم چیزی درباره عمود منصف بودن ST‌ بگوییم.

مثال پنجم عمود منصف

اگر MO عمود منصف پاره‌خط LN باشد و LO=8، آنگاه، اندازه ON را به دست آورید.

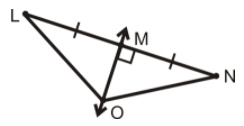
حل: طبق قضیه عمود منصف، LO = ON. بنابراین، ON = 8 خواهد بود.

مثال ششم عمود منصف

در شکل زیر، مقدار $$x$$ و طول پاره‌خط‌ها را به دست آورید.

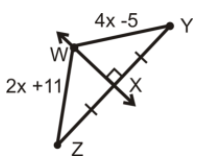
حل: همان‌گونه که در شکل مشخص شده، WX عمود منصف XZ است و طبق قضیه عمود منصف، WZ = WY. بنابراین، داریم:

$$\large \begin {align*} 2 x + 11 & = 4 x - 5 \\ 16 & = 2 x \\ 8 & = x \end {align*}$$

در نتیجه:

$$\large WZ=WY=2(8)+11=16+11=27 .$$

مثال هفتم عمود منصف

در شکل زیر مقدار $$x$$ را به دست آورید. $$m$$ عمود منصف AB است.

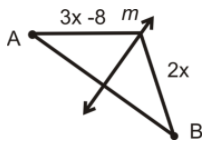
حل: طبق قضیه عمود منصف، هر دو پاره‌خط با هم برابرند. بنابراین، معادله زیر را می‌نویسیم و آن را حل می‌کنیم:

$$\large \begin {align*} 3x-8 & = 2 x \\ x & = 8 \end {align*}$$

مثال هشتم عمود منصف

در شکل زیر، مقدار $$x$$ را محاسبه کنید.

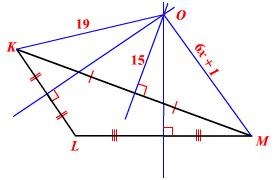
حل: همان‌طور که می‌بینیم، عمودمنصف‌های مثلث KLM رسم شده‌اند و در نقطه O به یکدیگر رسیده‌اند. طبق قضیه عمود منصف، OM = OK. بنابراین، خواهیم داشت:

$$\large \begin {align*} 6x+1 & = 19 \\ 6x & = 18 \\ x & = 3 \end {align*}$$