در آموزشهای قبلی مجله فرادرس ، با روش حذفی گاوس برای حل یک دستگاه با n n n n n n A x = b A x = b A x = b دستگاه معادلات خطی آشنا خواهیم شد. این الگوریتم تکراری، روش ژاکوبی (Jacobi method) نام دارد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
روش ژاکوبی
فرض کنید x ( 0 ) = [ x 1 ( 0 ) x 2 ( 0 ) ⋮ x n ( 0 ) ] x ^ { ( 0 ) } = \begin {bmatrix} x _ 1 ^ { ( 0 ) } \\ x _ 2 ^ { ( 0 ) } \\ \vdots \\ x _ n ^ { ( 0 ) } \end {bmatrix} x ( 0 ) = x 1 ( 0 ) x 2 ( 0 ) ⋮ x n ( 0 ) x x x n n n n n n
E ( 1 ) : a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 E ( 2 ) : a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ E ( n ) : a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = b n \large \begin {align} \quad \begin {matrix} E ( 1 ) : & a _ { 1 1 } x _ 1 & + & a _ { 1 2 } x _ 2 & + & \cdots & + & a _ { 1 n } x _ n & = & b _ 1 \\ E ( 2 ) : & a _ { 2 1 } x _ 1 & + & a _ { 2 2 } x _ 2 & + & \cdots & + & a _ { 2 n } x _ n & = & b _ 2 \\ \vdots & \vdots & & \vdots & & \ddots & & \vdots & & \vdots \\ E ( n ) : & a _ { n 1 } x _ 1 & + & a _ { n 2 } x _ 2 & + & \cdots & + & a _ { n n } x _ n & = & b _ n & \end {matrix} \end {align} E ( 1 ) : E ( 2 ) : ⋮ E ( n ) : a 11 x 1 a 21 x 1 ⋮ a n 1 x 1 + + + a 12 x 2 a 22 x 2 ⋮ a n 2 x 2 + + + ⋯ ⋯ ⋱ ⋯ + + + a 1 n x n a 2 n x n ⋮ a nn x n = = = b 1 b 2 ⋮ b n
در روش تکرار ژاکوبی، از i i i A x = b A x = b A x = b x i x _ i x i a i i ≠ 0 a_{ii} \neq 0 a ii = 0 i = 1 , 2 , . . . , n i = 1, 2, ..., n i = 1 , 2 , ... , n
x 1 = b 1 − [ a 12 x 2 + a 13 x 3 + . . . + a 1 n x n ] a 11 x 2 = b 2 − [ a 21 x 1 + a 23 x 3 + . . . + a 2 n x n ] a 22 ⋮ x n = b n − [ a n 1 x 1 + a n 2 x 2 + . . . + a n , n − 1 x n − 1 ] a n n \large \begin {align} x _ 1 = \frac { b _ 1 - \left [ a _ { 1 2 } x _ 2 + a _ { 1 3 } x _ 3 + ... + a _ { 1 n } x _ n \right ] }{ a_ { 1 1 } } \\ x _ 2 = \frac { b _ 2 - \left [ a _ { 2 1 } x _ 1 + a _ { 2 3 } x _ 3 + ... + a _ { 2 n } x _ n \right ] } { a _ { 2 2 } } \\ \quad \quad \quad \quad\quad \quad \vdots \quad \quad \quad \quad \quad \quad \\ x _ n = \frac { b _ n - \left [ a _ { n 1 } x _ 1 + a _ { n 2 } x _ 2 + ... + a _ { n , n - 1 } x _ { n - 1 } \right ] } { a _ { n n } } \end {align} x 1 = a 11 b 1 − [ a 12 x 2 + a 13 x 3 + ... + a 1 n x n ] x 2 = a 22 b 2 − [ a 21 x 1 + a 23 x 3 + ... + a 2 n x n ] ⋮ x n = a nn b n − [ a n 1 x 1 + a n 2 x 2 + ... + a n , n − 1 x n − 1 ]
اگر از نماد سیگما استفاده کنیم، برای i = 1 , 2 , . . . , n i = 1, 2, ..., n i = 1 , 2 , ... , n
x i = b i − ∑ j = 1 j ≠ i n a i j x j a i i \large \begin {align} \quad x _ i = \frac { b _ i - \sum _ { { j = 1 } _{j \neq i} } ^ { n } { a _ { i j } } x _ j} { a _ { i i } } \end {align} x i = a ii b i − ∑ j = 1 j = i n a ij x j
برای به دست آوردن تقریب اول x ( 1 ) x^{(1)} x ( 1 ) x ( 0 ) x^{(0)} x ( 0 )
x 1 ( 1 ) = b 1 − [ a 12 x 2 ( 0 ) + a 13 x 3 ( 0 ) + . . . + a 1 n x n ( 0 ) ] a 11 x 2 ( 1 ) = b 2 − [ a 21 x 1 ( 0 ) + a 23 x 3 ( 0 ) + . . . + a 2 n x n ( 0 ) ] a 22 ⋮ x n ( 1 ) = b n − [ a n 1 x 1 ( 0 ) + a n 2 x 2 ( 0 ) + . . . + a n , n − 1 x n − 1 ( 0 ) ] a n n \large \begin {align} \quad x _ 1 ^ { ( 1) } = \frac { b _ 1 - \left [ a _ { 1 2 } x _ 2 ^ { ( 0 ) } + a _ { 1 3 } x _ 3 ^ { ( 0 ) } + ... + a _ { 1 n } x _ n ^ { ( 0 ) } \right ] } { a _ { 1 1 } } \\ x _ 2 ^ { ( 1 ) } = \frac { b _ 2 - \left [ a _ { 2 1 } x _ 1 ^ { ( 0 ) } + a _ { 2 3 } x _ 3 ^ { ( 0 ) } + ... + a _{ 2 n } x _ n ^ { ( 0 ) } \right ] } { a _ { 2 2 } } \\ \quad \quad \quad \quad \quad \quad \vdots \quad \quad \quad \quad \quad \quad \\ x _ n ^ { ( 1 ) } = \frac { b _ n - \left [ a _ { n 1 } x _ 1 ^ { ( 0 ) } + a _ { n 2 } x _ 2 ^ { ( 0 ) } + ... + a _ { n , n- 1 } x _ { n - 1 } ^ { ( 0 )} \right ] } { a _ { n n } } \end {align} x 1 ( 1 ) = a 11 b 1 − [ a 12 x 2 ( 0 ) + a 13 x 3 ( 0 ) + ... + a 1 n x n ( 0 ) ] x 2 ( 1 ) = a 22 b 2 − [ a 21 x 1 ( 0 ) + a 23 x 3 ( 0 ) + ... + a 2 n x n ( 0 ) ] ⋮ x n ( 1 ) = a nn b n − [ a n 1 x 1 ( 0 ) + a n 2 x 2 ( 0 ) + ... + a n , n − 1 x n − 1 ( 0 ) ]
اگر از نماد سیگما برای i = 1 , 2 , . . . , n i = 1, 2, ..., n i = 1 , 2 , ... , n
x i ( 1 ) = b i − ∑ j = 1 j ≠ i n a i j x j ( 0 ) a i i \large \begin {align} \quad x _ i ^ { ( 1 ) } = \frac { b _ i - \sum _ { j = 1 _ { j \neq i }} ^ { n } a _ { i j } x _ j ^ { ( 0 ) } } { a _ { i i } } \end {align} x i ( 1 ) = a ii b i − ∑ j = 1 j = i n a ij x j ( 0 )
سپس، به طریق مشابه تقریب x ( 1 ) x^{(1)} x ( 1 ) x ( 2 ) x^{(2)} x ( 2 ) x x x A x = b A x = b A x = b k ≥ 1 k ≥ 1 k ≥ 1 i = 1 , 2 , . . . , n i = 1, 2, ..., n i = 1 , 2 , ... , n
x i ( k ) = b i − ∑ j = 1 j ≠ i n a i j x j ( k − 1 ) a i i \large \begin {align} \quad x _ i ^ { ( k ) } = \frac { b _ i - \sum _ { j = 1 _{ j \neq i }} ^ { n } a _ { i j } x _ j ^ { ( k - 1) } } { a _ { i i } } \end {align} x i ( k ) = a ii b i − ∑ j = 1 j = i n a ij x j ( k − 1 )
به بیان ماتریسی، دستگاه معادلات خطی زیر را در نظر بگیرید:
A x = b \large A \mathbf x = \mathbf b A x = b
که شامل n n n n n n
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] , x = [ x 1 x 2 ⋮ x n ] , b = [ b 1 b 2 ⋮ b n ] . \large A = \begin {bmatrix} a _ { 1 1 } & a _ { 1 2 } & \cdots & a _ { 1 n } \\ a _ { 2 1 } & a _ { 2 2 } & \cdots & a _ { 2 n } \\ \vdots & \vdots & \ddots & \vdots \\a _ { n 1 } & a _ { n 2 } & \cdots & a _ { n n } \end {bmatrix}, \qquad \mathbf { x } = \begin {bmatrix} x _ { 1 } \\ x _ 2 \\ \vdots \\ x _ n \end {bmatrix} , \qquad \mathbf {b } = \begin {bmatrix} b _ { 1 } \\ b _ 2 \\ \vdots \\ b _ n \end {bmatrix} . A = a 11 a 21 ⋮ a n 1 a 12 a 22 ⋮ a n 2 ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ⋮ a nn , x = x 1 x 2 ⋮ x n , b = b 1 b 2 ⋮ b n .
ماتریس A A A ماتریس قطری D D D R R R A = D + R A = D + R A = D + R
D = [ a 11 0 ⋯ 0 0 a 22 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ a n n ] , R = [ 0 a 12 ⋯ a 1 n a 21 0 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ 0 ] . \large D = \begin {bmatrix} a _ { 1 1 } & 0 & \cdots & 0 \\ 0 & a _ { 2 2 } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\0 & 0 & \cdots & a _ { n n } \end {bmatrix} \text{, } \;\;\;\; R = \begin {bmatrix} 0 & a _ { 1 2 } & \cdots & a _ { 1 n } \\ a _ { 2 1 } & 0 & \cdots & a _ { 2 n } \\ \vdots & \vdots & \ddots & \vdots \\ a _ { n 1 } & a _ { n 2 } & \cdots & 0 \end {bmatrix} . D = a 11 0 ⋮ 0 0 a 22 ⋮ 0 ⋯ ⋯ ⋱ ⋯ 0 0 ⋮ a nn , R = 0 a 21 ⋮ a n 1 a 12 0 ⋮ a n 2 ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ⋮ 0 .
در نتیجه، جواب تکراری با معادله زیر به دست میآید:
x ( k + 1 ) = D − 1 ( b − R x ( k ) ) \large \mathbf { x } ^ { ( k + 1 ) } = D ^ { - 1 } ( \mathbf { b } - R \mathbf { x } ^ { ( k ) } ) x ( k + 1 ) = D − 1 ( b − R x ( k ) )
که در آن، x ( k ) \mathbf{x}^{(k)} x ( k ) k k k x \mathbf{x} x x ( k + 1 ) \mathbf{x}^{(k+1)} x ( k + 1 ) k + 1 k + 1 k + 1
همگرایی روش ژاکوبی
شرط همگرایی استاندارد (برای هر روش تکراری) وقتی تحقق مییابد که شعاع طیفی ماتریس تکرار کمتر از ۱ باشد:
ρ ( D − 1 R ) < 1. \large \rho ( D ^ { - 1 } R ) < 1 . ρ ( D − 1 R ) < 1.
شعاع طیفی: اگر λ 1 \lambda _ 1 λ 1 λ n \lambda _ n λ n A A A ρ ( A ) \rho (A) \! ρ ( A )
ρ ( A ) = max i ( ∣ λ i ∣ ) \large \rho(A) = \max_i(|\lambda_i|) \! ρ ( A ) = i max ( ∣ λ i ∣ )
یک شرط لازم (و نه کافی) برای همگرایی این روش، این است که ماتریس A A A
∣ a i i ∣ > ∑ j ≠ i ∣ a i j ∣ . \large \left | a _ { i i } \right | > \sum _ { j \ne i } { \left | a _ { i j } \right | } . ∣ a ii ∣ > j = i ∑ a ij .
البته حتی اگر این شرایط نیز برقرار نباشد، گاهی روش ژاکوبی همگرا خواهد شد.
لازم به ذکر است که روش ژاکوبی برای هر ماتریس مثبت معین متقارن همگرا نیست. برای مثال:
A = ( 29 2 1 2 6 1 1 1 1 5 ) ⇒ D − 1 R = ( 0 2 29 1 29 1 3 0 1 6 5 5 0 ) ⇒ ρ ( D − 1 R ) ≈ 1.0661 . \large A = \begin {pmatrix} 2 9 & 2 & 1 \\ 2 & 6 & 1 \\ 1 & 1 & \frac { 1 } { 5 } \end {pmatrix} \quad \Rightarrow \quad D ^ { - 1 } R = \begin {pmatrix} 0 & \frac { 2 } { 2 9 } & \frac { 1 } { 2 9 } \\ \frac { 1 } { 3 } & 0 & \frac { 1 } { 6 } \\ 5 & 5 & 0 \end {pmatrix} \quad \Rightarrow \quad \rho ( D ^ { - 1 } R ) \approx 1 . 0 6 6 1 \, . A = 29 2 1 2 6 1 1 1 5 1 ⇒ D − 1 R = 0 3 1 5 29 2 0 5 29 1 6 1 0 ⇒ ρ ( D − 1 R ) ≈ 1.0661 .
مثالهایی از روش ژاکوبی
در این بخش، چند مثال را بررسی میکنیم.
مثال ۱
جواب دستگاه سه معادله و سه مجهول زیر را با استفاده از روش ژاکوبی بیابید:
E ( 1 ) : 3 x 1 + x 2 + 4 x 3 = 1 E ( 2 ) : x 1 + 5 x 2 + 9 x 3 = 1 E ( 3 ) : 2 x 1 + 6 x 2 + 5 x 3 = 1 \large \begin {align} \quad \begin {matrix} E ( 1 ) : & 3 x _ 1 & + & x _ 2 & + & 4 x _ 3 & = & 1 \\ E ( 2 ) : & x _ 1 & + & 5 x _ 2 & + & 9 x _ 3 & = & 1 \\ E ( 3 ) : & 2 x _ 1 & + & 6 x _ 2 & + & 5 x _ 3 & = & 1 \end {matrix} \end {align} E ( 1 ) : E ( 2 ) : E ( 3 ) : 3 x 1 x 1 2 x 1 + + + x 2 5 x 2 6 x 2 + + + 4 x 3 9 x 3 5 x 3 = = = 1 1 1
حل: تقریب اولیه x ( 0 ) = [ 0.22 0.03 0.06 ] x ^ { ( 0 ) } = \begin {bmatrix} 0 . 2 2 \\ 0 . 0 3 \\ 0 . 0 6 \end {bmatrix} x ( 0 ) = 0.22 0.03 0.06 x i x _ i x i i = 1 , 2 , 3 i = 1 , 2 , 3 i = 1 , 2 , 3
x 1 = 1 − x 2 − 4 x 3 3 x 2 = 1 − x 1 − 9 x 3 5 x 3 = 1 − 2 x 1 − 6 x 2 5 \large \begin {align} \quad x _ 1 = \frac { 1 - x _ 2 - 4 x _ 3 } { 3 } \\ \quad x _ 2 = \frac { 1 - x _ 1 - 9 x _ 3 } { 5 } \\ \quad x _ 3 = \frac { 1 - 2 x _ 1 - 6 x _ 2 } { 5} \end {align} x 1 = 3 1 − x 2 − 4 x 3 x 2 = 5 1 − x 1 − 9 x 3 x 3 = 5 1 − 2 x 1 − 6 x 2
تقریب نخست x ( 1 ) x^{(1)} x ( 1 )
x 1 ( 1 ) = 1 − ( 0.03 ) − 4 ( 0.06 ) 3 = 0.243 x 2 ( 1 ) = 1 − ( 0.22 ) − 9 ( 0.06 ) 5 = 0.048 x 3 ( 1 ) = 1 − 2 ( 0.22 ) − 6 ( 0.03 ) 5 = 0.076 \large \begin {align} \quad x _ 1 ^ { ( 1 ) } = \frac { 1 - ( 0 . 0 3 ) - 4 ( 0 . 0 6 ) } { 3 } = 0 . 2 4 3 \\ \quad x _ 2 ^ { ( 1 ) } = \frac { 1 - ( 0 . 2 2 ) - 9 ( 0 .0 6 ) } { 5 } = 0 . 0 4 8 \\ \quad x _ 3 ^ { ( 1 ) } = \frac { 1 - 2 ( 0 . 2 2 ) - 6 ( 0 . 0 3 ) } { 5 } = 0 . 076 \end {align} x 1 ( 1 ) = 3 1 − ( 0.03 ) − 4 ( 0.06 ) = 0.243 x 2 ( 1 ) = 5 1 − ( 0.22 ) − 9 ( 0.06 ) = 0.048 x 3 ( 1 ) = 5 1 − 2 ( 0.22 ) − 6 ( 0.03 ) = 0.076
اگر همینگونه مراحل را ادامه دهیم، به تقریبهای مناسبی خواهیم رسید. جواب واقعی این دستگاه x = [ 0.2 3 ˉ 0.0 3 ˉ 0.0 6 ˉ ] x = \begin {bmatrix} 0 . 2 \bar { 3 } \\ 0 . 0 \bar { 3 } \\ 0 . 0 \bar { 6 } \end {bmatrix} x = 0.2 3 ˉ 0.0 3 ˉ 0.0 6 ˉ
مثال 2
دستگاه معادلات خطی A x = b A x = b A x = b x ( 0 ) x ^ (0) x ( 0 )
A = [ 2 1 5 7 ] , b = [ 11 13 ] , x ( 0 ) = [ 1 1 ] . \large A = \begin {bmatrix} 2 & 1 \\ 5 & 7 \\ \end {bmatrix}, \ b = \begin {bmatrix} 1 1 \\ 1 3 \\ \end {bmatrix} \ \text {,} \quad x ^ { ( 0 ) } = \begin {bmatrix} 1 \\ 1 \\ \end {bmatrix} . A = [ 2 5 1 7 ] , b = [ 11 13 ] , x ( 0 ) = [ 1 1 ] .
از معادله x ( k + 1 ) = D − 1 ( b − R x ( k ) ) x ^ { ( k + 1 ) } = D ^ {- 1 } ( b - R x ^ { ( k ) } ) x ( k + 1 ) = D − 1 ( b − R x ( k ) ) x x x D − 1 ( b − R x ( k ) ) = T x ( k ) + C D ^ { - 1 } ( b - R x ^ {( k ) } ) = T x ^ { ( k ) } + C D − 1 ( b − R x ( k ) ) = T x ( k ) + C T = − D − 1 R T=-D^{-1}R T = − D − 1 R C = D − 1 b C = D ^ {-1} b C = D − 1 b R = L + U R = L + U R = L + U L L L U U U A A A
D − 1 = [ 1 / 2 0 0 1 / 7 ] , L = [ 0 0 5 0 ] , U = [ 0 1 0 0 ] . \large D ^ { - 1 } = \begin {bmatrix} 1 / 2 & 0 \\ 0 & 1 / 7 \\ \end {bmatrix} , \ L = \begin {bmatrix} 0 & 0 \\ 5 & 0 \\ \end {bmatrix} , \quad U = \begin {bmatrix} 0 & 1 \\ 0 & 0 \\ \end {bmatrix} . D − 1 = [ 1/2 0 0 1/7 ] , L = [ 0 5 0 0 ] , U = [ 0 0 1 0 ] .
ماتریس T = − D − 1 ( L + U ) T = - D ^ {-1} ( L + U ) T = − D − 1 ( L + U )
T = [ 1 / 2 0 0 1 / 7 ] { [ 0 0 − 5 0 ] + [ 0 − 1 0 0 ] } = [ 0 − 1 / 2 − 5 / 7 0 ] . \large T = \begin {bmatrix} 1 / 2 & 0 \\ 0 & 1 / 7 \\ \end {bmatrix} \left \{ \begin {bmatrix} 0 & 0 \\ - 5 & 0 \\ \end {bmatrix} + \begin {bmatrix} 0 & - 1 \\ 0 & 0 \\ \end {bmatrix} \right \} = \begin {bmatrix} 0 & - 1 / 2 \\ - 5 / 7 & 0 \\ \end {bmatrix} . T = [ 1/2 0 0 1/7 ] { [ 0 − 5 0 0 ] + [ 0 0 − 1 0 ] } = [ 0 − 5/7 − 1/2 0 ] .
برای C C C
C = [ 1 / 2 0 0 1 / 7 ] [ 11 13 ] = [ 11 / 2 13 / 7 ] . \large C = \begin {bmatrix} 1 / 2 & 0 \\ 0 & 1 / 7 \\ \end {bmatrix} \begin {bmatrix} 1 1 \\ 1 3 \\ \end {bmatrix} = \begin {bmatrix} 1 1 / 2 \\ 1 3 / 7 \\ \end {bmatrix} . C = [ 1/2 0 0 1/7 ] [ 11 13 ] = [ 11/2 13/7 ] .
اکنون، با داشتن مقادیرِ محاسبه شده T T T C C C x x x x ( 1 ) = T x ( 0 ) + C x ^ {(1)} = T x ^ { ( 0 ) } + C x ( 1 ) = T x ( 0 ) + C
x ( 1 ) = [ 0 − 1 / 2 − 5 / 7 0 ] [ 1 1 ] + [ 11 / 2 13 / 7 ] = [ 5.0 8 / 7 ] ≈ [ 5 1.143 ] . \large x ^ { ( 1 ) } = \begin {bmatrix} 0 & - 1 / 2 \\ - 5 / 7 & 0 \\ \end {bmatrix} \begin {bmatrix} 1 \\ 1 \\ \end{bmatrix} + \begin {bmatrix} 1 1 / 2 \\ 1 3 / 7 \\ \end {bmatrix} = \begin {bmatrix} 5 . 0 \\ 8 / 7 \\ \end {bmatrix} \approx \begin {bmatrix} 5 \\ 1 . 1 4 3 \\ \end {bmatrix} . x ( 1 ) = [ 0 − 5/7 − 1/2 0 ] [ 1 1 ] + [ 11/2 13/7 ] = [ 5.0 8/7 ] ≈ [ 5 1.143 ] .
نتیجه تکرار بعدی نیز به صورت زیر است:
x ( 2 ) = [ 0 − 1 / 2 − 5 / 7 0 ] [ 5.0 8 / 7 ] + [ 11 / 2 13 / 7 ] = [ 69 / 14 − 12 / 7 ] ≈ [ 4.929 − 1.714 ] . \large x ^ { ( 2 ) } = \begin {bmatrix} 0 & - 1 / 2 \\ - 5 / 7 & 0 \\ \end {bmatrix} \begin {bmatrix} 5 . 0 \\ 8 / 7 \\ \end {bmatrix} + \begin {bmatrix} 1 1 / 2 \\ 1 3 / 7 \\ \end {bmatrix} = \begin {bmatrix} 6 9 / 1 4 \\ - 1 2 / 7 \\ \end {bmatrix} \approx \begin {bmatrix} 4 . 9 2 9 \\ - 1 . 7 1 4 \\ \end {bmatrix} . x ( 2 ) = [ 0 − 5/7 − 1/2 0 ] [ 5.0 8/7 ] + [ 11/2 13/7 ] = [ 69/14 − 12/7 ] ≈ [ 4.929 − 1.714 ] .
این روال را تا جایی ادامه میدهیم که شرط همگرایی ∥ A x ( n ) − b ∥ \|Ax^{(n)} - b\| ∥ A x ( n ) − b ∥
x = [ 7.111 − 3.222 ] . \large x = \begin {bmatrix} 7 . 1 1 1 \\ - 3 . 2 2 2 \end {bmatrix} . x = [ 7.111 − 3.222 ] .
مثال ۳
سیستم زیر را در نظر بگیرید:
10 x 1 − x 2 + 2 x 3 = 6 , − x 1 + 11 x 2 − x 3 + 3 x 4 = 25 , 2 x 1 − x 2 + 10 x 3 − x 4 = − 11 , 3 x 2 − x 3 + 8 x 4 = 15. \large \begin {align} 1 0 x _ 1 - x _ 2 + 2 x _ 3 & = 6 , \\ - x _ 1 + 1 1 x _ 2 - x _ 3 + 3 x _ 4 & = 2 5 , \\ 2 x _ 1 - x _ 2 + 1 0 x _ 3 - x _ 4 & = - 1 1 , \\ 3 x _ 2 - x _ 3 + 8 x _ 4 & = 1 5 . \end {align} 10 x 1 − x 2 + 2 x 3 − x 1 + 11 x 2 − x 3 + 3 x 4 2 x 1 − x 2 + 10 x 3 − x 4 3 x 2 − x 3 + 8 x 4 = 6 , = 25 , = − 11 , = 15.
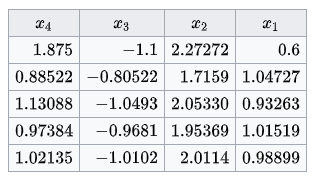
اگر تقریب اولیه ( 0 , 0 , 0 , 0 ) (0,0,0,0) ( 0 , 0 , 0 , 0 )
x 1 = ( 6 + 0 − ( 2 ∗ 0 ) ) / 10 = 0.6 , x 2 = ( 25 + 0 + 0 − ( 3 ∗ 0 ) ) / 11 = 25 / 11 = 2.2727 , x 3 = ( − 11 − ( 2 ∗ 0 ) + 0 + 0 ) / 10 = − 1.1 , x 4 = ( 15 − ( 3 ∗ 0 ) + 0 ) / 8 = 1.875. \large \begin {align} x _ 1 & = ( 6 + 0 - ( 2 * 0 ) ) / 1 0 = 0 . 6 , \\ x _ 2 & = ( 2 5 + 0 + 0 - ( 3 * 0 ) ) / 1 1 = 2 5 / 1 1 = 2 . 2 7 2 7 , \\ x _ 3 & = ( - 1 1 - ( 2 * 0 ) + 0 + 0 ) / 1 0 = - 1 . 1 , \\ x _ 4 & = ( 1 5 - ( 3 * 0 ) + 0 ) / 8 = 1 . 8 7 5 . \end {align} x 1 x 2 x 3 x 4 = ( 6 + 0 − ( 2 ∗ 0 )) /10 = 0.6 , = ( 25 + 0 + 0 − ( 3 ∗ 0 )) /11 = 25/11 = 2.2727 , = ( − 11 − ( 2 ∗ 0 ) + 0 + 0 ) /10 = − 1.1 , = ( 15 − ( 3 ∗ 0 ) + 0 ) /8 = 1.875.
جوابهای مربوط به ۵ تکرار در جدول زیر آورده شده است:
برنامه پایتون روش ژاکوبی برای این مثال به صورت زیر است:
اگر برنامه بالا را اجرا کنیم، خواهیم داشت:
System:
10.0*x1 + -1.0*x2 + 2.0*x3 + 0.0*x4 = 6.0
-1.0*x1 + 11.0*x2 + -1.0*x3 + 3.0*x4 = 25.0
2.0*x1 + -1.0*x2 + 10.0*x3 + -1.0*x4 = -11.0
0.0*x1 + 3.0*x2 + -1.0*x3 + 8.0*x4 = 15.0
Current solution: [ 0. 0. 0. 0.]
Current solution: [ 0.6 2.27272727 -1.1 1.875 ]
Current solution: [ 1.04727273 1.71590909 -0.80522727 0.88522727]
Current solution: [ 0.93263636 2.05330579 -1.04934091 1.13088068]
Current solution: [ 1.01519876 1.95369576 -0.96810863 0.97384272]
Current solution: [ 0.9889913 2.01141473 -1.0102859 1.02135051]
Current solution: [ 1.00319865 1.99224126 -0.99452174 0.99443374]
Current solution: [ 0.99812847 2.00230688 -1.00197223 1.00359431]
Current solution: [ 1.00062513 1.9986703 -0.99903558 0.99888839]
Current solution: [ 0.99967415 2.00044767 -1.00036916 1.00061919]
Current solution: [ 1.0001186 1.99976795 -0.99982814 0.99978598]
Current solution: [ 0.99994242 2.00008477 -1.00006833 1.0001085 ]
Current solution: [ 1.00002214 1.99995896 -0.99996916 0.99995967]
Current solution: [ 0.99998973 2.00001582 -1.00001257 1.00001924]
Current solution: [ 1.00000409 1.99999268 -0.99999444 0.9999925 ]
Current solution: [ 0.99999816 2.00000292 -1.0000023 1.00000344]
Current solution: [ 1.00000075 1.99999868 -0.99999899 0.99999862]
Current solution: [ 0.99999967 2.00000054 -1.00000042 1.00000062]
Current solution: [ 1.00000014 1.99999976 -0.99999982 0.99999975]
Current solution: [ 0.99999994 2.0000001 -1.00000008 1.00000011]
Current solution: [ 1.00000003 1.99999996 -0.99999997 0.99999995]
Current solution: [ 0.99999999 2.00000002 -1.00000001 1.00000002]
Current solution: [ 1. 1.99999999 -0.99999999 0.99999999]
Current solution: [ 1. 2. -1. 1.]
Solution:
[ 1. 2. -1. 1.]
Error:
[ -2.81440107e-08 5.15706873e-08 -3.63466359e-08 4.17092547e-08]
پیادهسازی روش ژاکوبی در متلب
برنامه روش ژاکوبی در متلب به صورت زیر است (توضیحات مربوط به ورودیها و خروجیها در برنامه ذکر شده است):
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^
فیلم های آموزش روش ژاکوبی – به زبان ساده (+ دانلود فیلم آموزش رایگان) فیلم آموزشی روش ژاکوبی فیلم آموزشی همگرایی روش ژاکوبی فیلم آموزشی حل چند مثال از روش ژاکوبی فیلم آموزشی پیادهسازی روش ژاکوبی در متلب 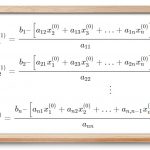














مرسی عالی بود
تشکر استاد عالی بود.
فیلم ژاکوبی تو متلب خیلیییییی خوب بود ????استادای فردوسی ینی انقدر بدردبخور درس نمیدن ✋?
واقعا متشکرم کلیپ های آموزشی شما واقعا عالی هستند و بسیار مشتاقم که زود تر بخش هایی که هنوز فاقد کلیپ میباشند مانند روش گوس سایدل زود تر از این امکان بهره مند شوند