راس زاویه چیست؟ – به زبان ساده + حل مثال تصویری
راس زاویه نقطه مشترک ضلعهای زاویه است. زاویهها، از دو ضلع و یک راس تشکیل میشوند. به عنوان مثال، سطح یک کتاب را در نظر بگیرید. هر دو لبه سطح کتاب، در یک نقطه به هم برخورد میکنند. این نقطه، همان رأس زاویه است. در این مقاله، مفهوم راس زاویه در شکلهای مختلف هندسی و نحوه نامگذاری آن را به همراه حل چند مثال تصویری آموزش میدهیم.
زاویه چیست و چه اجزایی دارد؟
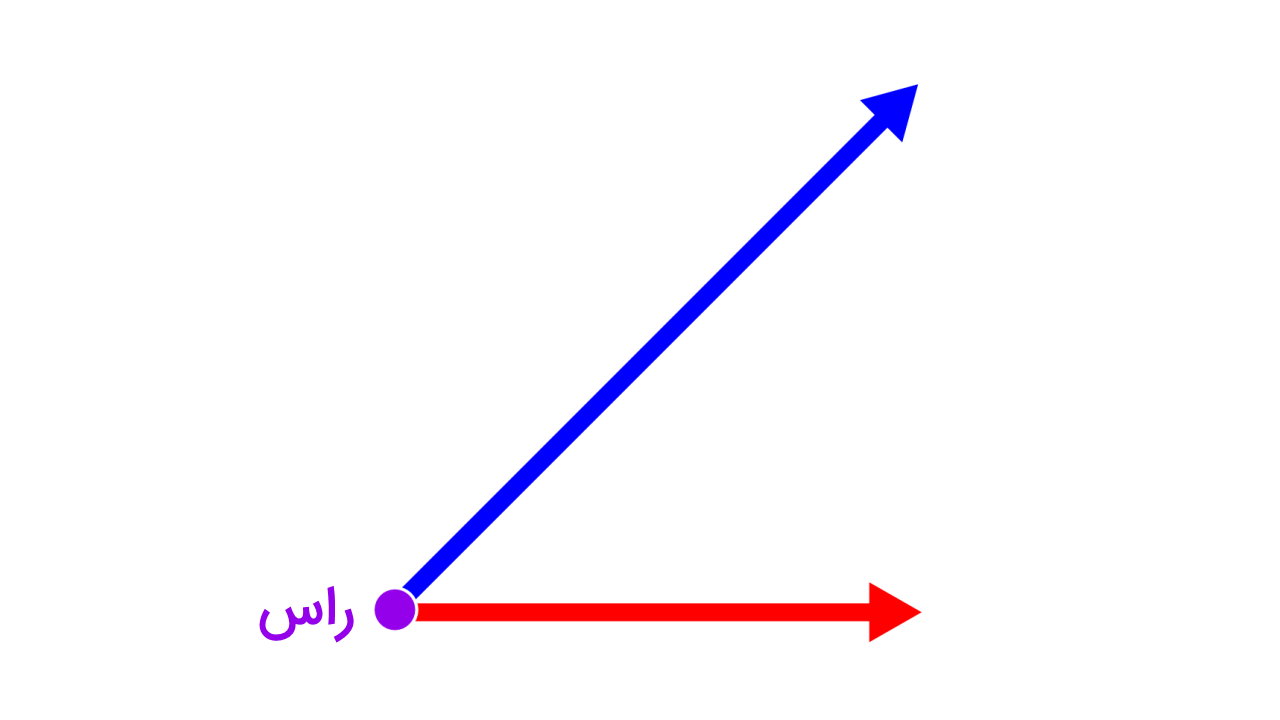
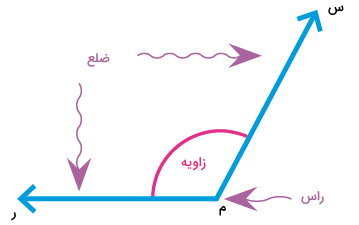
به شکلهایی که از دو ضلع و یک راس تشکیل میشوند، زاویه میگویند. ضلعهای زاویه میتوانند از نوع خط، نیمخط یا پارهخط باشند. اندازه زاویه، میزان اندازه بازشدگی بین ضلعهای آن است. تصویر زیر، اجزای مختلف یک زاویه را نمایش میدهد. این زاویه، از اتصال دو نیمخط تشکیل شده است.
مطالب مرتبط با این مبحث:
راس زاویه چیست؟
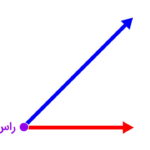
به نقطه شروع ضلعهای یک زاویه یا به محل برخورد ضلعهای یک زاویه، «راس» (Vertex) میگویند.
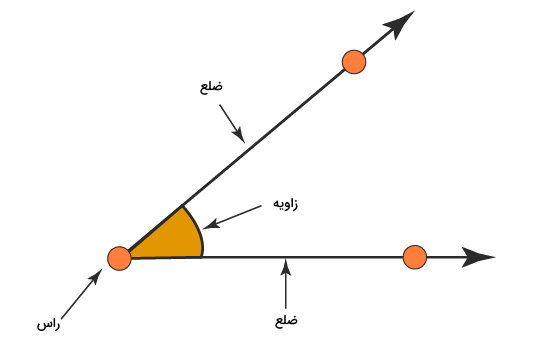
در واقع، نقطه اشتراک دو خط، نیمخط یا پارهخط، راس زاویه ایجاد شده در محل برخورد آنها است. نیمخط «م ر» را در نظر بگیرید.

اگر این نیمخط را حول نقطه ابتدایی آن (نقطه م)، دوران دهیم، موقعیت آن نسبت به محل اولیه تغییر میکند. در موقعیت ثانویه، نام نیمخط را به «م س» تغییر میدهیم.
اکنون، یک زاویه داریم. اندازه این زاویه، برابر با میزان جابجایی نیمخط اولیه نسبت به نیمخط ثانویه است. این دو نیمخط، ضلعهای زاویه را تشکیل میدهند. نقطهای که نیمخط حول آن دوران کرد نیز با عنوان راس زاویه شناخته میشود.
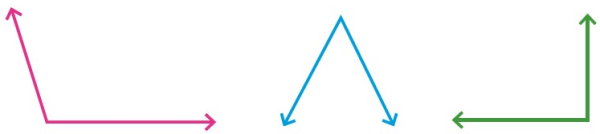
مثال ۱: تعیین راس زاویه ها
در تصویر زیر، چند زاویه نمایش داده شدهاند. راسهای این زاویهها را با فلش مشخص کنید.
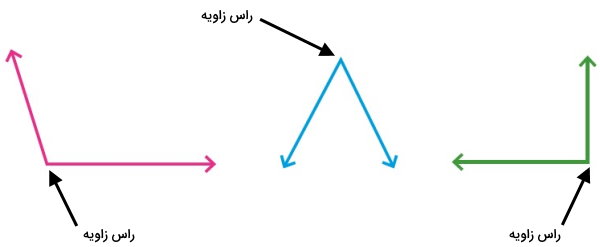
راس زاویههای بالا، محلی است که دو ضلع با هم برخورد میکنند (نقطه شروع ضلعها). بنابراین، راسهای زاویههای بالا را به صورت زیر نمایش میدهیم.
نامگذاری راس زاویه چگونه است؟
ضلعها و راسهای یک زاویه معمولا با استفاده از حروف (فارسی یا انگلیسی) نامگذاری میشوند. به عنوان مثال، تصویر زیر، زاویهای متشکل از دو نیمخط را نمایش میدهد. یکی از نیمخطها را با حرف «الف» و نیمخط دیگر را با حرف «ب» مشخص میکنیم.
محل برخورد دو نیمخط (راس زاویه) نیز باید دارای نام باشد. حرف «ج» را در کنار راس مینویسیم.
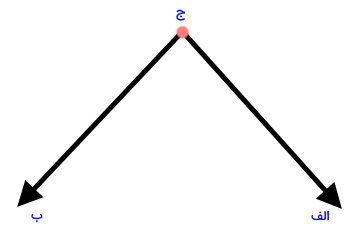
نام راس زاویه بالا، به صورت راس «ج» بیان میشود. نحوه بیان نام ضلعهای زاویه نیز به صورت ضلع «ج الف» و ضلع «ج ب» است. توجه داشته باشید که این نامها، با حرف معرف رأس زاویه شروع شدهاند. نامگذاری اجزای زاویهها به صورت دلخواه انجام میگیرد اما نحوه بیان آنها، قواعد خاص خود را دارد. به عنوان مثال، به زاویه بالا، زاویه «الف ج ب» میگوئیم. حرف معرف راس، همیشه در وسط دو حرف معرف ضلع قرار میگیرد.
مثال ۲: نامگذاری زاویه
زاویههای نمایش داده شده در مثال ۱ را نامگذاری کنید. نام راس هر زاویه چیست؟
به منظور نامگذاری هر راس، از انتهای یک ضلع شروع میکنیم و به ترتیب به انتهای ضلع اول، راس و انتهای ضلع دوم، یک حرف را اختصاص میدهیم.
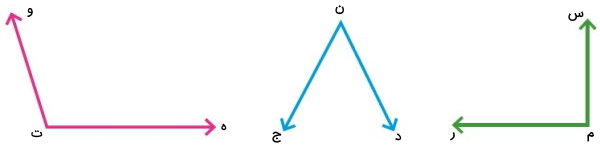
اینکه برای هر نقطه، چه حرفی را انتخاب کنیم، اهمیت چندانی ندارد. نکته مهم، نحوه بیان نام زاویه است. زاویههای بالا عبارت هستند از:
- زاویه سبز: زاویه «س م ر»
- زاویه آبی: زاویه «د ن ج»
- زاویه قرمز: زاویه «ه ت و»
به این ترتیب، نام راس هر زاویه نیز به صورت زیر نوشته میشود:
- راس زاویه سبز: راس «م»
- راس زاویه آبی: راس «م»
- راس زاویه قرمز: راس «م»
راس زاویه در چند ضلعی ها
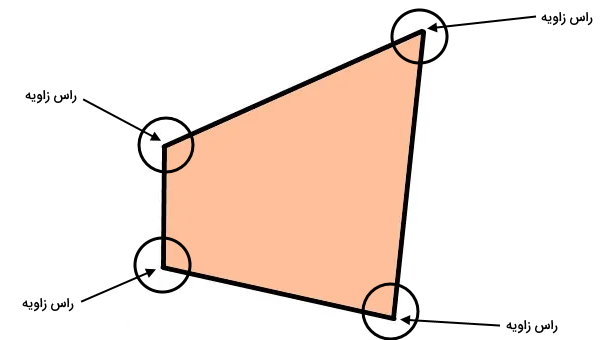
یکی از اجزای مهم شکلهای چندضلعی، رأس زاویههای داخلی آنها است. در چندضلعیها، از برخورد دو ضلع، یک زاویه داخلی ایجاد میشود. ضلعهای این زاویه، همدیگر را در نقطهای به نام راس یا گوشه قطع میکنند.
تصویر زیر، زاویههای موجود در یک چندضلعی را نمایش میدهد. راس هر یک از زاویهها را با فلش مشخص کردهایم.
مثال ۳: تعیین زاویه های چندضلعی
چندضلعی زیر را در نظر بگیرید.
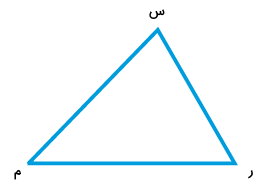
با توجه به شکل، به سوالات زیر پاسخ دهید:
- زاویههای موجود در چندضلعی چه هستند؟
- چندضلعی، چند راس دارد؟
- نام هر یک از راسهای چندضلعی چیست؟
محل برخورد هر دو ضلع، یک زاویه را تشکیل میدهد. ضلعهای شکل بالا عبارت هستند از:
- ضلع «ر س»
- ضلع «س م»
- ضلع «م ر»
از اینرو، زاویههای زیر را میتوان در شکل پیدا کرد:
- زاویه «ر س م»: زاویه حاصل از ضلعهای «ر س» و «س م»
- زاویه «س م ر»: زاویه حاصل از ضلعهای «س م» و «م ر»
- زاویه «م ر س»: زاویه حاصل از ضلعهای «م ر» و «ر س»
بنابراین، چندضلعی «س م ر»، سه زاویه دارد. راسهای هر یک از این زاویهها عبارت هستند از:
- راس «س»: راس زاویه «ر س م»
- راس «م»: راس زاویه «س م ر»
- راس «ر»: راس زاویه «م ر س»
رابطه بین قطر و راس زاویه
راس زاویه چندضلعیها، در تعریف و ترسیم قطرهای آنها نیز کاربرد دارد. قطر چندضلعی، پارهخطی است که راسهای غیر مجاور آن را به یکدیگر متصل میکند. تصویر زیر، قطرهای یک پنجضلعی را نمایش میدهد.

تعداد قطرهای چندضلعیها، به تعداد راسهای زاویه بستگی دارد. فرمول تعداد قطر چندضلعی به صورت زیر نوشته میشود:
- dn: تعداد قطرهای چندضلعی
- n: تعداد راسهای چندضلعی
مثال ۴: محاسبه تعداد قطرهای چند ضلعی
تعداد قطرهای یک هشتضلعی را حساب کنید.
در چندضلعیها، تعداد قطرها و راسها برابر هستند. به عبارت دیگر، یک هشتضلعی، هشت رأس دارد. به این ترتیب، برای محاسبه تعداد قطرها، از فرمول زیر استفاده میکنیم:
- dn: تعداد قطرهای چندضلعی
- n: تعداد راسهای چندضلعی برابر با 8
راس در انواع زاویه ها
تعریف راس زاویه در انواع مختلف زاویهها، یکسان است. با این وجود، برخی از زاویهها، یک راس مشترک دارند.
به عنوان مثال، زاویههای مجاور، زاویههایی هستند یک ضلع و یک راس آنها بر روی یکدیگر منطبق میشود.
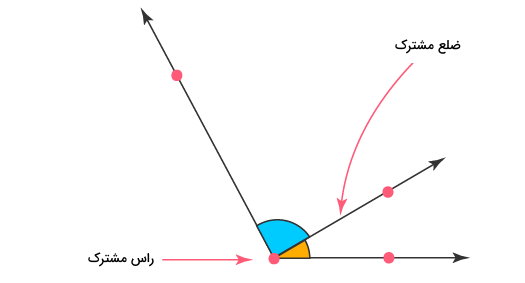
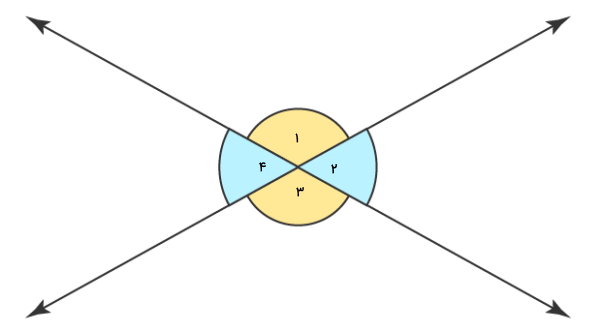
در خطوط متقاطع، چهار زاویه در محل برخورد خطها به وجود میآید. این چهار زاویه، دارای یک راس مشترک هستند. در واقع، محل برخورد دو خط، راس زاویههای متقاطع محسوب میشود.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «زاویه ها و انواع آن ها – هر آنجه باید بدانید» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- زاویه چیست؟ — تعریف، انواع و اندازه گیری
- انواع زاویه چیست ؟ — معرفی تمام زاویه ها — به زبان ساده
- راس زاویه چیست ؟ — به زبان ساده + حل مثال تصویری(همین مطلب)
- زاویه حاده چیست ؟ — به زبان ساده + حل مثال های متنوع تصویری
- زاویه باز چیست ؟ — به زبان ساده + حل مثال های تصویری
- زاویه قائمه چیست ؟ — به زبان ساده + حل مثال های تصویری
- زاویه مکمل چیست ؟ — به زبان ساده + حل تمرین و مثال
- زاویه متمم چیست ؟ — به زبان ساده
- زاویه متقابل به راس چیست ؟ — به زبان ساده + حل تمرین و مثال
- زاویه های مکمل و متمم در هندسه — به زبان ساده
- زاویه نیمصفحه و تعریف آن در هندسه — به زبان ساده
- زاویه محاطی چیست ؟ — اثبات قضیه + حل تمرین و مثال های متنوع
- نیمساز چیست ؟ — به زبان ساده
- اندازه گیری زاویه با نقاله — به زبان ساده + مثال های تصویری
- اندازه گیری زاویه با گونیا — به زبان ساده + مثال های تصویری












