درصد فراوانی ایزوتوپ چیست؟ – به زبان ساده + فرمول و نمونه سوال

اتم‌هایی که در هسته خود تعداد پروتون یکسان و تعداد نوترون متفاوتی دارند ایزوتوپ نامیده می‌شوند. این ایزوتوپ‌ها می‌توانند به صورت مصنوعی یا طبیعی ایجاد شوند. ایزوتوپ‌های یک عنصر به میزان یکسانی در طبیعت وجود ندارند. احتمال وجود برخی از آن‌ها بیشتر و برخی کمتر است. بر همین اساس برای ایزوتوپ‌های مختلف یک عنصر درصد فراوانی ایزوتوپ مشخص می‌کنند. در ادامه ایزوتوپ و نحوه اندازه‌گیری درصد فراوانی ایزوتوپ توضیح داده می‌شود.

درصد فراوانی ایزوتوپ چیست ؟

درصد فراوانی ایزوتوپ به درصدی از اتم با میزان مشخصی از جرم اتمی گفته می‌شود که در طبیعت وجود دارند. ایزوتوپ‌های یک عنصر به میزان یکسان وجود ندارند. برای مثال جیوه 7 ایزوتوپ دارد که ایزوتوپ Hg-202 بیشترین (29٫80٪) و ایزوتوپ Hg-196 کمترین درصد فراوانی ایزوتوپ (0٫146٪) را در میان این هفت ایزوتوپ دارند.

ایزوتوپ چیست ؟

ایزوتوپ از واژه یونانی «Iso» به معنی یکسان و Tope به معنی محل گرفته شده است. به اتم‌هایی که تعداد پروتون یکسان و تعداد نوترون متفاوتی دارند، ایزوتوپ گفته می‌شود که دو زیر گروه دارد.

• ایزوتوپ پایدار
• ایزوتوپ ناپایدار

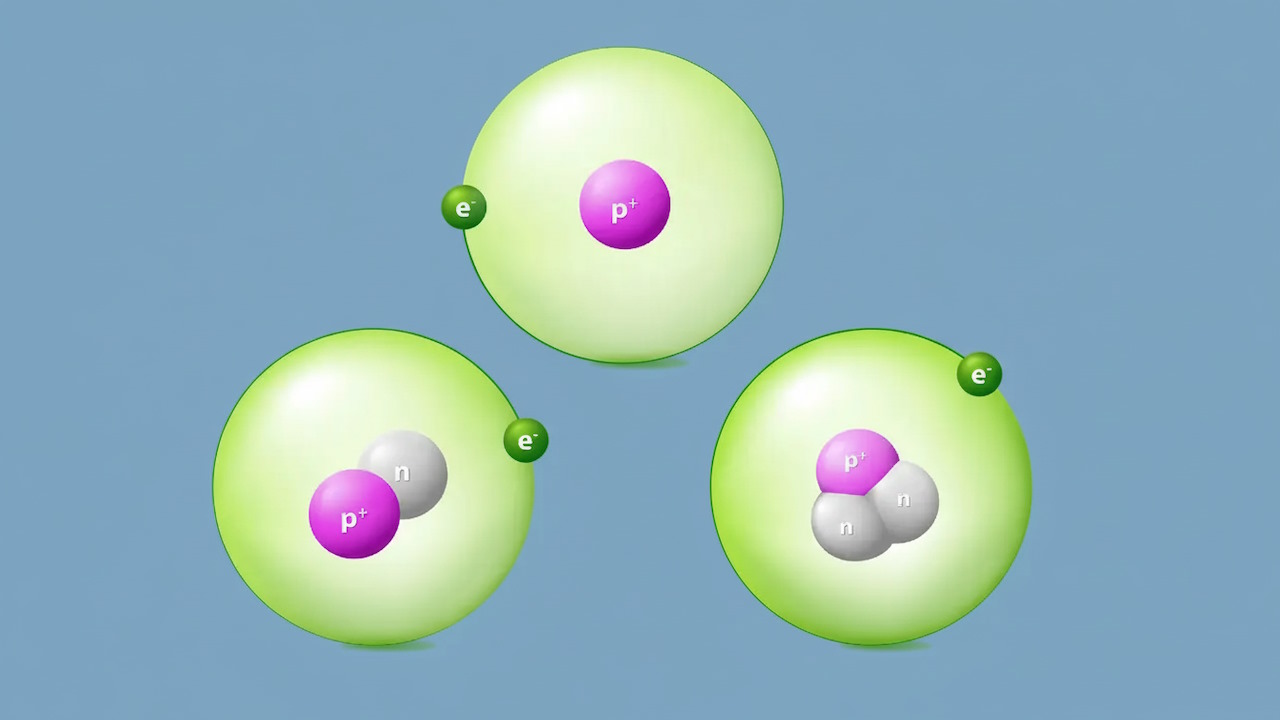
همه چیز از اتم تشکیل شده است و اتم از سه ذره زیراتمی نوترون (خنثی)، الکترون (بار منفی) و پروتون (بار مثبت) تشکیل شده است. پروتون و نوترون در هسته اتم قرار دارند و الکترون در اوربیتال‌ها پیرامون هسته اتم هستند. شکل زیر اتم هلیوم را نشان می‌دهد.

همان‌طور که در تصویر مشاهده می‌کنید هلیوم دارای دو پروتون، دو نوترون و دو الکترون است. عدد اتمی هلیوم 2 است (بر اساس تعداد پروتون) برای این‌که این اتم خنثی باشد دو الکترون نیز در آن با بار مخالف وجود دارد. اگر عدد اتمی یعنی تعداد پروتون‌های اتم تغییر کند به اتمی دیگر تبدیل می‌شود. تعداد الکترون برابر با پروتون نیز برای پایداری اتم اهمیت دارد. با این حال اتم می‌تواند تعداد نوترون متفاوتی داشته باشد و ایزوتوپ‌هایی با جرم اتمی متفاوت ایجاد کند.

از میان عنصرهای جدول تناوبی تنها 21 عنصر «مونوتوپیک» (Monotopic) هستند و یک ایزوتوپ طبیعی دارند و سایر عنصرها دارای ایزوتوپ‌های متعدد هستند.

نقش نوترون در اتم چیست ؟

پروتون‌ها در هسته اتم قرار گرفته‌اند و همگی بار مثبت دارند به همین دلیل، نیروی الکترواستاتیک موجود، آن‌ها را از یکدیگر دور می‌کند. برای این که انسجام هسته اتم حفظ شود نیروی قوی‌تری نسبت به نیروی الکترواستاتیک در هسته وجود دارد که پروتون‌ها را در کنار یکدیگر قرار می‌دهد. این نیروی قوی به دلیل وجود نوترون در هسته به وجود می‌آید.

در اتم‌هایی که جرم اتمی آن‌ها کمتر از 20 است، نسبت نوترون به پروتون برابر با یک نشان‌دهنده پایداری هسته است و در صورتی که اگر این نسبت بیشتر از 1 باشد هسته رادیواکتیو و ناپایدار ایجاد می‌شود. برای مثال در اتم هلیوم میزان نوترون 2 و پروتون نیز 2 عدد است. بر همین اساس نسبت نوترون به پروتون در اتم 1 در نظر گرفته می‌شود که نشان‌دهنده پایداری هسته آن است. در حالی که اتم C-14 دارای ۸ نوترون و 6 پروتون است که نسبت آن بیشتر از یک است. این اتم هسته ناپایدار و رادیواکتیو دارد که به طور خودبخودی متلاشی می‌شود. به این هسته‌ها به‌اصطلاح ایزوتوپ ناپایدار گفته می‌شود.

عدد جرمی و نماد ایزوتوپی

عدد جرمی یک اتم برابر با تعداد پروتون به علاوه تعداد نوترون‌های موجود در هسته اتم است. در شیمی برای نشان دادن میزان پروتون‌ها و نوترون‌های یک عنصر از نماد ایزوتوپی استفاده می‌کنند. در نماد ایزوتوپی عدد جرمی در سمت چپ و بالای نام اتم و عدد اتمی (تعداد پروتون‌های یک اتم) در پایین و سمت چپ اتم نوشته می‌شود. با کم کردن میزان عدد جرمی از عدد اتمی می‌توان میزان نوترون‌ها را محاسبه کرد. اگر عنصر مورد نظر بار الکتریکی هم داشته باشد، بار نیز در سمت راست و بالای نام عنصر نوشته می‌شود.

فراوانی نسبی ایزوتوپ و جرم اتمی میانگین

عنصر کلر دو ایزوتوپ کلر-35 و کلر-37 دارد (کلر-36 به طور مصنوعی تولید می‌شود.). جرم اتمی کلر-35 برابر با ‎‎ ‎‌34٫97 uو جرم اتمی کلر-37 برابر با 36٫97‎ u است. اگر به جدول تناوبی عناصر توجه کنید جرم اتمی عنصر کلر برابر با 35٫45‎ u نوشته شده است. این میزان برابر با میانگین جرم‌های اتمی ایزوتوپ‌های عنصر کلر در طبیعت است. به این جرم اتمی میانگین گفته می‌شود. یکای جرم اتمی میانگین به صورت amu یا u نوشته می‌شود.

اما با محاسبه جرم اتمی میانگین دو ایزوتوپ کلر این سوال پیش می‌آید که چرا جرم اتمی میانگین کلر (35٫45‎ u) با جرم اتمی میانگین ایزوتوپ‌های آن (۳۵٫۹۷) یکسان نمی‌شود؟ یعنی وقتی اعداد 34٫97 و 36٫97 را با هم جمع می‌کنیم و تقسیم بر 2 می‌کنیم عدد ۳۵٫۹۷ بدست می‌آید که با 35٫45‎ نوشته شده در جدول تناوبی متفاوت است.

این تفاوت به دلیل اختلاف فراوانی نسبی این دو ایزوتوپ در طبیعت است. به این معنی که برخی از ایزوتوپ‌ها بیشتر و برخی کمتر در طبیعت وجود دارند. برای مثال در عنصر کلر، ایزوتوپ کلر-35 فراوانی نسبی 75٫76٪ و در ایزوتوپ کلر-37 فراوانی نسبی 24٫24٪ است. به همین علت نمی‌توان جرم اتمی میانگین آن‌ها را تنها با جمع کردن جرم اتمی ایزوتوپ‌ها و سپس تقسیم کردن بر تعداد ایزوتوپ‌ها بدست آورد و باید درصد فراوانی ایزوتوپ‌ها را نیز در نظر گرفت.

فراوانی نسبی معمولا به صورت درصد گزارش می‌شود. برای درک نحوه اندازه‌گیری جرم اتمی میانگین به مثال ارائه شده در بخش بعد مراجعه کنید.

نحوه محاسبه جرم اتمی میانگین به وسیله درصد فراوانی ایزوتوپ

توجه داشته باشید که «جرم اتمی میانگین» (Average Atomic Mass) یک عنصر یک میانگین وزنی است و برای محاسبه آن میزان «جرم اتمی» (Atomic Mass) هر ایزوتوپ در فراوانی نسبی (Relative Abundance) آن ضرب می‌شود سپس نتایج هر یک از ایزوتوپ‌ها با یکدیگر جمع می‌شود. فرمول زیر برای محاسبه آن طراحی شده است.

$$\text{average atomic mass}=sumlimits_{i=1}^n(\text{relative abundance}timestext{atomic mass})_i$$

برای مثال محاسبه جرم اتمی میانگین کلر به صورت زیر عمل می‌کنیم.

$$(0.7576×34.97u)+(0.2424×36.97u)=26.49u+8.96u= 35.45u$$

اندازه گیری درصد فراوانی ایزوتوپ چگونه انجام می‌شود ؟

تا به این قسمت از متن متوجه شدیم که چگونه جرم اتمی میانگین را با استفاده از جرم اتمی ایزوتوپ‌ها و فراوانی نسبی آن‌ها محاسبه کنیم. ولی سوال این است که میزان فراوانی نسبی ایزوتوپ‌ها چگونه بدست می‌آید؟ برای مثال چگونه متوجه می‌شویم که 75٫76٪ از اتم کلر موجود در طبیعت را کلر-35 تشکیل می‌دهد؟

میزان فراوانی نسبی از طریق روشی به نام «طیف سنجی جرمی» (Mass Spectrometry) محاسبه می شود. در این روش نمونه‌ای که دارای اتم‌های مورد نظر است وارد دستگاه می‌شود. نمونه که معمولا در محلول آلی و آبی قرار دارد به سرعت توسط دمای بالا تبخیر می شود و نمونه تبخیر شده توسط الکترون‌های توان بالا بمباران می‌شوند.

این الکترون‌ها انرژی کافی برای جدا کردن الکترون‌ها از اتم‌های نمونه را دارند و در حین انجام این فرایند یون‌های با بار مثبت ایجاد می‌شود. این یون‌ها سپس از طریق صفحات الکتریکی شتاب می‌گیرند و توسط یک میدان مغناطیسی منحرف می‌شوند (به تصویر زیر دقت کنید).

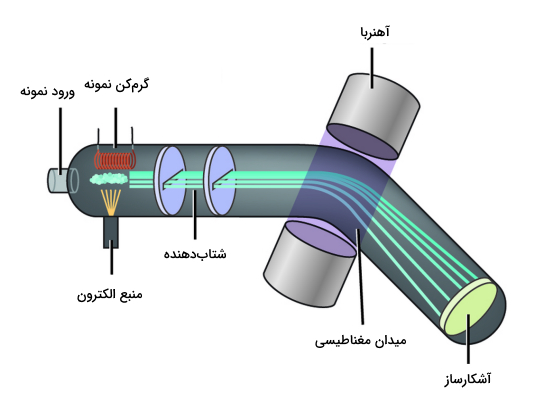
مقدار انحراف هر یون در میدان مغناطیسی به سرعت و بار آن بستگی دارد. یون‌هایی که کندتر حرکت می‌کنند (یعنی یون‌های سنگین‌تر) کمتر منحرف می‌شوند، در حالی که یون‌هایی که سریع‌تر حرکت می‌کنند (یعنی یون‌های سبک‌تر) بیشتر منحرف می‌شوند. برای فهم بهتر این موضوع به نیرویی که برای شتاب دادن به «آجر» نیاز دارید در مقابل نیروی لازم برای شتاب دادن «شن» فکر کنید. نیروی لازم برای شتاب دادن به «شن» بسیار کمتر است. علاوه بر این، میدان مغناطیسی یون‌های با بارهای بالاتر را بیشتر از یون‌هایی با بار کمتر منحرف می‌کند.

مقداری که هر یون منحرف می شود با نسبت جرم به بار آن (m/z)، رابطه عکس دارد. یون‌ها پس از انحراف به یک آشکارساز می‌رسند که دو چیز را اندازه‌گیری می‌کند.

• نسبت جرم به بار هر یون
• تعداد یون‌هایی که نسبت جرم به بار یکسان دارند.

فراوانی نسبی یک یون خاص در نمونه را می‌توان با تقسیم کردن تعداد یون‌ها با نسبت جرم به بار یکسان بر تعداد کل یون‌های شناسایی شده، محاسبه کرد. در پایان آزمایش، دستگاه طیف‌سنج جرمی یک طیف جرمی برای نمونه تولید می‌کند که فراوانی نسبی را در نسبت جرم به بار ترسیم کرده است.

در بعضی از نمونه‌ها تمام یون‌هایی که در دستگاه طیف سنج جرمی ایجاد می‌شوند یک بار مثبت می‌گیرند. در این حالت، نسبت جرم به بار هر یون با جرم یون یا همان جرم اتمی برابر می‌شود. به همین جهت نموداری که برای آن‌ها ارائه می‌شود به جای اینکه در محور X نسبت جرم به بار را نشان دهد، تنها جرم اتمی را نشان می‌دهد.

بررسی طیف جرمی عنصر زیرکونیوم

فرض کنید که نمونه‌ای خالص از عنصر زیرکونیوم با عدد اتمی 40 را در دستگاه طیف‌سنج جرمی قرار داده‌ایم. نمودار زیر نتیجه طیف‌سنجی این عنصر را به ما نشان می دهد.

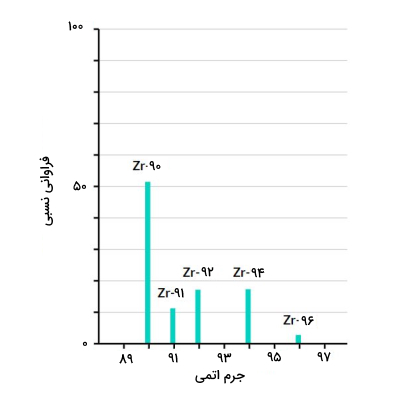
پنج پیک در این نمودار دیده می شود که نشان‌دهنده پنج ایزوتوپ طبیعی عنصر زیرکونیوم هستند. میزان بلندی هر پیک نشان‌دهنده میزان فراوانی آن ایزوتوپ به نسبت سایر ایزوتوپ‌های عنصر زیرکونیوم است. در مورد عنصر زیرکونیوم ایزوتوپ Zr-90 بیشترین فراوانی را دارد.

نحوه محاسبه درصد فراوانی ایزوتوپ

برای درک بهتر نحوه اندازه‌گیری درصد فراوانی ایزوتوپ‌ها در ادامه چند مثال برای عناصر مس، سیلیکون و سرب آورده شده است.

مثال اول: محاسبه درصد فراوانی ایزوتوپ‌های عنصر مس

جرم اتمی مس 63٫546‎ ± ‎0٫003‎‎ amu است. Cu-63 و Cu-65 ایزوتوپ‌های مس هستند. جرم اتمی Cu-63 برابر با ‎62٫9296 amu و جرم اتمی Cu-65 برابر با ‎64٫9278 amu است. درصد فراوانی ایزوتوپ‌های آن را حساب کنید.

برای بدست آوردن درصد فراوانی ایزوتوپ‌ها از معادله زیر استفاده می‌کنیم.

$$\text{average atomic mass}=sumlimits_{i=1}^n(\text{relative abundance}timestext{atomic mass})_i$$

با جایگزین کردن مقادیر گزارش شده در سوال به معادله زیر می‌رسیم.

$$63٫546 = (62٫9296 × Cu-63) + (64٫9278 × Cu-65)$$

این را می‌دانیم که میزان درصد فراوانی Cu-68 + Cu-63 برابر با 100 است. از این رو این معادله را بر اساس درصد فراوانی یکی از ایزوتوپ‌ها (Cu-63) می‌نویسیم. همچنین برای ساده‌تر شدن محاسبات دو طرف نمودار را بر 100 تقسیم می‌کنیم. در این حالت مجموع درصد فراواتنی ایزوتوپ‌ها برابر با 1 می‌شود.

$$Cu^{63} + Cu^{68} = 1$$

$$Cu^{68} = 1 - Cu^{63}$$

این عبارت را در معادله اصلی اضافه می‌کنیم.

$$(Cu^{63}times62.9296) +( 1 - Cu^{63}times64.9278)=63.54$$

$$Cu^{63}times62.9296 +64.9278-(Cu^{63}times64.9278)=63.54$$

$$62.9296( Cu^{63})+64.9278-64.9278(Cu^{63})=63.54$$

$$-1.9982(Cu^{63})=-1.3878$$

$$(Cu^{63})=\frac{1.3878}{1.9982}$$

$$Cu^{63}=69.4525$$

با کم کردن مقدار درصد فراوانی ایزوتوپ Cu-63 از عدد 100 می‌توان مقدار درصد فراوانی ایزوتوپ Cu-65 را بدست آورد.

$$Cu^{68}=30.5475$$

مثال دوم: محاسبه درصد فراوانی ایزوتوپ‌های عنصر سیلیکون

عنصر سیلیکون سه ایزوتوپ طبیعی با جرم‌های اتمی زیر را دارد. اگر جرم اتمی میانگین عنصر سیلیکون ‎28٫0855 amu باشد و درصد فراوانی Si-29 برابر با 4٫6٪ باشد، درصد فراوانی ایزوتوپ‌های Si-29 و Si-29 را محاسبه کنید.

• جرم اتمی ایزوتوپ Si-28 برابر با 27.9769‎ amu
• جرم اتمی ایزوتوپ Si-29 برابر با 28٫9765‎ amu
• جرم اتمی ایزوتوپ Si-30 برابر با 29٫9738‎ amu

برای حل این مسئله ایزوتوپ Si-28 را x و ایزوتوپ Si-30 را y در نظر می‌گیریم. می‌دانیم که جرم اتمی میانگین از فرمول زیر محاسبه می‌شود.

جرم اتمی میانگین عنصر سیلیکون= (درصد فراوانی Si-28 × جرم اتمی Si-28) + (درصد فراوانی Si-29 × جرم اتمی Si-29) + (درصد فراوانی Si-30 × جرم اتمی Si-30)

همچنین می‌دانیم که مجموع درصد فراوانی ایزوتوپ‌های یک عنصر برابر با 100 است. برای این که معادله ساده شود این معادله را به 100 تقسیم می‌کنیم که در این صورت مجموع درصد فراوانی‌های یک ایزوتوپ برابر با 1 می‌شود.

$$x + y + 0.0467= 1$$

معادله را بر اساس یکی از ایزوتوپ‌ها می‌نویسیم.

$$y=1-0.0467-x$$

$$y=0.9533-x$$

حال به جای y در معادله اول از نتیجه بدست آمده استفاده می‌کنیم.

$$(xtimes27.9769)+((0.9533-x)times29.9738)+(0.0467times28.9765)=28.0855$$

$$27.9769x+28.574-29.9738x=26.7322$$

$$-1.9969x=-1.8418$$

$$x=0.922$$

مقدار بدست امده از x را در 100 ضرب می‌کنیم تا درصد فراوانی ایزوتوپ Si-28 بدست آید.

$$x=92.2٪$$

سپس مقدار بدست آمده از x را در فرمول زیر جایگزاری می‌کنیم تا مقدار ایزوتوپ Si-30 بدست آید.

$$0.922 + y + 0.0467= 1$$

$$y = 0.031$$

$$y = 3.1$$

مثال سوم: محاسبه درصد فراوانی ایزوتوپ‌های عنصر سرب

جرم اتمی میانگین عنصر سرب برابر با 207٫19‎ amu است. این عنصر دارای سه ایزوتوپ است که جرم اتمی آن‌ها در بخش زیر نوشته شده است. اگر درصد فراوانی نسبی ایزوتوپ‌های Pb-207 و Pb-208 برابر باشد، درصد فراوانی هر سه ایزوتوپ را بدست آورید.

• جرم اتمی ایزوتوپ Pb-206 برابر با 205.98‎ amu
• جرم اتمی ایزوتوپ Pb-207 برابر با 206.98‎ amu
• جرم اتمی ایزوتوپ Pb-208 برابر با 207.98‎ amu

طبق صورت مسئله درصد فراوانی ایزوتوپ‌های Pb-207 و Pb-208 برابر است پس هر دو را x در نظر می‌گیریم. ایزوتوپ Pb-206 را نیز y در نظر می‌گیریم. می‌دانیم که مجموع درصد فراوانی‌ ایزوتوپ‌های یک عنصر برابر با 100 است. برای راحتی آن را 1 در نظر می‌گیریم و در آخر اعداد بدست امده را در 100 ضرب می‌کنیم. بر همین اساس می‌توانیم فرمول زیر را بنویسیم.

$$y+x+x=1$$

$$y=2x$$

y را بر اساس x در فرمول می‌نویسیم.

$$(205.98) (x) + (206.98) (x) + (207.98) (1 − 2x) = 207.19$$

$$x = 0.263$$

درصد فراوانی ایزوتوپ‌های Pb-207 و Pb-208 برابر با 26٫3٪ بدست آمد و درصد فراوانی y دو برابر x است که میزان آن 47٫4٪ می‌شود.

جمع‌بندی

ایزوتوپ‌های یک عنصر در تعداد نوترون با یکدیگر تفاوت دارند به همین جهت جرم اتمی متفاوت برای عنصر به وجود می‌آورند. این ایزوتوپ‌ها به طور یکسان در طبیعت وجود ندارند. بعضی بیشتر و بعضی کمتر هستند. به درصدی از این ایزوتوپ‌ها که در طبیعت وجود دارند،‌ درصد فراوانی ایزوتوپ گفته می‌شود. برای اندازه‌گیری درصد فراوانی ایزوتوپ‌ها از دستگاه طیف‌سنجی جرمی استفاده می‌شود. درصد فراوانی ایزوتوپ‌ها برای محاسبه جرم اتمی میانگین اتم اهمیت دارد و در فرمول محاسبه آن به کار می‌رود.