حد بینهایت — به زبان ساده

یکی از مفاهیم بسیار مهم در ریاضیات، مفهوم حد است. حد کاربرد بسیار زیادی در محاسبات مختلف ریاضی و فیزیک و مفاهیم پایه مهندسی دارد. در مطالب قبلی وبلاگ فرادرس مفهوم حد در ریاضی به صورت کلی مورد بررسی قرار گرفت. این مطلب به صورت دقیق به بررسی حد بینهایت می‌پردازد. توجه کنید که حد بینهایت زمانی رخ می‌دهد که مقدار حد برابر با بینهایت و یا منفی بینهایت باشد.

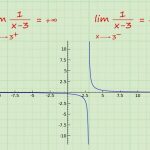
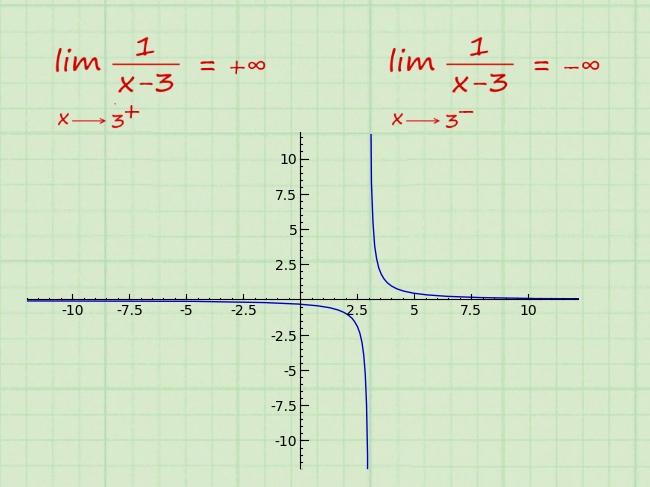
همانطور که اشاره شد، در بسیاری از مباحث ریاضی و مهندسی، ممکن است که با حد بینهایت مواجه شویم. بنابراین آموزش دقیق این نوع از حد می‌تواند کمک زیادی به درک مسائل مختلف ریاضی و مهندسی بکند. بر این اساس اولین گام، ارائه تعریف درستی از حد بینهایت در ریاضیات است. همچنین حالتی نیز وجود دارد که در آن، مقدار حد به سمت بینهایت میل می‌کند که در مبحث «حد در بینهایت — به زبان ساده» به بررسی این موضوع پرداخته شده است.

تعریف حد بینهایت

همانطور که اشاره شد، حد بینهایت حالتی است که مقدار حد در یک نقطه خاص برابر با بینهایت و یا منفی بینهایت شود. حالت اول را می‌توان با استفاده از رابطه زیر بیان کرد.

$$\large \mathop { \lim } \limits _ { x \to a} f \left ( x \right ) = \infty$$

این رابطه نشان می‌دهد که مقدار تابع (f(x زمانی که مقدار x به سمت a میل می‌کند، برابر با مقادیر بسیار بزرگ می‌شود و این مقادیر بسیار بزرگ را می‌توان با استفاده از علامت ∞ نمایش داد که این علامت، بینهایت نامیده می‌شود. در حالت منفی بینهایت نیز می‌توان حد بینهایت را به شکل زیر تعریف کرد.

$$\large \mathop { \lim } \limits _ { x \to a } f \left ( x \right ) = - \infty$$

تعاریف ارائه شده در بالا را می‌توان برای حالات مختلف مربوط به حد یک طرفه نیز بیان کرد. در ادامه و با استفاده از چند مثال، مفهوم حد بینهایت برای توابع مختلف را مورد بررسی قرار می‌دهیم.

مثال 1

تابع $$1 \over x$$ را در نظر بگیرید. حد این تابع را در سه حالت زیر مورد محاسبه قرار دهید.

$$\large \mathop { \lim } \limits _ { x \to { 0 ^ + } } \frac { 1 } { x } \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to { 0 ^ - } } \frac { 1 } { x } \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to 0 } \frac { 1 } { x }$$

عبارت اول سمت چپ، حد تابع $$1 \over x$$ را در حالتی نشان می‌دهد که پارامتر x از مقادیر مثبت (مقدار مثبت محور مختصات) به سمت صفر میل می‌کند. بنابراین برای محاسبه حد عبارت اول، جدول زیر را تشکیل می‌دهیم.

همانطور که مشاهده می‌شود، با کاهش مقدار x و نزدیک شدن به صفر، مقدار تابع $$1 \over x$$ افزایش می‌یابد و به سمت بی‌نهایت میل می‌کند. بنابراین می‌توان نتیجه گرفت که حد راست تابع $$1 \over x$$ زمانی که x به سمت صفر مثبت میل می‌کند برابر با ∞+ است.

حال به بررسی حد رابطه وسط موجود در صورت سوال می‌پردازیم. برای محاسبه این حد، جدولی را به شکل زیر تشکیل می‌دهیم.

همانطور که مشاهده می‌شود، زمانی که از سمت مقادیر منفی، به عدد صفر نزدیک می‌شویم، مقدار تابع $$1 \over x$$ هر لحظه کوچکتر می‌شود و به سمت منفی بینهایت میل می‌کند. بر این اساس می‌توان نتیجه گرفت که حد تابع $$1 \over x$$ زمانی که متغیر x به سمت صفر منفی میل می‌کند، برابر با منفی بینهایت (∞-) است.

با توجه به توضیحاتی که داده شد، حد تابع $$1 \over x$$ زمانی که مقدار x به سمت صفر مثبت یا صفر منفی میل می‌کند را محاسبه کردیم.

$$\large \mathop { \lim } \limits _ { x \to { 0 ^ + } } \frac { 1 } { x } = \infty \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to { 0 ^ - } } \frac { 1 } { x } = - \infty$$

یکی از روش‌های دیگر برای محاسبه حد در یک نقطه این است که تابع را در نزدیکی نقطه مورد نظر رسم کنیم. بنابراین برای محاسبه حد این تابع، منحنی تابع $$1 \over x$$ را در حوالی نقطه 0 به شکل زیر رسم می‌کنیم.

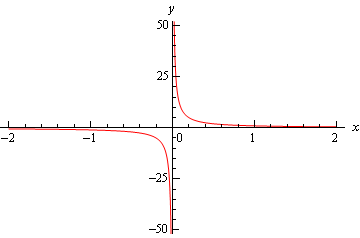
همانطور که در شکل بالا مشاهده می‌شود، زمانی که از سمت مقادیر مثبت به صفر نزدیک می‌شویم، مقدار تابع به سمت بینهایت میل می‌کند و زمانی که از سمت مقادیر منفی به صفر نزدیک شویم، مقدار تابع به سمت منفی بینهایت میل می‌کند.

برای محاسبه عبارت سوم صورت سوال، یعنی محاسبه حد تابع $$1 \over x$$ در نقطه x باید از تعریف حد استفاده کنیم. همانطور که می‌دانیم، یک تابع زمانی در یک نقطه حد دارد که مقدار حد چپ و راست آن تابع در نقطه مورد نظر یکسان باشد.

بنابراین از آنجایی که مقدار حد راست تابع مورد نظر در نقطه صفر، برابر با ∞ و مقدار حد چپ آن برابر با ∞- است، می‌توان نتیجه گرفت که تابع $$1 \over x$$ در نقطه صفر، حد ندارد. بنابراین می‌توان به صورت خلاصه پاسخ مثال را با استفاده از روابط زیر بیان کرد.

$$\large \mathop { \lim } \limits _ { x \to { 0 ^ + } } \frac { 1 } { x } = \infty \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to { 0 ^ - } } \frac { 1 } { x } = - \infty$$

همچنین باید بیان کرد که تابع مورد نظر در نقطه صفر، حد ندارد.

در ادامه یک مثال بیان می‌شود که در آن تنها عبارت x در مخرج حضور نداشته باشد. البته توجه کنید که برای محاسبه این حد نیز، باید روندی مشابه با روند مثال اول طی شود.

مثال 2

هرکدام از حدهای نشان داده شده در روابط زیر را محاسبه کنید.

$$\large \mathop { \lim } \limits _ { x \to - { 2 ^ + } } \frac { { - 4 } } { { x + 2 } } \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to - { 2 ^ - } } \frac { { - 4 } } { { x + 2 } } \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to - 2 } \frac { { - 4 } } { { x + 2 } }$$

در این مثال نیز مشابه مثال قبل، از حد راست در نقطه داده شده، شروع می‌کنیم. برای حد راست رابطه بالا می‌توانیم رابطه زیر را بیان کنیم.

$$\large x > - 2 \hspace { 0.5 in } \, \, \, \, \, \, \Rightarrow \hspace { 0.5 in } x + 2 > 0$$

بنابراین زمانی که مقدار متغیر x از سمت مثبت به مقدار 2- میل کند، مقدار x+2 از سمت مثبت به صفر میل می‌کند. بنابراین در این حالت کسر $$\mathop { \lim } \limits _ { x \to - { 2 ^ + } } \frac { { - 4 } } { { x + 2 } }$$ برابر با حاصل تقسیم یک عدد منفی (4-) بر صفر مثبت (x+2) است. بر این اساس می‌توان نتیجه گرفت که مقدار آن برابر با ∞- است.

روندی که برای $$x > - 2$$ طی شد را می‌توان برای حد چپ در نقطه $$x = - 2$$ نیز بیان کرد. بنابراین داریم:

$$\large x < - 2 \hspace { 0.5 in } \, \, \, \, \, \, \Rightarrow \hspace { 0.5 in } x + 2 < 0$$

بر این اساس، در حالتی که حد چپ تابع در نقطه $$x = - 2$$ مد نظر ما است، مقدار $$x + 2$$ منفی است. بنابراین حد تابع زیر را می‌توان برابر با حاصل تقسیم یک عدد منفی (4-) بر صفر منفی (x+2) دانست که این مقدار برابر با ∞ است.

$$\large \mathop { \lim } \limits _ { x \to - { 2 ^ - } } \frac { { - 4 } } { { x + 2 } }$$

برای درک بهتر حد این تابع، می‌توانیم منحنی تابع مورد نظر را در محدوده نزدیک نقطه $$x = - 2$$ رسم کنیم. این منحنی در شکل زیر نشان داده شده است.

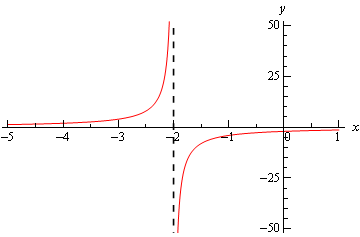
همانطور که مشاهده می‌شود، حد راست تابع در نقطه $$x = - 2$$ برابر با ∞- و حد چپ این تابع در نقطه $$x = - 2$$ برابر با ∞ است. این موضوع را می‌توان با استفاده از رابطه زیر هم نشان داد.

$$\large \mathop { \lim } \limits _ { x \to - { 2 ^ + } } \frac { { - 4 } } { { x + 2 } } = - \infty \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to - { 2 ^ - } } \frac { { - 4 } } { { x + 2 } } = \infty$$

دقت کنید که با توجه به روابط بالا، تابع $$\frac { { - 4 } } { { x + 2 } }$$ در نقطه $$x = - 2$$ حد ندارد. دلیل این موضوع این است که حد راست تابع برابر با ∞- و حد چپ آن برابر با ∞ است و زمانی که حد راست و چپ تابعی در یک نقطه برابر نباشند، آن تابع در نقطه مورد نظر، حد ندارد.

مجانب عمودی

توجه کنید که در هر دو مثال بیان شده، توابع مورد نظر، دارای مجانب عمودی هستند. برای مثال، تابع معرفی شده در مثال 2، در نقطه $$x = - 2$$ مجانب عمودی دارد و تابع مورد نظر در این نقطه به سمت مثبت و منفی بینهایت میل می‌کند.

بنابراین با توجه به روابط بیان شده در حد بینهایت می‌توان مجانب عمودی توابع مختلف را مورد محاسبه قرار داد. تعریف مجانب عمودی تابع (f(x را می‌توان با استفاده از روابط زیر بیان کرد.

طبق تعریف، اگر هرکدام از شرط‌های زیر ارضا شود، تابع (f(x در نقطه x=a مجانب عمودی دارد.

$$\large \mathop { \lim } \limits _ { x \to {a ^ - } } f \left ( x \right ) = \pm \, \infty \hspace { 0.25 in } \mathop { \lim } \limits _ { x \to { a ^ + } } f \left ( x \right) = \pm \, \infty \hspace { 0.25 in } \mathop { \lim } \limits _ { x \to a} f \left ( x \right) = \pm \, \infty$$

توجه کنید که برای این که یک تابع در نقطه x=a مجانب عمودی داشته باشد، تنها لازم است که یکی از حدهای بالا برقرار باشد. بنابراین با استفاده از این روابط می‌توان بیان کرد که تابع $$1 \over x$$ در مثال 1، در نقطه $$x = 0$$، مجانب عمودی دارد و مجانب عمودی تابع $$\frac { { - 4 } } { { x + 2 } }$$ در نقطه $$x = - 2$$، قرار گرفته است.

دقت کنید که هدف ما در این مطلب بررسی مجانب عمودی نیست ولی با توجه به اینکه این تعریف مجانب عمودی و حد بینهایت دارای اشتراک‌های زیادی هستند، لازم بود که تعریف این مفهوم (مجانب عمودی) در این مطلب به صورت دقیق بیان شود.

ادامه مثال‌ها

در قسمت قبل، دو مثال برای مفهوم حد بینهایت بیان شد. در ادامه به بررسی چند مثال سخت‌تر برای درک بهتر مفهوم حد بینهایت و انجام محاسبات در این زمینه پرداخته می‌شود.

مثال 3

حدهایی که در رابطه زیر نشان داده شده را محاسبه کنید و همچنین حد تابع داده شده را در نقطه $$x = 4$$ به دست آورید.

$$\large \mathop { \lim } \limits _ { x \to { 4 ^ + } } \frac { 3 } { { { { \left ( { 4 - x } \right ) } ^ 3 } } } \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to { 4 ^ - } } \frac { 3 }{ { { { \left ( { 4 - x } \right ) } ^ 3 } } } \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to 4 } \frac { 3 } { { { { \left ( { 4 - x } \right ) } ^ 3 } } }$$

برای پاسخ به سوال بالا، ابتدا از حد راست تابع در نقطه $$x = 4$$ شروع می‌کنیم. در این حالت روابط زیر برقرار هستند.

$$\large x > 4 \hspace { 0.5 in } \Rightarrow \hspace { 0.25 in } 4 - x < 0 \hspace { 0.25 in } \Rightarrow \hspace { 0.5 in } { \left ( { 4 - x } \right ) ^ 3 } < 0$$

همانطور که مشاهده می‌شود، زمانی که از مقادیر بیشتر از 4 به این عدد نزدیک می‌شویم، مخرج تابع داده شده عبارتی منفی (صفر منفی) خواهد شد. بنابراین کسر را می‌توان به صورت حاصل تقسیم یک عدد مثبت (3) بر یک عدد منفی (صفر منفی) نوشت که حاصل آن برابر با منفی بینهایت (∞-) می‌شود.

در ادامه و برای محاسبه حد چپ تابع مورد نظر در نقطه $$x = 4$$، نیاز به تعیین علامت مخرج کسر داده شده داریم. برای تعیین علامت مخرج این کسر، از رابطه زیر برای حد چپ استفاده می‌کنیم.

$$\large x < 4 \hspace { 0.5 in } \Rightarrow \hspace { 0.25 in } 4 - x > 0 \hspace { 0.25 in } \Rightarrow \hspace { 0.5 in } { \left ( { 4 - x } \right ) ^ 3 } > 0$$

با دقت به روابط بالا، متوجه می‌شویم که وقتی از سمت چپ به عدد چهار نزدیک شویم، مخرج کسر صورت سوال، برابر با مقدار مثبت می‌شود. این مقدار مثبت را صفر مثبت نیز می‌نامد. بنابراین حد چپ کسر داده شده و در نقطه $$x = 4$$، برابر با حاصل تقسیم عدد مثبت (3) بر صفر مثبت است. این مقدار برابر با بینهایت (∞) خواهد بود.

بنابراین همانطور که توضیح داده شد، حد راست تابع داده شده در نقطه $$x = 4$$ برابر با منفی بینهایت (∞-) و حد چپ در این نقطه برابر با مثبت بینهایت (∞) شده است. از آنجایی که حد چپ و راست تابع داده شده در این نقطه با یکدیگر برابر نیستند، می‌توان نتیجه گرفت که این تابع در نقطه $$x = 4$$، حد ندارد. این موضوع در رابطه زیر نشان داده شده است.

$$\large \mathop { \lim } \limits _ { x \to { 4 ^ + } } \frac { 3 } { { { { \left ( { 4 - x } \right ) } ^ 3 } } } = - \infty \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to { 4 ^ - } } \frac { 3 } { { { { \left ( { 4 - x } \right ) } ^ 3 } } } = \infty$$

با دقت به تعریف مجانب، متوجه می‌شویم که این تابع در نقطه $$x = 4$$، مجانب عمودی دارد. برای بررسی دقیق این موضوع نمودار این تابع را به شکل زیر رسم می‌کنیم.

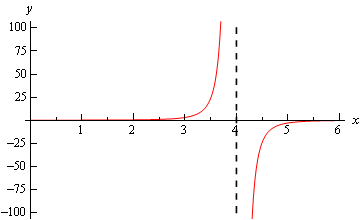
حد راست و چپ تابع را با استفاده از شکل بالا نیز می‌توانیم محاسبه کنیم. پیشنهاد ما برای درک بهتر مبحث حد بینهایت، این است که حد‌های محاسبه شده در این مثال را با شکل بالا مقایسه کنید.

تمام مثال‌هایی که تاکنون به بررسی آن‌ها پرداخته شد، مثال‌های مربوط به عبارات گویا و کسری بودند. اما توابع دیگری نیز مانند $$\ln$$ و $$\tan$$ وجود دارند که در برخی حالات برابر با بینهایت می‌شوند و بنابراین حد بینهایت دارند. دو مثال بعدی به بررسی این موضوع در مبحث حد بینهایت می‌پردازد.

مثال 4

حد راست تابع نشان داده شده را در نقطه $$x = 0$$ محاسبه کنید.

$$\large \mathop { \lim } \limits _ { x \to { 0 ^ + } } \ln \left ( x \right )$$

همانطور که می‌دانیم، دامنه تابع لگاریتمی شامل مقادیر مثبت است. بنابراین در این مثال تنها حد راست تابع مورد نظر در نقطه $$x = 0$$ مد نظر ما است و حد چپ این تابع موجود نمی‌باشد و نمی‌توان درباره آن نظری داد. بر این اساس نمودار تابع را در محدوده اعداد مختلف x به شکل زیر رسم می‌کنیم.

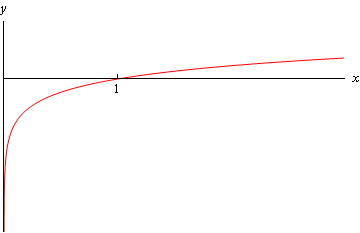
همانطور که مشاهده می‌شود، حد راست تابع $$\ln ( x )$$ در نقطه $$x = 0$$ برابر با منفی بینهایت (∞-) است و رابطه زیر به خوبی این موضوع را نشان می‌دهد.

$$\large \mathop { \lim } \limits _ { x \to { 0 ^ + } } \ln \left ( x \right ) = - \infty$$

همانطور که مشاهده می‌شود، دانستن دامنه و برد یک تابع اهمیت بسیار زیادی در محاسبه حد توابع و حد بینهایت دارد. مطلب «دامنه و برد تابع — به زبان ساده» در وبلاگ فرادرس به بررسی تعریف دامنه و برد توابع مختلف پرداخته است.

مثال 5

این مثال به بررسی یکی از توابع مثلثاتی یعنی $$\tan$$ که حد بینهایت دارد می‌پردازد. بنابراین حد نشان داده شده در رابطه زیر را محاسبه کنید.

$$\large \mathop { \lim } \limits _ { x \to { { \frac { \pi } { 2 } } ^ + } } \tan \left ( x \right ) \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to { { \frac { \pi } { 2 } } ^ - } } \tan \left ( x \right )$$

برای محاسبه سریع حد‌های داده شده، نمودار این تابع مثلثاتی را در محدوده xهای مختلف رسم می‌کنیم. شکل زیر نمودار این تابع را نشان می‌دهد.

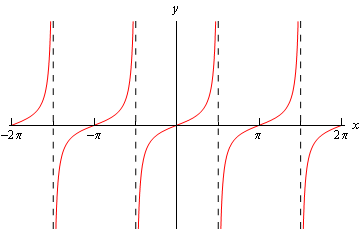
بنابراین همانطور که مشاهده می‌شود، تابع مورد نظر در نقطه $$\frac { \pi } { 2 }$$ مجانب دارد. بر این اساس می‌توان بیان کرد که حد راست تابع $$\tan ( x )$$ در نقطه $$\frac { \pi } { 2 }$$ برابر با منفی بینهایت (∞-) و حد چپ آن برابر با مثبت بینهایت (∞) است.

همانطور که بیان شد و با توجه به یکسان نبودن حد چپ و راست در این نقطه، می‌توان بیان کرد که این تابع در نقطه $$\frac { \pi } { 2 }$$ حد ندارد. رابطه زیر به صورت ریاضی، حد راست و چپ این تابع را نشان داده است.

$$\large \mathop { \lim } \limits _ { x \to { { \frac { \pi } { 2 } } ^ + } } \tan \left ( x \right ) = - \infty \hspace { 0.5 in } \mathop { \lim } \limits _ { x \to { { \frac { \pi } { 2 } } ^ - } } \tan \left( x \right ) = \infty$$

نکات تکمیلی حد بینهایت

در ادامه چند نکته تکمیلی درباره حد بینهایت مورد بررسی قرار می‌گیرد. بنابراین دو تابع $$f ( x )$$ و $$g ( x )$$ را در نظر بگیرید که روابط زیر در آن‌ها برقرار باشد.

$$\large \mathop { \lim } \limits _ { x \to c } f \left ( x \right ) = \infty \hspace { 0.5 in } \hspace { 0.25 in } \mathop { \lim } \limits _ { x \to c} g \left ( x \right ) = L$$

برای حالتی که L و c اعداد حقیقی باشند، 4 رابطه زیر را می‌توان در مبحث حد بینهایت بیان کرد.

• $$\large \mathop { \lim } \limits _ { x \to c } \left [ { f \left ( x \right ) \pm g \left ( x \right ) } \right ] = \infty$$

• اگر $$\large L > 0$$ باشد، آنگاه $$\large \mathop { \lim } \limits _ { x \to c } \left [ { f \left ( x \right ) g \left ( x \right ) } \right ] = \infty$$

• اگر $$\large L < 0$$ باشد، آنگاه $$\large \mathop { \lim } \limits _ { x \to c } \left [ { f \left ( x \right ) g \left ( x \right ) } \right ] = - \infty$$
• $$\large \displaystyle \mathop { \lim } \limits _ { x \to c } \frac { { g \left ( x \right ) } } { { f \left ( x \right ) } } = 0$$

این روابط، کاربرد بسیار زیادی در مسائل مختلف و همچنین محاسبه حد ترکیب توابع و توابع پیچیده دارند. نکته دیگری که باید توجه کرد این است که این روابط برای حدهای یک طرفه نیز کاربرد دارند و تنها با تعویض نوع حد می‌توان روابط را بازنویسی کرد.

یکی دیگر از مواردی که در این بخش باید به بررسی آن پرداخت این است که این روابط را می‌توان برای حد منفی بینهایت یعنی $$\mathop { \lim } \limits _ { x \to c } f \left ( x \right ) = - \infty$$ نیز بازنویسی کرد. برای این کار کافی است که علامت بینهایت در سه رابطه اول را در علامت منفی ضرب کنیم.

در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقه‌مند هستید، آموز‌ش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی
• مجموعه آموزش‌های ریاضیات
• دامنه و برد تابع — به زبان ساده
• حد در ریاضی — به زبان ساده
• حد در بینهایت — به زبان ساده
• اعداد گویا — به زبان ساده
• اتحاد و تجزیه در ریاضی — به زبان ساده
• بی نهایت و مفهوم آن — به زبان ساده

^^