اعداد با توان منفی — به زبان ساده

در این آموزش از مجموعه آموزش‌های ریاضی مجله فرادرس با روش محاسبه اعداد با توان منفی آشنا می‌شویم.

ابتدا لازم است یادآوری کنیم که برای مثال، در عدد $$2 ^ 5$$، عدد $$2$$ را مبنا یا پایه و $$5$$ را توان می‌نامیم. به طور مشابه، در $$3 ^ {-4}$$، عدد $$3$$ پایه و $$-4$$ توان است.

مشابه سایر اعداد توان‌دار، اعدادی که توان منفی دارند نیز از قواعد مشخص و ساده‌ای پیروی می‌کنند. هفت قانون مهم مربوط به اعداد توان‌دار که اعداد با توان منفی را نیز شامل می‌شود، به صورت زیر هستند:

1. ضرب توان‌ها: در ضرب اعدادی با پایه مشابه، توان‌ها را با هم جمع می‌کنیم.
2. تقسیم توان‌ها: در تقسیم اعدادی با پایه مشابه، توان‌ها را از هم کم می‌کنیم.
3. توان توان‌ها: وقتی یک توان به توان عددی دیگر برسد، توان را در آن عدد ضرب می‌کنیم.
4. توان ضرب دو عدد: وقتی ضرب دو عدد را به توان برسانیم، باید توان را بر هر دو عدد اعمال کنیم.
5. توان تقسیم دو عدد: وقتی تقسیم دو عدد را به توان عددی برسانیم، باید توان را بر هر دو عدد اعمال کنیم.
6. قانون توان صفر: هر عدد به توان صفر برابر با یک است.
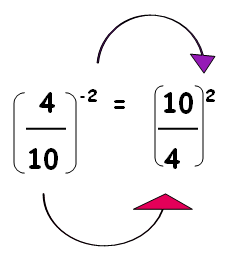
7. قانون توان منفی: برای تغییر توان منفی به مثبت، پایه را عکس کرده و حاصل را به توان مثبت می‌رسانیم.

اعداد منفی

ابتدا به اعداد منفی اشاره‌ کوتاهی می‌کنیم تا درک توان منفی نیز ساده‌تر شود. شاید ساده‌ترین پاسخ به این پرسش که عدد منفی چیست، این باشد: «عدد منفی هر عددی است که کوچک‌تر از صفر است.»

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

اعداد منفی روی محور اعداد زیر با رنگ قرمز نشان داده شده‌اند.

وقتی یک عدد منفی را از عددی دیگر کم می‌کنیم، در واقع به سمت راست محور اعداد می‌رویم، زیرا مشابه افزودن یک عدد مثبت است. به طور مشابه، وقتی یک عدد منفی را به عددی دیگر جمع می‌کنیم، در واقع، به سمت چپ حرکت می‌کنیم، زیرا مشابه این است که یک عدد مثبت را کم می‌کنیم.

$$\large - 5 + 4 = - 1$$

$$\large 6 - ( - 2 ) = 8$$

وقتی یک عدد منفی را در یک عدد مثبت ضرب می‌کنیم (یا بالعکس)، حاصل‌ضرب منفی خواهد بود. همچنین، اگر دو عدد منفی یا دو عدد مثبت را در هم ضرب کنیم، حاصل آن مثبت است.

$$\large - 3 \times - 7 = 21$$

$$\large - 3 \times 7 = - 21$$

ضرب علامت‌های متفاوت در یکدیگر، همیشه حاصلی منفی خواهد داشت و حاصل‌ضرب دو عدد هم‌علامت همواره مثبت است. اگر عددی دارای علامت نباشد، بدین معنی است که مثبت است.

توان منفی چیست؟

قبلاً با توان مثبت آشنا شده‌ایم و می‌دانیم که توان به معنی تکرار ضرب است. برای مثال، $$4 ^ 3$$ (چهار به توانِ سه) یعنی $$4$$ را سه بار ضرب در خودش کنیم:

$$\large 4 ^ 3 = 4 \times 4 \times 4 = 64$$

فیلم آموزش ریاضی – پایه نهم در فرادرس

کلیک کنید

توان منفی نیز با کمی تغییرات، تعریف مشابهی با توان مثبت دارد. اما در حالت کلی می‌توان گفت که توان منفی در واقع مخالف توان مثبت است.

همه توان‌ها یا همان نماهای منفی را می‌توان با وارون کردن عدد پایه و مثبت کردن توان نشان داد. اما منظور از وارون چیست؟ وارون یا عکس یک عدد کسری، در واقع کسری است که در آن، جای صورت و مخرج تغییر کرده است. بدین ترتیب، $$5 ^{-3}$$ به صورت زیر محاسبه می‌شود:

$$\large 5 ^{-3} = \frac { 1 } { 5 ^ 3 }$$

در حقیقت، وقتی یک عدد به توان عدد منفی می‌رسد، آن عدد وارون شده و توان مثبت می‌شود. همان عدد $$5 ^{ - 3 }$$ را در نظر بگیرید. طبق چیزی که گفتیم، ابتدا خود عدد پایه را باید وارون کنیم. وارون کردن نیز به معنی تعویض جای صورت و مخرج است. حال سؤال اینجاست که صورت و مخرج عدد $$5$$ چیست؟‌ می‌دانیم که هر عدد برابر با خود عدد تقسیم بر $$1$$ است. بنابراین، عدد $$5$$ در حقیقت همان $$\frac { 5 } { 1 }$$ است. وارون آن نیز با تعویض جای صورت و مخرج به دست می‌آید:

$$\large \frac { 1 } { 5 }$$

حال که عدد پایه را معکوس یا وارون کردیم، وقت آن رسیده که توان را مثبت کنیم:

$$\large (\frac { 1 } { 5 } ) ^ 3$$

اما طبق قاعده ۵ که در ابتدای آموزش به آن اشاره کردیم، داریم:

$$\large (\frac { 1 } { 5 } ) ^ 3 = \frac { 1^3 }{5 ^ 3}$$

همان‌طور که می‌دانیم، عدد $$1$$ به هر توانی برسد (به جز صفر) برابر با $$1$$ است و در نهایت، داریم:

$$\large 5 ^ { - 3 }  = \frac { 1 } { 5 ^ 3 }$$

بنابراین، طبق آنچه گفتیم، توان‌های منفی را می‌توانیم با وارون پایه و توان مثبت نمایش دهیم. برای مثال، داریم:

$$\large 2 ^ {-3} = \frac {1} { 2 ^ 3 } = \frac {1} {(2)(2)(2) }$$

هرچه توان منفی بزرگ‌تر باشد، عدد کوچک‌تر می‌شود. البته در این‌جا، منظور اعداد با پایه بزرگ‌تر از ۱ است. برای مثال، عدد $$2 ^ {-3}$$ بزرگ‌تر از $$2 ^ { - 6 }$$ است.

چگونه اعداد با توان منفی را ساده کنیم؟

پرسشی که اغلب پیش می‌آید، این است که یک عدد با توان منفی را چگونه ساده کنیم و به صورت یک عدد بدون توان بنویسیم. کار ساده است. ابتدا وارون را نوشته و سپس مخرج آن را محاسبه می‌کنیم. سپس با تقسیم صورت بر مخرج، عدد اعشاری مورد نظر را به دست می‌آوریم.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

برای مثال، داریم:

$$\large \begin {align*} 2 ^ { - 4 } & = \frac { 1 } { 2 ^ {4} } \\ \frac { 1 } { 2 ^ 4 } & = \frac { 1 } { 2 \times 2 \times 2 \times 2 } = \frac { 1 } { 1 6 } \\ \frac { 1 } { 16 } & = 0. 0 625 \\ 2 ^ { - 4 } & = 0. 0 625 \end {align*}$$

ضرب اعداد با توان منفی

ضرب توان منفی دقیقاً‌ از همان قوانین توان‌های مثبت پیروی می‌کند. بدین گونه که اگر پایه اعداد یکسان باشد، هنگام ضرب دو عدد، توان‌های آن‌ها را با هم جمع می‌کنیم. در اینجا نیز همین‌گونه است، با این تفاوت که در اینجا با توان منفی نیز سر و کار داریم. مثال زیر، به خوبی این موضوع را نشان می‌دهد.

$$\large 4 ^ 5 \times 4 ^ {-3} = 4 ^ {5+(-3)}=4 ^ 2$$

حالت دیگری نیز وجود دارد که توان‌ها با هم برابر باشند. در این حالت، پایه‌ها را در هم ضرب کرده و توان را بدون تغییر می‌گذاریم. مثال زیر این مطلب را روشن می‌کند:

$$\large 7 ^ { - 5 } \times 6 ^ { - 5 } = (7 \times 6)^ {-5} = 42 ^ { - 5 }$$

اما اگر نه پایه و نه توان با یکدیگر مشابه باشند، باید تک‌تک اعداد را به صورت جداگانه محاسبه کرده و سپس آن‌ها را در هم ضرب کنیم:

$$\large 3 ^ {- 2} \times 2 ^ { - 3 } = \frac { 1 } { 3 ^ 2 } \times \frac { 1 } { 2^ 3 } = \frac { 1 } { 9} \times \frac { 1 } { 8 } = \frac { 1 } {72 }$$

تقسیم اعداد با توان منفی

تقسیم اعداد با توان منفی مشابه ضرب آن‌ها است، با این تفاوت که در این حالت، به جای جمع توان‌ها، آن‌ها را از هم کم می‌کنیم. مثال زیر، این موضوع را به خوبی نشان می‌دهد:

$$\large 3 ^ { - 4 } \div 3 ^{ - 2} = 3 ^ {(-4) - (-2)}= 3 ^ { - 2 }$$

$$\large 3 ^ { - 2 } = \frac { 1 } { 3 ^ 2 }$$

اما اگر پایه‌ها مشابه نبوده و توان‌ها یکسان باشند، پایه‌ها را بر هم تقسیم کرده و توان را تغییر نمی‌دهیم. مثال زیر نشان دهنده این موضوع است:

$$\large 8 ^ { - 4 } \div 2 ^ { - 4 } =(\frac { 8 } { 2 } )^{-4} = 4 ^ { - 4 }$$

$$\large 4 ^ { - 4 } = \frac { 1 } { 4 ^ 4 }$$

اگر مبنا و توان، هر دو مشابهت نداشته باشند، به صورت مستقیم حاصل تقسیم را به دست می‌آوریم:

$$\large 6 ^ { - 2 } \div 3 ^ { - 3 } = \frac { 1 } {6 ^ 2 } \div \frac { 1 } { 3 ^ 3 } = \frac { 1 } { 36} \times \frac { 27 } { 1 } = \frac { 27 } { 36 } = { 3 } { 4} = 0.75$$

توان منفی اعداد منفی

اما اگر مبنای عدد خود منفی باشد، چگونه باید آن را محاسبه کنیم؟‌ همان‌طور که می‌دانیم، برای توان‌های مثبت دو حالت زیر را داریم:

• اگر پایه منفی بوده و توان عدد زوجی باشد، حاصل یک عدد مثبت خواهد بود.
• اگر پایه منفی و توان عددی فرد باشد، آنگاه عدد نهایی نیز یک عدد منفی خواهد بود.

هنگام محاسبه اعدادی با پایه منفی، به نحوه نوشتن آن‌ها دقت کنید. برای مثال، وقتی عدد با علامت منفی درون پرانتز باشد، باید توان را به همان عدد منفی اعمال کنیم. اما برای مثال اگر پرانتزی نداشته باشیم، ابتدا توان را به عدد اعمال کرده و در آخر منفی را اعمال می‌کنیم. مثال‌های زیر، محاسبات در این حالت‌ها را به خوبی نشان می‌دهد:

$$( - 2 ) ^ { - 2 } = \frac { 1 }{ ( - 2 ) ^ { 2 } } = \frac { 1 }{ 4 }$$

$$( - 2 ) ^ { - 3 } = \frac { 1 }{ ( - 2 ) ^ { 3 } } = \frac { 1 }{ - 8 } = - \frac { 1 } { 8 }$$

توان منفی اعداد کسری

برای ساده‌سازی اعداد کسری با توان منفی، همان مراحلی را که گفتیم طی می‌کنیم. کافی است پایه را وارون کرده و توان را مثبت کنیم. مثال زیر، روش انجام این کار را به خوبی نشان می‌دهد:

$$\large (\frac { 2} { 3 }) ^ { - 2 } = (\frac {3 } { 2 }) ^ 2$$

چندجمله‌ای با توان منفی

درک اعداد با توان منفی و ضرب و تقسیم بین آن‌ها گام اول در ساده‌سازی عبارت‌هایی با توان منفی است.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

از یک مثال ساده شروع می‌کنیم. جمله زیر را با توان منفی متغیر $$x$$ در نظر بگیرید که به صورت زیر ساده شده است:

$$\large 4 x ^ { - 3} = 4 \times (\frac { 1 } { x } )^ 3 = \frac { 4 } { x ^ 3 }$$

در این مثال، توان فقط به پایه $$x$$ اعمال شده و تأثیری روی عدد $$4$$ ندارد. برای آنکه عبارت بالا را برحسب توان مثبت بنویسیم، $$x$$ را وارون کرده و توان آن را مثبت می‌کنیم. مثال زیر نیز مربوط به ضرب دو تک‌جمله‌ای است:

$$\large 6 x ^ { - 3 } \times 4 x ^ 5 = \frac { 6 } { x ^ { 3 } } \times 4 x ^ 5 = \frac { 6 \times 4 x ^ 5 } {x ^ 3 } =24 ( x ^ 5 - x ^ 3 ) = 24 x ^ 2$$

در اینجا، متغیر $$x$$ بین دو جمله مشترک است. به همین دلیل توان‌های آن‌ها را با هم جمع جبری می‌کنیم. ضرب اعداد $$4$$ و $$6$$ نیز برابر با $$24$$ است که در نتیجه نهایی مشاهده می‌شود.

اما تقسیم جملات با توان منفی چگونه است؟ مثال ساده زیر را در نظر بگیرید:‌

$$\large \frac { 6 x ^ 3 } { x ^ { - 2 }} = 6 x ^ 3 x ^ 2 = 6 x ^ 5$$

برای مثبت کردن توان منفی متغیر، $$x$$ را بالا می‌آوریم و توان آن را به مثبت تغییر می‌دهیم. در نهایت نیز، به دلیل یکسان بودن مبناها، توان‌ها را با هم جمع می‌کنیم.

اما اگر تعداد متغیرها بیش از یکی باشد، باید چه‌کار کنیم؟ مثال زیر را در نظر بگیرید:

$$\large \frac { 6 x ^ { - 4 }} { y ^ 2 }$$

از آنجا که توان منفی فقط به متغیر $$x$$ اعمال شده است، عبارت $$x ^ { - 4 }$$ را به مخرج کسر می‌آوریم و توان آن را مثبت می‌کنیم. در نتیجه، خواهیم داشت:

$$\large \frac { 6 } { x ^ 4 y ^ 2 }$$

مثال‌ها

در این بخش، چند مثال متنوع را درباره محاسبه اعداد با توان منفی بررسی می‌کنیم.

مثال ۱

عدد $$[ - (-4 ) ^ { - 2 } ] ^ { - 4 }$$ را ساده کنید.

حل: ابتدا حاصل $$(-4)^{-2}$$ را محاسبه می‌کنیم:

$$\large ( - 4 ) ^ { - 2 } = \frac { 1 } {(-4)^ 2 } = \frac { 1} { (-4 ) \times (-4)} = \frac { 1 } { 1 6 }$$

اکنون باید $$[- \frac { 1 } { 16} ] ^ {-4}$$ را به دست آوریم:

$$\large [ - \frac { 1 } { 16} ] ^ {-4} = [- \frac {16}{1}]^ 4 = (-16) ^4 = 16^{4}$$

مثال ۲

عبارت $$( \frac { 12 } { 8 } ) ^ 5 \times ( \frac { 4 }{16} ) ^ { - 5 }$$ را به صورت یک عدد توان‌دار بنویسید.

حل: ابتدا دو عبارت را ساده می‌کنیم:

$$\large ( \frac { 12 } { 8 } ) ^ 5 = (\frac { 2 ^ 2 \times 3 }{2 ^ 3 }) ^ 5 = (\frac {3}{2 })^ 5$$

$$\large ( \frac { 4 }{16} ) ^ { - 5 } = (\frac { 2 ^ 2} { 2 ^ 4})^ {-5} = ( \frac {1}{2 ^ 2 })^ { - 5 }= (2 ^ 2)^ 5 = 2 ^ {10}$$

بنابراین، داریم:

$$\large \begin {align*} (\frac {3}{2}) ^ 5 \times 2 ^ {10} & = \frac {3 ^ 5} {2 ^ 5} \times 2 ^ {10} = 3 ^ 5 \times 2 ^{10-5} \\ & = 3 ^ 5 \times 2 ^ 5 = ({3 \times 2 })^ 5 = 6 ^ 5 \end {align*}$$

مثال ۳

عبارت زیر را ساده کنید:‌

$$\large \frac { 25 ^ {-2 }\times 2 ^ { - 6 } } {2 ^ { - 7 } \times 5 ^ { - 4 } }$$

حل:‌ با توجه به آنچه گفتیم، این عبارت به صورت زیر ساده می‌شود:

$$\large \frac {(5 ^ 2)^ {-2 } \times 2 ^ { – 6 }} {2 ^ { – 7 } \times 5 ^ { – 4 } } = \large \frac {5^ {-4} \times 2 ^ { – 6 }} {2 ^ { – 7 } \times 5 ^ { – 4 } } = \large \frac { 2 ^ { – 6 }} {2 ^ { – 7 } } = { 2 ^ {-6- (-7)} } = 2$$

مثال ۴

عبارت زیر را ساده کنید:

$$\large ( 3 x ^ { - 4 } ) ^ 4 x ^ { - 2 }$$

حل: این عبارت به صورت زیر ساده می‌شود:

$$\large ( 3 x ^ { - 4 } ) ^ 4 x ^ { - 2 } = 3 ^ 4 x ^ { - 1 6 } x ^ { - 2 } = 81 x ^ {-18} = \frac { 8 1 } { x ^ { 1 8 } }$$

آزمون سنجش یادگیری توان منفی

در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث توان منفی را با طرح سوال‌های چندگزینه‌ای می‌سنجیم. پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.