تابع معکوس مثلثاتی — به زبان ساده

پیش‌تر در وبلاگ فرادرس مفاهیم مربوط به توابع مثلثاتی و معکوس توابع را توضیح دادیم. در این مطلب قصد داریم تا در مورد نوعی خاص از توابع معکوس صحبت کنیم. این توابع را توابع معکوس مثلثاتی یا توابع آرک می‌نامند.

پیشنهاد می‌شود به منظور تسلط بهتر به مطلب، مطالب دایره مثلثاتی، سینوس، کسینوس و تانژانت و تابع معکوس مطالعه شوند.

مفهوم توابع معکوس مثلثاتی

همان‌طور که پیش‌تر نیز بیان شد، سینوس، کسینوس و تانژانت زاویه، مفاهیمی هستند که با استفاده از آن‌ها می‌توان بین طول و زوایای یک مثلث ارتباط برقرار کرد. در ابتدا شکل زیر را در نظر بگیرید.

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

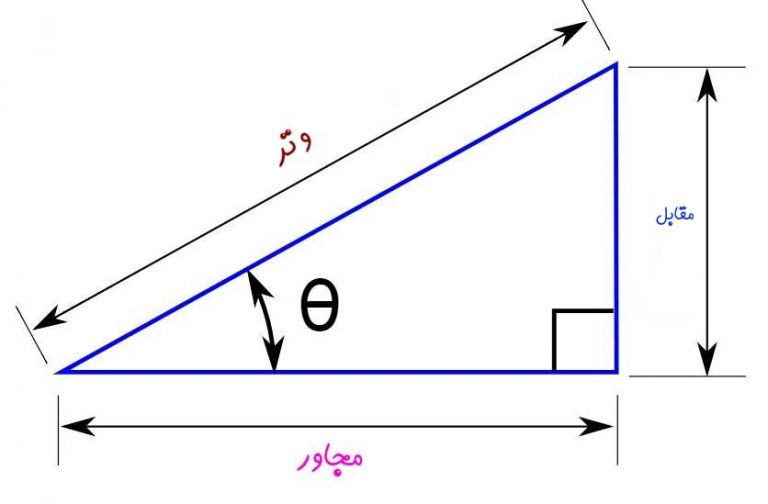
با توجه به شکل فوق، مقادیر مثلثاتی به صورت زیر تعریف می‌شوند:

بنابراین یک زاویه در سینوس یا کسینوس قرار داده شده و خروجی آن محاسبه می‌شود. حال اگر مقدار خروجی را داشته باشیم با استفاده از تابع سینوس معکوس یا آرک سینوس، مقدار زاویه‌ی متناسب با آن بدست می‌آید.

بنابراین تابع $$\large \sin \theta$$ ورودیِ $$\large \theta$$ را گرفته و خروجی آن نسبت طول اضلاع می‌شود. حال تابع $$\large \sin ^ { - 1 }$$ خروجی را می‌گیرد و به ما زاویه می‌دهد.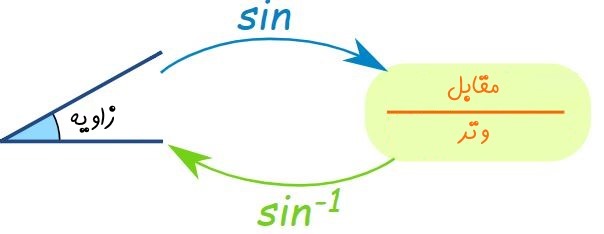

مثال ۱

مقدار $$\large \sin ^ { - 1 } ( 0 . 5 7 )$$ را بیابید.

برای بدست آوردن این مقدار، باید نگاه کنیم و ببینیم سینوس چه زاویه‌ای برابر با ۰.۵۷ می‌شود. با استفاده از ماشین حساب می‌توان دید سینوس زاویه ۳۵ درجه برابر با ۰.۵۷ است. بنابراین می‌توان گفت:

$$\large \sin ^ { - 1 } ( 0 . 57 ) = 3 5 ^ o$$

توجه داشته باشید که توابع معکوس مثلثاتی را ممکن است به صورت آرک نیز نشان دهند.

فیلم آموزش توابع مختلط Complex Functions در فرادرس

کلیک کنید

در ادامه این شکل از تابع معکوس نشان داده شده است.

$$\large \begin {align*} { \cos ^ { - 1 } } \left ( x \right ) & = \arccos \left ( x \right ) \\ { \sin ^ { - 1 } } \left ( x \right ) & = \arcsin \left ( x \right ) \\ { \tan ^ { - 1 } } \left ( x \right ) & = \arctan \left ( x \right ) \end {align*}$$
رابطه ۱

احتمالا تاکنون متوجه شده‌اید که بیان‌های زیر معادل یکدیگر هستند.

$$\large \begin {align*} \theta & = { \cos ^ { - 1 } } \left ( x \right ) & \hspace {0.5in} & \Leftrightarrow & \hspace {0.5in} x & = \cos \left ( \theta \right ) \\ \theta & = { \sin ^ { - 1 } } \left ( x \right ) & \hspace {0.5in} & \Leftrightarrow & \hspace {0.5in} x & = \sin \left ( \theta \right) \\ \theta & = { \tan ^ { - 1 } } \left ( x \right ) & \hspace {0.5in} & \Leftrightarrow & \hspace {0.5in} x & = \tan \left ( \theta \right ) \end {align*}$$

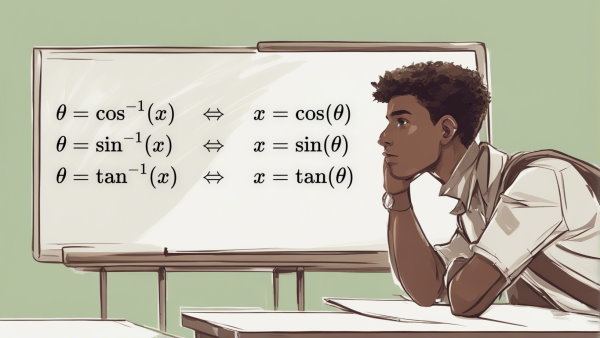
مثال ۲

مقدار معکوسِ $$\large \displaystyle { \cos ^ { - 1 } } \left ( { \frac { { \sqrt 3 } } { 2 } } \right )$$ را بدست آورید.

همان‌طور که در بالا نیز بیان شد، باید از خود بپرسید کسینوس چه زاویه‌ای برابر با $$\large \frac { \sqrt { 3 } } { 2 }$$ می‌شود؟ از مفاهیم پایه‌ای سینوس، کسینوس و تانژانت می‌دانید که کسینوس دو زاویه $$\large 3 0 ^ o$$ ($$\large \frac { \pi } { 6 }$$) و $$\large 330 ^ { \small O }$$ ($$\large \frac { 11 \pi } { 6 }$$) برابر با $$\large \frac { \sqrt { 3 } } { 2 }$$ می‌شود. بنابراین داریم:

$$\large \displaystyle { \cos ^ { - 1 } } \left ( { \frac { { \sqrt 3 } } { 2 } } \right ) = \frac { \pi } { 6 } \ , \ \frac { 11 \pi } { 6 }$$

بدیهی است که اگر یک زاویه را به اندازه ضرایب ۲π دور بزنیم، به نقطه ابتدایی خواهیم رسید. بنابراین پاسخ‌ها را می‌توان به صورت زیر بیان کرد:

$$\large \begin {align*} & \frac { \pi } { 6 } + 2 \pi \, n\, ,\;\;n = 0,\, \pm 1,\, \pm 2,\, \pm 3,\, \ldots \\ & \frac{{11\pi }}{6} + 2\pi \,n\,,\;\;n = 0,\, \pm 1,\, \pm 2,\, \pm 3,\, \ldots \end {align*}$$

توجه داشته باشید ممکن است در صورت سوال محدوده پاسخ بیان شود. برای نمونه اگر پاسخ در بازه ۰ تا π در نظر گرفته شود، نهایتا پاسخ برابر با $$\large \frac { \pi } { 6 }$$ است.

اگر مطلب دایره مثلثاتی را به دقت مطالعه فرموده باشید، می‌توانید معکوس توابع مثلثاتی را راحت‌تر و سریع‌تر محاسبه کنید.

مثال ۳

مقدار $$\large \displaystyle { \cos ^ { - 1 } } \left ( { - \frac { { \sqrt 3 } } { 2 } } \right )$$ را بدست آورید.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

در ابتدا دایره مثلثاتی را به صورت زیر ترسیم کنید.

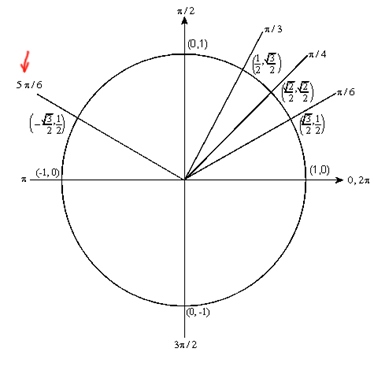
با توجه به دایره، مقدار کسینوس معکوس یا آرک کسینوس برابر می‌شود با:

$$\large { \cos ^ { - 1 } } \left ( { - \frac { { \sqrt 3 } } { 2 } } \right ) = \frac { { 5 \pi } } { 6 }$$

مثال ۴

مقدار $$\displaystyle \cos \left( {{{\cos }^{ - 1}}\left( {\frac{{\sqrt 3 }}{2}} \right)} \right)$$ را بدست آورید.

در مطلب تابع معکوس عنوان شد که اگر یک تابع معکوس را در خودش قرار دهیم، مقدار خروجی برابر با ورودی است. در این حالت نیز از تابع آرک کسینوس، کسینوس گرفته شده. بنابراین مقدار آن برابر است با:

$$\large \cos \left ( { { { \cos } ^ { - 1 } } \left ( { \frac { { \sqrt 3 } } { 2 } } \right ) } \right ) = \cos \left ( { \frac { \pi } { 6 } } \right ) = \frac { { \sqrt 3 } } { 2 }$$

نمودار توابع معکوس مثلثاتی

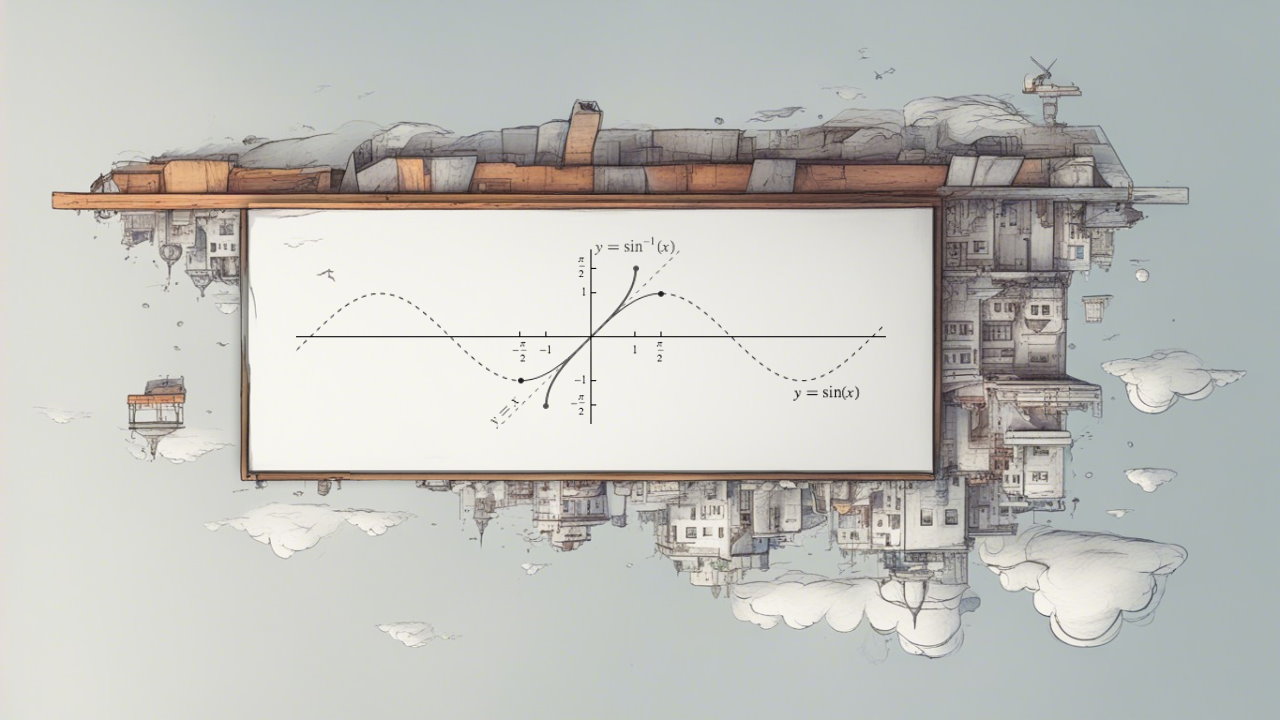
در رابطه ۱ توابع معکوس مثلثاتی ارائه شدند. برای بدست آوردن نمودار توابع معکوس کافی است که آن‌ها را نسبت به محور y=x معکوس کنیم.

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

برای نمونه در شکل زیر نمودار تابع y=cos x نسبت به y=x قرینه شده و تابع y=cos^-1x بدست آمده است.

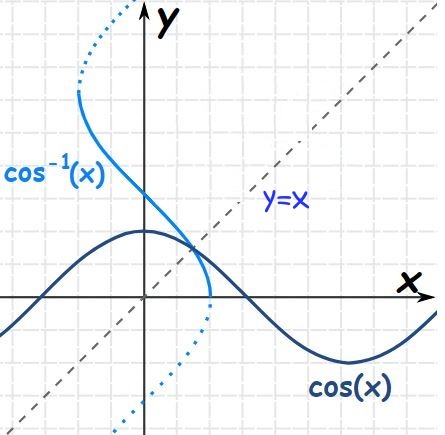
در ادامه نمودار توابع آرک سینوس، کسینوس و تانژانت ارائه شده است.

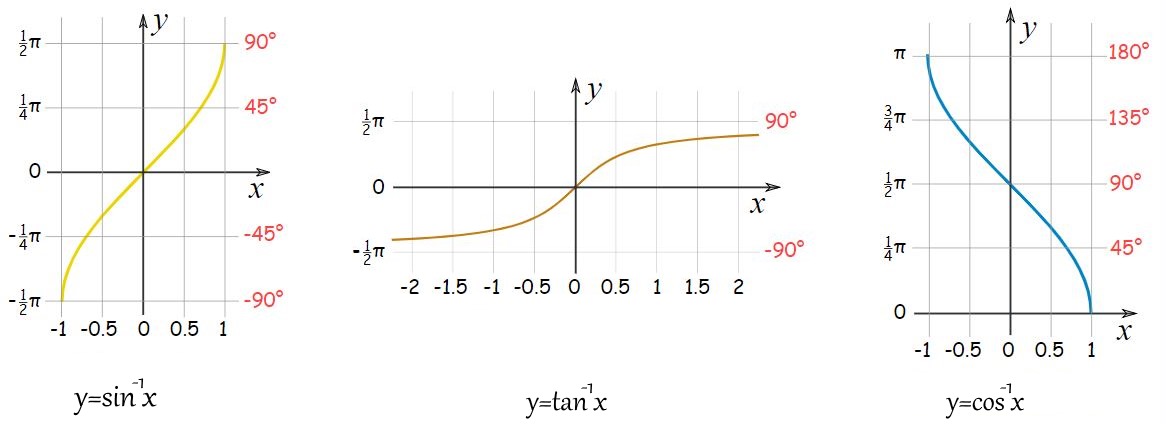
در این مطلب مفاهیم پایه‌ای توابع معکوس مثلثاتی یا توابع آرک توضیح داده شدند. البته در آینده مشتق‌ توابع معکوس مثلثاتی را نیز توضیح خواهیم داد.