تصاعد حسابی – به زبان ساده
در این مطلب قصد داریم تا مفهومی بسیار مهم در ریاضیات، تحت عنوان «تصاعد حسابی» (Arithmetic Sequence) را توضیح دهیم. در ابتدا فرض کنید میخواهید حاصل جمع اعداد ۱ تا ۱۰۰ را بدست آورید.


به نظر شما اگر بخواهید این عمل را دستی -یا حتی با ماشین حساب- انجام دهید، چقدر وقت نیاز خواهید داشت؟ بدیهی است که عمل مذکور بسیار زمانبر خواهد بود؛ اما با استفاده از مفهوم تصاعد حسابی میتوانید این کار را به آسانی و حتی بهصورت ذهنی انجام دهید! در انتهای این مطلب به این سوال پاسخ خواهیم داد. جهت یادگیری تصاعد حسابی در ابتدا نیاز است تا با مفهومِ دنباله آشنا باشید.
دنباله
یک دنباله به مجموعهای از اشیاء (معمولا اعداد) اطلاق شده که در بیشترِ مواقع با نظم مشخصی بیان میشوند.
در زیر نمونهای از یک دنباله نشان داده شده است.
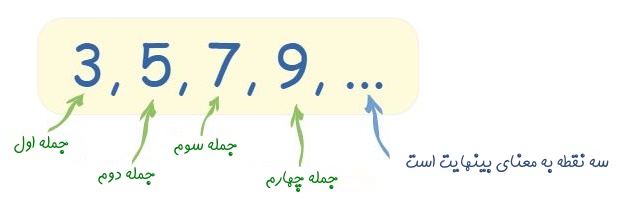
به هرکدام از اعداد ارائه شده در بالا، جمله -یا تِرم- گفته میشود. برای نمونه دنباله فیبوناچی به مجموعهای از اعداد اطلاق میشود که از ویژگیهای شگفتانگیزی برخوردار است.
تصاعد حسابی
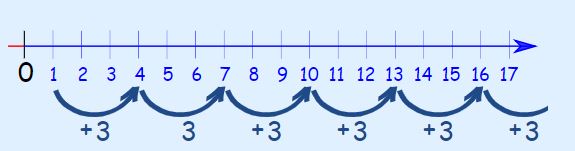
تصاعد حسابی، دنبالهای است که فاصله بین اعداد آن، مقداری ثابت است. برای ساختن دنبالهای حسابی، در ابتدا عددی در نظر گرفته و عدد مشخصی را به آن اضافه کنید. برای نمونه اگر عدد اولیه برابر با ۱ و مقدار ثابت اضافه شده، برابر با ۳ باشد، تصاعد حسابی مرتبط با آن بهصورت زیر در خواهد آمد.

همانطور که در دنباله بالا نیز میبینید هرکدام از جملات به اندازهی ۳ افزایش یافته.
بنابراین یک تصاعد حسابی را میتوان به شکلی عمومی، بهصورت زیر بیان کرد:

اجزاء رابطه بالا برابرند با:
- a: جملهی اول تصاعد
- d: اختلاف میان دو جملهی متوالیِ تصاعد که معمولا آن را تحت عنوان قدرِ نسبت میشناسند.
مثال ۱
ثابتهای a و d را در دنبالهی زیر مشخص کنید.

جملهی اول دنباله بالا برابر با ۱ بوده که همان a محسوب میشود. از طرفی فاصله هر دو جمله از دنباله فوق برابر با ۳ بوده که نشان دهنده d=3 است. در زیر الگوی جملات دنباله مفروض نشان داده شده است.

فرمول عمومی دنباله حسابی
یک دنباله حسابی را میتوان در قالب فرمول زیر بیان کرد:
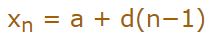
در رابطه فوق a و d بهترتیب نشان دهنده جمله اول و قدرنسبت هستند. همچنین عدد n نشان دهنده شماره جمله است. توجه داشته باشید که دلیل استفاده از n-1 این است که در جمله اول از قدرنسبت استفاده نمیشود.
مثال ۲
رابطه عمومی دنباله زیر را بهدست آورده و جمله نهم را نیز محاسبه کنید.

مطابق با شکل زیر، اختلاف هر دو جمله از سری بالا برابر با ۵ است.
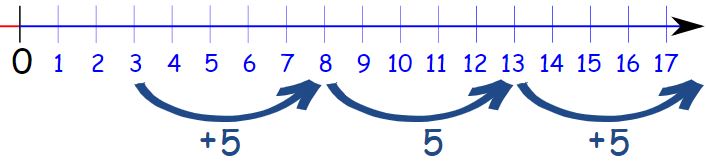
در حقیقت قدر نسبت دنباله فوق برابر با ۵ و جمله اول آن نیز ۳ است. از این رو با استفاده از رابطه ۱ و جایگذاری a و d در آن، رابطه عمومی دنباله فوق بهصورت زیر بدست میآید.
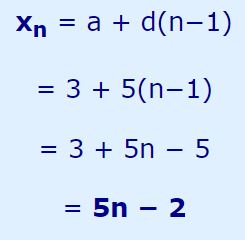
با استفاده از رابطه فوق، جملهی نهم برابر با عدد زیر بدست میآید.
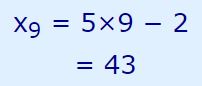
حاصل جمع جملات
یکی از کاربردهای مهم تصاعد حسابی، محاسبه حاصل جمع اعدادی است که شاید محاسبه دستی آنها زمانگیر و سخت باشند.
در ابتدا دنبالهای حسابی را بهصورت زیر در نظر بگیرید.
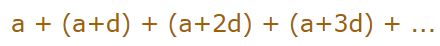
حاصل جمع جملات اول تا nام را میتوان با استفاده از رابطه زیر بدست آورد.
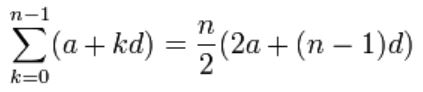
علامت در رابطه بالا نشان دهنده حاصل جمع است. استفاده از این نماد مطابق با الگوی زیر است.
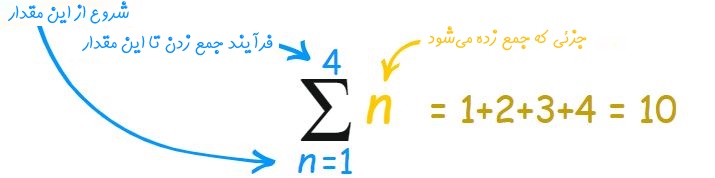
رابطه بالا بهصورت "حاصل جمع n، زمانی که n از ۱ تا ۴ تغییر کند"، خوانده میشود.
مثال ۳
حاصل جمع ۱۰ جملهی اول دنباله زیر را بیابید.

مقادیر d ،a و n برابرند با:
- a=1
- d=3
- n=10
با جایگذاری مقادیر فوق در رابطه ۲ حاصل جمع ۱۰ جمله اول برابر است با:
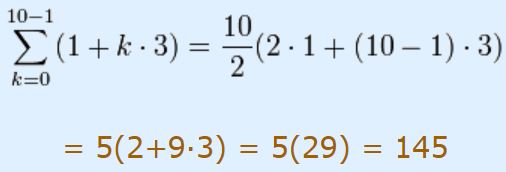
حال قصد داریم تا چالشی را پاسخ دهیم که در ابتدای این مطلب ذکر شد. فرض کنید میخواهید حاصل جمع اعداد ۱ تا ۱۰۰ را بدست آورید. برای انجام این کار دنبالهای را بهصورت زیر تعریف میکنیم:

در دنباله فوق a=1 و d نیز برابر با ۱ است. جهت بدست آوردن حاصل جمع ۱۰۰ جملهی اول، n=100 را در رابطه ۲ قرار داده و حاصل جمع را همانگونه که در زیر نشان داده شده بدست میآوریم.

اثبات فرمول محاسبه حاصل جمع
شاید این سوال در ذهن شما مطرح شده باشد که چرا رابطه ۲ درست کار میکند؟ جهت اثبات رابطه مذکور، جملات دنباله را در دو حالتِ زیر مینویسیم:
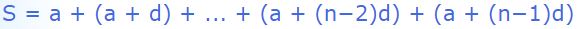
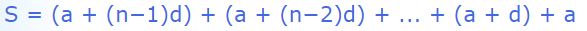
حال طرفین دو رابطه بالا را بهصورت زیر جمع میزنیم.
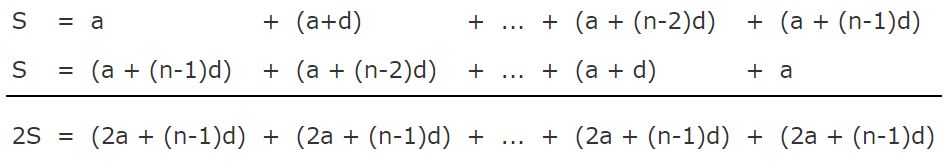
نکته جالب در حاصل جمع بدست آمده در بالا این است که تمامی مقادیرِ 2S با هم برابر هستند. همچنین تعداد این جملات نیز همان n است. در نتیجه حاصل 2S برابر است با:

با تقسیم کردن طرفین رابطه بالا به ۲، مقدار S برابر با عبارت زیر بدست میآید.
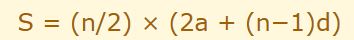
عبارت بالا نیز در حقیقت همان رابطه ۲ را نشان میدهد؛ در نتیجه رابطه مذکور صحیح است. نمونهای دیگر از تصاعد تحت عنوان تصاعد هندسی نیز وجود دارد که در آن هر دو جمله متوالی ضریب ثابتی از یکدیگر هستند. در مطلبی بهصورت مجزا این مفهوم را نیز تشریح خواهیم کرد.













سلام
لازم نیست اینقدر روی خودتون فشار بیارید جمله اول وآخر دنباله رو باهم جمع کنید ضرب در تعداد جملات تقسیم بر دو میشه مجموع جملات .
اون در صورتیه که جمله اول و آخرو داشته باشیم
من فعلا فرصت نکردم با مجموعه ی شما آشنا شم و سایتو خوب بگردم ولی به خیلی از سوالام سریع و مختصر رسیدم . از این بابت خداروشکر میکنم و از شما تشکر میکنم و دعاتون میکنم خداخیرتون بده.
این برای n جمله ی اول بود اگه مجموع حمله پنج و سیزدع رو بخاد چی مثلا سوال میگ مجموع7+8+12میشه 32مجموع جملات5+13چند میشه
سلام. مقاله عالی بود. ولی k رو متوجه نشدم. فکر کنم به عنوان جملههای دنباله بود؟ همه چیز رو فهمیدم ولی اگر این رو توضیح بدید ممنون میشم ✋?
سلام.
k در این مثال خاص، اعداد 0 تا n−1 را شامل میشود و بهصورت زیر در یک دنباله عددی به کار رفته است:
k=0k=1k=2⋮k=n−1:a:a+d:a+2d⋮:a+(n−1)d
دقت کنید که k جمله این دنباله نیست و متغیری است که مقادیر مختلفی را برای هر جمله این دنباله به خود میگیرد.
موفق باشید.
میشه توضیح بدین k چیه اصن؟
سلام تعداد ۹واسطه حسابی بین ۰و۵ درج کنید به طوری که جمله اول دنباله حسابی ایجاد شده صفر باشد
سلام
میشه بفرمائید جمله عمومی دنباله 0,2,7,15,23,100 چیست ؟
سلام
میتونید فرمول عددی این دنباله را پیدا کنید ؟
…و100و23و15و7و2و0
قدر نسبت تصاعد d در دنباله حسابي ميتونه صفر باشد ؟
اره
مثل دنباله ی حسابی ۲،۲،۲،۲،۲
نمیشه اینو به صورت پی دی اف سیو کنم؟
برا کنفرانس احتیاج دارم بهش
سلام
مجموع ۱۵ جمله ی اول دنباله ی حسابی زیر را بدست اورید.
…,۱,۶,۱۱,۱۶
چطور بدست میاد?
درود بر شما
فرض کنید هر ماه به طور منظم 100 تومان به حساب بانکی ام اضافه میکنم. حال اینکه بانک به موجودی حساب هر ماه، 10 درصد ماهیانه (بطور مثال) سود میدهد. فرمول محاسبه میزان پول من پس از n ماه چقدر است. ممنون
سلام و درود بر شما خواننده گرامی،
سوال شما در مورد رشد و یا صحیح تر نرخ رشد است. پیشنهاد میشود برای پیدا کردن پاسخ خود به متن نوشتار فرمول نرخ رشد در اکسل — آموزش محاسبه به زبان ساده یا مفهوم نرخ رشد مرکب سالانه و روش محاسبه آن — به زبان ساده مراجعه کنید. توجه داشته باشید که در تصاعد حسابی، میزان افزایش ثابت است در حالیکه در تصاعد هندسی نرخ رشد ثابت است.
تندرست و پیروز باشید.
سلام
لطفا بفرماییدجمله عمومی دنباله ( ……-111111-11111-1111-111-11-1-0) چیست؟
سلام و روز بخیر،
از اینکه همراه مجله فرادرس هستید بسیار خرسنیدم.
اگر منظورتان از خط تیر (-) فاصله بین جملهها باشد میتوانیم عبارت یا جمله عمومی دنباله را به صورت زیر بنویسیم
xi+10i−1
به این ترتیب به ازای i = 0، مقدار x0=0 بدست می آید. x1=1 , x2=1+10=11, x3=11+100=111, x4= 111+1000 = 1111
تندرست و پاینده باشید.
mrc vaghean. sare class gij shode boodam vali alan ghashang fahmidam?
سلام. اگر قدر نسبت ثابت نباشد ، چطور می توان جمله عمومی نوشت؟
مثلا
۱،۳،۶،۱۰،۱۵
این یه دنباله درجه دومه
به صورت : یک دوم n به توان 2 + یک دوم n
سلام
خیلی خوب توضیح داده بودین من تومدرسه اصلاً یاد نگرفته بودم ولی قسمت دوم که k وارد قضیه شد را متوجه نشدم. نگفتین که K توی فورمول کجا رفت یا معرف چیه و…!
بسیار بسیار عالی