امپدانس ذاتی محیط — به زبان ساده

امواج الکترومغناطیسی به هنگام انتشار در یک محیط (خلأ، هوا یا هر نوع ماده‌ای) با مقاومتی موسوم به امپدانس ذاتی مواجه می‌شوند. امپدانس ذاتی همانند مقاومت یا امپدانس یک مدار یا خطوط انتقال، با واحد «اهم» (Ohm : Ω) سنجیده می‌شود. در مقوله انتشار امواج الکترومغناطیسی امپدانس را غالباً با عناوینی مانند امپدانس ذاتی محیط یا امپدانس موج مورد خطاب قرار می‌دهند و بیانگر نسبت میدان الکتریکی به میدان مغناطیسی موج ($$\frac{E}{H}$$) است. از آنجایی که در سیستم بین‌المللی $$SI$$، واحد $$E$$ و $$H$$ به ترتیب ($$\frac{V}{m}$$) و ($$\frac{A}{m}$$) است، پس واحد نسبت ($$\frac{E}{H}$$) برابر با ($$\frac{V}{A}$$) شده که خود مطابق با قانون اهم، تعریف واحد اهم (Ω) است.

در ادامه این مقاله با ما همراه باشید تا با زبانی ساده به بررسی امپدانس ذاتی محیط و عوامل موثر در آن بپردازیم.

معادلات ماکسول

در مقاله «معادلات ماکسول (Maxwell’s Equations) — به زبان ساده» با معادلات ماکسول به طور کامل آشنا شدیم. دیدیم که جهت بررسی و تحلیل پدیده‌های الکتریکی و مغناطیسی و به طور کل تحلیل الکترومغناطیسی، می‌توان از این ۴ معادله که به شرح ذیل هستند، استفاده کرد:

$$\large \triangledown.D=\rho$$
(1)

$$\large \triangledown.B=0$$
(2)

$$\large \triangledown \times E=-\frac{\partial B}{\partial t}$$
(3)

$$\large \triangledown \times H=\frac{\partial D}{\partial t}+J$$
(4)

فیلم آموزش الکترومغناطیس مهندسی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

در معادلات فوق $$D$$ جا‌به‌جایی الکتریکی، $$\rho$$ چگالی بار، $$B$$ چگالی شار مغناطیسی، $$H$$ شدت میدان مغناطیسی، $$E$$ شدت میدان الکتریکی و $$J$$ چگالی جریان الکتریکی است.

معادلات مذکور در محیطی همسانگرد (Isotropic)، همگن (Homogeneous)، نارسانا (Nonconducting) و بدون بار (Uncharged) نظیر شیشه به شکل زیر در می‌آیند:

$$\large \epsilon \triangledown.D=0$$
(5)

$$\large \mu \triangledown.H=0$$
(6)

$$\large \triangledown \times E=-\mu \frac{\partial H}{\partial t}$$
(7)

$$\large \triangledown \times H=\epsilon \frac{\partial E}{\partial t}$$
(8)

اگر عبارات توصیفی بالا برای محیط شرطی برایتان نامفهوم است، تعاریف زیر را به خاطر بسپارید:

• محیط همگن: محیطی را همگن می‌گویند که در آن میدان الکتریکی $$E$$ و قطبش $$P$$ وابسته به مکان نباشند.
• محیط همسانگرد: محیطی را همسانگرد می‌گویند که در آن بردار قطبش $$P$$ به جهت بردار $$E$$ وابسته نباشد. به عبارت دیگر، دو بردار موازی باشند.

همچنین در مقاله «معادله موج — از صفر تا صد» دیدیم که از معادلات ماکسول می‌توان به معادله موج برای مولفه‌های الکتریکی و مغناطیسی رسید. با گرفتن کرل ($$\triangledown \times$$) از طرفین معادله (7) و استفاده از سایر معادلات جهت حذف $$H$$ به معادله موج الکتریکی زیر می‌رسیم:

$$\large \triangledown^{2} E=\epsilon \mu \frac{\partial{^2}E}{\partial t^{2}}$$
(9)

سرعت موج

عبارت ($$\epsilon \mu$$) در معادله (9)، مرتبط به سرعت موج در محیط است که از طریق فرمول زیر بیان می‌شود:

$$v^{2}=\frac{1}{\epsilon\mu}$$
(10)

فیلم آموزش امواج و ارتعاشات (رایگان) در فرادرس

کلیک کنید

اگر معادله موج (9) را در محیط خلأ بنویسیم، عبارت $$\epsilon \mu$$ به فرم $$\epsilon_{0} \mu_{0}$$ در آمده که به سرعت موج الکترومغناطیسی در خلأ ارتباط دارد. با جایگذاری مقدار عددی ضریب نفوذپذیری الکتریکی $$\epsilon_{0}$$ و ضریب نفوذپذیری (تراوایی) مغناطیسی $$\mu_{0}$$، مطابق با انتظار، این سرعت برابر با سرعت نور می‌شود.

$$c=\frac{1}{\sqrt{\epsilon_{0}\mu_{0}}}=3\times 10^{8} \ \frac{m}{s}$$
(11)

در مقاله «ضریب شکست و محاسبه عملی آن -- به زبان ساده» دیدیم که سرعت نور یا به طور جامع‌تر سرعت امواج الکترومغناطیسی در یک محیط، به صورت زیر تعریف می‌شود:

$$v=\frac{c}{n}$$
(12)

حال از رابطه فوق و (10)، می‌توانیم نسبت سرعت موج در دو محیط مختلف را به شکل زیر بنویسیم:

$$\frac{v_{1}}{v_{2}}=\frac{n_{2}}{n_{1}}=\sqrt{\frac{\epsilon_{2}\mu_{2}}{\epsilon_{1}\mu_{1}}}$$
(13)

در صورتی که دو محیط (ماده) مغناطیسی نباشند، می‌توان ضریب نفوذپذیری (تراوایی) مغناطیسی را برای هر دو محیط $$\mu=\mu_{0}$$ در نظر گرفت. در نتیجه:

$$\frac{v_{1}}{v_{2}}=\frac{n_{2}}{n_{1}}=\sqrt{\frac{\epsilon_{2}}{\epsilon_{1}}}$$
(14)

نتیجه جالب توجهی که می‌توان از رابطه فوق گرفت، رسیدن به رابطه‌ای جهت محاسبه ضریب شکست محیط است. در واقع اگر محیط $$n_{1}$$ را خلأ فرض کنیم، $$\epsilon_{1}\equiv\epsilon_{0}$$ شده و در نتیجه:

$$n=\sqrt{\frac{\epsilon}{\epsilon_{0}}}$$
(15)

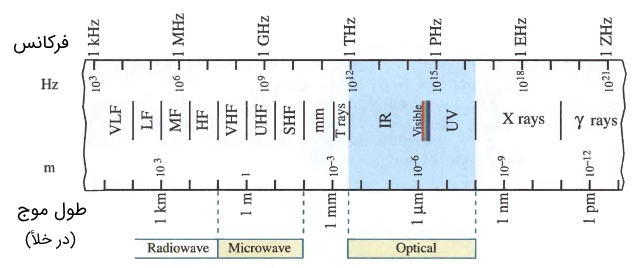
برای امواج الکترومغناطیسی فرکانس بالا (نظیر نور) که در یک محیطی دی‌الکتریک حرکت می‌کنند، بردار جابه‌جایی الکتریکی ($$D$$) ناشی از قطبش محیط (القا دوقطبی‌ها) نمی‌تواند همگام با میدان الکتریکی $$E$$ تغییر کند و لذا از آن عقب می‌ماند. در این حالت رابطه (15) شکل پیچیده‌تری به خود گرفته و به صورت عددی مختلط نمایش داده می‌شود که عامل فرکانس و طول موج را در دل خود دارد. به عبارتی ضریب شکست یک محیط تابعی از طول موج یا فرکانس موجی است که در آن منتشر می‌شود. پرداختن به رابطه ضریب شکست مختلط خارج از هدف این مقاله است. جهت آشنایی با محدوده فرکانسی امواج الکترومغناطیسی به مقاله «طیف الکترومغناطیسی -- به زبان ساده» مراجعه کنید. همچنین جهت آشنایی با پدیده قطبش در مواد، به مقاله «دی‌الکتریک -- به زبان ساده» رجوع کنید.

حال اگر از طرفین رابطه (8)، کرل گرفته و مولفه $$E$$ را حذف کنیم، به معادله موج مغناطیسی زیر می‌رسیم.

$$\large \triangledown^{2} H=\epsilon \mu \frac{\partial{^2}H}{\partial t^{2}}$$
(16)

نتایجی که برای سرعت انتشار موج و ضریب شکست در فوق حاصل شد، از رابطه (16) نیز قابل حصول هستند.

امپدانس ذاتی محیط یا امپدانس موج (Wave Impedance)

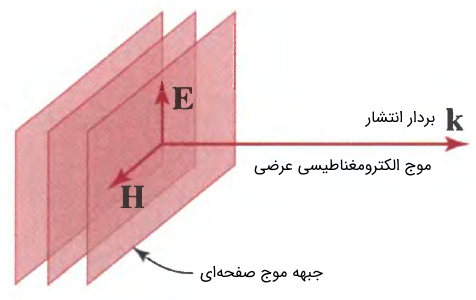
با پیش گرفتن رویکرد خطی در امواج صفحه‌ای الکترومغناطیسی عرضی (Transverse Electro Magnetic : TEM) تک رنگ (تک فرکانس) می‌توانیم دو معادله (7) و (8) را به فرم زیر بنویسیم.

$$k\times E_{0}=\omega\mu H_{0}$$
(17)

$$k\times H_{0}=-\omega\mu E_{0}$$
(18)

از دو رابطه فوق، نسبت اندازه دامنه‌های امواج الکتریکی و مغناطیسی، یعنی $$\frac{E_{0}}{H_{0}}$$ را می‌توان به صورت زیر نوشت ($$k$$ عمود بر $$E$$ و $$H$$ است):

$$H_{0}=(\frac{k}{\omega\mu})E_{0}$$
(19)

$$H_{0}=(\frac{\omega\epsilon}{k})E_{0}$$
(20)

$$\Rightarrow \frac{\omega\epsilon}{k}=\frac{k}{\omega\mu}\rightarrow k^{2}=\omega^{2}\epsilon\mu\rightarrow k=\omega\sqrt{\epsilon\mu}=\frac{\omega}{v}=n\frac{\omega}{c}$$
(21)

$$\Rightarrow \frac{E_{0}}{H_{0}}=\frac{\omega\mu}{k}=c\mu=\sqrt{\frac{\mu}{\epsilon}}$$
(22)

نسبت $$\frac{E_{0}}{H_{0}}$$، به امپدانس ذاتی محیط یا امپدانس مشخصه موسوم است که غالباً با η یا $$Z$$ نمایش داده می‌شود. با نوشتن این نسبت برای موج الکترومغناطیسی که در خلأ منتشر می‌شود، امپدانس ذاتی خلأ به صورت زیر نتیجه می‌شود:

$$\eta_{0}=\frac{E_{0}}{H_{0}}=\sqrt{\frac{\mu_{0}}{\epsilon_{0}}}=120\pi=377 \ Ω$$
(23)

رابطه فوق بیان می‌کند، امواج الکترومغناطیسی که در خلأ منتشر می‌شوند، در مقابل خود مقاومتی حدود 377Ω احساس می‌کنند. از آنجایی که ضریب شکست هوا را با تقریب خوبی می‌توان برابر با ضریب شکست خلأ در نظر گرفت، امپدانس ذاتی هوا نیز همین مقدار است. به عبارت دیگر، هوای بین دو آنتن فرستنده و گیرنده را می‌توان خط انتقالی (نظیر یک سیم) با امپدانس 377 اهم در نظر گرفت. جهت آشنایی با امپدانس مدارهای الکتریکی به مقاله «امپدانس و محاسبه آن -- به زبان ساده» مراجعه کنید.

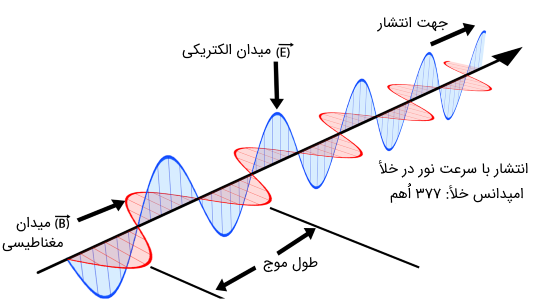
امپدانس ذاتی یک محیط را می‌توان بر حسب ضریب شکست آن محیط به شکل زیر نوشت:

$$\eta=\frac{\eta_{0}}{n}$$
(24)

همچنین شدت موج الکترومغناطیسی بر حسب امپدانس ذاتی (مشخصه) محیط به شکل زیر در می‌آید.

$$I=\frac{|E_{0}|^{2}}{2\eta}$$
(25)

لازم به ذکر است که امپدانس ذاتی یا مشخصه در اینجا به امپدانس موج نیز معروف است. امپدانس موج در حالت کلی‌تر با در نظر گرفتن خواص الکتریکی محیط، به صورت زیر در می‌آید (σ ضریب رسانایی $$J=\sigma E \leftarrow$$):

$$Z=\sqrt{\frac{j\omega\mu}{\sigma+j\omega\epsilon}}$$
(26)

در واقع رابطه (22) نیز خود حالت خاصی از معادله‌ (۲۷) است که در آن دامنه‌های مولفه $$E$$ و $$H$$ هم‌زمان به صفر و مقدار ماکزیمم خود می‌رسند. در این حالت، $$\omega\epsilon \ >> \ \sigma$$ بوده و در نتیجه:

$$Z=\sqrt{\frac{j\omega\mu}{\sigma+j\omega\epsilon}} \ \ \ \ , \ \ \ if \ : \ \omega\epsilon \ >> \ \sigma \ \ \Rightarrow \ Z=\sqrt{\frac{\mu}{\epsilon}}$$
(27)

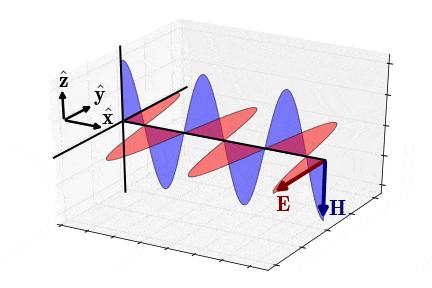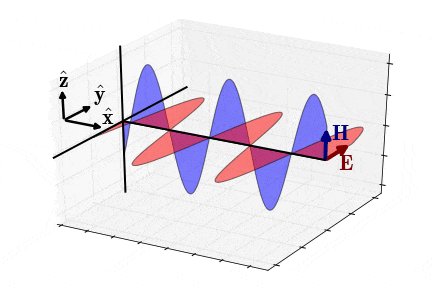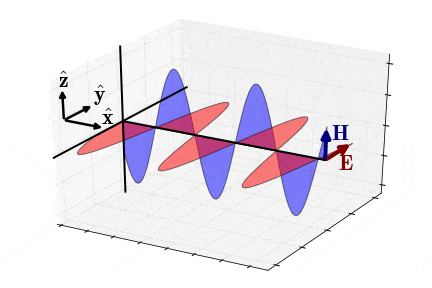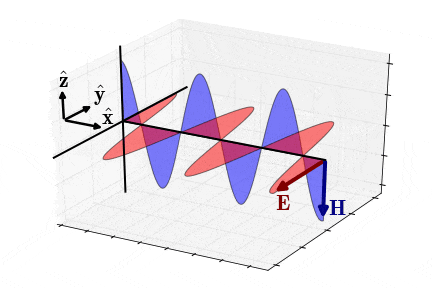
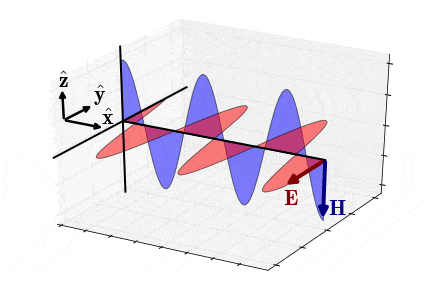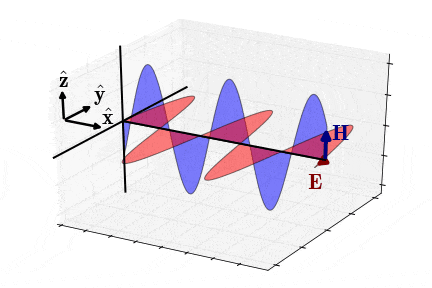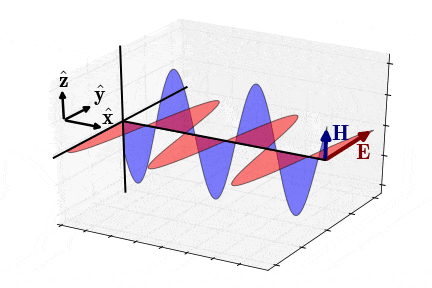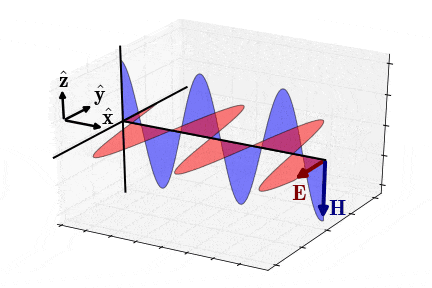
برای حالت شبه‌استاتیک (Quasi-Static Approximation)، یعنی زمانی که مولفه‌های $$E$$ و $$H$$ به اندازه $$\frac{\pi}{4}$$ با یکدیگر اختلاف فاز دارند (شکل 7)، امپدانس موج یا امپدانس ذاتی محیط به شکل زیر در می‌آید ($$\omega\epsilon << \ \sigma$$):

$$Z=\sqrt{\frac{j\omega\mu}{\sigma+j\omega\epsilon}} \ \ \ \ , \ \ \ if \ : \ \omega\epsilon \ << \ \sigma \ \ \Rightarrow \ Z=\sqrt{\frac{j\omega\mu}{\sigma}}=\frac{\omega\mu}{\sqrt{-j\omega\mu\sigma}}$$
(28)

امپدانس موج در محیط دی‌الکتریک

در یک محیط همسانگرد و همگن دی‌الکتریک با ضریب دی‌الکتریک (نفوذپذیری نسبی) $$k\equiv\epsilon_{r}$$، که خاصیت مغناطیسی نیز ندارد ($$\mu=\mu_{0}$$)، امپدانس موج به صورت زیر محاسبه می‌شود:

$$Z=\sqrt{\frac{\mu}{\epsilon}}=\sqrt{\frac{\mu_{0}}{\epsilon_{0}\epsilon_{r}}}=\frac{Z_{0}}{\sqrt{\epsilon_{r}}}=\frac{377}{\sqrt{\epsilon_{r}}} \ Ω$$
(29)

امپدانس موج در موجبر

امواج الکترومغناطیسی که در موجبر‌ها نیز منتشر می‌شوند، در مقابل خود مقاومت یا امپدانس احساس می‌کنند. امپدانس موج برای امواج منتشر شده در داخل موجبرها با هر نوع ساختاری (استوانه‌ای، مستطیلی و ...) به فرکانس موج و فرکانس قطع (cut-off frequency) بستگی دارد. فرکانس قطع، حداقل فرکانسی است که موج جهت انتشار در موجبر باید داشته باشد.

امپدانس موج برای مد عرضی میدان الکتریکی (Transverse Electric : TE) در یک موجبر مستطیلی به صورت زیر تعریف می‌شود.

$$Z_{TE}=\frac{Z_{0}}{\sqrt{1-(\frac{f_{c}}{f}})^{2}}$$
(30)

در رابطه فوق، $$Z_{0}$$ امپدانس ذاتی خلأ با مقدار 377 اهم و $$f_{c}$$ فرکانس قطع موجبر است. همچنین برای مد عرضی میدان مغناطیسی (Transverse Magnetic : TM)، امپدانس موج برای یک موجبر مستطیلی به شکل زیر است:

$$Z_{TM}=Z_{0}\sqrt{1-(\frac{f_{c}}{f}})^{2}$$
(31)

در دو رابطه فوق، اگر فرکانس موج منتشر شده، بیشتر از فرکانس قطع باشد ($$f \ > \ f_{c}$$)، امپدانس موج حقیقی شده و محیط مشابه یک مقاومت است. در این صورت موج حامل انرژی است. در فرکانس‌های زیر فرکانس قطع نیز، امپدانس موهومی (مقاومت واکنشی) است و موج به مرور محو شده (انرژی از دست می‌دهد) و توانایی انتشار در آن موجبر را ندارد. این امر برای انتقال موج در مسیر‌های طولانی حائز اهمیت است.

یک مثال نام آشنا برای مهندسان، امپدانس مرسوم 50 اهم کابل‌های کواکسیال (Coaxial cable) است. در حوزه مخابرات، به خصوص مخابرات فرکانس بالای میکروویو (microwave communication)، از کابل‌های کواکسیال به وفور استفاده می‌شود. همچنین در این حوزه، تطبیق امپدانس خطوط انتقال بحث مهمی است که جهت انتشار مناسب امواج الکترومغناطیسی باید رعایت شود. با این تعریف آنتن را می‌توان وسیله‌ای در نظر گرفت که میان فضای آزاد با امپدانس 377Ω و موجبر استوانه‌ای (کابل کواکسیال) 50Ω عمل تطبیق امپدانس را انجام می‌دهد.

اگر مطالب ارائه شده در این مقاله برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مخابرات فیبر نوری -- به زبان ساده
• فیبر نوری -- به زبان ساده
• امواج رادیویی -- به زبان ساده

^^