تنش سه محوری و مفاهیم مرتبط با آن — به زبان ساده

تنش صفحه‌ای، یکی از حالت‌های دوبعدی تنش است که در آن تمام مؤلفه‌ها بر روی یک صفحه قرار دارند. این نوع تنش هنگامی رخ می‌دهد که یکی از سه تنش اصلی در المان مورد تحلیل برابر با صفر باشد (مانند دیواره مخازن ﺟﺪار ﻧﺎزک یا سیالات تحت فشار). با این وجود، معمولاً مقدار تنش در امتداد هیچ‌یک از سطوح جسم صفر نیست. در این شرایط، حالت تنش با عنوان «تنش سه‌محوری» (Triaxial Stress) شناخته می‌شود. در این مقاله، به معرفی تنش‌های برشی ماکسیمم، قانون هوک، اتساع، چگالی انرژی کرنشی و حالت‌های خاص تنش سه محوری خواهیم پرداخت.

مولفه‌های تنش سه‌محوری

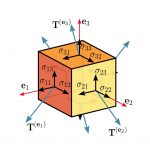
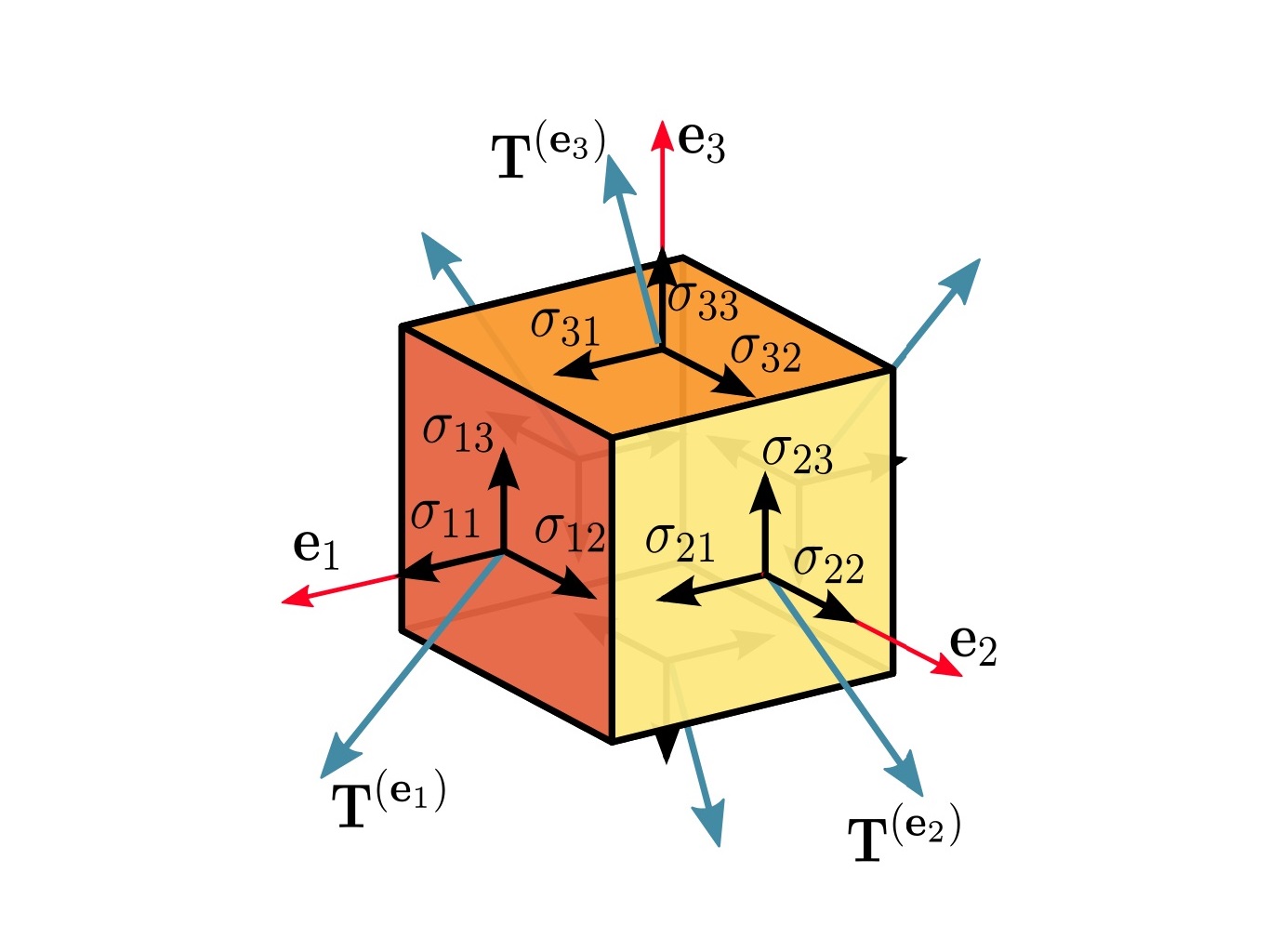
المان زیر در سه راستای عمود بر هم تحت تنش‌های نرمال σ_y ،σ_x و σ_z قرار دارد. به این حالت، تنش سه‌محوری گفته می‌شود. به دلیل عدم وجود تنش‌های برشی در صفحات y ،x و z، مولفه‌های σ_y ،σ_x و σ_z به عنوان تنش‌های اصلی در نظر گرفته می‌شوند.

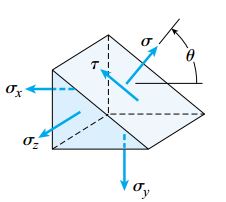
یک صفحه مورب و موازی با محور z را مطابق با شکل زیر در نظر بگیرید. تنش‌های اعمال شده بر روی این صفحه مورب، تنش نرمال σ و تنش برشی τ هستند که جهت‌گیری آن‌ها به موازات صفحه xy است. این تنش‌ها را می‌توان معادل تنش‌های موجود بر روی صفحات دوران‌یافته در نظر گرفت. مقادیر تنش‌های σ و τ از روی معادلات تعادل در صفحه xy به دست می‌آیند.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

به همین دلیل، این تنش‌ها مستقل از تنش نرمال σ_z هستند. در نتیجه می‌توان از معادلات تعادل تنش صفحه‌ای و دایره مور تنش صفحه‌ای به منظور تعیین مقادیر σ و τ در حالت تنش سه‌محوری نیز استفاده کرد. این موضوع برای محاسبه تنش‌های نرمال و برشی اعمال شده بر روی صفحات مورب و موازی با محورهای x و y نیز صادق است.

تنش‌های برشی ماکسیمم

در مبحث «تنش‌های اصلی و تنش‌های برشی ماکسیمم» دیدیم که اختلاف زاویه بین تنش‌های اصلی و تنش‌های برشی ماکسیمم 45 درجه است.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

به این ترتیب، برای ماده‌ای که تحت تنش سه محوری قرار دارد نیز تنش‌های برشی ماکسیمم در زاویه 45 درجه نسبت به محورهای y ،x و z رخ می‌دهند.

اگر المانی به اندازه 45 درجه نسبت به محور z دَوران یابد، تنش‌های برشی ماکسیمم مثبت و منفی اعمال شده بر روی آن از طریق رابطه زیر محاسبه می‌شوند:

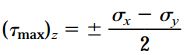
به همین ترتیب، در صورت دوران المان حول محورهای x و y تحت زاویه 45 درجه، تنش‌های برشی ماکسیمم به کمک روابط زیر به دست می‌آیند:

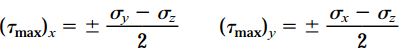
بزرگ‌ترین مقدار به دست آمده از روابط بالا، تنش برشی ماکسیمم مطلق گفته می‌شود. مقدار این تنش با نصفِ اختلافِ بین بزرگ‌ترین و کوچک‌ترین تنش اصلی برابری می‌کند. با استفاده از دایره مور می‌توان رابطه بین تنش‌های اعمال شده بر روی المان‌های دوران یافته تحت زوایای مختلف نسبت به محورهای y ،x و z را به صورت گرافیکی نمایش داد.

شکل زیر، دایره‌های مربوط به المان‌های دوران‌یافته حول محورهای y ،x و z به ترتیب با حروف C ،B و A نشان داده شده‌اند. توجه داشته باشید که رسم دایره A با در نظر گرفتن شرط σ_x>σ_y و همچنین کششی بودن تنش‌های σ_x و σ_y صورت گرفته است.

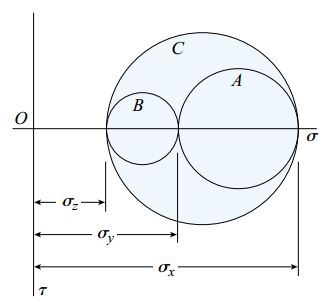
شعاع هر یک از این دایره‌ها با تنش‌های برشی ماکسیمم و شعاع بزرگ‌ترین دایره با تنش برشی ماکسیمم مطلق برابر است. مقادیر تنش‌های نرمال اعمال شده بر روی صفحات دربرگیرنده تنش‌های برشی ماکسیمم نیز با طول مرکز هر دایره بر روی محور افقی دستگاه مختصات برابری می‌کنند.

در این مقاله، وضعیت تنش تنها بر روی صفحات دوران‌یافته حول محورهای y ،x و z مورد تحلیل قرار گرفت. در این حالت، تمام صفحات مورد بررسی با یکی از محورهای مختصات موازی هستند. به عنوان مثال، صفحه مورب نمایش داده شده در شکل زیر با محور z و بردار نرمال آن با صفحه xy موازی است.

امکان در نظر گرفتن صفحاتی که با هیچ‌یک از محورهای مختصات موازی نباشند نیز وجود دارد. در این حالت، مقادیر تنش‌های نرمال و برشی اعمال شده بر روی صفحات مورد بررسی از طریق تحلیل‌های سه‌بعدی پیچیده‌تر به دست می‌آیند. اگرچه، مقادیر تنش‌های نرمال اعمال شده بر روی این صفحات در محدوده‌ای بین تنش‌های اصلی ماکسیمم و مینیمم قرار خواهند گرفت. به علاوه، مقادیر تنش‌های برشی نیز کوچک‌تر از تنش برشی ماکسیمم مطلق خواهند بود.

قانون هوک برای تنش سه محوری

اگر ماده تشکیل‌دهنده المان مورد بررسی از قانون هوک پیروی کند، امکان به دست آوردن رابطه بین تنش‌های نرمال و کرنش‌های نرمال فراهم می‌شود. با جمع کردن مقادیر کرنش‌های حاصل از تنش‌های σ_y ،σ_x و σ_z می‌توان کرنش کل را تعیین کرد.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

به این ترتیب، روابط زیر برای محاسبه کرنش‌های حاصل از تنش‌های سه‌محوری مورد استفاده قرار می‌گیرند:

در روابط بالا از قواعد علامت‌گذاری استاندارد استفاده شده است (علامت مثبت برای تنش کششی σ و کرنش کششی ε). به منظور محاسبه تنش‌ها با توجه به مؤلفه‌های کرنش نیز می‌توان از روابط زیر استفاده کرد:

روابط ارائه شده در این بخش با عنوان قانون هوک برای حالت تنش سه‌محوری شناخته می‌شوند. با جایگذاری مقدار σ_z=0 در روابط بالا، معادلات قانون هوک برای حالت تنش دومحوری به دست می‌آیند.

تغییرات حجم واحد

در حالت تنش سه‌محوری، تغییرات حجم واحد یا «اتساع» (Dilatation) برای المانی که تحت کرنش‌های نرمال ε_y ،ε_x و ε_z قرار دارد، به صورت زیر تعیین می‌شود:

فیلم آموزش مقاومت مصالح ۲ + مفاهیم کلیدی در فرادرس

کلیک کنید

در هنگام رخ دادن کرنش‌های کوچک می‌توان این رابطه را برای تمام مواد مورد استفاده قرار داد. اگر ماده از قانون هوک پیروی کند، با جایگذاری کمیت‌های تنش به جای کرنش به رابطه زیر می‌رسیم:

دو رابطه ارائه شده در این بخش، برای محاسبه اتساع در حالت تنش سه‌محوری با توجه به کمیت‌های کرنش و تنش مورد استفاده قرار می‌گیرد.

چگالی انرژی کرنشی

در صورتی که تنها تنش‌های σ_x و σ_y بر روی یک المان اعمال شوند (حالت تنش دومحوری)، چگالی انرژی کرنشی از رابطه زیر به دست می‌آید:

در صورت سه‌محوری بودن حالت تنش، رابطه چگالی انرژی کرنشی به صورت زیر نوشته می‌شود:

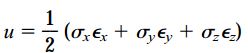
با جایگزین کردن مؤلفه‌های کرنش با تنش (با استفاده از قانون هوک)، رابطه‌ای برای محاسبه چگالی انرژی کرنشی بر حسب مؤلفه‌های تنش به دست می‌آید:

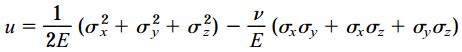
به طور مشابه، با جایگزین کردن مؤلفه‌های تنش با کرنش (با استفاده از قانون هوک)، رابطه‌ای برای محاسبه چگالی انرژی کرنشی بر حسب مؤلفه‌های کرنش به دست می‌آید:

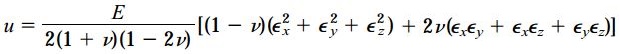
توجه داشته باشید که باید در هنگام جایگزین کردن مؤلفه‌های تنش و کرنش، از علامت مناسب آن‌ها استفاده کرد.

تنش کروی

اگر تمامی تنش‌های نرمال اعمال شده بر روی یک المان با هم برابر باشند، یک حالت خاص از تنش سه‌محوری به نام «تنش کروی» (Spherical Stress) رخ می‌دهد:

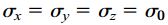
در این حالت، تمامی مقاطع المان در معرض تنش نرمال σ₀ قرار خواهند گرفت. به علاوه، هیچ کرنش برشی بر روی المان اعمال نخواهد شد. با وجود تنش‌های نرمال برابر در تمام جهات و صفر بودن تنش‌های برشی در تمام نقاط، هر صفحه مورد نظر به عنوان یک صفحه اصلی در نظر گرفته می‌شود.

فیلم آموزش الاستیسیته ۱ – حل تمرین در فرادرس

کلیک کنید

به علاوه، دوایر مور نیز به یک نقطه منفرد تبدیل می‌شوند. در حالت تنش کروی، مقادیر کرنش‌های نرمال نیز در تمام جهات یکسان خواهند بود. این موضوع باعث یکنواخت و همسانگرد بودن ماده می‌شود. اگر قانون هوک در این شرایط حکم‌فرما باشد، کرنش‌های نرمال از رابطه به دست می‌آیند:

این رابطه مشابه رابطه تعیین کرنش‌های نرمال در حالت کلی تنش سه‌محوری است. از آنجایی که در حالت تنش کروی هیچ تنش برشی وجود ندارد، اندازه المان تحت تنش تغییر می‌کند اما شکل آن ثابت باقی می‌ماند. به طور کلی، در صورت اعمال تنش کروی به یک جسم، نسبت بین ابعاد آن تغییری نخواهد کرد اما با توجه به کششی یا فشاری بودن تنش، حجم جسم با انبساط یا انقباض مواجه می‌شود. به منظور محاسبه اتساع المان در این حالت می‌توانیم از رابطه زیر استفاده کنیم:

رابطه بالا معمولاً با استفاده از کمیت «مدول حجمی الاستیسیته» (Volume Modulus of Elasticity) یا «مدول بالک» (Bulk Modulus) به صورت جمع و جورتر بیان می‌شود. رابطه زیر، تعریف ریاضی مدول حجمی را نمایش می‌دهد:

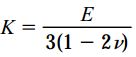
با در نظر داشتن رابطه مدول حجمی (K)، رابطه اتساع یا کرنش حجمی به فرم زیر درمی‌آید:

به این ترتیب، داریم:

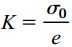
با توجه به رابطه بالا می‌توانیم مدول حجمی را به صورت نسبت تنش کروی به کرنش حجمی تعریف کنیم. این تعریف، معادل تعریف مدول الاستیسیته در حالت تنش تک‌محوری است. توجه داشته باشید که روابط ارائه شده برای تعیین e و K بر اساس فرض کوچک بودن کرنش‌ها و پیروی ماده از قانون هوک به دست آمده‌اند. با توجه به رابطه K بر حسب E و ν، در صورتی که نسبت پواسون برابر با 1/3 باشد، مدول‌های الاستیسیته و حجمی با هم برابر خواهند بود. اگر ν=0 باشد، K برابر با E/3 و اگر ν=0.5 باشد، K برابر با بی‌نهایت خواهد بود. بی‌نهایت بودن مدول حجمی بیانگر صلب بودن ماده و عدم تغییر حجم (غیر قابل تراکم بودن) آن در اثر اعمال تنش است.

روابط ارائه شده برای حالت تنش کروی با در نظر گرفتن شرایط کشش یکنواخت در تمام جهات به دست آمدند. این روابط برای شرایط تراکم یکنواخت نیز قابل استفاده هستند. توجه داشته باشید که در این حالت، علامت تنش‌ها و کرنش‌ها منفی خواهد بود. تراکم یکنواخت زمانی رخ می‌دهد که ماده در تمام جهات تحت فشار یکنواخت قرار گرفته باشد. اجسام زیر آب یا سنگ‌های درون اعماق زمین را می‌توان به عنوان مصادیق مواد تحت فشار یکنواخت در نظر گرفت. این حالت تنش اغلب با عنوان «تنش هیدرواستاتیک» (Hydrostatic Stress) شناخته می‌شود.

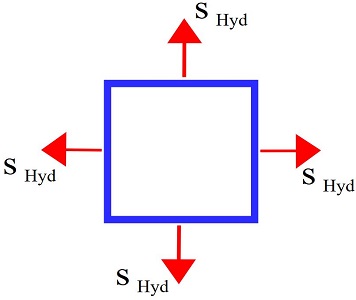
فشار یکنواخت به عنوان یک حالت رایج در مسائل مختلف محسوب می‌شود اما دستیابی به حالت کشش یکنواخت یک امر دشوار به شمار می‌رود. با افزایش ناگهانی و یکنواخت دمای سطح خارجی یک گوی فلزی می‌توان حالت کشش یکنواخت را به وجود آورد. در این فرآیند، دمای لایه‌های خارجی بیشتر از لایه‌های داخلی خواهد بود. به این ترتیب، تمایل لایه‌های خارجی به انبساط، باعث به وجود آمدن کشش یکنواخت نقطه مرکز گوی در راستای تمام جهات خواهد شد.

^^