پایداری روش تفاضل محدود – به زبان ساده

در مطالب قبلی وبلاگ فرادرس، علم دینامیک سیالات محاسباتی به صورت کامل مورد بررسی قرار گرفت. همانطور که نشان داده شد، به جای انجام آزمایش‌های تجربی در تونل باد، می‌توان با حل عددی معادلات به کمک روش‌های مختلف مانند روش تفاضل محدود، حجم محدود و المان محدود، ویژگی‌های مختلف میدان جریان سیال اطراف یا درون اجسام (مانند سرعت، دما و فشار) را محاسبه کرد. انتخاب این روش‌های عددی به هندسه موجود و ویژگی‌های سیال بستگی دارد. علاوه بر موارد ذکر شده، مطالعه پایداری روش‌های عددی مانند بررسی پایداری روش تفاضل محدود نیز نقش اساسی را در انتخاب این روش‌ها و اجرای یک حل عددی صحیح ایفا می‌کند.

این مطلب ابتدا به صورت دقیق به معرفی عدد کورانت یا عدد CFL می‌پردازد و شرط پایداری را با استفاده از این عدد برای برخی از حالات موجود در روش تفاضل محدود مورد مطالعه قرار می‌دهد. در ادامه با استفاده از ماتریس پایداری، روش‌های مختلف تفاضل محدود از نظر پایداری ارزیابی می‌شوند. در انتها نیز دو مثال و یک کد متلب برای درک بهتر روش تفاضل محدود و پایداری آن بیان می‌شود.

شرایط CFL

همانطور که اشاره شد بررسی پایداری روش‌های مختلف عددی، یکی از مباحث بسیار مهم است که کاربرد زیادی در علوم توربوماشین و آیرودینامیک دارد و پایداری حل‌های عددی انجام شده در این علوم اهمیت بسیار زیادی دارد. بنابراین هدف اصلی این مطلب بررسی پایداری روش تفاضل محدود است. بر این اساس در قدم اول، شرایط Courant-Friedrichs-Levy را به منظور بررسی پایداری روش‌های تفاضل محدود برای معادلات هذلولوی مورد مطالعه قرار می‌دهیم. توجه کنید که این شرایط یعنی Courant-Friedrichs-Levy را با نماد اختصاری CFL نیز نمایش می‌دهند.

در برخی از مسائل دینامیک سیالات محاسباتی که در آن‌ها با استفاده از روش تفاضل محدود به صورت عددی معادلات ناویر استوکس و پیوستگی حل می‌شوند، محدودیت‌هایی وجود دارد. یکی از محدودیت‌ها بحث پایداری این روش‌ها است. برای مثال، زمانی که گام زمانی افزایش می‌یابد و اندازه شبکه ثابت است، روش FTBS در نهایت ناپایدار می‌شود.

روش FTBS، گسسته سازی معادلات را به صورت پیشرو و گسسته سازی در مکان را به صورت پسرو انجام می‌دهد. برای آشنایی بیشتر و دقیق‌تر با شیوه گسسته سازی معادلات و آشنایی با روش FTBS به مطلب «روش تفاضل محدود (Finite Difference Method) — از صفر تا صد» مراجعه کنید.

البته حالت دیگری نیز برای ناپایدار شدن حل وجود دارد. در این حالت با کاهش سایز شبکه و ثابت ماندن گام زمانی، روش FTBS در نهایت ناپایدار می‌شود. بنابراین واضح است که انتخاب گام زمانی مستقل از سایز شبکه نیست و بنابراین به منظور حفظ پایداری حل، اندازه گام زمانی و سایز شبکه باید با یکدیگر به صورت هماهنگ تغییر کنند.

نکته دیگری که باید به آن اشاره کرد این است که در یک حل عددی می‌توان ناحیه‌ای را تعیین کرد که حل در یک نقطه مانند $$(x_ i , t ^ n )$$ به مقادیر موجود در آن ناحیه بستگی دارد. شکل زیر «ناحیه وابستگی حل عددی» (Numerical Domain of Dependence) در روش FTBS نشان می‌دهد.

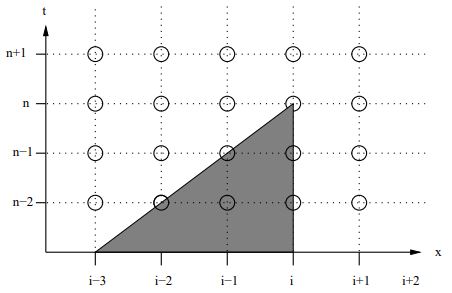
این ناحیه وابستگی حل عددی را با استفاده از خطوط مشخصه در انواع معادلات با مشتقات جزئی نیز می‌توان به خوبی مورد مطالعه قرار داد.

یکی از شرط‌های اساسی برای همگرایی یک روش تفاضل محدود که برای معادله دیفرانسیل با مشتقات جزئی (PDE) هذلولوی نوشته شده، این است که ناحیه وابستگی حل عددی شامل «ناحیه وابستگی ریاضی» (Mathematical Domain of Dependence) باشد. این موضوع را با استفاده از شرط Courant-Friedrichs-Levy یا شرط کوارنت مورد بررسی قرار می‌دهند. این شرط را به صورت اختصاری با نماد CFL نیز نمایش می‌دهند. این شرط به افتخار نویسنده آن که برای اولین بار این شرایط را مورد بررسی قرار داد، به این نام شناخته می‌شود.

به عنوان مثال، برای معادله یک بعدی جابه‌جایی که با استفاده از «الگوریتم بادسو» (Upwind Scheme) یا آپویند گسسته شده، شرط کورانت یا CFL رابطه زیر را برای پایداری حل الزامی می‌داند.

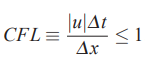
عددی که در بالا نشان داده شده است یعنی $${|x| \Delta t} \over {\Delta x}$$ را عدد کورانت یا عدد CFL می‌نامند. همچنین همانطور که اشاره شد، این عدد را به صورت خلاصه با نماد CFL نیز نمایش می‌دهند.

به صورت کلی می‌توان بیان کرد که شرط پایداری برای روش‌های تفاضل محدود «صریح» (Explicit) این است که عدد کورانت یا عدد CFL با استفاده از یک عدد ثابت محدود شده باشد. این عدد ثابت به روش عددی خاصی که استفاده شده، وابستگی شدیدی دارد.

ماتریس پایداری برای روش‌های تفاضل محدود

در مطلب روش تفاضل محدود، نشان داده شد که یک تقریب تفاضل محدود را می‌توان به شکل یک معادله نیمه گسسته نوشت. فرم نهایی این معادله به شکل زیر قابل نمایش است.

تعداد بسیار زیادی از روش‌های گسسته‌سازی معادلات دیفرانسیل با مشتقات جزئی حضور دارند که می‌توان آن‌ها را به فرم معادله بالا بیان کرد و تعداد زیادی از این روش‌ها نیز موجود هستند که در نهایت به فرم بالا در نمی‌آیند. در این بخش و در ادامه، معادله نیمه گسسته بالا را به عنوان نقطه شروع خود در نظر می‌گیریم.

فیلم آموزش دینامیک سیالات محاسباتی CFD 1 در فرادرس

کلیک کنید

فرض کنید که (U(t پاسخ دقیق ریاضی معادله نیمه گسسته فوق باشد. در این حالت، آشفتگی و اختلالی را به فرم (e(t برای این معادله در نظر بگیرید که با پاسخ دقیق ((U(t) جمع می‌شود. با استفاده از این فرضیات، فرم نهایی پاسخ به شکل زیر در می‌آید.

در ادامه به دنبال یافتن پاسخ برای دو سوال اساسی در روش تفاضل محدود هستیم. سوال اول این است که آشفتگی و اختلال (e(t برای یک مسئله نیمه گسسته، در طول زمان رشد می‌کند؟ سوال بعدی این است که برای ارضای پایداری یک روش انتگرالی زمانی چه محدودیت‌هایی وجود دارد و گام زمانی چگونه باید انتخاب شود؟

بنابراین در گام اول و به منظور یافتن پاسخی مناسب برای سوال‌های بالا، (V(t را در رابطه ۲ قرار می‌دهیم. بنابراین رابطه ۲ به شکل زیر در می‌آید.

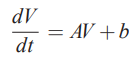
حال از رابطه ۳ برای نوشتن (V(t استفاده می‌کنیم و مقادیر موجود در این رابطه را در معادله فوق (رابطه 4) جایگذاری می‌کنیم.

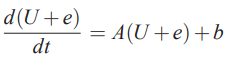
با مقایسه معادله فوق (رابطه ۵) با معادله ابتدای این بخش (رابطه ۲)، ساده سازی‌ها را انجام می‌دهیم و در نهایت رابطه زیر به دست می‌آید.

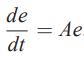
بنابراین اغتشاش و اختلال موجود در جریان باید معادله همگن بالا را ارضا کند. مطالعه معادلات خطی مانند معادله بالا، نشان می‌دهد که مقدار (e(t با افزایش زمان بدون محدودیت افزایش می‌یابد. البته توجه کنید که شرط این موضوع این است که تمام قسمت‌های حقیقی «مقادیر ویژه» (Eigenvalue) ماتریس A، مثبت باشند.

یکی از مسائل اساسی که در روند بالا حضور دارد، این است که یافتن مقادیر ویژه A کار راحت و بدیهی نیست. در واقع برای یک مسئله در حالت عمومی، یافتن مقادیر ویژه A به اندازه حل یک مسئله از صفر تا صد، می‌تواند چالش برانگیز و پیچیده باشد. بنابراین از آنجایی که روش ماتریس پایداری، یک روش عمومی است، برای عملکرد آن نیاز به صرف زمان زیادی داریم. با این وجود، هنوز روش پایداری ماتریسی به عنوانی یکی از بخش‌های ضروری در تحلیل‌های عددی به حساب می‌آید.

همانطور که در تحلیل مقدار ویژه مربوط به روش انتگرالی «معادلات دیفرانسیل معمولی» (Ordinary Differential Equation) مشاهده شد، روش انتگرالی باید برای تمام مقادیر ویژه موجود در مسئله، پایدار باشد. یکی از روش‌هایی که با استفاده از آن می‌توانیم پایداری را مورد مطالعه قرار دهیم، این است که مقادیر ویژه مقیاس شده به وسیله گام زمانی را در صفحه مختلط λ Δt رسم کنیم و در نهایت با ناحیه مطلوب برای پایداری انتگرال معادله دیفرانسیل معمولی مقایسه کنیم. در این شرایط مقدار گام زمانی برای پایدار شدن تمام مقادیر ویژه انتگرال معادله دیفرانسیل معمولی مشخص می‌شوند.

روندی که در بالا به صورت دقیق و با جزئیات توضیح داده شد را در مثال زیر به کار می‌بریم و شما با استفاده از مثال زیر، به صورت کامل با شیوه بررسی پایداری روش تفاضل محدود، آشنا خواهید شد.

مثال 1

در این مثال به بررسی ماتریس پایداری روش FTCS برای «جابه‌جایی یک بعدی» ($$1-D \enspace Convection$$) پرداخته می‌شود.

به صورت مختصر می‌توان بیان کرد که روش FTCS خلاصه شده عبارت Forward Time, Central Space است که با اعمال آن، مشتق زمانی به صورت پیش‌رو و مشتق مکانی به صورت مرکزی در سیستم معادلات اعمال می‌شود.

روش FTCS در مطلب «روش تفاضل محدود (Finite Difference Method) — از صفر تا صد» به صورت کامل مورد مطالعه قرار گرفته است و شیوه نمایش آن برای معادله جابه‌جایی یک بعدی نیز بررسی شد. بنابراین با اعمال روش FTCS به معادله جابه‌جایی یک بعدی، فرم نهایی معادله به شکل زیر در می‌آید.

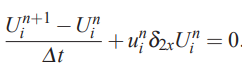
یکی از نکات بسیار مهمی که باید به آن اشاره کرد این است که رابطه بالا به شکل صریح نوشته شده و نیاز به تشکیل مستقیم ماتریس A نیست.

همانطور که مشاهده می‌شود با استفاده از معادله 7، اطلاعات جدید برای هر U مربوط به نقطه i قابل محاسبه است. این موضوع با استفاده از کد متلب مربوط به آن به خوبی نشان داده شده است. در این شرایط، تنها در شرایطی نیاز به محاسبه ماتریس A است که بررسی پایداری و محاسبه مقادیر ویژه موضوع مهمی برای ما باشد. در ادامه دقیقا همین عمل انجام خواهد شد.

به عبارت دیگر، روندی که در ادامه طی می‌شود به ترتیب این است که در ابتدا ماتریس A و مقادیر ویژه ماتریس A محاسبه می‌شوند و در ادامه مقادیر ویژه مقیاس شده با استفاده از گام زمانی (Δt)، توسط ناحیه پایداری اویلر پیشرو پوشش داده می‌شود.

توجه کنید که این کد می‌تواند شرایط مرزی مانند «پریودیک» (Periodic) و «جریان ورودی» (Inflow) - «جریان خروجی» (Outflow) را مورد مطالعه قرار دهد. این شرایط در مثال موجود در مطلب «روش تفاضل محدود» بررسی شد. بنابراین در ادامه به بررسی پایداری و مقادیر ویژه در هر دو حالت شرایط مرزی پرداخته می‌شود.

1 % This Matlab script solves the one-dimensional convection
2 % equation using a finite difference algorithm. The
3 % discretization uses central differences in space and forward
4 % Euler in time.
5 %
6 % periodic bcs are set if periodic flag == 1
7 %
8
9 clear all;
10 close all;
11
12 periodic_flag = 1;
13
14 % Number of points
15 Nx = 20;
16 x = linspace(0,1,Nx+1);
17 dx = 1/Nx;
18
19 % velocity
20 u = 1;
21
22 % Set timestep
23 CFL = 1;
24 dt = CFL*dx/abs(u);
25
26 % Allocate matrix to hold stiffness matrix (A).
27 A = zeros(Nx,Nx);
28
29 % Construct A except for first and last row
30 for i = 2:Nx-1,
31 A(i,i-1) = u/(2*dx);
32 A(i,i+1) = -u/(2*dx);
33 end
34
35 if (periodic_flag == 1), % Periodic bcs
36
37 A(1 ,2 ) = -u/(2*dx);
38 A(1 ,Nx ) = u/(2*dx);
39 A(Nx,1 ) = -u/(2*dx);
40 A(Nx,Nx-1) = u/(2*dx);
41
42else % non-periodic bc's
43
44 % At the first interior node, the i-1 value is known (UL).
45 % So, only the i+1 location needs to be set in A.
46 A(1,2) = -u/(2*dx);
47
48 % Outflow boundary uses backward difference
49 A(Nx,Nx-1) = u/dx;
50 A(Nx,Nx ) = -u/dx;
51 end
52
53 % Calculate eigenvalues of A
54 lambda = eig(A);
55
56 % Plot lambda*dt
57 plot(lambda*dt,'*');
58
59 xlabel('Real \lambda\Delta t');
60 ylabel('Imag \lambda\Delta t');
61
62 % Overlay Forward Euler stability region
63 th = linspace(0,2*pi,101);
64 hold on;
65 plot(-1 + sin(th),cos(th));
66 hold off;
67 axis('equal');
68 grid on;

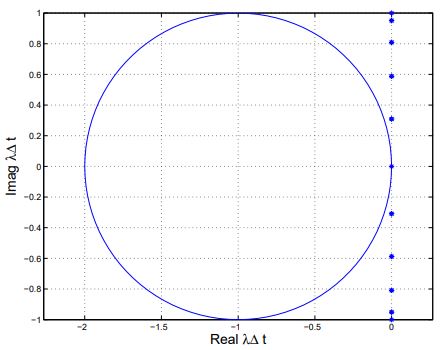
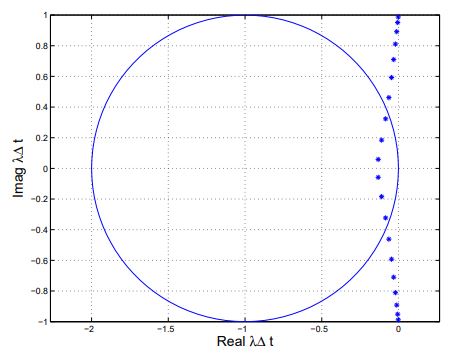
در ادامه منحنی λ Δt برای حالتی رسم می‌شود که در آن مقدار CFL برابر با یک قرار داده شده است. این موضوع در شکل‌های ادامه این مطلب به خوبی نمایش داده شده است. توجه کنید که برای یک مسئله یک بعدی عدد CFL به شکل زیر تعریف می‌شود.

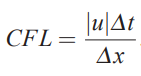
همانطور که در شکل‌های بالا مشاهده می‌شود، شرط مرزی پریودیک، مقادیر ویژه موهومی تولید می‌کند که این مقادیر با فاصله گرفتن از مرکز به سمت $$\pm i$$ حرکت می‌کند. توجه کنید که در حقیقت شرط مرزی پریودیک مقدار ویژه برابر با صفر تولید می‌کند، بنابراین ماتریس A منفرد و تکین است.

نکته دیگر این است که در شرایط مرزی ورودی و خروجی، مقادیر ویژه درون ناحیه با قسمت حقیقی منفی حرکت می‌کند. اما در این حالت نیز با فاصله گرفتن از مرکز، به مقادیر موهومی $$\pm i$$ میل می‌کند.

توجه کنید که برخی از مقادیر λ Δt وجود دارند که در خارج از ناحیه پایداری اویلر قرار گرفته‌اند. در نتیجه ما می‌توانیم با استفاده از کاهش مقدار گام زمانی تمام مقادیر λ Δt را به درون ناحیه پایداری منتقل کنیم. اما اثبات می‌شود که این کار به صورت عملی غیر ممکن است؛ زیرا در نهایت مقادیر ویژه به سمت $$\pm i$$ میل می‌کنند. بنابراین می‌توان نتیجه گرفت که هیچ مقدار محدودی برای گام زمانی Δt وجود ندارد که به کمک آن بتوان مقادیر ویژه را به داخل ناحیه پایداری دایروی مربوط به روش اویلر پیشرو منتقل کرد.

توضیحات بالا نشان می‌دهد که روش FTCS برای جابه‌جایی ناپایدار است.

نکته مهم دیگری که در ادامه به صورت دقیق مورد مطالعه قرار می‌گیرد، بررسی شیوه تغییرات طیف مقادیر ویژه ماتریس A با تغییر اندازه شبکه Δx است.

فیلم آموزش شبیه سازی مسائل جریان سیال و انتقال حرارت با فرترن Fortran + گواهینامه در فرادرس

کلیک کنید

در بخش قبل مشاهده شد که برای معادله «جابه‌جایی» (Convection) با تغییر و اصلاح مقدار Δx باید مقدار Δt نیز اصلاح شود تا عدد CFL ثابت باقی بماند و پایداری حفظ شود. بنابراین تحت شرایط بیان شده و برای یک CFL ثابت، انتظار داریم که طیف مقدار ویژه با تغییر تعداد نقاط تغییر خاصی نکند.

شکل‌های زیر مقادیر ویژه هنگام حضور شرایط مرزی پریودیک و دریکله را در حالتی رسم کرده که پارامتر Δx با ضریب 10 اصلاح شده و به عبارت دیگر تعداد نقاط شبکه حل ۱۰ برابر شده است.

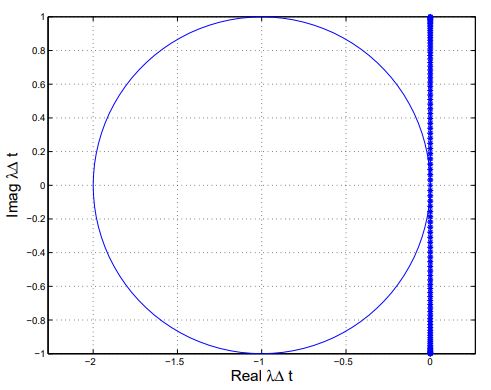
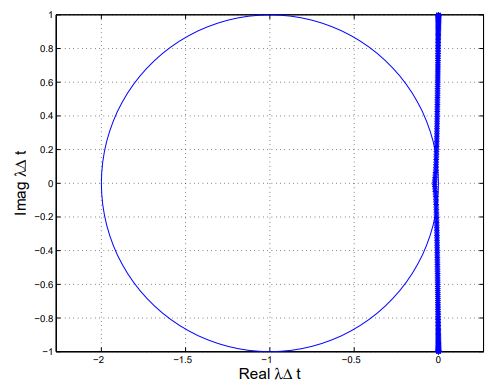
همانطور که مشاهده می‌شود، در حالتی که شرایط مرزی به صورت پریودیک است، ما همچنان مقادیر ویژه موهومی که به $$\pm i$$ میل می‌کند را مشاهده می‌کنیم و زمانی که شرایط مرزی دریکله داریم، همچنان مقادیر به صورت اندک در ناحیه منفی قرار می‌گیرند ولی نسبت به مش درشت تر یعنی شکل 3 مقادیر به سمت محور موهومی نزدیک‌تر شده‌اند.

توجه کنید که در شکل‌های بالا نیز Δt طوری در نظر گرفته شده است که همانند حالت قبل، پارامتر CFL برابر با یک باشد.

نکته بسیار مهم دیگری که از توضیحات و شکل‌های بالا می‌توان دریافت این است که مقادیر ویژه مربوط به شرط مرزی دریکله با ریز شدن هندسه به سمت نتایج حاصل از شرط مرزی پریودیک حرکت می‌کند. بنابراین ما می‌توانیم از مزایای این ویژگی استفاده کنیم و پایداری روش تفاضل محدود خود را بررسی کنیم بدون آنکه شرایط مرزی دقیق را در نظر گرفته باشیم.

محاسبه مقادیر ویژه ماتریس A، در حالت عادی معمولا نیاز به استفاده از روش‌های عددی مختلفی دارد. یکی از حالات خاص، حالتی است که ماتریس به صورت پریودیک باشد. در واقع حالت پریودیک ماتریس به شکل زیر تعریف می‌شود.

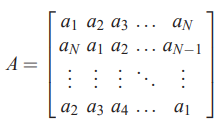
برای آنکه به صورت دقیق ویژگی‌های ماتریس بالا را متوجه شوید، کافی است که به ستون‌های آن، عناصر موجود در قطر اصلی، شروع و پایان هریک از ستون‌ها دقت کنید. این نوع از ماتریس را «ماتریس دوری یا گردشی» (Circulant Matrix) نیز می‌نامند و مقادیر ویژه آن با استفاده از رابطه زیر قابل محاسبه هستند.

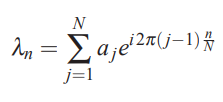
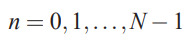
مثال 2

همانطور که در مثال قبل مشاهده شد، زمانی که شرط مرزی پریودیک اعمال می‌شود، گسسته سازی مرکزی معادله مربوط به پدیده یک بعدی جابه‌جایی، نتایجی را به صورت موهومی ارائه می‌کند و زمانی که مقادیر ویژه با استفاده از گام زمانی برای حالتی که CFL برابر با یک است، مقیاس می‌شود، مقادیر ویژه در طول محور بین مقادیر $$\pm i$$ دیده می شوند. این موضوع در شکل‌های بالا به صورت دقیق نشان داده شده است.

توجه کنید که برای یک مسئله «جابه‌جایی» (Convection) که سرعت در آن مقداری ثابت دارد و شرط مرزی پریودیک اعمال شده است، ماتریس به صورت دوری یا گردشی خواهد بود. بنابراین ما می‌توانیم از معادله 10 استفاده کنیم و مقادیر ویژه را به صورت تحلیلی محاسبه کنیم. بنابراین در ابتدا ضرایب a_j را محاسبه می‌کنیم.

برای گسسته سازی مرکزی داریم:

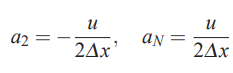
توجه کنید که مقادیر ضرایب a_j برای سایر jها برابر با صفر است. با قرار دادن مقادیر ضرایب a_j در معادله ۱۰، مقادیر ویژه به فرم زیر محاسبه می‌شوند.

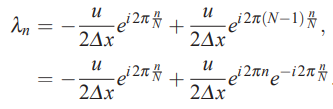
برای ساده سازی معادله بالا از این نکته استفاده می‌شود که رابطه $$e^{i 2 \pi n} = 1$$ برقرار است. بنابراین رابطه فوق به شکل زیر در می‌آید.

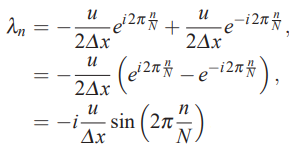
در صورتی که عبارت فوق را در گام زمانی ضرب کنیم، در نهایت معادله به شکل زیر در می‌آید.

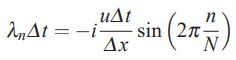
بنابراین همانطور که در مثال 1 نیز به صورت دقیق مورد بررسی قرار گرفت، مقادیر ویژه مربوط به حل یک بعدی جابه‌جایی به صورت موهومی هستند. این موضوع در اینجا نیز نشان داده شد. بنابراین در  شرایط خاص این مسئله نیز زمانی که شرط مرزی به صورت پریودیک است، مقادیر ویژه به صورت موهومی هستند. نکته دیگری که باید به آن اشاره کرد این است که وقتی مقدار CFL برابر با یک است ($$CFL = |u| \Delta t / \Delta x = 1$$)، مقادیر ویژه در محدوده $$\pm i$$ قرار می‌گیرند.

بنابراین همانطور که اشاره شد، بررسی پایداری روش‌های مختلف عددی در علم دینامیک سیالات محاسباتی مانند روش تفاضل محدود با استفاده از روش‌های گوناگون انجام می‌شود که این روش‌ها نیاز به انجام محاسبات دقیق دارند. همچنین گام زمانی و اندازه شبکه مناسب موجود در حل باید طوری تعیین شوند که شرط پایداری را ارضا کنند. انتخاب نامناسب این دو پارامتر، می‌تواند حل عددی ما را ناپایدار کند و در نهایت حل عددی واگرا شود.

این مطلب ابتدا به صورت دقیق به معرفی عدد کورانت یا عدد CFL پرداخت و شرط پایداری را با استفاده از این عدد برای برخی از حالات موجود در روش تفاضل محدود مورد مطالعه قرار داد. در ادامه با استفاده از ماتریس پایداری، روش‌های مختلف تفاضل محدود از نظر پایداری ارزیابی شدند و در انتها نیز دو مثال و یک کد متلب برای درک بهتر روش تفاضل محدود و پایداری آن بیان شدند.

^^