فرادرسکواترنیون یا چهارگان چیست؟ – به زبان ساده
در علم ریاضیات، کواترنیون ها یا چهارگانها (Quaternions) یک دستگاه عددنویسی برای بسط اعداد مختلط هستند. آنها اولین بار توسط ریاضی‌دان ایرلندی، ویلیام همیلتون، در سال 1843 معرفی و در حوزه مکانیک در فضای سه بعدی به کار گرفته شدند. یکی از ویژگی‌های کواترنیون‌ها این است که ضرب دو کواترنیون خاصیت جابه‌جایی ندارد. همیلتون، یک کواترنیون را به صورت خارج قسمت دو خط جهت‌دار در یک فضای سه بعدی، و یا معادل آن، یعنی خارج قسمت دو بردار تعریف کرده است.
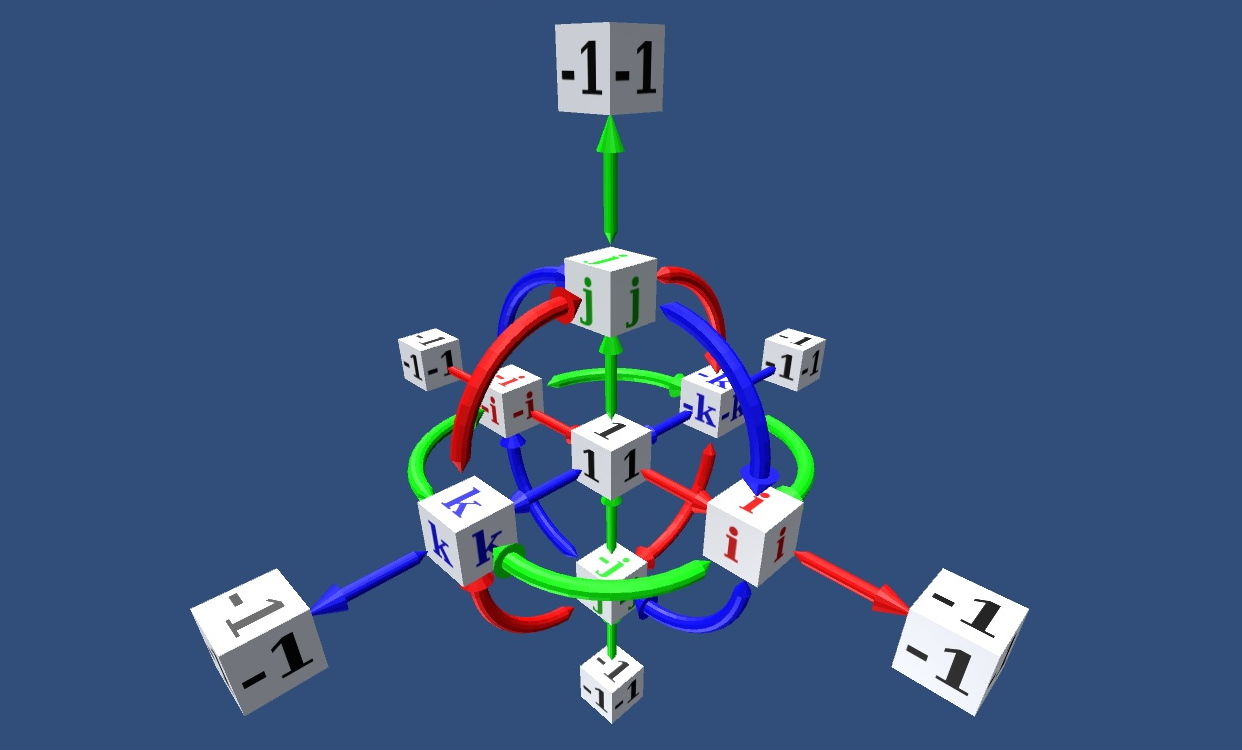
کواترنیون‌ها هم در ریاضیات نظری و هم کاربردی، به خصوص برای محاسباتی که شامل چرخش سه بعدی هستند همچون گرافیک کامپیوتری سه بعدی، بینایی کامپیوتر و تحلیل بافت کریستالوگرافی، به کار می‌روند. در کاربردهای عملی، از کواترنیون‌ها می‌توان در کنار سایر روش‌ها همچون زاویه اویلر و ماتریس دوران استفاده کرد و یا گاهی به جای آنها به کار برد.
کواترنیون‌ها اولین جبر ناجابه‌جایی تقسیمی کشف شده هستند. جبر کواترنیون‌ها اغلب توسط $$\mathbf{H}$$ (حرف شروع همیلتون در انگلیسی) نشان داده می‌شود. جبر $$\mathbf{H}$$ اهمیت خاصی در بحث تحلیل دارد، زیرا با توجه به قضیه فروبنیوس (Frobenius)، این جبر یکی از تنها دو مجموعه حلقه تقسیم با ابعاد متناهی شامل اعداد حقیقی به عنوان یک زیرحلقه مناسب است. مجموعه دیگر، اعداد مختلط هستند.
کواترنیون چیست؟
مجموعه کواترنیون‌های $$ \mathbf { H } $$ معادل با $$\mathbb{R}^ 4 $$، یعنی یک فضای برداری چهار بعدی بر روی اعداد حقیقی هستند. $$\mathbf{H}$$ سه عمل جمع، ضرب اسکالر و ضرب کواترنیون دارد. جمع دو عنصر $$ \mathbf{H}$$ به شکل جمع آنها به صورت عناصر $$\mathbb{R}^ 4 $$ تعریف شده است. به طور مشابه، حاصلضرب یک عنصر $$\mathbf{H}$$ در یک عدد حقیقی مانند حاصلضرب در یک اسکالر در $$\mathbb{R}^ 4 $$ تعریف می‌شود. تعریف حاصلضرب دو عنصر در $$\mathbf{H}$$ نیازمند انتخاب پایه برای $$\mathbb{R}^ 4 $$ است. عناصر این پایه با $$1$$، $$i$$، $$j$$ و $$k$$ نشان داده می‌شوند.
هر عنصر $$ \mathbf{H}$$ را می‌توان به صورت یکتا به شکل یک ترکیب خطی از این عناصر پایه نوشت؛ یعنی به صورت $$a1 + bi + cj + dk$$، که در آن، $$a$$، $$b$$، $$c$$ و $$d$$ اعداد حقیقی هستند. عنصر پایه $$1$$، عنصر همانی $$\mathbf{H}$$ است و از آنجایی که ضرب در $$1$$ هیچ تغییری به وجود نمی‌آورد، عناصر $$ \mathbf{H}$$ اغلب با چشم‌پوشی از $$1$$ به صورت $$a + bi + cj + dk $$ نوشته می‌شوند. با این پایه مفروض، تعریف حاصضرب کواترنیون شرکت‌پذیر ابتدا با تعریف حاصلضرب عناصر پایه و سپس با تعریف تمام حاصلضربهای دیگر با استفاده از قانون توزیعی انجام می‌شود.
ضرب عناصر پایه
قرارداد $$ i ^ 2 = j ^ 2 =k^ 2 = ijk = -1 $$ تمام حاصلضربهای ممکن $$i$$، $$j$$ و $$k$$ را تعیین می‌کند که در آن، $$i$$، $$j$$ و $$k$$ عناصر پایه $$\mathbf{H}$$ هستند،. برای مثال با ضرب از راست $$k$$ در هر دو طرف معادله $$ijk=-1$$ داریم:
$$ \large \begin{align*}
- k & = ijkk = ij ( k ^ 2) = ij ( - 1 ), \\
k & = ij .
\end{align*} $$
تمام حاصلضربهای دیگر ممکن را نیز می‌توان با روش‌های مشابهی تعیین کرد که منجر به نتایج زیر می‌شوند:
$$ \large
\begin {alignat} {2}
i j & = k , & \qquad ji & = -k, \\
jk & = i, & kj & = -i, \\
ki & = j, & ik & = -j.
\end{alignat} $$
نتایج مذکور را می‌توانن به صورت جدولی که سطرهایش نماینده عامل سمت چپ حاصلضرب، و ستون‌هایش نماینده عامل سمت راست هستند، نشان داد:
برخلاف ضرب اعداد مختلط یا حقیقی، ضرب کواترنیون‌ها خاصیت جابه‌جایی ندارد. برای مثال $$ij=k$$ است، در حالی که $$ji=-k$$ خواهد بود.
کاربرد کواترنیون در نمایش دوران
کواترنیون تعمیمی از اعداد مختلط با سه عدد موهومی $$ i $$، $$j$$ و $$k$$ است. بنابراین می‌توان گفت کواترنیون یک عدد مختلط با چهار بعد است که می‌توان از آن برای نمایش چرخش یک جسم صلب یا محورها در فضای سه بعدی استفاده کرد. همان‌طور که گفتیم، تعریف عمومی یک کواترنیون به صورت زیر است:
$$ Q=a+b.i+c.j+d.k = \left[
\begin{matrix}
a && b && c && d
\end{matrix}
\right] $$
نمایش دوران
کواترنیون‌ها یک تبدیل چرخشی را در فضای سه بعدی نمایش می‌دهند. ساده‌ترین راه برای نمایش یک کواترنیون تصور چرخش یک زاویه مشخص حول یک بردار معین اس. شکل زیر دوران زاویه $$ \theta $$ را حول بردار $$ \overrightarrow{V}$$ را نشان می‌دهد که با سه اسکالر $$V_x$$، $$V_y$$ و $$ V _ z $$ بیان شده است.
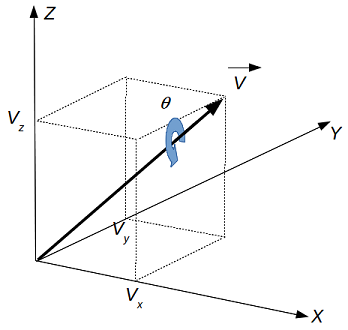
کواترنیون متناظر با این تبدیل به صورت زیر است:
$$ Q =
\left[
\begin{matrix}
q_w &&
q_x &&
q_y &&
q_z
\end{matrix}
\right] $$
$$ Q =
\left[
\begin{matrix}
cos \frac{\theta}{2} &&
V_x.sin \frac{\theta}{2} &&
V_y.sin \frac{\theta}{2} &&
V_z.sin \frac{\theta}{2}
\end{matrix}
\right] $$
چرخش حول محورها
با کمک فرمول بالا، می‌توانیم کواترنیون تعریف کننده چرخش حول هر محور را به صورت زیر محاسبه کنیم:
- چرخش حول محور $$ x $$:
$$ Q_X=\left[
\begin{matrix}
cos \frac{\theta}{2} &&
sin \frac{\theta}{2} &&
0 &&
0
\end{matrix}
\right] $$
- چرخش حول محور $$y$$:
$$ Q_Y=\left[
\begin{matrix}
cos \frac{\theta}{2} &&
0 &&
sin \frac{\theta}{2} &&
0
\end{matrix}
\right] $$
- چرخش حول محور $$ z $$:
$$ Q_Z=\left[
\begin{matrix}
cos \frac{\theta}{2} &&
0 &&
0 &&
sin \frac{\theta}{2}
\end{matrix}
\right] $$
چرخش کلی
اکنون می‌خواهیم مختصات بردار داده شده $$ \overrightarrow{v _A}$$ را با کمک کواترنیون $$ {}^BQ_A $$ محاسبه کنیم. بردار منتجه $$ \overrightarrow{v _B}$$ را می‌توان با فرمول زیر و بر اساس ضرب کواترنیون و مزدوج کواترنیون محاسبه کرد (این دو مورد را در ادامه توضیح می‌دهیم):
$$ \large \overrightarrow{V}_B = {}^BQ_A \otimes \overrightarrow{V}_A \otimes \overline {{}^BQ_A} $$
لازم به ذکر است که $$ \overrightarrow{V _A}$$ و $$ \overrightarrow{V _B}$$ در فضای $$ \mathbb{R}^4$$ و $$ \overrightarrow{v _A}$$ و $$ \overrightarrow{v _B}$$ در فضای $$ \mathbb{R}^ 3$$ هستند. همچنین، $$ \overrightarrow{V _A}$$ و $$ \overrightarrow{V _B}$$ کواترنیون‌های خالصی هستند که بخش‌های حقیقی آنها برابر با صفر است.
$$ \overrightarrow{V}_A = \begin{bmatrix} 0 \\ \overrightarrow{v}_A \end{bmatrix}
= \begin{bmatrix} 0 \\ x_A \\ y_A \\ z_A \end{bmatrix} $$
$$ \overrightarrow{V}_B = \begin{bmatrix} 0 \\ \overrightarrow{v}_B \end{bmatrix}
= \begin{bmatrix} 0 \\ x_B \\ y_B \\ z_B \end{bmatrix} $$
کواترنیون $$ {}^BQ_A $$ تبدیل از قاب $$A$$ به $$ B $$ را نشان می‌دهد.
ضرب کواترنیون:
ضرب کواترنیون با نماد $$ \otimes $$ نشان داده می‌شود و برای دو کواترنیون $$ Q _1$$ و $$ Q _ 2 $$ به صورت زیر است:
$$ Q_1 = \left[ \begin{matrix} a_1 && b_1 && c_1 && d_1 \end{matrix} \right] $$
$$ Q_2 = \left[ \begin{matrix} a_2 && b_2 && c_2 && d_2 \end{matrix} \right] $$
$$ Q_1 \otimes Q_2 =
\left[
\begin{matrix}
a_1a_2 - b_1b_2 - c_1c_2 - d_1d_2 \\
a_1b_2 + b_1a_2 + c_1d_2 - d_1c_2 \\
a_1c_2 - b_1d_2 + c_1a_2 + d_1b_2 \\
a_1d_2 + b_1c_2 - c_1b_2 + d_1a_2
\end{matrix}
\right]^\top $$
ضرب کواترنیون جابه‌جایی پذیر نیست:
$$ Q_1 \otimes Q_2 \neq Q_2 \otimes Q_1 $$
مزدوج کوانتیون:
مزدوج کوانتیون با نمادهای $$ Q^* $$، $$ \overline Q $$ و $$ Q^T $$ نشان داده می‌شود که استفاده از $$ \overline Q $$ رایج‌تر است. مزدوج کواترنیون $$Q$$، به صورت زیر بیان می‌شود:
$$ Q = \left[ \begin{matrix} a && b && c && d \end{matrix} \right] $$
$$ \overline Q = \left[ \begin{matrix} a && -b && -c && -d \end{matrix} \right] $$
دوره آموزش ویدیویی ریشه‌یابی و ترسیم اعداد مختلط در متلب
برای آشنایی بیشتر با کواترنیون و کاربرد آن در اعداد مختلط می‌توانید به دروه آموزش رایگان ویدئویی «ریشه‌یابی و ترسیم اعداد مختلط در متلب» مراجعه کنید. در این آموزشِ ۱۵ دقیقه‌ای امکانات متلب برای محاسبات و عملیات بر روی اعداد مختلط و ترسیم ویژگی‌های مربوط به آنها ارائه شده است. همچنین، با استفاده از قواعد مربوط به ریشه‌گیری از اعداد مختلط، ریشه‌های چندگانه عدد یک، نمایش داده شده‌اند. سپس با تبدیل این روند به یک تابع، این موضوع به صورت تکرار شونده و برای چند عملیات ریشه‌گیری همزمان بحث شده است.
اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:
