انحراف میانگین — به زبان ساده

در مطالعه توزیع داده‌ها در یک جامعه آماری، مقداری که اندازه‌ها در اطراف آن توزیع شده‌اند را مقدار مرکزی می‌نامند و هر معیار عددی را که معرف مرکز مجموعه داده‌ها باشد، معیار گرایش به مرکز می‌نامند. میانگین و میانه از متداول‌ترین معیارهای گرایش به مرکز هستند. در واقع معدل فاصله هر عدد از میانگین مجموعه اعداد، برابر با انحراف میانگین (Mean Deviation) است. اگر دقت کرده باشید در جمله قبلی از کلمه «میانگین» دو بار استفاده کردیم: میانگین اعداد را پیدا کنید و از این میانگین، برای بدست آوردن فاصله هر عدد از میانگین استفاده کنید. سپس میانگین آن فاصله‌ها را به دست آورید!

ممکن است کمی پیچیده بنظر بیاید؛ اما تنها سه گام است:

1. میانگین تمامی مقادیر را به دست می‌آوریم.
2. فاصله هر مقدار را از آن میانگین به دست می‌آوریم (مقدار میانگین را از هر مقدار کم می‌کنیم و علامت‌های منفی را حذف می‌کنیم).
3. سپس میانگین این فاصله‌ها را به دست می‌آوریم.

فیلم آموزش ریاضی و آمار 1 – پایه دهم علوم انسانی در فرادرس

کلیک کنید

روش کار را در مثال زیر به صورت کامل توضیح داده‌ایم.

مثال: انحراف از میانگین اعداد زیر را پیدا می‌کنیم:

3, 6, 6, 7, 8, 11, 15, 16

مرحله اول: میانگین را پیدا کنید:

$${3 + 6+6 + 7 + 8 + 11 + 15 + 16 \over 8} = {72 \over 8} = 9$$

مرحله دوم: فاصله هر مقدار از میانگین را پیدا کنید:

که به این شکل است:

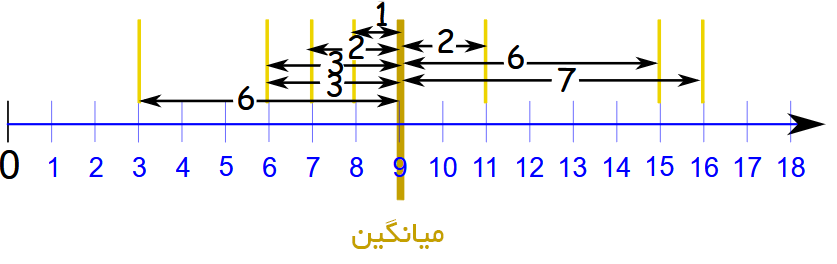
مرحله سوم: میانگین این فاصله‌ها را پیدا کنید:

$${6 + 3 + 3 + 2 + 1 + 2 + 6 + 7 \over 8 }= {30 \over 8} = 3.75$$

بدین ترتیب میانگین برابر 9 و انحراف میانگین برابر 3.75 است. انحراف میانگین، فاصله متوسط مقدار‌ها از وسط را برای ما مشخص می‌کند. پس در این مثال، مقادیر  به طور متوسط به اندازه 3.75 واحد از وسط دور هستند.

نکته: منظور از انحراف همان فاصله است.

فرمول

فرمول انحراف میانگین به صورت زیر است:

انحراف میانگین = $${Σ|x – μ| \over N}$$

فیلم آموزش آمار و احتمال – پایه یازدهم در فرادرس

کلیک کنید

در این فرمول:

• μ برابر میانگین است (در مثال برابر با 9 بود)
• x برابر عد مورد نظر است (مانند 3 یا 16)
• N برابر تعداد مقدارها است (در مثال 8 مقدار داشتیم)

انحراف مطلق

هر فاصله ای که ما محاسبه کردیم، «انحراف مطلق» (Absolute Deviation) نام دارد، چون که مقدار ثابت و مطلق (قدر مطلق) انحراف است (فاصله آن از میانگین). برای نشان دادن «قدر مطلق» از علامت (|) در طرفین اعداد استفاده می‌کنیم. مانند: 3 = | 3 –|

فیلم آموزش ریاضی 2 – پایه یازدهم علوم تجربی در فرادرس

کلیک کنید

برای هر مقدار x:

انحراف مطلق = | x – μ |

از مثال قبلی، مقدار 16، انحراف مطلق دارد:

| x – μ | = | 16 – 9 | = | 7 | = 7

اکنون تمامی مقدار های بدست آمده را جمع می‌کنیم.

سیگما

علامت «جمع کردن»، Σ است (به نام علامت سیگما)، پس داریم:

Σ | x – μ | = مجموع انحراف های مطلق

این رابطه را بر تعداد مقدار ها N تقسیم می‌کنیم و بنابراین انحراف میانگین برابر است با:

$${Σ|x – μ| \over N}$$

اکنون مثال قبلی را با علامت‌های درست خود حل می‌کنیم:

مثال: انحراف میانگین اعداد زیر را پیدا می‌کنیم:

3, 6, 6, 7, 8, 11, 15, 16

قدم اول: میانگین را بیابید:

$$μ = {3 + 6 + 6 + 7 + 8 + 11 + 15 + 16 \over 8} = {72 \over 8} = 9$$

قدم دوم: انحراف‌های مطلق را بیابید:

قدم سوم: انحراف میانگین را پیدا کنید:

$${Σ | x – μ | \over N} = {30 \over 8} = 3.75$$

به یاد داشته باشید که انحراف میانگین در پاره‌ای موارد با نام انحراف مطلق میانگین (MAD) استفاده می‌شود؛ چون که میانگین انحراف‌های مطلق است.

منظور از انحراف میانگین چیست؟

انحراف میانگین به ما فاصله متوسط تمامی مقادیر از وسط را نشان می‌دهد.

فیلم آموزش ریاضی و آمار 3 – پایه دوازدهم علوم انسانی در فرادرس

کلیک کنید

مثال: شما قد چند کودک را اندازه می‌گیرید (به سانتی متر):

مقدارهای به دست آمده بر حسب سانتی متر، به شکل زیر است:

102, 121, 142, 109, 118

گام اول: میانگین را پیدا کنید:

$$μ = {102 + 122 + 143 + 109 + 119 \over 5} = {595 \over 5} = 119$$

گام دوم: انحرافهای مطلق را پیدا کنید:

گام سوم: انحراف میانگین را پیدا کنید:

$${Σ | x – μ | \over N} ={ 54 \over 5} = 10.8$$

پس، به طور متوسط، قد کودکان از میانگین 10.8 سانتی متر فاصله دارند. آن را با انحراف معیار 13.96 سانتی متر مقایسه کنید.

یک بررسی سودمند

انحراف‌ها در یک طرف از میانگین باید با انحراف‌ها در طرف دیگر آن برابر باشند. در مثال اول داشتیم:

3, 6, 6, 7, 8, 11, 15, 16

انحراف‌ها به شکل زیر بوده است:

6 + 3 + 3 + 2 + 1 = 2 + 6 + 7

15 = 15

همچنین در مثال قد کودکان نیز موارد زیر را داشتیم:

• انحراف های سمت چپ برابر است با: 27 = 10 + 17
• انحراف های سمت راست برابر است با: 27 = 3 + 24

اگر این مقدارها برابر نباشند؛ احتمالاً اشتباهی مرتکب شده‌اید.

اگر این نوشته برای شما مفید بوده است، پیشنهاد می‌کنیم مطالب زیر را نیز ملاحظه کنید:

• مجموعه آموزش‌های ریاضی
• واریانس و انحراف معیار — به زبان ساده
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی
• متغیر های تصادفی – میانگین، واریانس و انحراف معیار – به زبان ساده
• مفاهیم آماری – شاخص‌های توصیفی
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی

==