فرادرساستقرای ریاضی — به زبان ساده
اگر به فرهنگ لغت فارسی مراجعه کنید و معنی واژه «استقرا» را جست‌وجو کنید، با چنین عباراتی روبه‌رو خواهید شد: «جزئیات را بررسی کردن و یک حکم کلی استخراج کردن؛ از جزء به کل رسیدن». این دقیقاً همان مفهومی است که در ما در ریاضیات و منطق با آن سروکار داریم. «استقرای ریاضی» (Mathematical Induction)، راهی برای اثبات گزاره‌های مربوط به اعداد طبیعی است که دو گام اصلی دارد:
- گام اول: اثبات درست بودن گزاره برای مورد یا عدد نخست
- گام دوم: اثبات اینکه «اگر گزاره برای هر مورد دیگر درست باشد، مورد بعدی هم صحیح است».
حتماً درباره «ویژگی دومینو» (Domino effect) شنیده‌اید که:
- مرحله اول: دومینوی اول می‌افتد.
- مرحله دوم: وقتی هر دومینویی بیفتد، دومینوی بعدی نیز می‌افتد.
بنابراین، همه دومینوها خواهند افتاد!
استقرای ریاضی یا استدلال استقرایی دقیقاً مشابه همین روند است. در دنیای اعداد، استقرای ریاضی به‌صورت زیر است:
- گام اول: نشان دهید که مورد اول صحیح است (معمولاً n=1).
- گام دوم: نشان دهید اگر n=k صحیح باشد، آن‌گاه n=k+1 نیز درست است.
چگونه استقرای ریاضی را انجام دهیم؟
گفتیم که استقرای ریاضی، دو گام دارد. گام اول ساده است؛ کافی است فقط ثابت کنیم مسئله مورد نظر برای n=1 صحیح است. بهترین راه برای انجام گام دوم، این‌گونه است:
- فرض کنید گزاره برای n=k صحیح است؛
- اثبات کنید گزاره برای n=k+1 صحیح است (می‌توانید از n=k به‌عنوان یک واقعیت یا قانون استفاده کنید).
انجام این کارها معادل این است که بگوییم «اگر توانایی انداختن یک دومینو را داشته باشیم، آیا می‌توانیم بعدی را نیز بیندازیم؟»
گام دوم را باید زیرکانه انجام دهیم. برای درک بهتر این موضوع، مثال زیر را مشاهده کنید.
مثال: آیا $$\boldsymbol{3^n-1}$$ ضریب 2 است؟
با استقرای ریاضی این موضوع را تحقیق می‌کنیم. به همان دو گام اصلی برمی‌گردیم که معرفی کردیم:
1. آیا این گزاره برای n=1 درست است؟
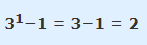
می‌بینیم که بله! 2 ضریب 2 و گزاره صحیح است.
2. این بار فرض کنیم گزاره برای n=k صحیح باشد؛ پس فرض می‌کنیم عبارت زیر ضریب ۲ است.
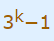
دقت کنید ما فقط فرض کرده‌ایم $$3^k-1$$ ضریب 2 است و از آن به‌عنوان یک واقعیت استفاده می‌کنیم.
اکنون باید بررسی کنیم که با فرض بالا، آیا $$3^{k+1}-1$$ ضریب 2 هست یا خیر. عبارت $$3^{k+1}$$ به‌صورت $$3\times 3^k$$ قابل تفکیک است. بخش «$$3\times$$» این عبارت را می‌توان به‌صورت مجموع «$$2\times$$» و «$$1\times$$» بیان کرد. بنابراین، داریم:
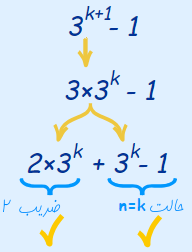
واضح است که $$2\times 3^k$$ ضریب 2 است و قبلاً هم فرض کردیم که $$3^k-1$$ مضربی از آن است. بنابراین عبارت زیر ضریب 2 است و اثبات صحت گزاره انجام شد.
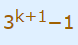
شاید بپرسید چرا در فرایند اثبات، $$3^k-1$$ را مضرب 2 فرض کردیم و دلیلی برای آن نیاوردیم؟ پاسخ این است که بر «ویژگی دومینو» تکیه کردیم. ما با این کار پرسیدیم اگر هر کدام از دومینوها بیفتد آیا دومینوی بعد از آن هم می‌افتد؟
به همین خاطر موقتاً به‌عنوان یک واقعیت پذیرفتیم دومینوی «n=k» می‌افتد (یعنی $$3^k-1$$ مضرب 2 است) و دیدیم که دومینوی «n=k+1» نیز خواهد افتاد و گزاره را اثبات کردیم.
قبلاً گفتیم گاهی با مسائلی برخورد می‌کنیم که باید زیرکانه با آن‌ها برخورد کنیم. در دو مثال زیر می‌توانید نحوه اثبات صحت عبارت‌های مربوط به n=k+1 را ببینید.
مثال: مجموع مربع اعداد فرد
سری زیر را در نظر بگیرید که مجموع اعداد طبیعی فرد است:
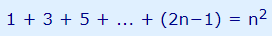
می‌خواهیم اثبات کنیم حاصل جمع این اعداد برابر $$n^2$$ است و رابطه بالا درست است.
حل:
1. ابتدا ثابت می‌کنیم این عبارت برای n=1 صحیح است:
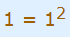
می‌بینیم که تساوی برای n=1 برقرار است.
2. فرض می‌کنیم تساوی داده شده برای n=k درست باشد؛ یعنی:
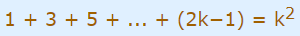
اکنون باید اثبات کنیم که عبارت داده شده برای «k+1» درست است:
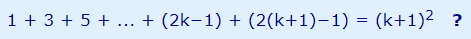
می‌دانیم که $$1+3+5+...+(2k-1)=k^2$$ (فرض قسمت 2)، با جایگذاری k+1 داریم:
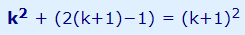
اگر همه جملات را بسط دهیم، به عبارت زیر می‌رسیم:
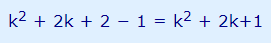
و به‌طور ساده‌تر:
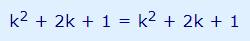
دو طرف تساوی برابر است. در نتیجه عبارت زیر درست است.
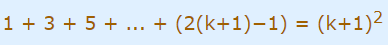
با هم دو مثال دیگر را بررسی می‌کنیم.
مثال: اعداد مثلثی
دنباله اعداد مثلثی زیر را در نظر بگیرید:
اثبات کنید nاُمین عدد مثلثی برابر است با:
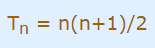
حل:
1. ابتدا درستی گزاره را برای n=1 تحقیق می‌کنیم که درست است:
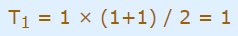
2. فرض می‌کنیم عبارت برای n=k صحیح باشد، پس رابطه زیر درست است (فرض!).
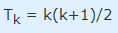
اکنون صحت عبارت را برای k+1 بررسی می‌کنیم:
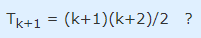
طبق فرض می‌دانیم $$T_k=k(k+1)/2$$. مقدار $$T_{k+1}$$ یک ردیف $$(k+1)$$تایی به نقطه‌ها می‌افزاید. بنابراین $$T_{k+1}=T_k+(k+1)$$ و
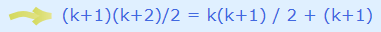
با ضرب همه جملات در 2 داریم:
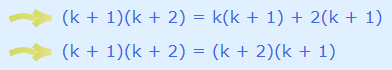
می‌بینیم که دو طرف معادله برابر است و در نتیجه عبارت زیر درست است:
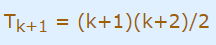
بدین ترتیب، اثبات انجام شده است.
مثال: جمع مکعب اعداد
ثابت کنید رابطه زیر برقرار است:
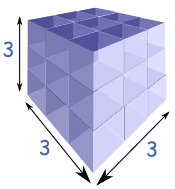
حل:
1. ابتدا باید ثابت کنیم عبارت برای n=1 درست است:
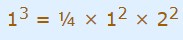
2. فرض می‌کنیم رابطه برای n=k برقرار باشد:
اکنون باید ثابت کنیم فرمول ارائه شده برای «k+1» درست است:
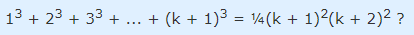
طبق فرض بند 2، می‌دانیم $$1^3+2^3+3^3+...+k^3=1/4k^2(k+1)^2$$، بنابراین می‌توانیم بنویسیم:
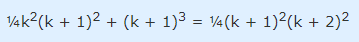
با ضرب طرفین در عدد 4 داریم:
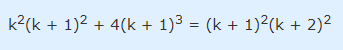
تمام جملات دو طرف تساوی بالا، ضریب مشترک $$(k+1)^2$$ دارند. با حذف این عامل، به تساوی ساده شده زیر می‌رسیم:
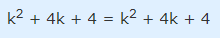
دو طرف تساوی برابرند و بنابراین عبارت زیر درست است:
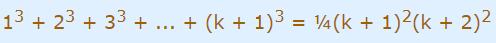
در نتیجه اثبات انجام شده است.
از مزیت‌های استدلال به کمک استقرای ریاضی، گام به گام بودن آن و عدم نیاز به بینش گسترده است. اما از آن‌جایی که استدلال استقرایی مختص حوزه اعداد طبیعی است، محدودیت دارد و می‌توان گفت برای اثبات نتایجی به‌کار می‌رود که آن‌ها را حدس می‌زنیم اثبات شده‌اند.
اگر علاقه‌مند به سایر موضوعات مشابه مطالب بالا هستید، پیشنهاد می‌کنیم آموزش‌های زیر را نیز ببینید:
- مجموعه آموزش‌های ریاضیات
- مجموعه آموزش‌های ریاضی و فیزیک
- مجموعه آموزش‌های دبیرستان و پیش‌دانشگاهی
- فهرست مطالب ریاضی وبلاگ فرادرس
- منطق و تعمیم — آیا تعمیم غیر منطقی همیشه اشتباه است؟
- اعداد حقیقی — به زبان ساده
^^
سلام لطفا علاوه بر مثال های اثبات های بوسیله قضیه استقرای ریاضی اثبات خود قضیه رو هم در مطلب قرار بدید.
عالی بود واقعا .ممنون
این سوال با استقرا چطوری حل میشه:
ثابت کنید
(پنج به توان( دو ان به علاوه سه )) به علاوه (دو به توان ان)(سه به توان (ان به علاوه سه))
همیشه اول است
ریاضی نمیشه نوشت
واقعا عالی خیلی ممنون از شما
سلام مرتضی عزیز.
از اینکه این آموزش مجله فرادرس برایتان مفید بوده، بسیار خوشحالیم.
شاد و سربلند باشید.
واقعا ممنونم از ویدیو های بسیار عالی و کاربردی تون.
عالی بود واقعا هرکاری میکردم یاد نمیگرفتم خیلییی خوب توضیح دادین مرسی🤍
خیلی ساده و سریع یادگرفتم. ممنون از شما
سلام لطفا میشه اثبات فرمول دنباله هندسی را به کمک استقرا حل کنید
سلام… حدث یا حدس؟؟
مطالبتون واقعا عالیه ولی کاش یکم صریح تر میگفتید البته من کمی شو متوجه شدم . به هر حال سپاس فراوان
سلام.
اشتباه تایپی تصحیح شد.
از توجه شما سپاس‌گزاریم.
سلام ، من یه سوال درباره ی دنباله های استقرایی فصل اول ریاضی پایه داشتم ، آقای حمیدی اینستاگرام دارن عکس رو براشون ارسال کنم؟