تزویج در مدارهای الکتریکی – مفاهیم اصلی (+ دانلود فیلم آموزش رایگان)

وقتی جریان متغیری از یک سیم‌پیچ عبور کند، در اطراف آن، شار مغناطیسی ایجاد می‌شود. اگر سیم‌پیچ دیگری در مجاورت سیم‌پیچ نخست قرار گیرد، به‌گونه‌ای که شار از آن بگذرد، ولتاژی در سیم‌پیچ دوم القا می‌شود که با تغییرات جریان سیم‌پیچ اول متناسب است. در این حالت، می‌گوییم دو سیم‌پیچ تزویج مغناطیسی دارند. ترانسفورماتور، یکی از تجهیزاتی است که بر اساس همین تزویج در مدار، طراحی شده و کاربردهای فراوانی در صنعت برق و الکترونیک دارد. در این آموزش، تزویج در مدارهای الکتریکی را معرفی خواهیم کرد.

اندوکتانس متقابل

وقتی دو سلف یا سیم‌پیچ در مجاورت یک‌دیگر قرار گیرند و جریان از یک سیم‌پیچ عبور کند، شار مغناطیسی در سیم‌پیچ‌ها تولید خواهد شد.

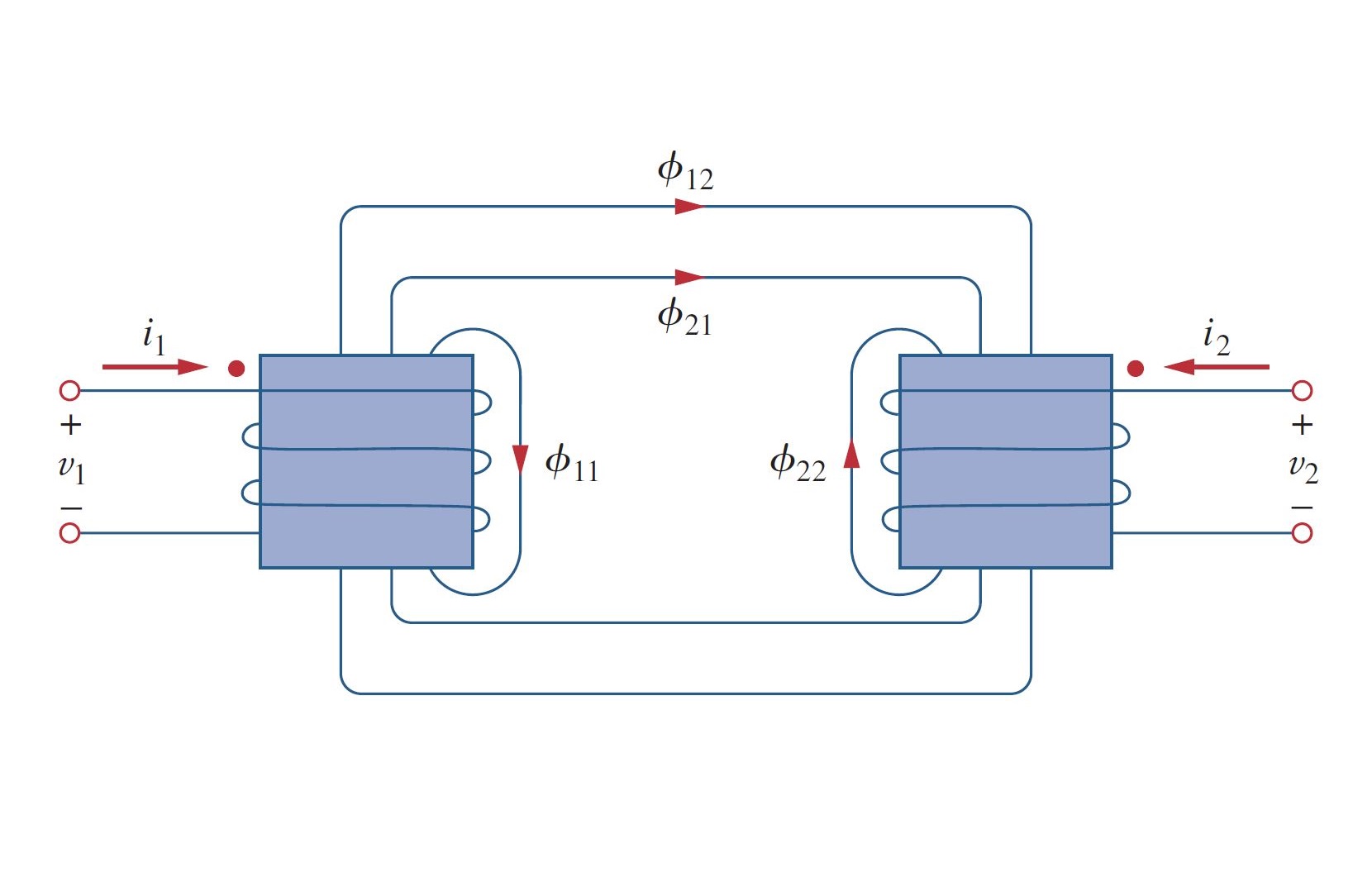
ابتدا یک سلف سیم‌پیچی شده را با $$N$$ دور در نظر بگیرید. وقتی جریان $$i$$ از سیم‌پیچی بگذرد، شار مغناطیسی $$\phi$$ در اطراف تولید خواهد شد (شکل 1).

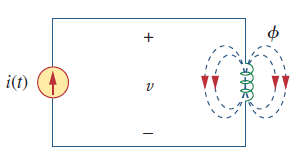
براساس قانون فارادی، ولتاژ القا شده سیم‌پیچ ($$v$$)، با تعداد دورهای $$N$$ و نرخ تغییر شار مغناطیسی $$\phi$$ متناسب است. یعنی:

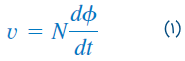
اما شار $$\phi$$ با جریان $$i$$ تولید می‌شود، بنابراین هر تغییر در $$\phi$$ به‌علت تغییر در جریان ایجاد می‌شود. در نتیجه، معادله (۱) را می‌توان به‌صورت زیر بازنویسی کرد:

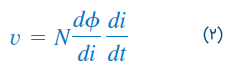
یا

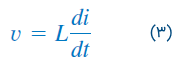
که رابطه ولتاژ-جریان سلف را بیان می‌کند. از معادلات (۲) و (۳)، مقدار اندوکتانس $$L$$ سلف را می‌توان به‌صورت زیر بیان کرد:

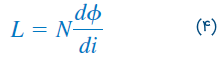
این اندوکتانس، معمولاً «اندوکتانس خودی» (Self-inductance) نامیده می‌شود، زیرا ولتاژ القا شده در سیم‌پیچ، با جریان متغیر همان سیم‌پیچ ایجاد شده است.

اکنون، دو سیم‌پیچ را با اندوکتانس خودی $$L_1$$ و $$L_2$$ در نظر بگیرید که نزدیک یک‌دیگر هستند (شکل 2).

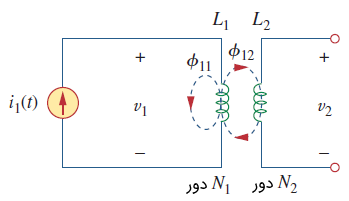
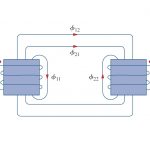
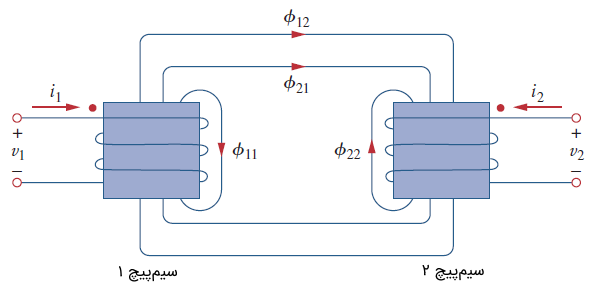
تعداد دور سیم‌پیچ‌های ۱ و ۲، به‌ترتیب، برابر با $$N_1$$ و $$N_2$$ است. برای سادگی فرض کنید در سلف دوم جریانی برقرار نیست. شار مغناطیسی $$\phi _1$$ که از سیم‌پیچ ۱ نشئت می‌گیرد، دو مولفه دارد؛ مولفه $$\phi _{11}$$ که فقط از سیم‌پیچ 1 عبور می‌کند و مولفه $$\phi _{12}$$ که هر دو سیم‌پیچ را احاطه می‌کند. بنابراین،

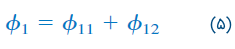
اگرچه دو سیم‌پیچ از نظر فیزیکی مجزا هستند، اما از نظر مغناطیسی تزویج دارند. از آن‌جایی که شار کل $$\phi _1$$ در سیم‌پیچ ۱ حلقه می‌بندد، ولتاژ القا شده در سیم‌پیچ ۱ برابر است با

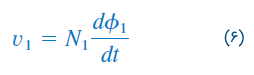
خطوط شار $$\phi _{12}$$، از سیم‌پیچ ۲ می‌گذرند، بنابراین، ولتاژ القا شده در سیم‌پیچ 2 از رابطه زیر به‌دست می‌آید:

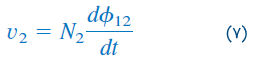
چون شارها، با عبور جریان $$i_1$$ از سیم‌پیچ ۱ ایجاد شده‌اند، رابطه (۶)‌ را می‌توان به‌صورت زیر بازنویسی کرد:

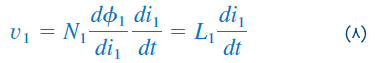
که در آن، $$L_1=N_1 d\phi _1/di_1$$ مقدار اندوکتانس خودی سیم‌پیچ 1 است. به‌طریق مشابه، معادله (۷) را می‌توان به‌صورت زیر نوشت:

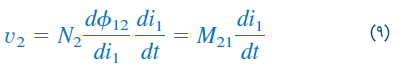
که در آن:

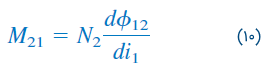
مقدار $$M_{21}$$، «اندوکتانس متقابل» (Mutual inductance) یا اندوکتانس تزویج سیم‌پیچ ۲ نسبت به سیم‌پیچ ۱ نامیده می‌شود. اندیس 21 نشان می‌دهد که اندوکتانس $$M_{21}$$، ولتاژ القایی سیم‌پیچ ۲ را به جریان سیم‌پیچ ۱ مرتبط می‌کند. بنابراین، ولتاژ متقابل (یا ولتاژ القایی) مدار باز سیم‌پیچ ۲ برابر است با:

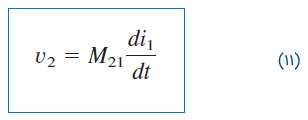
اکنون فرض کنید جریان $$i_2$$ در سیم‌پیچ ۲ برقرار شود، در حالی که از سیم‌پیچ ۱ جریانی عبور نکند (شکل 3). شار $$\phi _2$$ از سیم‌پیچ ۲ ناشی می‌شود. شار $$\phi _{22}$$‌ در سیم‌پیچ ۲ و $$\phi _{21}$$ در هر دو سیم‌پیچ برقرار است. بنابراین:

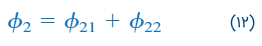
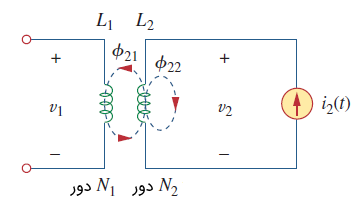
شار کل $$\phi _2$$، در سیم‌پیچ 2 حلقه می‌بندد، بنابراین ولتاژ‌ القایی سیم‌پیچ ۲ برابر با رابطه زیر است:

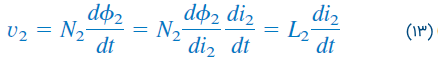
که در آن، $$L_2=N_2 d\phi _2/di_2$$ اندوکتانس خودی سیم‌پیچ ۲ است. از آن‌جایی که شار $$\phi _{21}$$ از سیم‌پیچ ۱ می‌گذرد، ولتاژ القایی آن با رابطه زیر به‌دست می‌آید:

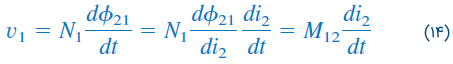
که در آن:

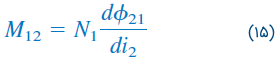
مقدار بالا، اندوکتانس متقابل سیم‌پیچ ۱ نسبت به سیم‌پیچ ۲ نامیده می‌شود. بنابراین، ولتاژ‌ متقابل مدار باز سیم‌پیچ ۱ برابر است با:

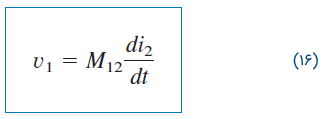
مقدار اندوکتانس‌های متقابل با هم برابر است:

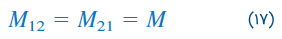
$$M$$، اندوکتانس متقابل بین دو سیم‌پیچ است. مشابه امپدانس خودی $$L$$، امپدانس متقابل $$M$$ برحسب هانری (H) اندازه‌گیری می‌شود. به یاد داشته باشید که تزویج متقابل تنها زمانی وجود خواهد داشت که سلف‌ها یا سیم‌پیچ‌ها در نزدیکی هم باشند و مدار با منابع متغیر با زمان تغذیه شود. سلف‌ها در حالت dc مانند اتصال کوتاه عمل می‌کنند.

از دو شکل 2 و ۳ می‌توان نتیجه گرفت اندوکتانس متقابل زمانی وجود خواهد داشت که ولتاژ، ناشی از جریان متغیر مدار دیگر القا شود. بنابراین: اندوکتانس متقابل، توانایی سلف برای القای ولتاژ بر سلف مجاورش است که برحسب هانری (H) بیان می‌شود.

قرارداد نقطه‌گذاری

اگرچه اندوکتانس متقابل $$M$$ همیشه مثبت است، ولتاژ متقابل $$M di/dt$$ مانند ولتاژ خودالقایی $$L di/dt$$ ممکن است مثبت یا منفی باشد. البته، برخلاف ولتاژ خودالقایی $$L di/dt$$ که پلاریته آن با جهت مرجع جریان و پلاریته مرجع ولتاژ (براساس جهت قراردادی) مشخص می‌شود، تعیین پلاریته ولتاژ متقابل $$Mdi/dt$$ کار ساده‌ای نیست. زیرا در این حالت چهار سر (ترمینال) وجود دارد.

فیلم آموزش مدارهای الکتریکی ۲ – حل تمرین در فرادرس

کلیک کنید

انتخاب پلاریته صحیح $$Mdi/dt$$ با اعمال قانون لنز و دست راست به دو سیم‌پیچ تعیین می‌شود. از آن‌جایی که نشان دادن جزئیات ساختار سیم‌پیچ واقعی آسان نیست، از «قرارداد نقطه» (Dot convention) در تحلیل مدار استفاده می‌کنیم. با این قرارداد، یک نقطه در یکی از سرهای هر سیم‌پیچ مشخص می‌شود. این موضوع، در شکل 4 نشان داده شده است. نقاط، از قبل کنار سیم‌پیچ‌ها مشخص می‌شوند، بنابراین نیازی نیست ما آن‌ها را تعیین کنیم. از نقطه‌ها برای تعیین پلاریته ولتاژ متقابل استفاده می‌شود.

قرارداد نقطه به این صورت بیان می‌شود: اگر جریان به سر نقطه‌دار یک سیم‌پیچ وارد شود، پلاریته مرجع ولتاژ متقابل در سیم‌پیچ دوم، در سر نقطه‌دار سیم‌پیچ، مثبت است.

به بیان مشابه: اگر جریان از سر نقطه‌دار یک سیم‌پیچ خارج شود، پلاریته مرجع ولتاژ متقابل در سیم‌پیچ دوم، در سر نقطه‌دار سیم‌پیچ، منفی است.

بنابراین، پلاریته مرجع ولتاژ متقابل، به جهت مرجع جریان القاکننده و نقطه سیم‌پیچ‌های تزویج شده بستگی دارد. نحوه استفاده از قانون نقطه، در شکل 5 برای چهار مدار تزویج نشان داده شده است.

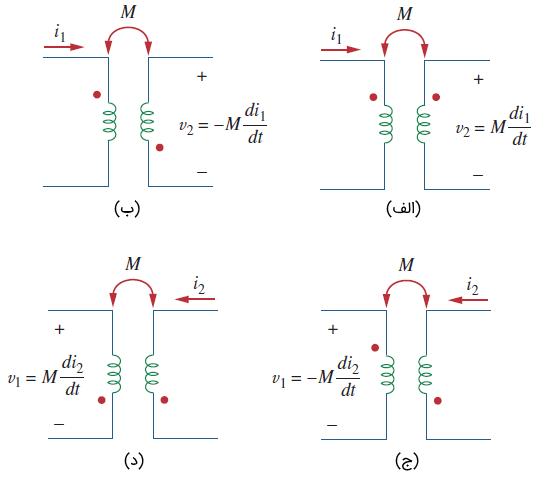
علامت ولتاژ متقابل $$v_2$$ در سیم‌پیچ‌های مزدوج شکل 5 (الف)،‌ با پلاریته مرجع $$v_2$$ و جهت $$i_1$$ تعیین می‌شود. از آن‌جایی که $$i_1$$‌ وارد سر نقطه‌دار سیم‌پیچ ۱ می‌شود و $$v_2$$ در سر نقطه‌دار سیم‌پیچ ۲ مثبت است، ولتاژ متقابل برابر است با $$+Mdi_1/dt$$. برای سیم‌پیچ‌های شکل 5 (ب)، جریان $$i_1$$‌ به سر نقطه‌دار سیم‌پیچ ۱ وارد می‌شود و $$v_2$$ در سر نقطه‌دار سیم‌پیچ ۲ منفی است. بنابراین، ولتاژ‌ متقابل برابر است با $$-M di_1/dt$$.

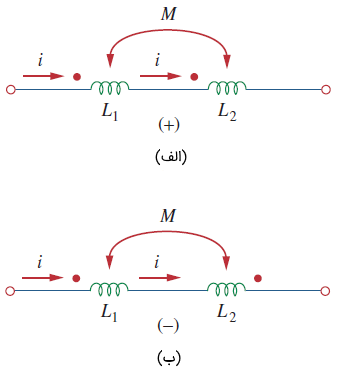
شکل 6، نقطه‌گذاری سیم‌پیچ‌های تزویج شده سری را نشان می‌دهد. اندوکتانس کل سیم‌پیچ‌های شکل ۶ (الف) برابر است با:

برای سیم‌پیچ‌های شکل 6 (ب) داریم:

تحلیل مدار دارای تزویج

اکنون که می‌دانیم چگونه پلاریته ولتاژ‌ متقابل را تعیین کنیم، تحلیل مدارهای شامل اندوکتانس متقابل را بررسی می‌کنیم.

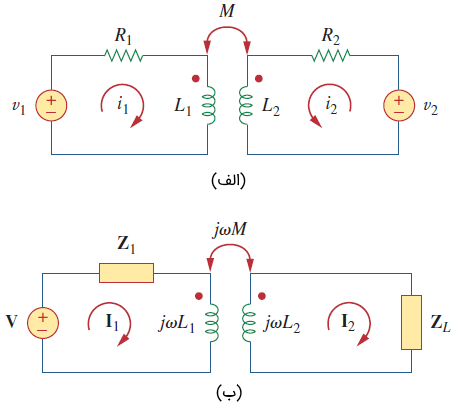
به‌عنوان مثال، مدار شکل ۷ (الف) را در نظر بگیرید. با اعمال KVL به سیم‌پیچ ۱، داریم:

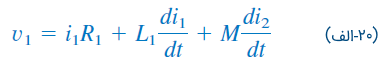
به‌طریق مشابه، برای سیم‌پیچ ۲ می‌توان نوشت:

معادله (20) را می‌توان در فضای فرکانس به‌صورت زیر بیان کرد:

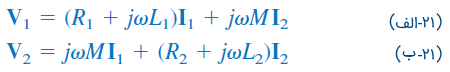
اکنون، مدار شکل 7 (ب) را در نظر بگیرید. معادله KVL در فضای فرکانس برای سیم‌پیچ ۱ به‌صورت زیر است:

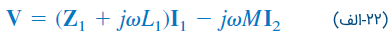
برای سیم‌پیچ 2 نیز داریم:

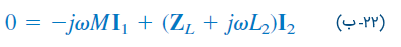
معادلات (21) و (22) را می‌توان طبق روش‌های متداول تحلیل مدار حل کرد.

یکی از مهم‌ترین چیزهایی که سبب می‌شود از حل دقیق مسئله مطمئن شویم، بررسی هر مرحله طی فرایند حل و تایید صحت فرضیات است. در حل مدارهای تزویج نیز باید علامت و مقدار ولتاژ القایی متقابل بررسی شود. با استفاده از مدل شکل 8 (ب) می‌توان تحلیل تزویج (شکل 8 (الف)) را در مدارهای الکتریکی ساده‌تر کرد.

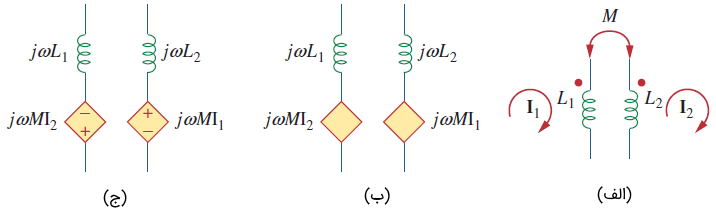
البته باید علامت منابع نشان داده شده در شکل 8 (ب)‌ را تعیین کرد. واضح است که $$I_1$$ ولتاژ $$j \omega M I_1$$ را در سیم‌پیچ دوم و $$I_2$$، ولتاژ $$j \omega M I_2$$ را در سیم‌پیچ اول القا می‌کند. از آن‌جایی که $$I_1$$ وارد سر نقطه‌دار $$L_1$$ می‌شود، ولتاژی در $$L_2$$ القا می‌کند که سعی می‌کند جریانی از سر نقطه‌دار $$L_2$$ بکشد، بنابراین، قسمت بالای منبع باید علامت مثبت داشته باشد. جریان $$I_2$$ از سر نقطه‌دار $$L_2$$ خارج می‌شود و ولتاژی را در $$L_1$$ القا می‌کند که تلاش می‌کند جریان را به سر نقطه‌دار $$L_1$$ وارد کند. بنابراین، قسمت بالای منبع وابسته باید منفی و پایین آن مثبت باشد. شکل ۸ (ج)، مدار معادل نهایی مدار تزویج را نشان می‌دهد.

انرژی در مدارهای تزویج

همان‌گونه که می‌دانیم، انرژی ذخیره شده در یک سلف، با رابطه زیر بیان می‌شود:

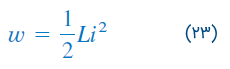
اکنون می‌خواهیم انرژی ذخیره شده در سیم‌پیچ‌های تزویج مغناطیسی را پیدا کنیم. مدار شکل 9 را در نظر بگیرید. فرض می‌کنیم شرایطه اولیه جریان‌های $$i_1$$ و $$i_2$$ و بنابراین انرژی ذخیره شده در سیم‌پیچ‌ها، صفر است. اگر اجازه دهیم جریان $$i_1$$ از مقدار صفر به $$I_1$$ افزایش پیدا کند، در حالی که $$i_2=0$$‌ باشد، توان سیم‌پیچ ۱ برابر است با

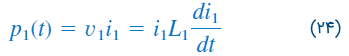
و انرژی ذخیره شده در مدار، از رابطه زیر به‌دست می‌آید:

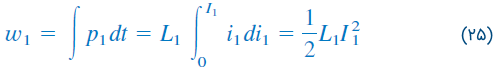
اگر مقدار $$i_1=I_1$$‌ را نگه داریم و $$i_2$$ را از صفر به $$I_2$$ افزایش دهیم، ولتاژ متقابل القایی در سیم‌پیچ ۱، برابر با $$M_{12} di_2/dt$$ خواهد بود، در حالی که ولتاژ متقابل القایی در سیم‌پیچ ۲ به دلیل عدم تغییر $$i_1$$، صفر است. بنابراین، توان سیم‌پیچ‌ها را می‌توان به‌صورت زیر نوشت:

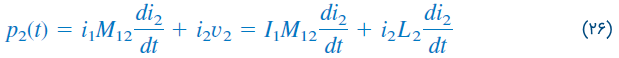
و انرژی ذخیره شده مدار را از رابطه زیر به‌دست آورد:

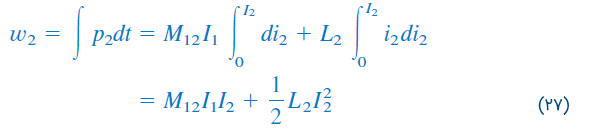
انرژی کل ذخیره شده در سیم‌پیچ‌ها وقتی هر دو جریان $$i_1$$ و $$i_2$$ به مقادیر ثابتی می‌رسند، برابر است با:

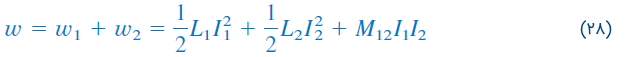
اگر ابتدا $$i_2$$ را از صفر به $$I_2$$ افزایش دهیم، سپس $$i_1$$ را از صفر تا $$I_1$$‌ زیاد کنیم، انرژی کل ذخیره شده در سیم‌پیچ‌ها را می‌توان با رابطه زیر محاسبه کرد:

از آن‌جایی که انرژی کل ذخیره شده، صرف‌نظر از نحوه رسیدن به شرایط نهایی باید مشابه باشد، با مقایسه معادلات (28) و (۲۹)، داریم:

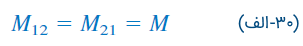
و

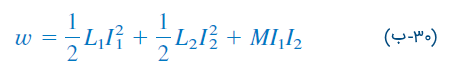
معادله فوق، براساس این فرض به‌دست آمده که جریان‌های سیم پیچ به سرهای نقطه‌دار وارد می‌شوند. اگر یک جریان به سر نقطه‌دار وارد و دیگری از سر نقطه‌دار خارج شود، ولتاژ متقابل و در نتیجه انرژی متقابل $$MI_1I_2$$ منفی خواهند بود. در این حالت:

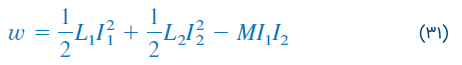
همچنین، از آن‌جایی که $$I_1$$ و $$I_2$$ مقادیری اختیاری هستند، می‌توان آن‌ها را به ترتیب، با $$i_1$$ و $$i_2$$ جایگزین کرد. در نتیجه، انرژی ذخیره شده لحظه‌ای مدار در حالت کلی برابر است با:

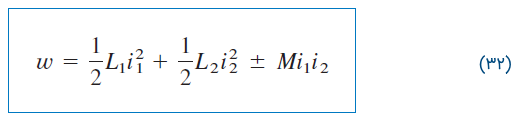
در رابطه بالا، علامت مثبت برای حالتی است که هر دو جریان، به سرهای نقطه‌دار سیم‌پیچ‌ها وارد یا از آن‌ها خارج شوند. علامت منفی نیز برای عکس این موارد است.

اکنون کران بالا یا حداکثر مقدار اندوکتانس متقابل $$M$$‌ را تعیین می‌کنیم. انرژی ذخیره شده در مدار نمی‌تواند منفی باشد، زیرا مدار، پسیو است. این یعنی مقدار $$1/2L_1i_1^2+1/2L_2i_2^2-Mi_1i_2$$ باید بزرگ‌تر یا مساوی صفر باشد:

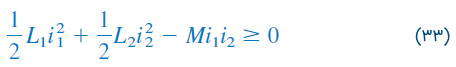
با اضافه و کم کردن مقادیر $$i_1i_2\sqrt{L_1L_2}$$ در سمت راست رابطه (۳۳)، می‌توان آن را به‌صورت زیر بازنویسی کرد:

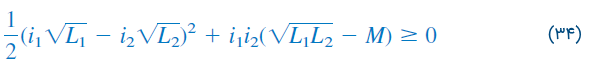
جمله مربع هیچ‌گاه نمی‌تواند منفی باشد و حداقل مقدار آن صفر است. بنابراین، جمله دوم سمت راست نامعادله (34) باید بزرگ‌تر از صفر باشد. در نتیجه:

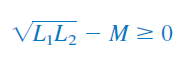
یا

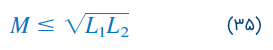
بنابراین، مقدار اندوکتانس متقابل نمی‌تواند بزرگ‌تر از میانگین هندسی اندوکتانس‌های خودی سیم‌پیچ‌ها باشد. برای آنکه نسبت مقدار اندوکتانس متقابل $$M$$ به حداکثر مقدار آن را بدانیم، ضریب تزویج $$k$$‌ را به‌صورت زیر تعریف می‌کنیم:

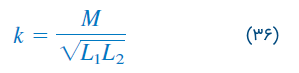
یا

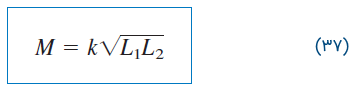
که در آن، $$0 \le k \le 1$$‌ یا معادل آن، $$0\le M \le \sqrt{L_1L_2}$$. ضریب تزویج را می‌توان به‌صورت نسبت شار نیز نوشت:

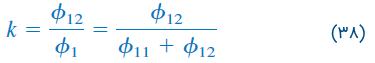
و

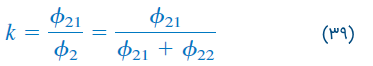
اگر شار کل تولیدی یک سیم‌پیچ، از سیم‌پیچ دیگر بگذرد، آن‌گاه $$k=1$$ و 100 درصد تزویج داریم، به عبارت دیگر، سیم‌پیچ‌ها کاملاً تزویج دارند. همچنین، اگر $$k<0.5$$، سیم‌پیچ‌ها تزویج ضعیف و اگر $$k>0.5$$، سیم‌پیچ‌ها تزویج قوی دارند.

ضریب تزویج $$k$$، معیاری برای تزویج مغناطیسی بین دو سیم‌پیچ است؛ $$0 \le k \le1$$.

ضریب $$k$$، به میزان نزدیکی، جنس هسته، جهت و و نوع سیم‌پیچ‌ها بستگی دارد.

در صورتی که مباحث بیان شده برای شما مفید بوده و می‌خواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد می‌کنیم به آموزش‌های زیر مراجعه کنید:

• تقویت کننده های الکترونیکی — مجموعه مقالات جامع وبلاگ فرادرس
• دو قطبی در مدارهای الکتریکی — به زبان ساده

^^