خطی سازی سیستم های غیرخطی — از صفر تا صد (+ دانلود فیلم آموزش گام به گام)

قوانین خطی ولتاژ برحسب جریان در مقاومت‌ها، نیرو برحسب جابه‌جایی در فنرها، نیرو برحسب سرعت برای اصطکاک و امثال این موارد، تنها تقریب‌هایی از روابط غیرخطی پیچیده‌تر هستند. از آن‌جایی که سیستم‌های خطی از این قاعده مستثنی نیستند، دسته دیگری از سیستم‌ها برای مطالعه وجود دارد که با معادلات دیفرانسیل غیرخطی تعریف می‌شوند. در این آموزش، نحوه به‌دست آوردن تقریب خطی سیستم‌های غیرخطی را برای محاسبه توابع تبدیل بررسی خواهیم کرد.

گام نخست، شناخت مولفه‌های غیرخطی و نوشتن معادلات دیفرانسل غیرخطی سیستم است. وقتی یک معادله دیفرانسیل غیرخطی را خطی می‌کنیم، در واقع، خطی‌سازی را برای ورودی‌های سیگنال کوچک حول پاسخ حالت ماندگار (وقتی ورودی صفر باشد) انجام می‌دهیم. این پاسخ حالت ماندگار، «تعادل» (Equilibrium) نامیده می‌شود و یافتن آن، گام دوم در فرایند خطی‌سازی است. برای مثال، وقتی یک پاندول مدت زیادی ساکن و بدون حرکت باشد، می‌گوییم در حالت تعادل است. جابه‌جایی زاویه‌ای این پاندول، با یک معادله دیفرانسیل غیرخطی بیان می‌شود، اما می‌توان آن را برای تغییرات کوچک حول نقطه تعادل، با معادله دیفرانسیل خطی توصیف کرد. در مرحله سوم، باید معادله دیفرانسیل غیرخطی را خطی کنیم.

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

دلیل اهمیت مدل خطی این است که طراح اغلب می‌تواند از یک تقریب خطی برای یک سیستم غیرخطی استفاده کند. تقریب خطی، تحلیل و طراحی سیستم را آسان می‌کند و نتایج مناسبی دارد که به واقعیت نزدیک است. مثلاً اگر مقادیر ورودی برای نقطه‌ای روی منحنی غیرخطی، در بازه کوچکی تغییر کنند، می‌توان یک رابطه خطی ارائه کرد که آن نقطه،‌ مبدا سیستم خطی محسوب می‌شود.

فرایند خطی‌سازی که این‌جا بیان می‌کنیم، مبتنی بر بسط سری تیلور تابع غیرخطی حول نقطه کار یا همان نقطه تعادل سیستم است. از آن‌جایی که در بسط سری تیلور، از جملات مرتبه بالا صرف‌نظر می‌کنیم، این جملات باید به‌اندازه کافی کوچک باشند؛ به این معنی که متغیرها تغییرات کوچکی حول نقطه کار داشته باشند.

گفتیم که اولین گام در خطی‌سازی، شناخت اجزای غیرخطی و نوشتن معادلات دیفرانسیل غیرخطی است.

وقتی یک معادله دیفرانسیل غیرخطی را خطی می‌کنیم، در حقیقت، آن را برای ورودی‌های سیگنال‌کوچک حول حالت ماندگار (پاسخ حالت صفر) خطی می‌کنیم. این مقدار ماندگار، تعادل نامیده می‌شود و در فرایند خطی‌سازی از آن استفاده می‌کنیم.

در مرحله بعدی، باید معادله دیفرانسیل غیرخطی را خطی کنیم. برای تعیین تابع تبدیل سیستم، می‌توانیم از معادله دیفرانسیل خطی در شرایط اولیه صفر تبدیل لاپلاس بگیریم.

ابتدا خطی‌سازی یک تابع را در نظر بگیرید.

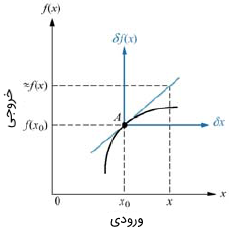
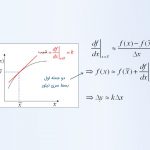
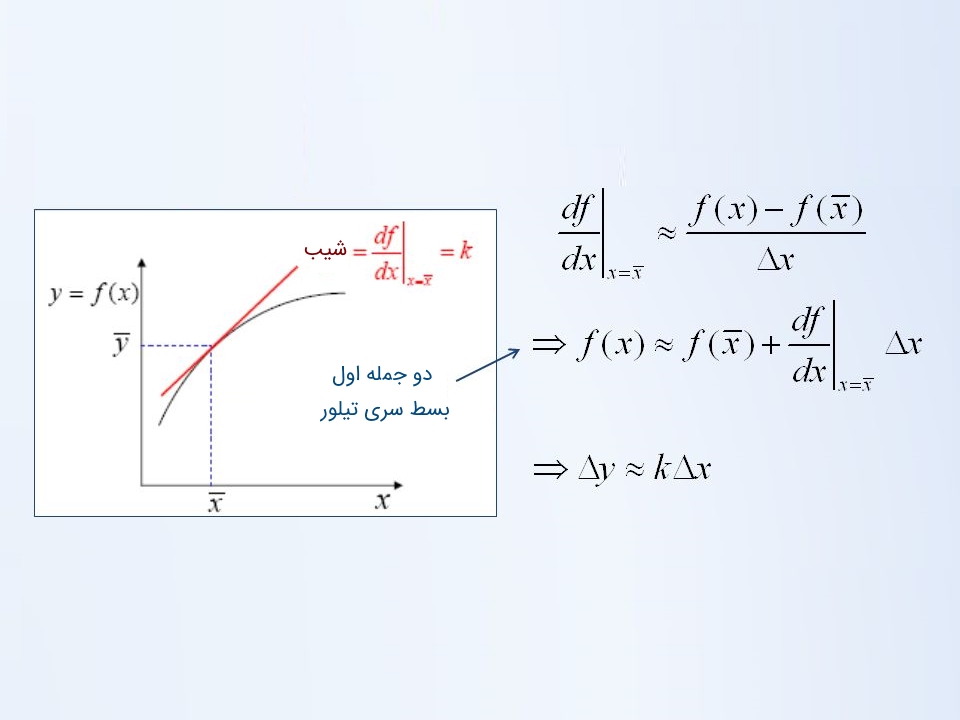
اگر فرض کنیم یک سیستم غیرخطی در نقطه $$(x_0, f(x_0))$$ کار می‌کند، تغییرات کوچک ورودی و تغییرات خروجی را می‌توان توسط شیب در نقطه A مرتبط کرد. بنابراین، اگر شیب منحنی در نقطه A برابر با $$m_a$$ باشد، تغییرات کوچک ورودی حول نقطه A (یعنی $$\delta x$$)،‌ سبب تغیرات کوچک در خروجی (یعنی $$\delta f(x)$$) می‌شود و می‌توان آن‌ها را با شیب در نقطه A به یک‌دیگر مرتبط کرد:

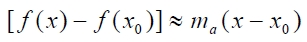
که:

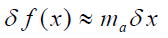
و

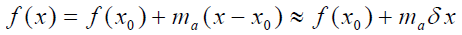
این رابطه، به‌صورت گرافیکی در شکل ۱ نشان داده شده است.

مثال ۱

تابع $$f(x)= 5 \cos x$$ را حول $$x=x_0=\frac{\pi}{2}$$ خطی کنید.

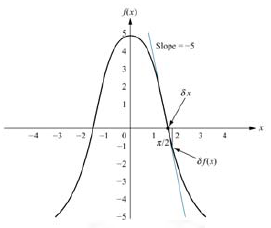
حل: ابتدا مشتق $$f(x)$$ را محاسبه می‌کنیم که برابر است با $$df/dx=-5 \sin x$$. در نقطه داده شده، مقدار مشتق برابر با $$-5$$ است. همچنین در این نقطه، $$f(x_0)=0$$ است. طبق رابطه (۱)، می‌توان سیستم را به‌صورت $$f(x)=-5 \delta x$$ برای تغییرات کوچک اطراف $$\pi /2$$ در نظر گرفت.

استفاده از سری تیلور

بحث بالا را می‌توان با استفاده از بسط سری تیلور بیان کرد که مقدار یک تابع را براساس مقدار آن در یک نقطه خاص و مشتقات ارائه می‌کند:

فیلم آموزش کنترل خطی با رویکرد حل مساله در فرادرس

کلیک کنید

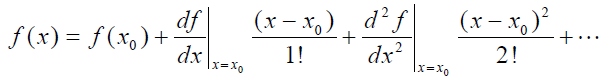
برای تغییرات کوچک $$x$$ حول نقطه $$x_0$$، می‌توانیم از جملات مرتبه بالاتر صرف‌نظر کنیم. در نتیجه، تقریبِ به‌دست آمده، رابطه یک خط راست بین تغییرات $$f(x)$$ و $$x$$ حول نقطه $$x_0$$ است. بنابراین، داریم:

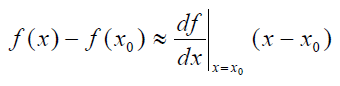
یا

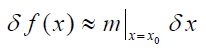
مثال ۲

معادله زیر را حول نقطه $$x=\pi /4$$ خطی کنید.

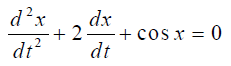
حل: وجود جمله $$\cos (x)$$ سبب غیرخطی شدن معادله شده است. عبارت $$x= \delta x + \pi /4$$ را در نظر بگیرید که در آن، $$\delta x$$ تغییرات کوچکی دارد.

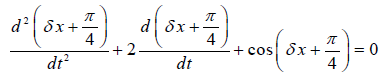
از طرفی، داریم:

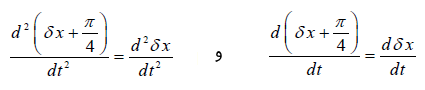
با جایگذاری معادلات بالا در رابطه (۳)، می‌توان نوشت:

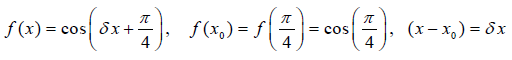
در نتیجه، داریم:

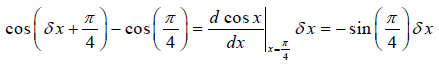
حل معادله بالا، نتیجه می‌دهد:

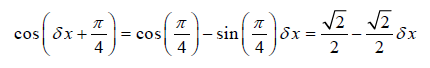
با جایگذاری معادلات (۷) تا (10) در معادله (۶) داریم:

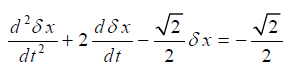
اگر دقت کنیم، می‌بینیم که علی‌رغم همگن بودن معادله غیرخطی (۵)، رابطه خطی‌شده آن، یعنی رابطه (۱۱) غیرهمگن است.

مثال ۳

در مدار غیرخطی شکل زیر، $$v(t)$$ یک منبع ولتاژ متناوب است. رابطه ولتاژ برحسب جریان به‌صورت $$i_r=2e^{0.1v_r}$$ است. تابع تبدیل $$V_L(s)/V(s)$$ را محاسبه کنید.

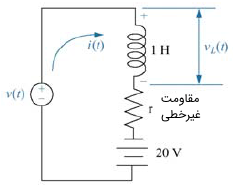
حل: از قانون ولتاژ کیرشهف در حلقه استفاده می‌کنیم و معادله دیفرانسیل غیرخطی را به‌دست می‌آوریم. در نتیجه، داریم:

و

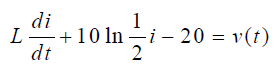
در حالت ماندگار، ولتاژ سلف صفر است و از آن‌جایی که $$V_L(t)=Ldi/dt$$ و $$di/dt$$ نیز در حالت ماندگار صفر است، یک منبع ولتاژ ثابت (باتری) داریم. بنابراین، ولتاژ مقاومت، $$20$$ ولت است. با استفاده از مشخصه مقاومت، جریان $$i_r=i=14.78 \, A$$ به‌دست می‌آید. این جریان، مقدار جریان نقطه تعادل سیستم ($$i_0$$) است. بنابراین:

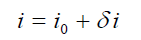
با جایگذاری عبارت بالا در رابطه (۱۲)، خواهیم داشت:

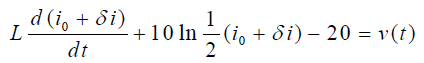
اگر از رابطه (۳) استفاده کنیم، می‌توانیم عبارت $$\text{ln} \frac{1}{2}(i_0+\delta i)$$ را به‌صورت زیر ساده کنیم:

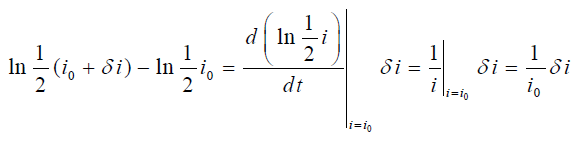
یا

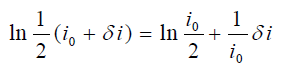
با جایگذاری عبارات بالا در رابطه (۱۳)، معادله خطی به‌صورت زیر به‌دست می‌آید:

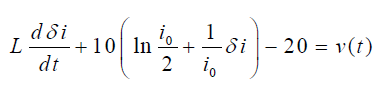
با قرار دادن $$L=1$$ و $$i_0=14.78$$، معادله دیفرانسیل خطی‌شده نهایی به‌صورت زیر خواهد بود:

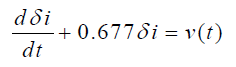
اگر با در نظر گرفتن شرایط اولیه صفر از معادله دیفرانسیل بالا تبدیل لاپلاس بگیریم، داریم:

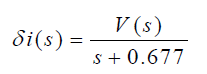
ولتاژ سلف حول نقطه تعادل را نیز می‌توان به‌صورت زیر نوشت:

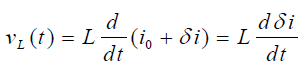
اعمال تبدیل لاپلاس به معادله بالا، نتیجه زیر را خواهد داد:

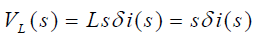
اگر رابطه (۱۸) را در رابطه (۲۰) جایگذاری کنیم، داریم:

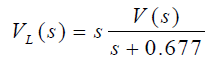
در نهایت، تابع تبدیل مدار حول $$i=14.78$$ یا معادل آن، $$v(t)=0$$ به‌شکل زیر خواهد بود:

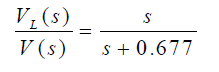
خطی‌سازی معادلات فضای حالت

یکی از مزایای فضای حالت نسبت به تابع تبدیل، توانایی آن در نمایش سیستم‌های غیرخطی است. البته باید توجه داشت که توانایی نمایش سیستم‌های غیرخطی، به‌معنای توانایی در حل معادلات حالت نیست. اگر با تغییرات کوچک حول نقطه تعادل سروکار داشته باشیم، می‌توانیم معادلات حالت را خطی کنیم.

فیلم آموزش کاربرد متلب در کنترل خطی در فرادرس

کلیک کنید

همان‌گونه که قبلاً گفتیم، کلید اصلی خطی‌سازی حول نقطه تعادل، استفاده از سری تیلور است.

برای مثال، سیستم غیرخطی مرتبه‌دوم زیر را در نظر بگیرید:

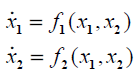
می‌توانیم برای سیستم بالا، سری تیلور را حول نقطه $$(\bar{x_1}, \bar{x_2})$$ به‌صورت زیر بنویسیم:

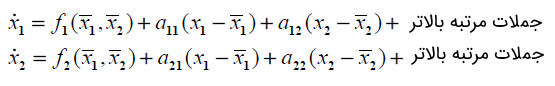
که در آن:

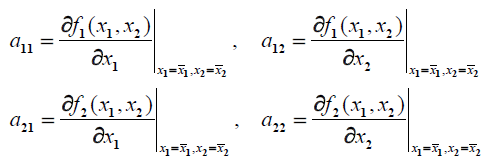
اگر $$(\bar{x_1}, \bar{x_2})$$ یک نقطه تعادل سیستم باشد، داریم:

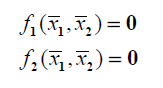
در مثال زیر، معادلات حالت یک پاندول را بیان کرده و نشان می‌دهیم که می‌توان یک سیستم غیرخطی را در فضای حالت نمایش داد. سپس معادلات غیرخطی را حول نقطه تعادل، خطی می‌کنیم.

مثال ۴

پاندول شکل 4 (الف) را در نظر بگیرید. در این شکل، $$Mg$$ وزن، $$T$$ گشتاور اعمالی در جهت $$\theta$$ و $$L$$ طول پاندول است.

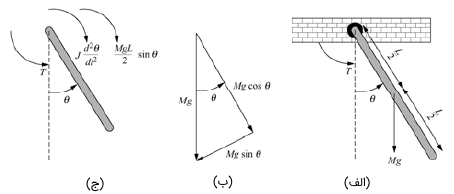
فرض کنید جرم به‌صورت یکنواخت توزیع شده و مرکز جرم در $$L/2$$ قرار دارد. نقطه تعادل در حالتی است که پاندول در وضعیت عمود قرار داشته و سرعت زاویه‌ای آن صفر است. معادله حالت را حول این نقطه، خطی کنید.

حل: ابتدا نمودار جسم آزاد را مطابق شکل 4 (ج) رسم می‌کنیم. معادله گشتاورها به‌صورت زیر است:

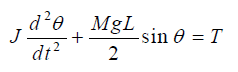
در معادله بالا، $$J$$ ممان اینرسی پاندول حول نقطه چرخش است. متغیرهای حالت جابه‌جایی زاویه‌ای و مشتق آن را به‌عنوان متغیرهای حالت $$x_1$$ و $$x_2$$ در نظر می‌گیریم. در نتیجه، با فرض $$x_1=\theta$$ و $$x_2=d\theta / dt$$ داریم:

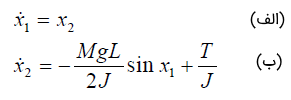
می‌بینیم که معادلات بالا، فضای حالت یک سیستم غیرخطی را نشان می‌دهند. لازم به ذکر است که معادلات (۲۴-الف) و (۲۴-ب) مدل کامل پاندول را در فضای حالت با شرایط اولیه غیرصفر نشان می‌دهند، حتی اگر پارامترهایی مانند جرم و زمان تغییر کنند.

اگر بخواهیم از روش‌های  کلاسیک استفاده و معادلات حالت را به‌صورت تابع تبدیل بیان کنیم، باید آن‌ها را خطی کنیم.

اکنون معادلات را برای نقطه تعادل $$x_1=0$$ و $$x_2=0$$ خطی می‌کنیم. بنابراین، $$x_1$$ و $$x_2$$ حول نقطه تعادل تغییر می‌کنند و آن‌ها را به‌صورت زیر نمایش می‌دهیم:‌

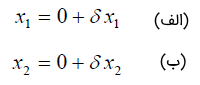
با استفاده از رابطه (۳)، داریم:

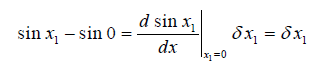
که نتیجه می‌دهد:

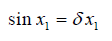
حال خطی‌سازی یک سیستم غیرخطی را در حالت کلی بررسی می‌کنیم.

سیستم فضای حالت (۲۸) را در نظر بگیرید که با معادلات غیرخطی توصیف شده است،

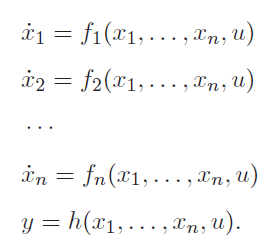
که در آن، $$\text{x}=[x_1, \ldots, x_n]^T$$ بردار حالت سیستم است. اسکالرهای $$u$$ و $$y$$ به‌ترتیب، ورودی کنترل و خروجی سیستم نامیده می‌شوند.

با تعریف:

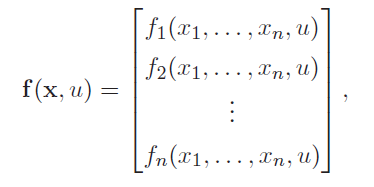
می‌توانیم رابطه (28) را به‌صورت زیر بنویسیم:

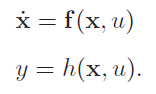
که در آن، $$\mathbf{f}$$ و $$h$$، توابعی غیرخطی از $$\mathrm{x}$$ و $$u$$ هستند.

حال می‌خواهیم معادلات غیرخطی را به‌فرم فضای حالت استاندارد زیر خطی کنیم:

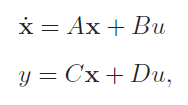
که در آن، $$A$$ یک ماتریس $$n \times n$$، $$B$$ یک بردار $$n\times ۱$$، $$C$$ یک ماتریس سطری $$1 \times n$$ و $$D$$ اسکالر است.

فرض کنید نقطه تعادل سیستم (۲۹)، $$\mathrm{x}^*=[x_1^* \ldots x_n^*]^T$$ با $$u=u^*$$ باشد. عبارت $$\Delta \mathrm{x} = \mathrm{x} - \mathrm {x}^*$$ را تعریف می‌کنیم:

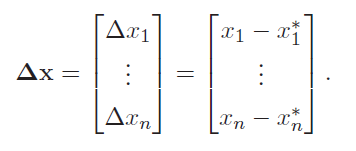
همچنین فرض کنید $$\Delta u=u-u^*$$ و $$\Delta y=y-h(\mathrm{x}^*, u^*)$$. جملات جدید $$\Delta \mathrm{x}$$، $$\Delta u$$ و $$\Delta y$$ به‌ترتیب، تغییرات $$\mathrm{x}$$، $$u$$ و $$y$$ را از نقطه تعادل‌شان نشان می‌دهند. این جملات را به‌عنوان متغیرهای حالت جدید در نظر می‌گیریم.

خطی‌سازی (۲۹) در $$\mathrm{x}^*$$ به معادلات زیر می‌انجامد:

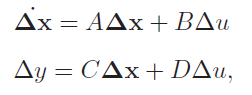
که در آن:

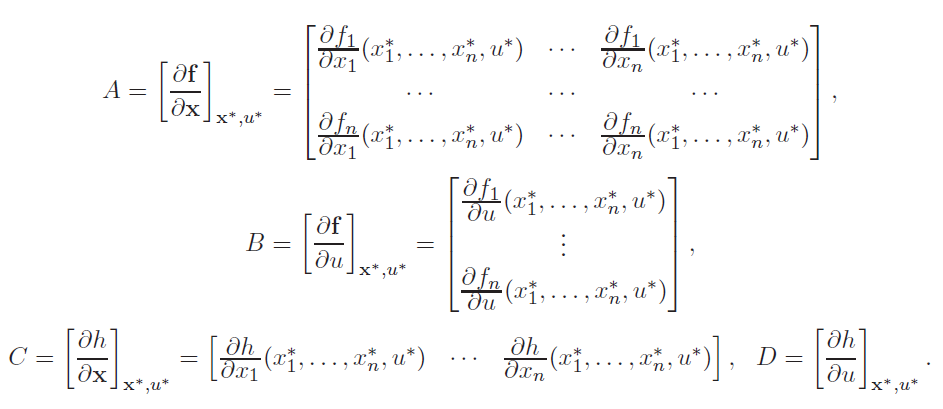
رابطه (۳۱)، مدل سیگنال‌کوچک نامیده می‌شود و فقط در همسایگی کوچکی از نقطه تعادل $$\mathrm{x}^*$$ معتبر است. ماتریس‌های $$\frac{\partial \mathbf{f}}{\partial u}$$، $$\frac{\partial \mathbf{f}}{\partial \mathrm{x}}$$، $$\frac{\partial h}{\partial \mathrm{x}}$$ و $$\frac{\partial h}{\partial u}$$ ماتریس ژاکوبی نام دارند و آن را با $$J$$ نشان می‌دهند.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• نمایش سیستم های دینامیکی با متلب — از صفر تا صد
• فیدبک (Feedback) در سیستم های کنترل — مفاهیم اصلی

^^