دستگاه معادلات دیفرانسیل خطی با ضرایب متغیر — از صفر تا صد

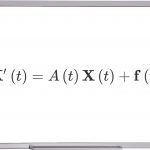
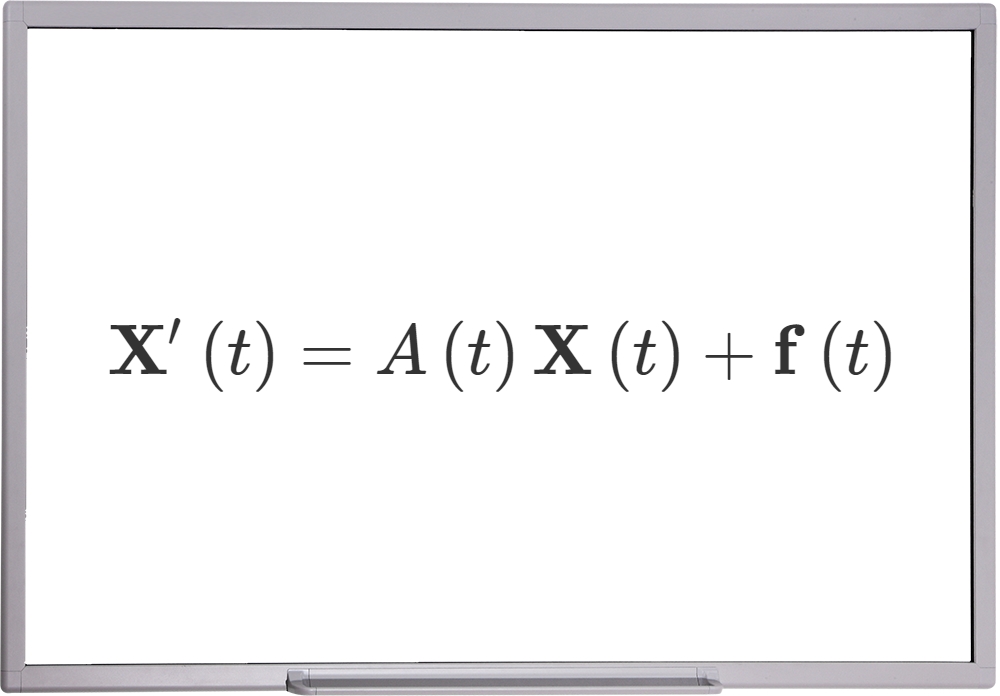
در مطالب قبلی از مجموعه آموزش‌های ریاضیات مجله فرادرس، درباره دستگاه معادلات دیفرانسیل خطی با ضرایب ثابت بحث کردیم. در این آموزش، روش حل دستگاه معادلات دیفرانسیل خطی با ضرایب متغیر را بررسی می‌کنیم.

دستگاه معادلات دیفرانسیل خطی با ضرایب متغیر

یک دستگاه معادلات دیفرانسیل معمولی با ضرایب متغیر، به‌صورت زیر نوشته می‌شود:

$$\large { \frac { { d { x _ i }  } } { { d t } } = { x ’ _ i } } = { \sum \limits_{ j = 1 } ^ n { { a _ { i j } } \left( t \right) { x _ j } \left( t \right)} + { f _ i }\left( t \right),\;\;}\kern-0.3pt { i = 1,2, \ldots ,n,}$$

که در آن، $${{x_i}\left( t \right)}$$ توابع مجهولی هستند که در بازه $$\left[ { a , b } \right]$$ پیوسته و مشتق‌پذیرند. ضرایب $${{a_{ij}}\left( t \right)}$$ و جملات آزاد $${f_i}\left( t \right)$$، توابعی پیوسته در بازه $$\left[ { a , b } \right]$$ هستند.

دستگاه معادلات را به‌صورت ماتریسی-برداری زیر می‌نویسیم:

$$\large { { \mathbf{X}}\left( t \right) } = { A \left( t \right) { \mathbf{X}}\left( t \right) + { \mathbf{f}} \left( t \right),}$$

که در آن:

$$ \large { { \mathbf{X} } \left( t \right) = \left[ { \begin{array}{*{20}{c}}<br /> { { x _ 1 } \left( t \right)}\\<br /> { { x _ 2 } \left( t \right)}\\<br /> \vdots \\<br /> { { x _ n }\left( t \right)}<br /> \end{array}} \right],\;\;}\kern-0.3pt<br /> { { A \left( t \right) \text{ = }}\kern0pt{\left[ {\begin{array}{*{20}{c}}<br /> { { a _ { 1 1 } } \left( t \right)}&{ { a _ {  1 2 } } \left( t \right)}& \vdots &{{a_{1n}}\left( t \right)}\\<br /> { { a _ { 2 1 } } \left( t \right)}& { { a _{ 2 2  } } \left( t \right)}& \vdots & { { a  _ { 2 n } } \left( t \right) }\\<br /> \cdots & \cdots & \cdots & \cdots \\<br /> { {  a _ {  n 1 } } \left( t \right)}&{ { a _ { n 2 } } \left( t \right) }& \vdots & { { a _ { n n } } \left( t \right)}<br /> \end{array}} \right],\;\;}}\kern-0.3pt<br /> { { \mathbf{f}}\left( t \right) = \left[ {\begin{array}{* { 2 0 } { c } }<br /> { { f _ 1 }\left( t \right)}\\<br /> { { f _ 2 }\left( t \right)}\\<br /> \vdots \\<br /> { { f _ n } \left( t \right)}<br /> \end{array}} \right].} $$

در حالت کلی، ماتریس $$A\left( t \right)$$ و بردار توابع $${\mathbf{X}}\left( t \right)$$ و $${\mathbf{f}}\left( t \right)$$ دارای هر دو مقدار حقیقی و مختلط هستند.

دستگاه همگن متناظر با ضرایب متغیر به‌فرم برداری زیر است:

$$\large { \mathbf{ X ’ } } \left( t \right) = A \left( t \right) { \mathbf{ X }}\left( t \right).$$

دستگاه اساسی جواب‌ها و ماتریس اساسی

توابع برداری $${\mathbf{x}_1}\left( t \right)$$، $${\mathbf{x}_2}\left( t \right)$$، $$\cdots$$ و $${\mathbf{x}_n}\left( t \right)$$ در بازه $$\left[ {a,b} \right]$$ وابسته خطی هستند، اگر اعداد $$c_1$$، $$c_2$$، $$\cdots$$ و $$c_n$$ همگی صفر نباشند و رابطه زیر برقرار باشد:

$$\large { { c _ 1  }{ \mathbf{ x } _ 1 }\left( t \right) + { c _ 2  } { \mathbf{ x } _ 2 }\left( t \right) + \cdots }+{ { c _ n }{ \mathbf{ x } _ n }\left( t \right) \equiv 0,\;\;}\kern-0.3pt {\forall t \in \left[ {a,b} \right].}$$

اگر این معادله فقط در شرایطِ

$$\large {{c_1} = {c_2} = \cdots }={ {c_n} = 0,}$$

برقرار باشد، توابع برداری $${\mathbf{x}_i}\left( t \right)$$، در بازه داده‌شده مستقل خطی نامیده می‌شوند.

هر دستگاه با $$n$$ جواب مستقل خطی $${\mathbf{x}_1}\left( t \right)$$، $${\mathbf{x}_۲}\left( t \right)$$، $$\cdots$$ و $${\mathbf{x}_n}\left( t \right)$$ یک دستگاه اساسی یا پایه از جواب‌ها نامیده می‌شود.

ماتریس مربعی $$\Phi\left( t \right)$$ که ستون‌های آن از جواب‌های مستقل خطی $${\mathbf{ x } _ 1}\left( t \right)$$، $${\mathbf{ x } _ ۲}\left( t \right)$$، $$\cdots$$ و $${\mathbf{ x } _ n}\left( t \right)$$ تشکیل شده‌، ماتریس اساسی دستگاه معادلات نامیده می‌شود و به‌فرم زیر است:

$$ \large \require{cancel}<br /> \mathbf{ X ’ }\left( t \right) = A \left( t \right)\mathbf{X}\left( t \right) + \mathbf{f}\left( t \right),\;\;\Rightarrow<br /> {\cancel{ \Phi ’ \left( t \right)\mathbf{C}\left( t \right)} + \Phi \left( t \right)\mathbf{C’}\left( t \right) } \\ \large<br /> = {\cancel{A\left( t \right)\Phi \left( t \right)\mathbf{C}\left( t \right)} + \mathbf{ f } \left( t \right),\;\;}\Rightarrow<br /> {\Phi \left( t \right)\mathbf{C’}\left( t \right) = \mathbf{f}\left( t \right).} $$

که در آن، $${{x_{ij}}\left( t \right)}$$ مؤلفه‌های بردار جواب‌های مستقل خطی $${\mathbf{x}_1}\left( t \right)$$، $${\mathbf{x}_۲}\left( t \right)$$، $$\cdots$$ و $${\mathbf{x}_n}\left( t \right)$$ هستند.

لازم به ذکر است که ماتریس اساسی $$\Phi \left( t \right)$$ غیرمنفرد است، یعنی ماتریس معکوس $${\Phi ^{ – 1}}\left( t \right)$$ وجود دارد. از آنجایی که ماتریس اساسی، $$n$$ جواب مستقل خطی دارد، از جایگذاری آن در دستگاه همگن، رابطه زیر به‌دست می‌آید:

$$\large \Phi’\left( t \right) \equiv A\left( t \right)\Phi \left( t \right) .$$

معادله اخیر را از سمت راست، در ماتریس معکوس $${\Phi ^{ – 1}}\left( t \right)$$ ضرب می‌کنیم:

$$\large { { \Phi’\left( t \right) { \Phi ^ { – 1 } }\left( t \right) }\equiv{ A\left( t \right)\Phi \left( t \right) { \Phi^{ – 1 } } \left( t \right),\;\; } } \Rightarrow { A \left( t \right) \equiv \Phi’\left( t \right) { \Phi ^ { – 1 } } \left( t \right) . }$$

رابطه منتجه، به‌طور منحصربه‌فرد، یک دستگاه معادلات همگن را ارائه می‌کند که ماتریس اساسی را نتیجه می‌دهد.

جواب عمومی دستگاه همگن برحسب ماتریس اساسی، به‌صورت زیر است:

$$\large {\mathbf{ X } _ 0 }\left( t \right) = \Phi \left( t \right)\mathbf{ C }$$

که در آن، $$\mathbf{C}$$ یک بردار $$n$$بُعدی شامل اعداد دلخواه است.

در اینجا، حالت خاص دستگاه‌ معادلات همگن را بررسی می‌کنیم. اگر ضرب ماتریس $$A\left( t \right)$$ در انتگرال این ماتریس، جابه‌جایی‌پذیر باشد، یعنی:

$$\large { A \left( t \right) \cdot \int\limits_a^t { A \left( \tau \right) d t } } = { \int\limits_a^t { A\left( \tau \right)dt} \cdot A\left( t \right),}$$

ماتریس اساسی $$\Phi\left( t \right)$$ این دستگاه معادلات، با رابطه زیر بیان می‌شود:

$$\large \Phi \left( t \right) = { e ^ { \,\int\limits_a^t {A\left( \tau \right)d\tau } } } .$$

این ویژگی، در ماتریس‌های متقارن و به‌طور خاص در ماتریس‌های قطری برقرار است.

فرمول رونسکین و لیوویل

دترمینان ماتریس اساسی $$\Phi\left( t \right)$$، «رونسکین» (Wronskian) دستگاه جواب‌های $${\mathbf{x}_1}\left( t \right)$$، $${\mathbf{x}_۲}\left( t \right)$$، $$\cdots$$ و $${\mathbf{x}_n}\left( t \right)$$ نامیده می‌شود:

$$ \large {W\left( t \right) }={ W\left[ {{\mathbf{x}_1},{\mathbf{x}_2}, \ldots ,{\mathbf{x}_n}} \right] \text{ = }}\kern0pt<br /> {\left| {\begin{array}{*{20}{c}}<br /> {{x_{11}}\left( t \right)}&{{x_{12}}\left( t \right)}& \vdots &{{x_{1n}}\left( t \right)}\\<br /> {{x_{21}}\left( t \right)}&{{x_{22}}\left( t \right)}& \vdots &{{x_{2n}}\left( t \right)}\\<br /> \cdots & \cdots & \cdots & \cdots \\<br /> {{x_{n1}}\left( t \right)}&{{x_{n2}}\left( t \right)}& \vdots &{{x_{nn}}\left( t \right)}<br /> \end{array}} \right|.} $$

رونسکین، برای بررسی استقلال خطی جواب‌ها مفید است. با استفاده از رونسکین می‌توان موارد زیر را بیان کرد:

• جواب‌های $${\mathbf{x}_1}\left( t \right)$$، $${\mathbf{x}_۲}\left( t \right)$$، $$\cdots$$ و $${\mathbf{x}_n}\left( t \right)$$ دستگاه همگن، یک دستگاه اساسی تشکیل می‌دهند اگر و فقط اگر رونسکین متناظر، در هیچ نقطه‌ای از بازه $$\left[ {a,b} \right]$$ صفر نباشد.
• جواب‌های $${\mathbf{x}_1}\left( t \right)$$، $${\mathbf{x}_۲}\left( t \right)$$، $$\cdots$$ و $${\mathbf{x}_n}\left( t \right)$$ در بازه $$\left[ {a,b} \right]$$ وابسته خطی هستند اگر و فقط اگر رونسکین در این بازه به‌صورت تحلیلی صفر باشد.

رونسکین جواب‌های $${\mathbf{x}_1}\left( t \right)$$، $${\mathbf{x}_۲}\left( t \right)$$، $$\cdots$$ و $${\mathbf{x}_n}\left( t \right)$$ با «فرمول لیوویل» (Liouville’s Formula) محاسبه می‌شود:

$$\large W\left( t \right) = {e^{\,\int\limits_a^t {\text{tr}\left( {A\left( \tau \right)} \right)d\tau } }},$$

که در آن، $${\text{tr}\left( {A\left( \tau \right)} \right)}$$ اثر ماتریس $${A\left( \tau \right)}$$ (یعنی مجموع درایه‌های قطر اصلی) است:

$$\large {\text{tr}\left( {A\left( \tau \right)} \right) }={ {a_{11}}\left( \tau \right) + {a_{22}}\left( \tau \right) + \cdots }+{ {a_{nn}}\left( \tau \right).}$$

در حالتی که جواب خصوصی معلوم باشد، می‌توان از فرمول لیوویل برای تشکیل جواب عمومی دستگاه همگن استفاده کرد.

روش تغییر ثابت‌ها (روش لاگرانژ)

اکنون درباره دستگاه‌های ناهمگن بحث می‌کنیم که می‌توان آن‌ها را به‌فرم برداری-ماتریسی زیر نوشت:

$$\large {\mathbf{X’}\left( t \right) }={ A\left( t \right)\mathbf{X}\left( t \right) + \mathbf{f}\left( t \right).}$$

جواب عمومی چنین دستگاهی، مجموع جواب عمومی $${\mathbf{X}_0}\left( t \right)$$ دستگاه همگن متناظر و یک جواب خصوصی $${\mathbf{X}_1}\left( t \right)$$ دستگاه ناهمگن است. یعنی:

$$\large {\mathbf{X}\left( t \right) }={ {\mathbf{X}_0}\left( t \right) + {\mathbf{X}_1}\left( t \right) } = {\Phi \left( t \right)\mathbf{C} + {\mathbf{X}_1}\left( t \right),}$$

که در آن، $$\Phi \left( t \right)$$ یک ماتریس اساسی و $$\mathbf{C}$$ یک بردار دلخواه است.

متداول‌ترین روش برای حل دستگاه‌های ناهمگن، روش تغییر ثابت‌ها (روش لاگرانژ) است. در این روش، به‌جای بردار ثابت $$\mathbf{C}$$، بردار $$\mathbf{C}\left( t \right)$$ در نظر گرفته می‌شود که مؤلفه‌های آن، توابع پیوسته مشتق‌پذیری از متغیر مستقل $$t$$ هستند، یعنی فرض می‌کنیم:

$$\large \mathbf{X}\left( t \right) = \Phi \left( t \right)\mathbf{C}\left( t \right).$$

با جایگذاری رابطه اخیر در دستگاه ناهمگن، بردار مجهول $$\mathbf{C}\left( t \right)$$ به‌دست می‌آید:

$$ \large \require{cancel}<br /> {\mathbf{X’}\left( t \right) = A\left( t \right)\mathbf{X}\left( t \right) + \mathbf{f}\left( t \right),\;\;}\Rightarrow<br /> {\cancel{\Phi’\left( t \right)\mathbf{C}\left( t \right)} + \Phi \left( t \right)\mathbf{C’}\left( t \right) } \\ \large<br /> = {\cancel{A\left( t \right)\Phi \left( t \right)\mathbf{C}\left( t \right)} + \mathbf{f}\left( t \right),\;\;}\Rightarrow<br /> {\Phi \left( t \right)\mathbf{C’}\left( t \right) = \mathbf{f}\left( t \right).} $$

از آنجایی که ماتریس $$\Phi \left( t \right)$$ نامنفرد است، معادله اخیر را از چپ در $${\Phi^{ – 1}}\left( t \right)$$ ضرب می‌کنیم:

$$\large {{{\Phi^{ – 1}}\left( t \right)\Phi \left( t \right)\mathbf{C’}\left( t \right) }={ {\Phi^{ – 1}}\left( t \right)\mathbf{f}\left( t \right),\;\;}} \\ \large \Rightarrow {\mathbf{C’}\left( t \right) = {\Phi^{ – 1}}\left( t \right)\mathbf{f}\left( t \right).}$$

بعد از انتگرال‌گیری، ماتریس $$\mathbf{C}\left( t \right)$$ به‌دست می‌آید.

مثال‌ها

در ادامه، چند مثال را بررسی می‌کنیم.

مثال ۱

دستگاه خطی معادلاتی با جواب‌های زیر را بنویسید:

$$ \large { { \mathbf{ x } _ 1 }\left( t \right) = \left[ {\begin{array}{*{ 2 0 } { c } }<br /> 2\\<br /> t<br /> \end{array}} \right],\;\;}\kern-0.3pt<br /> {{\mathbf{ x } _ 2 }\left( t \right) = \left[ {\begin{array}{*{ 2 0 } { c } }<br /> t\\<br /> { { t ^ 2  } }<br /> \end{array}} \right],\;\;}\kern-0.3pt<br /> {t \ne 0.} $$

حل: در این مسئله، ماتریس اساسی دستگاه به‌صورت زیر است:

$$ \large \Phi \left( t \right) = \left[ {\begin{array}{ * { 2 0 } { c } }<br /> 2&t\\<br /> t&{ { t ^ 2 } }<br /> \end{array}} \right]. $$

اکنون ماتریس معکوس $${\Phi ^{ – 1}}\left( t \right)$$ را محاسبه می‌کنیم:

$$ \large { { \Delta \left( \Phi \right) = \left|  { \begin{array}{* { 2 0 } { c } }<br /> 2&t\\<br /> t& { {  t ^ 2 } }<br /> \end{array}} \right| }={ 2{t^2} – {t^2} = {t^2},\;\;}}\\ \large \Rightarrow<br /> {{\Phi ^ { – 1 } } \left( t \right) = \frac{ 1 }{ { \Delta \left( \Phi \right) } } C _ { i j } ^ T }<br /> = {\frac{ 1 }{ { { t ^ 2 }  } } { \left[ {\begin{array} { * { 2 0 } { c } }<br /> { {t ^ 2 } } &{ – t}\\<br /> { – t }&2<br /> \end{array}} \right]^T} }\\ \large<br /> = {\frac{1}{ { {t ^ 2 }  } } \left[ {\begin{array}{ * { 2 0 } { c } }<br /> { { t ^ 2 } } & { – t } \\<br /> { – t } & 2<br /> \end{array}} \right] }<br /> = {\left[ {\begin{array}{*{20}{c}}<br /> 1&{ – \frac{1}{t}}\\<br /> { – \frac{ 1 } { t } } &{\frac{2}{ { { t  ^ 2  } } } }<br /> \end{array}} \right].} $$

در معادلات بالا، $${C_{ij}}$$ همسازه‌های متناظر با درایه‌های ماتریس اساسی $$\Phi \left( t \right)$$ هستند.

ماتریس ضرایب دستگاه معادلات به‌صورت زیر است:

$$\large A\left( t \right) = \Phi’\left( t \right) { \Phi ^ { – 1 } } \left( t \right).$$

مشتق ماتریس اساسی برابر است با (درایه به درایه حساب می‌شود):

$$ \large { \Phi ’ } \left( t \right) = \left[ {\begin{array} { * { 2 0 } { c } }<br /> 0&1\\<br /> 1& { { 2 t } }<br /> \end{array}} \right]. $$

بنابراین، داریم:

$$ \large {A\left( t \right) }={ \left[ {\begin{array} { * { 2 0 } { c } }<br /> 0&1\\<br /> 1& { 2 t }<br /> \end{array}} \right]\left[ {\begin{array} { * { 2 0 } { c } }<br /> 1 & { – \frac{ 1 } { t }  } \\<br /> { – \frac{1}{t } } & {\frac{2} { { { t ^ 2 } } } }<br /> \end{array}} \right] } \\ \large<br /> = {\left[ {\begin{array}{*{20}{c}}<br /> {0 – \frac{1}{t}}&{0 + \frac{2}{{{t^2}}}}\\<br /> {1 – 2}&{ – \frac{ 1 } { t } + \frac{ 4 } { t } }<br /> \end{array}} \right] }<br /> = {\left[ {\begin{array}{ * {  2 0 } { c } }<br /> { – \frac{ 1 } { t }  } & { \frac{ 2 } { { { t ^ 2 } } } } \\<br /> { – 1 }&{\frac{ 3 } { t } }<br /> \end{array}} \right].} $$

در نتیجه، دستگاه معادلات که جواب‌های آن، $${\mathbf{x}_1}\left( t \right)$$ و $${\mathbf{x}_2}\left( t \right)$$ است، به‌صورت زیر خواهد بود:

$$\large {\frac{ { d x }  } { { d t } } = – \frac{ x } { t } + \frac { { 2 y }  } { {  { t ^ 2 } } } ,\;\;}\kern-0.3pt {\frac{ { d y } } { { d t } } = – x + \frac{ { 3 y }} { t }  . }$$

مثال ۲

جواب عمومی دستگاه معادلاتِ

$$\large {\frac{ {dx}}{{dt}} = – tx + y,\;\;}\kern-0.3pt {\frac{{dy}}{{dt}} = \left( {1 – { t ^ 2 } } \right)x + ty,\;\;}\kern-0.3pt {x \gt 0}$$

را با دانستن جواب زیر بیابید:

$$ \large { \mathbf{ X } _ 1 }\left( t \right) = \left[ {\begin{array}{ * { 2 0 } { c } }<br /> { { x _ 1  } \left( t \right)}\\<br /> { { y _  1 } \left( t \right) }<br /> \end{array}} \right] = \left[ {\begin{array}{ * { 2 0 } { c } }<br /> 1\\<br /> t<br /> \end{array}} \right]. $$

حل: جواب مستقل خطی دوم را با تابع برداری زیر نمایش می‌دهیم:

$$ \large { \mathbf{ X } _ 2 } \left( t \right) = \left[ {\begin{array}{ * { 2 0 } { c } }<br /> { { x _ 2 } \left( t \right)}\\<br /> { { y _ 2 }\left( t \right)}<br /> \end{array}} \right] = \left[ {\begin{array}{ * { 2 0 }  { c } }<br /> u\\<br /> v<br /> \end{array}} \right] $$

که شرایط اولیه، $$u\left( {t = 0} \right) = 0$$ و $$v\left( {t = 0} \right) = 1$$ است.

می‌توانیم از فرمول لیوویل استفاده کنیم:

$$ \large {W\left( t \right) = \left| {\begin{array}{*{20}{c}}<br /> 1&u\\<br /> t&v<br /> \end{array}} \right| }<br /> = {\left| {\begin{array}{*{20}{c}}<br /> 1&0\\<br /> t&1<br /> \end{array}} \right|{e^{\,\int\limits_0^t {\left( {A\left( \tau \right)} \right)d\tau } }} } \\ \large<br /> = {1 \cdot {e^{\,\int\limits_0^t {\left( { – \tau + \tau } \right)d\tau } }} }<br /> = {{e^{\,\int\limits_0^t {0d\tau } }} }<br /> = {{e^0} = 1.} $$

در نتیجه، رابطه بین توابع مجهول $$u$$ و $$v$$ به‌دست می‌آید:

$$\large v – tu = 1.$$

معادله دوم دستگاه اصلی را در نظر بگیرید. با جایگذاری جواب $${\mathbf{X}_2}\left( t \right)$$، داریم:

$$\large {\frac{{dv}}{{dt}} }={ \left( {1 – {t^2}} \right)u + tv.}$$

از معادله قبل جمله $$tv$$ را می‌توان به‌صورت زیر نوشت:

$$\large {v – tu = 1,\;\; }\Rightarrow {tv – {t^2}u = t,\;\;}\Rightarrow {tv = {t^2}u + t.}$$

با جایگذاری معادله اخیر در معادله دیفرانسیل تابع $$v(t)$$، داریم:

$$ \large \require{cancel}<br /> {\frac{{dv}}{{dt}} = \left( {1 – {t^2}} \right)u + tv,\;\;}\Rightarrow<br /> {\frac{{dv}}{{dt}} = \left( {1 – {t^2}} \right)u + {t^2}u + t,\;\;} \\ \large\Rightarrow<br /> {\frac{{dv}}{{dt}} = u – \cancel{{t^2}u} + \cancel{{t^2}u} + t,\;\;}\Rightarrow<br /> {\frac{{dv}}{{dt}} = u + t,\;\;}\Rightarrow<br /> {t\frac{{dv}}{{dt}} = tu + {t^2}.} $$

با توجه به اینکه $$tu = v – 1$$، یک معادله دیفرانسیل مرتبه اول برای تابع $$v(t)$$ به‌دست می‌آید:

$$\large t\frac{{dv}}{{dt}} = v – 1 + {t^2}$$

یا

$$\large {t\frac{{dv}}{{dt}} = v + {t^2} – 1.}$$

ابتدا جواب متناظر با معادله همگن را پیدا می‌کنیم:

$$\large {t\frac{{dv}}{{dt}} = v,\;\; }\Rightarrow {\frac{{dv}}{v} = \frac{{dt}}{t},\;\;}\Rightarrow {\int {\frac{{dv}}{v}} = \int {\frac{{dt}}{t}} ,\;\;} \\ \large\Rightarrow {\ln \left| v \right| = \ln \left| t \right| + \ln C,\;\;}\Rightarrow {{v_0}\left( t \right) = Ct,}$$

که در آن، $$C$$ یک عدد دلخواه است.

اکنون، جواب معادله ناهمگن را با استفاده از روش تغییر پارامتر تعیین می‌کنیم:

$$\large {v\left( t \right) = C\left( t \right)t,\;\;}\Rightarrow {\frac{{dv\left( t \right)}}{{dt}} }={ \frac{{dC\left( t \right)}}{{dt}}t + C\left( t \right).}$$

بعد از جایگذاری، توصیف مشتق $${\large\frac{{dC}}{{dt}}\normalsize}$$ را به‌دست می‌آوریم:

$$\large {{t\left( {t\frac{{dC}}{{dt}} + C} \right) }={ Ct + {t^2} – 1,\;\;}}\\ \large \Rightarrow {{{t^2}\frac{{dC}}{{dt}} + \cancel{Ct} }={ \cancel{Ct} + {t^2} – 1,\;\;}}\Rightarrow {{\frac{{dC}}{{dt}} = \frac{{{t^2} – 1}}{{{t^2}}} }={ 1 – \frac{1}{{{t^2}}}.}}$$

با انتگرال‌گیری از معادله فوق، مقدار $$C\left( t \right)$$ به‌دست می‌آید:

$$\large {C\left( t \right) }={ \int {\left( {1 – \frac{1}{{{t^2}}}} \right)dt} }={ t + \frac{1}{t}.}$$

تابع $$v\left( t \right)$$ با فرمول زیر بیان می‌شود:

$$\large {v\left( t \right) = C\left( t \right)t }={ {t^2} + 1.}$$

اکنون یافتن تابع $$u(t)$$ ساده است:

$$\large {v – tu = 1,\;\; }\Rightarrow {tu = v – 1,\;\;} \\ \large \Rightarrow {tu = {t^2} + \cancel{1} – \cancel{1},\;\;} {\Rightarrow u\left( t \right) = t.}$$

بنابراین، جواب دوم دستگاه به‌صورت زیر است:‌

$$ \large {{\mathbf{X}_2}\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br /> {{x_2}\left( t \right)}\\<br /> {{y_2}\left( t \right)}<br /> \end{array}} \right] }<br /> = {\left[ {\begin{array}{*{20}{c}}<br /> u\\<br /> v<br /> \end{array}} \right] }<br /> = {\left[ {\begin{array}{*{20}{c}}<br /> t\\<br /> {{t^2} + 1}<br /> \end{array}} \right].} $$

جواب کلی را نیز می‌توان به‌صورت زیر نوشت:

$$ \large {\mathbf{X}\left( t \right) }={ {C_1}{\mathbf{X}_1}\left( t \right) + {C_2}{\mathbf{X}_2}\left( t \right) }<br /> = {{{C_1}\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> t<br /> \end{array}} \right] }+{ {C_2}\left[ {\begin{array}{*{20}{c}}<br /> t\\<br /> {{t^2} + 1}<br /> \end{array}} \right],}} $$

که در آن، $$C_1$$ و $$C_2$$ ثابت‌هایی دلخواه هستند.