راهنمای محاسبه با اعداد مختلط – به زبان ساده
اعداد موهومی یک توضیح شهودی دارند. آنها باعث ایجاد چرخش در اعداد میشوند، همان طور که اعداد منفی باعث میشوند، یک بازتاب از عدد داشته باشیم. این بینش باعث میشود که درک محاسبه با اعداد مختلط آسانتر شود و روشی عالی برای بررسی مجدد نتایج محسوب میشود. راهنمای سریع آن چنین است:
| ردیف | عملیات مختلط | معنای شهودی |
|---|---|---|
| 1 | بزرگی |z| | فاصله از صفر |
| 2 | جمع و تفریق | لغزش اعداد |
| 3 | ضرب | مقیاسبندی با استفاده از بزرگی و زاویه |
| 4 | تقسیم | کاهش بزرگی و کسر زاویه |
| 5 | مزدوج مختلط *z | «بازتاب موهومی»: همان اندازه، زاویه مقابل. اگر z=3+4i در این صورت z*=3-4i |
| 6 | مشخصات مزدوج | جمع و سپس بازتاب = بازتاب و سپس جمع |
در این مقاله به بررسی معانی شهودی میپردازیم.
متغیرهای مختلط
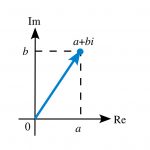
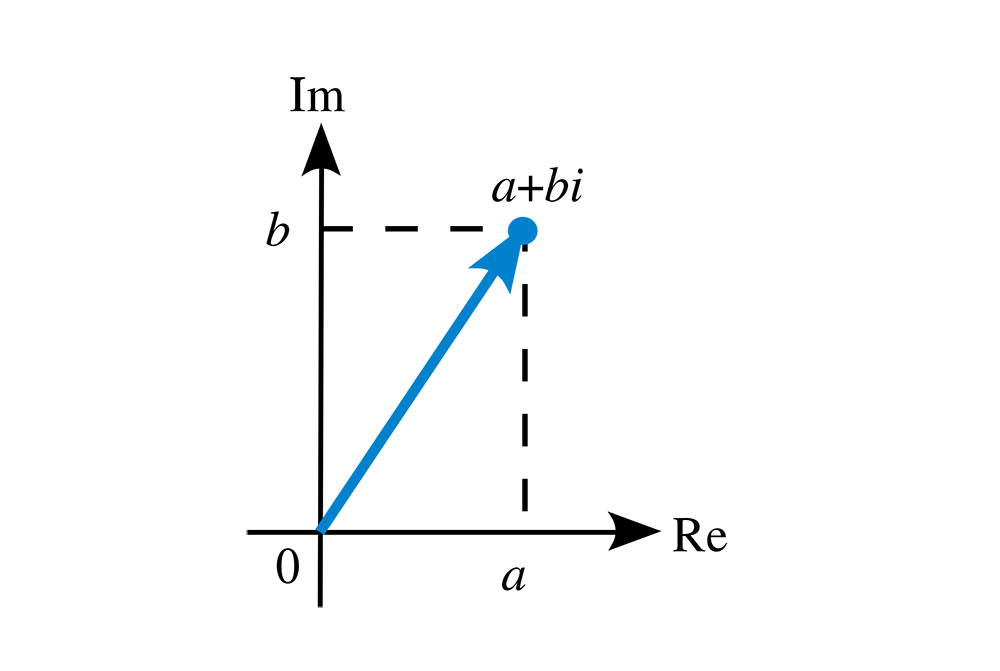
در جبر معمولی غالباً از تساویهایی مانند x=3 استفاده میکنیم و معنای آن کاملاً واضح است، یعنی عددی مانند x هست که مقدار آن 3 است. در اعداد مختلط یک مشکل وجود دارد، چون ما در مورد دو بُعد صحبت میکنیم. یعنی وقتی مینویسیم:
Z = 3 + 4i
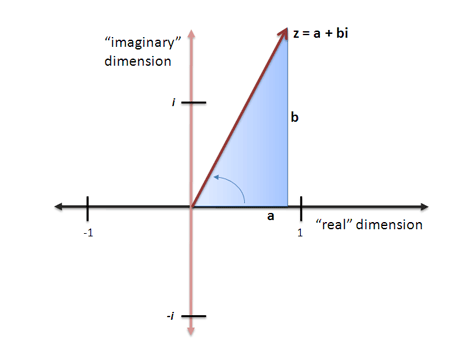
میگوییم عدد z وجود دارد که دو بخش دارد: 3 (بخش حقیقی) و 4i (بخش موهومی). البته این که چگونه یک عدد میتواند دو بخش داشته باشید تا حدودی عجیب به نظر میرسد؛ اما ما قبلاً نیز با این طرز بیان آشنا شدهایم و غالباً مینویسیم:
و ناراحت هم نمیشویم که عدد منفرد y هم بخش صحیح (3) و هم بخش کسری () دارد. Y ترکیبی از این دو بخش است. اعداد مختلط نیز مشابه هستند. آنها هم بخش حقیقی (به اختصار RE) و هم بخش موهومی (به اختصار Im) دارند که در یک متغیر واحد جای گرفتهاند.
متأسفانه ما هنوز نمادگذاری زیبایی مانند 3.4 برای ادغام بخشهای حقیقی و موهومی در یک عدد منفرد نداریم. شاید بهتر باشد بخش موهومی به صورت عمودی به صورت کمرنگ نوشته شود؛ اما این ایده چندان متداول نیست، پس همچنان از قالب «a + bi» استفاده میکنیم.
اندازهگیری
از آنجا که اعداد مختلط از دو محور مستقل از هم استفاده میکنند، اندازه (بزرگی) آنها را میتوانیم با استفاده از قضیه فیثاغورس بیابیم:
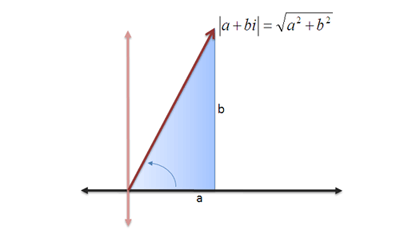
بنابراین عدد z=3+4i باید بزرگی برابر با 5 داشته باشد. علامت اختصاری برای بزرگی z به صورت |z| است. این علامت کاملاً شبیه علامت قدر مطلق است، چون بزرگی عدد مختلط فاصله آن از صفر را اندازهگیری میکند، همان طور که قدر مطلق نیز فاصله عدد از صفر را اندازه میگیرد.
جمع و تفریق مختلط
در مطالب قبلی وبلاگ فرادرس در مورد اعداد مختلط دیدیم که جمع معمولی اعداد را میتوان مانند لغزاندن اعداد تصور کرد.
جمع اعداد مختلط نیز مشابه است؛ اما میتوانیم این لغزش را در دو بعد (حقیقی و موهومی) داشته باشیم. برای نمونه:
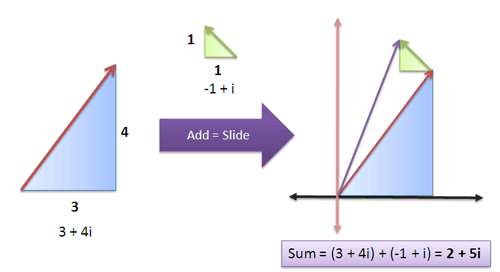
جمع با نتیجهای برابر با دارد.
در این مورد نیز یک بازنمایی بصری در مورد چگونگی ترکیب «مؤلفههای مستقل» وجود دارد و باید بخشهای حقیقی و موهومی را به صورت مجزا ردگیری کنیم.
تفریق حالت معکوس جمع است، یعنی لغزش در مسیر معکوس صورت میگیرد. تفریق همان جمع یا جمع است.
ضرب مختلط
این همان جایی است که ریاضیات جالب میشود. وقتی دو عدد مختلط مانند x و y را برای رسیدن به z در هم ضرب میکنیم:
- زاویهها با هم جمع میشوند یعنی زاویه (z) = زاویه (x) + زاویه (y)
- بزرگیها در هم ضرب میشود: |z| = |x| × |y|
یعنی زاویه z مجموع زوایای x+y است و بزرگی z حاصلضرب بزرگیها است. باور کنید یا نه، در هر صورت این رابطه عجیب در مورد ضرب اعداد مختلط برقرار است.
ضرب کردن در یک بزرگی (اندازه) معنی دارد و ما این کار را در مورد اعداد معمولی انجام میدهیم. ضرب 3 × 4 یعنی 3 را در اندازه 4 ضرب کنیم. دلیل این که جمعکردن زاویهها صحیح است نیاز به توضیح بیشتری دارد و آن را به مطلب دیگری موکول میکنیم. اینک نوبت یک مثال رسیده است. فرض کنید میخواهیم z = 3 + 4i را در خودش ضرب کنیم. پیش از آن که به اعمال ریاضی بپردازیم باید چند نکته را بدانیم:
- بزرگی حاصل برابر با 25 خواهد بود، چون z بزرگی برابر با 5 دارد و از این رو z| × |z| = 25|.
- زاویه حاصل بالاتر از 90 خواهد بود، زیرا بالاتر از 45 درجه است (چون برابر با 45 درجه است) و از این رو زاویه نهایی بیش از 90 درجه خواهد بود.
بر اساس پیشبینی روی کاغذ میتوانیم محاسبات زیر را انجام دهیم:
زمان بررسی نتایج رسیده است:
- بزرگی: که با حدس ما برابر است.
- زاویه: از آنجا که 7- منفی است و 24i مثبت است، میدانیم که رو به عقب و بالا حرکت میکنیم یعنی از زاویه 90 عبور کردهایم. به بیان ریاضی atan(24/-7) = 106.2 درجه است. باید در ذهن داشته باشیم که ما در ربع دوم هستیم و حدس اولیه ما دوباره تأیید میشود.
با این که ما همواره میتوانیم به وسیله فرمولهای ریاضی محاسبه کنیم، اما داشتن شهود در مورد چرخشها و مقیاسبندیها برای بررسی نتایج به دست آمده مفید است. اگر زاویه به دست آمده کمتر از 90 درجه میبود، یا بزرگی حاصل برابر با 25 نبود، میدانستیم که خطایی در محاسبات ریاضی ما رخ داده است.
تقسیم مختلط
تقسیم متضاد ضرب است، همان طور که تفریق متضاد جمع است. زمانی که اعداد مختلط را تقسیم میکنیم (x تقسیم بر y) موارد زیر را داریم:
- تفریق زوایا:
زاویه (z) = زاویه (x) – زاویه (y)
- تقسیم بزرگی:
به نظر درست میآید. اینک آن را عملاً انجام میدهیم:
شاید از خود بپرسید اینک باید از کجا شروع کنیم؟ ما در عمل چگونه تقسیم را انجام میدادیم؟ تقسیم اعداد جبری معمولی خود وحشتانگیز است، چه رسد که عدد عجیب i نیز اضافه شده است؛ اما خوشبختانه راه میانبری وجود دارد.
معرفی مزدوجهای مختلط
نخستین کار ما در تقسیم، تفریق زاویهها است. این کار به این صورت انجام میگیرد که باید متضاد کاری که در ضرب انجام دادیم عمل کنیم. یعنی باید یک زاویه منفی را جمع کنیم تا بتوانیم تفریق نماییم.
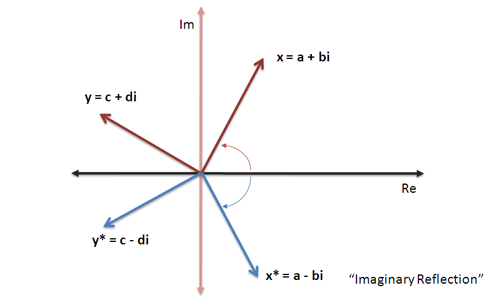
به جای z = a + bi عدد z* = a – bi را در نظر بگیرید که «مزدوج مختلط» نامیده میشود. این عدد بخش حقیقی دارد؛ اما بخش موهومی آن در بعد موهومی بازتاب یافته است. مزدوج یا «بازتاب موهومی» بزرگی برابری دارند؛ اما زاویه آنها مخالف هم است.
بنابراین ضرب کردن در a – bi همانند تفریق کردن یک زاویه است.
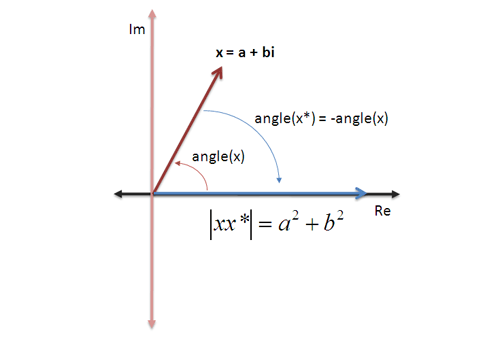
مزدوج مختلط با یک ستاره (*) یا خط تیرهای روی عدد مشخص میشود. ریاضیدانها به صحبت در مورد این روشهای نمادگذاری علاقهمند هستند. در هر صورت مزدوج، عدد مختلطی است که بخش موهومی آن معکوس شده است:
z = a + bi
دقت کنید که z لزوماً نمیبایست منفی باشد. اگر z = 3 – 4i باشد در این صورت z* = 3 + 4i است.
ضرب کردن در مزدوج
اگر بخواهیم عددی را در مزدوج خود ضرب کنیم چه رخ میدهد؟ یعنی حاصلضرب z* × z چه مقدار است؟ بدون هیچ فکری میتوانیم رابطه زیر را در نظر بگیریم:
بنابراین 1 (یعنی عدد حقیقی) را در نظر گرفته، زاویه (z) را اضافه میکنیم و سپس زاویه (*z) را نیز میافزاییم. اما این زاویه اخیر منفی است پس باید عمل تفریق صورت بگیرد. بنابراین نتیجه نهایی ما باید یک عدد حقیقی باشد، چون زاویهها همدیگر را خنثی کردهاند. عدد باید به صورت باشد، زیرا مقیاس را دو برابر کردهایم.
اینک مثالی را بررسی میکنیم:
ما چنان که انتظار داشتیم، یک عدد حقیقی داریم. علاقهمندان ریاضیات میتوانند فرمول جبری را نیز بررسی کنند:
میبینیم که نتیجه هیچ بخش موهومی ندارد و بزرگی آن دو برابر شده است. درک مزدوج مختلط به عنوان یک «چرخش منفی» به ما امکان میدهد که این نتایج را به روشی متفاوت پیشبینی کنیم.
مقیاسبندی اعداد
زمانی که یک عدد ( مانند z) را در مزدوج آن (*z) ضرب میکنیم، در واقع آن را به مقیاس |*z| میرسانیم. برای معکوس سازی این تأثیر میتوانیم آن را بر |z| تقسیم کنیم و برای فشرده کردن عدد به اندازه |z|، باید مجدداً تقسیم دیگری انجام دهیم. در نتیجه، باید عدد اصلی را پس از ضرب کردن در مزدوج، بر |z| × |z| تقسیم کنیم.
نمایش شیوه تقسیم
قبلاً از انجام تقسیم طفره رفتیم، ولی روش کار را اکنون نشان میدهیم. اگر بخواهیم تقسیم زیر را انجام دهیم:
میتوانیم به صورت شهودی آن را به صورت زیر انجام دهیم:
به اندازه زاویه مقابل چرخش میدهیم: ضرب در (1 – i) به جای (1+i)
تقسیم بر مجذور بزرگی یعنی تقسیم بر
پاسخ بر اساس رویکرد فوق چنین است:
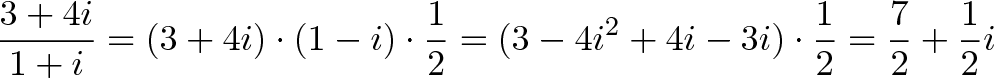
با استفاده از روش سنتیتر که در آن صورت و مخرج کسرها در مزدوج ضرب میشود، نتیجه به صورت زیر خواهد بود:
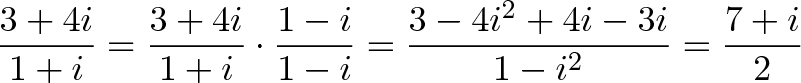
ما به طور سنتی فکر میکنیم که «کافی است دو طرف را در مزدوج مختلط ضرب کنیم»، اما نمیدانیم که تقسیم مختلط دقیقاً به چه معنا است.
اینک ما میدانیم که چه اتفاقی میافتد. تقسیم، همان تفریق یک زاویه و کاهش بزرگی عدد است. با ضرب کردن صورت و مخرج در مزدوج، در واقع زاویه را تفریق میکنیم که باعث میشود صورت تبدیل به یک عدد حقیقی شود. همچنین صورت و مخرج را دقیقاً به یک مقدار بزرگ میکنیم و از این رو تأثیر آن خنثی میشود. نتیجه این است که تقسیم به ضرب در صورت تبدیل میشود.
هر دو رویکرد به پاسخ صحیح منتهی میشوند و با این که در اغلب موارد رویکرد دوم آموزش داده میشود، اما همیشه دانستن دو روش حل برای بررسی درستی پاسخ ایده خوبی محسوب میشود.
ترفندهای ریاضیاتی دیگر
اینک که مزدوج را شناختیم، چندین خصوصیت هست که باید در نظر داشته باشیم:
رابطه اول معنیدار است. هنگام جمعکردن دو عدد و بازتاب (مزدوج)، نتیجه همانند جمع زدن دو بازتاب است. روش دیگر برای تصور این رابطه آن است که دو عدد لغزش مییابند و سپس جهت معکوس میگیرند یعنی گویی هر دو عدد در جهت معکوس لغزش یافتهاند.
خصوصیت دوم کمی دشوارتر است. با این که میتوانیم از فرمولهای جبری استفاده کنیم؛ اما شاید توضیح شهودی بهتر باشد:
معنی نتیجه چنین است:
- بزرگیها را در هم ضرب کنید: |x| × |y|
- زاویهها را با هم جمع زده و مزدوج را به دست آورید تا معکوس زاویه (x) + زاویه (y) به «- زاویه (x) + - زاویه (y)» تبدیل میشود.
و *x ضرب در *y به معنی زیر است:
- ضرب در بزرگی:
|x| × |y| (همانند رابطه فوق است).
- افزودن زاویه مزدوج:
زاویه (x) + زاویه (y) = - زاویه (x) + - زاویه (y)
در هر مورد بزرگی و زاویه برابری داریم و لازم نیست از توضیح جبری سنتی استفاده کنیم. جبر خوب است؛ اما همواره بهترین توضیح را ارائه نمیکند.
یک مثال ساده
مزدوجسازی روشی برای لغو کردن یک چرخش است. آن را میتوان به صورتهای زیر در نظر گرفت:
- فرض کنید 3، 10، 15.75 و 23.50 تومان در حساب خود سپردهگذاری کردهایم. چه تراکنشی همه این مبالغ را خنثی میکند؟ برای یافتن معکوس باید آنها را با هم جمع کرده و در 1- ضرب کنیم.
- فرض کنید خطی را با چند عمل ضرب به صورت , , و چرخش میدهیم. کدام چرخش این چرخشها را خنثی میکند؟ برای یافتن معکوس، باید اعداد مختلط را در هم جمع کرده و مزدوج نتیجه را در نظر بگیریم.
دیدیم که مزدوج *z روشی برای خنثیسازی تأثیر چرخش z است، همان طور که عدد منفی تأثیر جمع را خنثی میکند. اما باید توجه کنید که برای خنثیسازی تأثیر مقیاسبندی باید بر |z| × |z| نیز تقسیم کنید.
سخن پایانی
مسائل ریاضیاتی که در این نوشته مطرح کردیم، موضوع جدیدی محسوب نمیشوند؛ اما شاید تاکنون هرگز توجه نکرده بودید که چرا مزدوج مختلط را باید مورد استفاده قرار دهید. چرا a – bi باشد و a + bi- نباشد. مزدوجهای مختلط یک گزینه تصادفی محسوب نمیشوند، بلکه تصویری بازتاب یافته از منظر موهومی هستند که دقیقاً زاویه متضادی دارند.
مشاهده اعداد موهومی به صورت چرخش باعث میشود که ذهنیت جدیدی برای حل مسائل داشته باشیم. فرمولهای این چنینی میتوانند درکی شهودی از مسائل هر چند برای موضوعات عجیبی مانند اعداد مختلط به دست بدهند.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- اعداد مختلط – به زبان ساده
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- آموزش ریشه یابی و ترسیم اعداد مختلط در متلب
- اعداد گویا — به زبان ساده
- اعداد موهومی: راهنمای تصویری و شهودی — به زبان ساده
==













با سلام. مطلب خیلی خوب بود ولی بنظرم یه جای کار ایراد داشت :
مقیاسبندی اعداد
زمانی که یک عدد را در مزدوجش (*z) ضرب میکنیم، در واقع آن را به مقیاس |*z| میرسانیم. برای معکوس سازی این تأثیر میتوانیم آن را بر |z| تقسیم کنیم و…
ش در مزدوج فکر کنم اضافیست و این اضافه بودن باعث پیچیدگی و نفهمیدن مطلب میشود. من خیلی فکر کردم تا فهمیدم این پاراگراف چی میگه.
امیدوارم درست گفته باشم.
با سلام،
متن بازبینی و ویرایش شد،
با تشکر از همراهی شما با مجله فرادرس