ریاضی

ضرب ماتریس ها – به زبان ساده

۱۵۲۹۱۷ بازدید
آخرین به‌روزرسانی: ۱۷ آذر ۱۴۰۳
زمان مطالعه: ۵ دقیقه
دانلود PDF مقاله
ضرب ماتریس ها – به زبان سادهضرب ماتریس ها – به زبان ساده

ماتریس، آرایش منظمی از اعداد است که در جدولی از سطرها و ستون‌ها آرایش یافته‌اند. در این مطلب قصد داریم تا اصول ضرب دو ماتریس را بیان کنیم. البته در مواردی می‌توان از ویژگی‌های یک ماتریس همچون ترانهاده در ضرب ماتریس‌ها بهره برد. اگر می‌خواهید اطلاعات بیشتری در مورد ماتریس‌ها کسب کنید می‌توانید به نوشته  «ماتریس ها — به زبان ساده» از مجله فرادرس مراجعه کنید. ماتریس زیر با دو سطر و سه ستون را می بینید:

997696

[64241−98]\begin{bmatrix}6 & 4 & 24 \\ 1 & -9 & 8 \end{bmatrix}

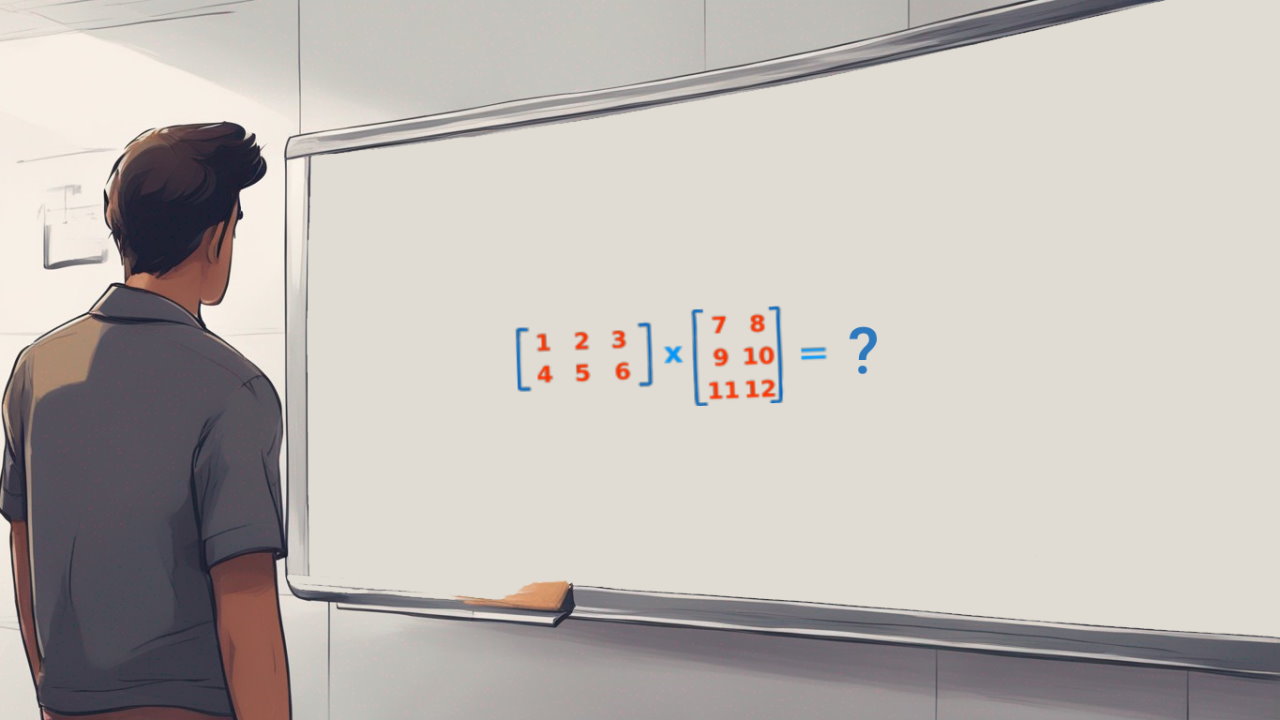
اینک می‌خواهیم عددی را در این ماتریس ضرب کنیم. باید بدانید که ضرب عدد منفرد در یک ماتریس کار آسانی است. برای انجام این کار کافی است آن عدد را در تک تک درایه‌های ماتریس ضرب کنیم و با نتایج حاصل یک ماتریس جدید تشکیل دهیم. برای مثال در تصویر زیر می بینید که چگونه با ضرب عدد 2 در درایه اول، عدد 8 برای درایه اول ماتریس حاصلضرب به دست آمده است:

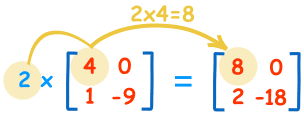
ضرب ماتریس

محاسبات ضرب همه درایه‌های ماتریس به صورت زیر است:

2 × 4 = 8               2 × 0 = 0
2 × 1 = 2               2 × -9 = -18

به عددی که در یک ماتریس ضرب می‌شود، «اسکالر» (scalar) گفته می‌شود. برای مثال در تصویر فوق عدد 2 اسکالر بوده است. به ضرب عدد اسکالر در یک ماتریس نیز ضرب اسکالر گفته می شود. در مقابل این نوع ضرب، مفهوم «ضرب داخلی» یا ضرب درونی (dot Product) قرار دارد که در ادامه آن را بیشتر توضیح می‌دهیم. در نوشتاری دیگر به مفهوم متفاوتی از اسکالر که برای ماتریس‌ها تعریف می‌شود پرداخته‌ایم.

ضرب یک ماتریس در ماتریس دیگر

اما برای ضرب یک ماتریس در ماتریسی دیگر، باید ضرب داخلی یا  نقطه‌ای سطرها و ستون‌ها را پیدا کنیم. شاید از خود بپرسید ضرب داخلی چگونه است و چه تفاوتی با ضرب معمولی دارد. در ضرب داخلی به جای ضرب اعداد، سطر‌ها و ستون‌ها در هم ضرب می شوند. با یک مثال به توضیح آن می پردازیم:

در مثال ماتریس زیر برای یافتن جواب ضرب داخلی سطر اول و ستون اول به صورت زیر عمل می‌کنیم:

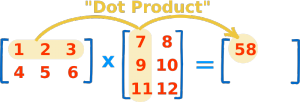
ضرب ماتریس

در ضرب داخلی، درایه‌های سطر و ستون های مرتبط را در ماتریس های مختلف در هم ضرب می کنیم و سپس پاسخ‌های به دست آمده را باهم جمع می‌زنیم. در مثال فوق محاسبات به صورت زیر است::

( 1, 2, 3 ) • ( 7, 9, 11 ) = 1×7 + 2×9 + 3×11 = 58

دو عضو اول سطر و ستون مربوط به ماتریس‌های اول دو دوم را با هم تطبیق می دهیم (1 و 7) و آن‌ها را در هم ضرب می کنیم. سپس همین کار را برای عضو‌های دوم (2 و 9) و سوم (3 و 11) انجام می دهیم، و در نهایت همه پاسخ‌ها را با هم جمع می‌زنیم.

اگر می‌خواهید مثال دیگری را ببینید، در تصویر زیر همین کار را برای سطر اول از ماتریس اول و ستون دوم ماتریس دوم انجام داده‌ایم:

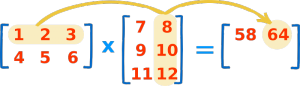
ضرب ماتریس

( 1, 2, 3 ) • ( 8, 10, 12 ) = 1×8 + 2×10 + 3×12 = 64

همین عمل را برای سطر دوم و ستون اول انجام می دهیم:

( 4, 5, 6 ) • ( 7, 9, 11 ) = 4×7 + 5×9 + 6×11 = 139

و همچنین برای سطر دوم و ستون دوم:

( 4, 5, 6 ) • ( 8, 10, 12 ) = 4×8 + 5×10 + 6×12 = 154

و در نهایت ماتریس زیر به دست می آید:

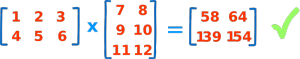
اینک کار ضرب دو ماتریس پایان یافته است.

چرا ضرب داخلی به این شکل انجام می‌گیرد؟

گرچه در نگاه نخست ممکن است این نوع ضرب کردن، روشی غیر عادی و پیچیده به نظر بیاید؛ اما عمل ضرب داخلی در محاسبه‌های مختلف امری مهم و ضروری محسوب می‌شود. در ادامه مثالی کاربردی ارائه می‌کنیم تا با دلیل این که چرا ماتریس ها را این گونه در هم ضرب می کنیم، بهتر آشنا شوید.

مثال: تصور کنید یک رستوران در طی روزهای مختلف هفته، غذاهای متفاوتی را در تعداد گوناگون به فروش می‌رساند. فهرست قیمت غذاهای این رستوران چیزی شبیه زیر است:

  • کباب به قیمت سه دلار
  • مرغ به قیمت چهار دلار
  • غذای سبزیجات به قیمت دو دلار

و جدول زیر، تعداد فروش هرکدام از غذاها در 4 روز است:

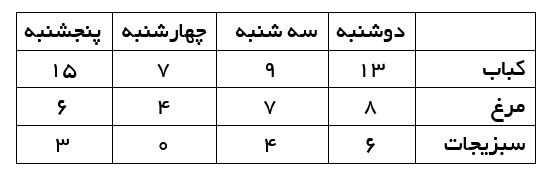
خب، اکنون می‌دانیم که درآمد فروش برای روز دوشنبه اینگونه محاسبه می‌شود:

مجموع فروش = قیمت مجموع فروش کباب + قیمت مجموع فروش مرغ + قیمت مجموع فروش غذای سبزیجات

3$ × 13 + 4$ × 8 + 2$ × 6 = 83$

خب، این در واقع «ضرب داخلی» قیمت‌ها در تعداد فروش هر کدام از آنها است. به عبارت دیگر:

( 3$ , 4$ , 2$ ) • ( 13 , 8 , 6 ) = 3$×13 + 4$×8 + 2$×6 = 83$

ما قیمت و تعداد فروش را باهم تطبیق می دهیم، هرکدام را ضرب می کنیم، سپس نتایج را باهم جمع می کنیم.

به عبارت دیگر:

  •  فروش برای روز دوشنبه از این قرار بود: کباب: 3$ × 13 = 39$، مرغ: 4$ × 8 = 32$ و غذای سبزیجات: 2$ × 6 = 12. که مجموع آنها می‌شود:

39$ + 32$ + 12$ = 83$.

  •  و برای روز سه شنبه:

3$ × 9 + 4$ × 7 + 2$ × 4 = 63$

  •  و برای روز چهارشنبه:

3$ × 7 + 4$ × 4 + 2$ × 0 = 37$

  •  و برای روز پنجشنبه:

3$ × 15 + 4$ × 6 + 2$ × 3 = 75$

پس، تطبیق قیمت هر محصول با تعدادش مهم است. احتمالاً اکنون می دانید که چرا ما از "ضرب داخلی" استفاده می کنیم و با اهمیت آن در این گونه محاسبات بیشتر آشنا شدید. در تصویر زیر فرم کلی ضرب داخلی ماتریس‌های تعداد فروش و قیمت غذاها ارائه شده است:

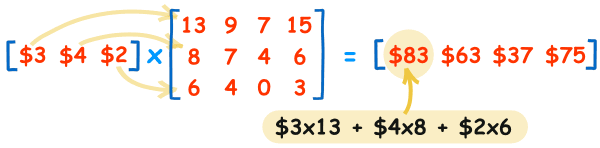
بدین ترتیب می‌بینیم که صاحب رستوران در روز دوشنبه به مقدار 83$، در روز سه‌شنبه به میزان 63$ و ... فروش داشته است.

سطرها و ستون‌ها

برای نشان دادن تعداد سطر‌ها و ستون‌های یک ماتریس، معمولا آن را به شکل (ستون‌ها × سطرها) می نویسیم.

مثال: ماتریس 3×2 (دو سطر و سه ستون) به شکل زیر است:

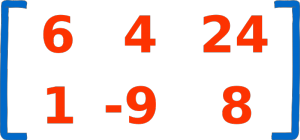
هنگامی که ضرب داخلی را روی دو ماتریس انجام می‌دهیم باید در دو ماتریس شرایط خاصی وجود داشته باشد تا بتوانیم این نوع ضرب را انجام دهیم:

  • تعداد ستون های ماتریس اول باید با تعداد سطرهای ماتریس دوم برابر باشد.
  • و سطرهای ماتریس حاضلضرب به تعداد سطرهای ماتریس اول و ستون‌های آن نیز به تعداد ستون های ماتریس دوم سطر خواهد بود.

مثال:

در این مثال ما یک ماتریس 3×1 را در یک ماتریس 4×3 ضرب کردیم (دقت کنید که 3 ها برابرند)، و نتیجه یک ماتریس 4×1 بود.

به طور کلی:

برای ضرب یک ماتریس m×n در یک ماتریس n×p، تعداد nها باید باهم برابر باشند و نتیجه ضرب، یک ماتریس m×p خواهد بود.

ترتیب در ضرب ماتریس‌ها

در ضرب معمولی با قانون زیر که قانون جابجایی نام دارد، آشنا هستیم:

3 × 5 = 5 × 3

اما این قانون عموما برای ماتریس ها صدق نمی‌کند چون ضرب ماتریس ها خاصیت جابجایی ندارد، یعنی:

AB ≠ BA

هنگامی که ما جای ماتریس ها را در ضرب عوض می کنیم، پاسخ معمولاً متفاوت است.

مثال:

مشاهده کنید که تغییر ترتیب ماتریس‌ها، چگونه باعث تغییر یافتن نتیجه می‌شود:

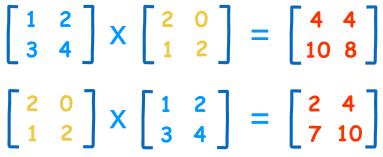
اما در یک حالت این تغییر ترتیب باعث ایجاد تغییر در نتیجه حاصلضرب داخلی ماتریس‌ها نمی شود و آن زمانی است که یکی از ماتریس‌ها ماتریس همانی (یا یکّه) باشد.

ماتریس همانی

در مطلب «ماتریس همانی و ماتریس یکانی | به زبان ساده» در مورد «ماتریس همانی» یا ماتریس یکّه (Identity Matrix) صحبت کردیم. ماتریس همانی، ماتریسی است که همه درایه‌های روی قطر اصلی آن برابر با عدد 1 هستند:

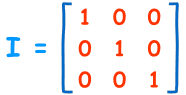
یک ماتریس همانی 3×3

ماتریس همانی خصوصیاتی به شرح زیر دارد:

  • این ماتریس «مربع» است (تعداد سطرها و ستون‌هایش برابر است)،
  • بر روی قطر ماتریس همانی تنها عدد 1 و در بقیه نقاط عدد 0 وجود دارد،
  •  نماد این ماتریس، حرف بزرگ انگلیسی I است.

مانریس همانی، ماتریس ویژه‌ای است، چرا که هر ماتریس دیگری را در آن ضرب کنیم، پاسخ همان ماتریس اولیه خواهد بود:

A × I = A

I × A = A

آزمون ضرب ماتریس ها

در این قسمت به منظور درک بهتر ضرب ماتریس ها، تعدادی پرسش چهار گزینه‌ای به صورت آزمون تهیه شده است.

حاصل 6(−25)6 \left(\begin{array}{c}-2\\ 5 \end{array}\right) برابر است با:

(−1230)\left(\begin{array}{c}-12\\ 30\end{array}\right)

(1230)\left(\begin{array}{c} 12\\ 30\end{array}\right)

(12−30)\left(\begin{array}{c} 12\\ -30\end{array}\right)

(30−12)\left(\begin{array}{c} 30 \\ -12 \end{array}\right)

پاسخ تشریحی

به هنگام ضرب ماتریس در عددی ثابت، این عدد در تک تک آرایه‌ها به صورت جداگانه ضرب می‌شود:

6(−25)=(−1230)6 \left(\begin{array}{c}-2\\ 5 \end{array}\right) = \left(\begin{array}{c}-12\\ 30\end{array}\right)

حاصل [−316−2](2−1)\begin{bmatrix}-3 & 1 \\ 6 & -2 \end{bmatrix} \left(\begin{array}{c}2\\ -1 \end{array}\right) کدام است؟

(14−7)\left(\begin{array}{c} 14 \\ -7 \end{array}\right)

(−714)\left(\begin{array}{c} -7 \\ 14 \end{array}\right)

(7−14)\left(\begin{array}{c} 7 \\ -14 \end{array}\right)

(−7−14)\left(\begin{array}{c} -7 \\ -14 \end{array}\right)

پاسخ تشریحی

حاصل [−316−2](2−1)\begin{bmatrix}-3 & 1 \\ 6 & -2 \end{bmatrix} \left(\begin{array}{c}2\\ -1 \end{array}\right) ماتریسی دو در یک است و به صورت زیر نوشته می‌شود:

[−316−2](2−1)=((−3)(2)+(1)(−1)(6)(2)+(−2)(−1))=(−714)\begin{bmatrix}-3 & 1 \\ 6 & -2 \end{bmatrix} \left(\begin{array}{c}2\\ -1 \end{array}\right) =\left(\begin{array}{c}(-3 ) ( 2) + ( 1 ) ( -1 ) \\ (6) ( 2) + ( -2 ) ( -1 )\end{array}\right) = \left(\begin{array}{c} -7 \\ 14 \end{array}\right)

حاصل 5[−24−30](15)5 \begin{bmatrix}-2 & 4 \\ -3 & 0 \end{bmatrix} \left(\begin{array}{c} 1 \\ 5 \end{array}\right) برابر است با:

(90−15)\left(\begin{array}{c} 90 \\-15 \end{array}\right)

(−90−15)\left(\begin{array}{c} -90 \\ -15 \end{array}\right)

(90−15)\left(\begin{array}{c} 90 \\ -15 \end{array}\right)

(−9015)\left(\begin{array}{c} -90 \\ 15 \end{array}\right)

پاسخ تشریحی

در این مسئله باید حاصل‌ضرب عددی ثابت در دو ماتریس را به‌دست آوریم. برای محاسبه 5[−24−30](15)5 \begin{bmatrix}-2 & 4 \\ -3 & 0 \end{bmatrix} \left(\begin{array}{c} 1 \\ 5 \end{array}\right) ابتدا عدد ۵ را در ماتریس [−24−30]\begin{bmatrix}-2 & 4 \\ -3 & 0 \end{bmatrix} ضرب، سپس نتیجه به‌دست آمده را در ماتریس (15)\left(\begin{array}{c} 1 \\ 5 \end{array}\right) ضرب می‌کنیم. 

5[−24−30]=[−1020−150]5 \begin{bmatrix}-2 & 4 \\ -3 & 0 \end{bmatrix} = \begin{bmatrix}-10 & 20 \\ -15 & 0 \end{bmatrix}

در ادامه، ماتریس [−1020−150]\begin{bmatrix}-10 & 20 \\ -15 & 0 \end{bmatrix} را در (15)\left(\begin{array}{c} 1 \\ 5 \end{array}\right) ضرب می‌کنیم:

[−1020−150](15)=((−10)(1)+(20)(5)(−15)(1)+(0)(5))=(90−15)\begin{bmatrix}-10 & 20 \\ -15 & 0 \end{bmatrix} \left(\begin{array}{c} 1 \\ 5 \end{array}\right) =\left(\begin{array}{c}(-10 ) (1) + ( 20 ) ( 5 ) \\ (-15) ( 1 ) + ( 0 ) ( 5 )\end{array}\right) = \left(\begin{array}{c} 90 \\ -15 \end{array}\right) 

اگر [−1021x−1][y22]=[−11]\begin{bmatrix}-1 & 0 & 2 \\ 1 & x & -1 \end{bmatrix} \begin{bmatrix}y \\ 2 \\ 2 \end{bmatrix} = \begin{bmatrix}-1 \\ 1 \end{bmatrix} باشد، حاصل x+yx + y کدام است؟ 

۵-

۴-

۴

۵

پاسخ تشریحی

برای به‌دست آوردن مقادیر xx و yy ابتدا باید دو ماتریس [−1021x−1]\begin{bmatrix}-1 & 0 & 2 \\ 1 & x & -1 \end{bmatrix} و \begin{bmatrix}y \\ 2 \\ 2 \end{bmatrix} را با یکدیگر ضرب کنیم:

[−1021x−1][y22]=[(−1)(y)+(0)(2)+(2)(2)(1)(y)+(2)(x)+(−1)(2)]=[−y+4y+2x−2]\begin{bmatrix}-1 & 0 & 2 \\ 1 & x & -1 \end{bmatrix} \begin{bmatrix}y \\ 2 \\ 2 \end{bmatrix} = \begin{bmatrix} ( -1 ) ( y ) + ( 0 ) ( 2 ) + ( 2 ) ( 2 ) \\ ( 1) ( y ) + ( 2 ) ( x ) + ( -1) ( 2 ) \end{bmatrix} =\begin{bmatrix} -y + 4 \\ y+2x-2 \end{bmatrix}

در ادامه، ماتریس [−y+4y+2x−2]\begin{bmatrix} -y + 4 \\ y+2x-2 \end{bmatrix} را برابر ماتریس [−11]\begin{bmatrix}-1 \\ 1 \end{bmatrix} قرار می‌دهیم و مقدارهای xx و yy را به‌دست می‌آوریم:

[−y+4y+2x−2]=[−11]\begin{bmatrix} -y + 4 \\ y+2x-2 \end{bmatrix} =\begin{bmatrix}-1 \\ 1 \end{bmatrix}

مقدار xx برابر ۱- و مقدار yy برابر ۵ به‌دست می‌آید. در نتیجه، حاصل x+yx + y برابر ۴ است. 

اگر A=[2−13−2]A = \begin{bmatrix} 2 & -1 \\ 3 & -2 \end{bmatrix} باشد، ماتریس A7−A4A ^ 7 - A ^ 4 کدام است؟

[1031]\begin{bmatrix} 1 & 0\\ 3 & 1 \end{bmatrix}

[1−13−3]\begin{bmatrix} 1 & -1\\ 3 & -3 \end{bmatrix}

[−113−3]\begin{bmatrix} -1 & 1\\ 3 & -3 \end{bmatrix}

[12−2−3]\begin{bmatrix} 1 & 2 \\ -2 & -3 \end{bmatrix}

پاسخ تشریحی
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.

اگر A=[1012]A = \begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix}  و رابطه A2=αA+βIA ^ 2 = \alpha A + \beta I برقرار باشد، مقدار α+β\alpha + \beta کدام است؟ 

۱

صفر

۱-

۲

پاسخ تشریحی
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.

اگر II ماتریس واحد و A=[0−110]A = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}، ماتریس (A+I)2( A + I ) ^ 2 کدام است؟ 

−2I- 2 I

−2A- 2 A

2I2 I

2A2 A

پاسخ تشریحی
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.

اگر A=[0110]A = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} باشد، کدام یک از ماتریس‌های زیر برابر A نیست؟

A1387A ^ { 1387}

A1388A ^ { 1388}

A1389A ^ { 1389}

A2009A ^ { 2009 }

پاسخ تشریحی
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
محصول، خدمات یا برند خود را در مجله فرادرس معرفی کنید.
کلیک کنید
بر اساس رای ۸۰۸ نفر
آیا این مطلب برای شما مفید بود؟
اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.
منابع:
mathsisfun
دانلود PDF مقاله
https://b.fdrs.ir/345
مطالب مرتبط
۶۳ دیدگاه برای «ضرب ماتریس ها – به زبان ساده»
جواد

عالی

پاسخ
زهرا

دمت گرم

پاسخ
علی

سلام ممنون🩵💙

پاسخ
محمد

ممنون از زحمتی که کشیدید

پاسخ
رضا

بسیار عالی و مفید بود ممنون

پاسخ
محمد

عالی بود

پاسخ
نقوی

بسیار عالی و فوق العاده است.

پاسخ
امید

سپاسگزارم

یه کاربر

خیلی خوب بود متشکرم
ای کاش تقسیم شون رو هم میذاشتید

پاسخ
ارغوان

سلام ممنون از توضیحات. کاش موزیک نذارید رو ویدیو ها

پاسخ
سید عزت

ببخشید! از سال ۹۷ هی میگید آموزش تحلیل ماتریسی سازه‌ها قرار اس آماده و پخش بشه ولی تا الان که ۱۴۰۲ اس نشده، لطفاً حداقل لینک مریوطه‌اش را از این صفحه بردارید🙏

سهیل بحر کاظمی

با سلام؛

از ارائه بازخورد شما بسیار سپاس‌گزاریم. متن بازبینی و اصلاح شد.

با تشکر از همراهی شما با مجله فرادرس

عارفه

دکتر محمدیان بی شک نقطه عطف دوران دانشجویی من هستند،تدریس فوق العاده ایشون تابه الان چندین بار باعث نمرات بالای من شده وخیلی مواقع کمکم کرده،امیدوارم هرجاهستند تنشون سالم باشه و موفقیت هاشون روزافزون
سپاس از ایشون و تیم فرادرس

پاسخ
باران

چه زمانی ضرب دو ماتریس با هم برابرند؟ یعنی AB=BA

پاسخ
سید سراج حمیدی

سلام.
اگر دو ماتریس مربعی و هم‌بعد AA و BB را داشته باشیم، در شرایط زیر تساوی AB=BAA B = B A برقرار خواهد بود:
۱. اگر A=BA = B.
۲. اگر A=cIA=cI یا B=cIB = c I که در آن‌ها، cc یک عدد حقیقی است.
۳. اگر AA و BB، هردو، ماتریس‌هایی قطری باشند.
۴. ماتریس وارون‌پذیر PP به‌گونه‌ای وجود داشته باشد که P−1APP^{-1}AP و P−1BPP^{-1}BP هردو قطری باشند.
شاد و پیرووز باشید.

مریم حسن پور

سلام و درود در متن احتمالا اشتباه تایپی شده به جای کافی مافی نوشته شده .
با سپاس همیشگی از سایت فرادرس???

پاسخ
رضا مقدری

سلام، وقت شما بخیر؛

این اشتباه تایپی اصلاح شد.

از اینکه با مجله فرادرس همراه هستید و با نظرات خود ما را در بهتر شدن آن یاری می‌دهید از شما سپاسگزاریم.

محمد

خدا پدرتو بیامرزه عالی

پاسخ
پرویز پاوندمهر

آقا ممنون خلاصه ومفید بود آفرین بر شما

پاسخ
علیرضا

توضیح فوق العاده واضحی بود !
این کلیپ 5 دقیقه ای شما مفهوم تر از توضیح 90 دقیقه ای استاد ما بود !
بسیار ممنون

پاسخ
كيهان

دانشگاه و مدرسه جاي اينجور مدرس هاي با لياقتيه

پاسخ
زهرا

خیلی ممنون خداخیرتون بده یه جاشومشکل داشتم تازه فهمیدم

آرش

به عددی که در ماتریس ضرب میشه اسکالر نمی گن به ماتریس قطری که اعداد رو قطر ان مساوی یکدیگر باشند ماتریس اسکالر می گویند

پاسخ
سید سراج حمیدی

سلام. در متن به ماتریس اسکالر اشاره نشده است. اسکالر به معنای عدد و ماتریس اسکالر دو مفهوم متفاوت هستند و آنچه در متن نوشته شده، صحیح است.
از همراهی‌تا با مجله فرادرس سپاسگزاریم.

زهرا

بسیار روان
بسیار عالی
موتوشکرم ?

پاسخ
najafisaghra.83.com@gmail.com

: دو ماتریس 2 در 2 را از اعداد صحیح پر کرده و حاصلضرب دو ماتریس را در خروجی نمایش دهد جواب اینو بگید توووورو خداااااا

سعید

خوب بود

پاسخ
'ali'

نمیدونم چرا اینارو از کتب درسی دبیرستان حذف کردن
میخوان ما رو بدبخت کنن توی دانشگاه

پاسخ
ارش

گلم اینا دقیقا در فصل اول کتاب هندسه اس رشته ریاضی

Kingnight

خداییش حال کردم حلالتون

پاسخ
اميرعباس

عالي ??

پاسخ
ارش

گلم اینا دقیقا در فصل اول کتاب هندسه اس رشته ریاضی

زهرا

سپاس.عالی

پاسخ
neda

من اخرش نفمیدم ماتریس۳در۳چ جوری بدست میاد

پاسخ
جواد

اگه منظورت نحوه ضرب دو تا ماتریس هست که بالا واضح توضیح دادن دیگه. اگه منظورت اینه که ماتریس ۳ در ۳ کلا چی هست و چطوری همچین چیزی مطرح میشه باید بگم خیلی راه ها و موارد وجود داره که باعث ایجاد یک ماتریس میشه. مثلا وقتی میخوان یک خرپا رو توی عمران یا مکانیک تحلیل کنن به ماتریس برخورد میکنن. یا وقتی میخوان یک سری معادله خطی رو حل کنن یا حتی وقتی میخوان نیرو های وارد بر ذرات یک جسم رو بررسی کنن. خلاصه ماتریس تویه مهندسی برق و مکانیک و عمران و ……. خیلی زیاد به کار میره. شاید یکی از مهمترین بخش های ریاضی باشه

علی

خخخخخ حال کردم عین چی تو گِل گیر کرده بودم یاد گرفتم لامصبا تو کتبا توضیح نمیدن که چطوریه یچیزی نوشتن
با این وجود سرانه مطلاعه تو ایران 24 ساعته همه سرشون تو گوشی جوک میخونن مطلب فورارد میکنن نمیدونم از جون درختا چی میخوان اینا بازم تشکر

پاسخ
فرزاد

بسیار عالی.ممنون

پاسخ
محمد

دمتون گرم خدا خیرتون بده
شما از استاد دانشگاه بهتر توضیح دادید به خدا

پاسخ
سارا

سلام
واقعا ممنونم از این طرز بیان ساده وکاملا روان واقعا دستتون درد نکنه و خدا خیرتون بده

پاسخ
zahra

خیلی ممنون

پاسخ
سعید

عالی بود خدا خیرتون بده

پاسخ
banoo

عالی بود دمتون گرم،به هیچ روشی نمیفهمیدم ولی الان کاملا یادگرفتم،خداخیرتون بده

پاسخ
Vahide

عالی بووووود. هر چی از خدا میخواین بهتون بده

پاسخ
Amir

ممنون از اموزش عالیتون

پاسخ
ali

عالی و بدون نقص

پاسخ
Yasna

سلام چقدر روشن و قابل فهم توضیح دادین کاش معلم ما هم روش تدریسش اینجوری بود.

پاسخ
مهدی

عالی بود

پاسخ
ملي آنا

با سپاس فراوان. مطالب بسيار عالي و آموزنده بود . روش تدريس شما بي نظيره . !!!!!!

پاسخ
محمدرضا

عالي

پاسخ
farid

بسیار خلاصه ومفید بود باسپاس

پاسخ
khashayar

نحوه توضیح درس ها در blog.faradars فوق العادست همین راهو ادامه و گسترشش بدین آینده روشنی دارین …قشنگ شیر فهم میکنه طرز بیان درس ها

پاسخ
Aliof

عاااااالی بود .خیلی کارامد بود وبا زبان ساده گفته شده بود

پاسخ
Zahrw

عالـــــــــــــــــــــــــی بوووووود??

پاسخ
حمید

خیلی عالی بود مرسی

پاسخ
یاسمن

وای عالی بود دستتون درد نکنه

پاسخ
فاطمه

خیلی درسنامتون عالیه من که استفاده کردم ممنون

پاسخ
سارا

خیلی ممنون از توضیحات روان و ساده.

پاسخ
آرمین

سلام ببخشید ضرب یک ماتریس در چه صورت خاصیت حذف پذیری داره؟مثلا در چه صورت مثلا در
A × B =A × C
ماتریسAرو از طرفین ساده کرد

مجید

سلام.
کارشناسی حسابداری میخوانم.
درس پژوهش 2 بحث سیمپلکس، واقعا فراموش کرده بودم ضرب ماتریسها رو.
خیلی ممنون، خیلی واضح توضیح دادید.

پاسخ
سبحان

متشکرم

پاسخ
hadis

خیلی خوب بود یعنی عااااالی بود. مرسی.

پاسخ
حسن

دمتون گرم
ساده و قابل درک

محمد علی امینی

خوب ولی کامل نیست
مثلاً نگفتید که ضرب ماتریس 2*2 با ماتریس 3*3 امکان پذیر نیست و در ضرب دو ماتریس باید حتماً تعداد ستونهای ماترس اول با تعداد سطرهای ماتریس دوم برابر باشد در غیر اینصورت قابل ضرب نیست. و موارد دیگر

نظر شما چیست؟

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *

برچسب‌ها
Matrix
Matrices
Matrix Row
dot product
ماتریس
Matrix usage
Matrix Column
Matrix Entries
Matrix members
ضرب عددی
Identity Matrix
ضرب داخلی
سطر ماتریس
ضرب اسکالر
ماتریس یکه
ضرب نقطه ای
Scalar Multiplication
ستون ماتریس
Order of Multiplication
ماتریس همانی
ضرب ماتریس ها
ریاضی عمومی ۲
ریاضی دانشگاه
کاربرد ماتریس
Use of matrix in real-life
نظم اعداد در ضرب
Multiply a matrix by a number
کاربرد ضرب داخلی
درایه های ماتریس
Dot product usage in real life
Multiply a matrix by a constant
Commutative Law of multiplication
Multiply a Matrix by another Matrix
ریاضیات پایه دانشگاه
How to multiply a matrix by a constant
ضرب ماتریس در عدد ثابت
قانون جا به جایی در ضرب
ضرب ماتریس در ماتریس دیگر
کاربرد ماتریس در دنیای واقعی
کاربرد ضرب داخلی در دنیای واقعی