خوشه بندی سلسله مراتبی (Hierarchical Clustering) – به همراه کدهای R
در دادهکاوی و آمار، «خوشهبندی سلسله مراتبی» (Hierarchical Clustering) به روشی گفته میشود که عمل دستهبندی و گروهبندی مشاهدات و دادهها را به صورت سلسله مراتبی انجام میدهد. نکتهای که این روش را نسبت به روشهای دیگر خوشهبندی مجزا میکند، وجود ترتیب و یک نگاه از بالا به پایین (یا از پایین به بالا) است که در این تکنیک وجود دارد.

برای انجام خوشهبندی سلسله مراتبی، الگوریتمهای مختلف و متنوعی طراحی و پیاده سازی شده است. به همین علت برای اجرای عملیات خوشهبندی از دستورات زبان برنامه نویسی R کمک گرفته تا خوشهبندی سلسله مراتبی را روی دادهها اجرا کنیم.
برای آشنایی بیشتر با مفاهیم اولیه خوشهبندی و توابع فاصله بهتر است مطلب آشنایی با خوشهبندی (Clustering) و شیوههای مختلف آن و فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در دادهکاوی را مطالعه کنید. همچنین به منظور آگاهی از ارزیابی نتایج خوشهبندی، مطالعه مطلبهای روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای درونی (Internal Index) و روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای بیرونی (External Index) خالی از لطف نیست.
خوشهبندی سلسله مراتبی (Hierarchical Clustering)
یکی از روشهای «یادگیری ماشین» (Machine Learning) که به «آموزش بدون نظارت» (Unsupervised Learning) شهرت دارد، تحلیل خوشهبندی (Clustering Analysis) است. در این روش، برعکس خوشه بندی k-میانگین، هر مشاهده ممکن است در بیش از یک خوشه قرار گیرد زیرا براساس سطوح مختلف فاصله، خوشهها تشکیل میشود. بنابراین هر خوشه ممکن است زیر مجموعه خوشه دیگر در سطحی از فاصله قرار گیرد. به هر حال خوشهبندی روش است که به کمک «ویژگیها» (Features) یا «صفتها» (Attributes) مشاهدات، آن را به گروههای مشابه طبقهبندی میکند.
انتخاب ویژگیهای مناسب برای این کار، یکی از مسائل مهمی است که باید در نظر گرفته شود. از طرف دیگر استانداردسازی دادهها نیز مطرح است تا مقیاس اندازهگیری صفت یا ویژگیها باعث انحراف تابع فاصله نشود. با توجه به بار محاسباتی زیادی که روشهای خوشهبندی دارند، استفاده و یا ایجاد تکنیکهایی که در زمان کوتاهتر بتوانند با دقت مناسب پاسخهای خوشهبندی را تولید کنند نیز از موضوعات تحقیقاتی به روز در زمینه یادگیری ماشین بخصوص در فضای کلان دادهها است.
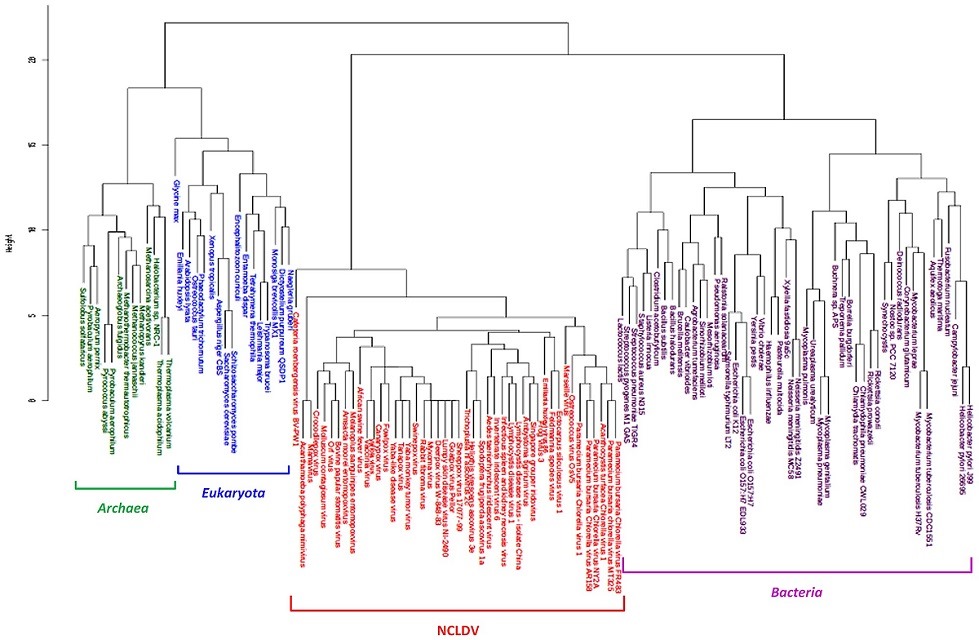
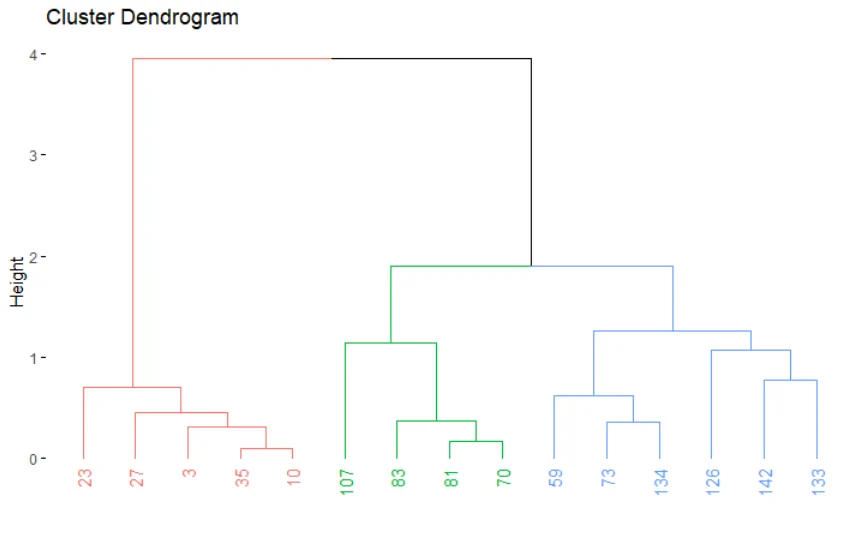
نمودار زیر نتیجه یک خوشهبندی سلسله مراتبی را به صورت «درختواره نگار» (Dendrogram) نشان میدهد.

خوشهبندی سلسله مراتبی با روش تجمیعی: اگر دیدگاه به این نمودار از پایین به بالا باشد (Bottom-Up)، برحسب ارتفاع نمودار (Height) در سطح پایینی، خوشهها زیرمجموعه خوشههای سطح بالاتر هستند در نتیجه به نظر میرسد که خوشههای زیرین با یکدیگر ترکیب شده و خوشههای سطح بالاتر را ایجاد میکنند. این شیوه خوشه بندی سلسله مراتبی به روش «تجمیعی» (Agglomerative) معروف است. برای نامگذاری این روش معمولا از عبارت اختصاری HAC که خلاصه Hierarchical Agglomertive Clustering است، استفاده میشود.
خوشهبندی سلسله مراتبی با روش تقسیمی: برعکس اگر دیدگاه از بالا به پایین (Top-Down) باشد، خوشههای بالایی به زیرخوشهها دیگر تجزیه میشوند تا آنکه به خوشههایی با تنها یک عضو برسیم. به این ترتیب بزرگترین خوشه که شامل همه مشاهدات است به کوچکترین خوشهها که شامل تنها یک مشاهده است تقسیم میشود. به این روش »تقسیمی» (Divisive) گفته میشود. از آنجایی که این روش دارای محدودیتهایی است کمتر در خوشهبندی سلسله مراتبی به کار گرفته میشود. بنابراین در این نوشتار به معرفی روش تجمیعی پرداخته ولی با دستوراتی در R که خوشهبندی تقسیمی را انجام میدهند آشنا میشویم.
پیچیدگی زمانی الگوریتم خوشهبندی سلسله مراتبی تجمیعی
در الگوریتم HAC پیچیدگی زمانی برابر با و فضای مورد نیاز حافظه نیز برابر با است. بنابراین با افزایش حجم دادهها، سرعت و فضای حافظه برای اجرای عملیات خوشهبندی به شدت افزایش مییابد. به همین دلیل معمولا از این الگوریتم برای خوشهبندی «کلان داده» (Big Data) استفاده نمیشود.
مراحل خوشهبندی سلسله تجمیعی
برای اجرای محاسبات مربوط به این روش خوشهبندی، به دو معیار فاصله (شباهت) احتیاج داریم. ۱- میزان فاصله بین زوج مشاهدات. ۲- میزان فاصله بین خوشهها. در حالت اول توابع فاصله برای دادههای کمی یا کیفی قابل استفاده هستند. بنابراین اگر دادهها کمی باشند برای مثال میتوان از فاصله اقلیدسی یا فاصله منهتن استفاده کرد. همچنین برای دادههای کیفی نیز میتوان از میزان انطباق ساده (Simple Matching) و یا «فاصله همینگ» (Hamming Distance) برای داده های کمک گرفت.
معمولا قبل از شروع مراحل خوشهبندی سلسله مراتبی تجمیعی، از یک «ماتریس فاصله» (Distance Matrix) یا «ماتریس شباهت» (Similarity Matrix) برای تسریع در محاسبات کمک گرفته میشود. این ماتریس نشان میدهد که فاصله بین هر زوج از مشاهدات چقدر است. البته نوع تابعی که باید بوسیله آن فاصله اندازهگیری شود، در مقدارهای موجود در این ماتریس تاثیر گذار است.
در خوشهبندی سلسله مراتبی تجمیعی یا HAC، با توجه به مقدارهای این ماتریس، مشاهدات یا خوشههایی که دارای کمترین فاصله (بیشترین شباهت) هستند با هم ادغام میشوند و خوشه جدیدی میسازند. در مرحله بعد باز هم فاصله بین مشاهدات و یا خوشههای جدید، توسط ماتریس فاصله که به روز رسانی شده، محاسبه و کار ادغام ادامه پیدا میکند تا تنها یک خوشه باقی بماند.
توابع اندازهگیری فاصله بین مشاهدات
در جدول زیر به معرفی شیوه محاسبه فاصله بین مشاهدات برای دادههای کمی پرداخته شده است:
| نام تابع | شیوه محاسبه |
| فاصله اقلیدسی (Euclidean Distance) | |
| مربع فاصله اقلیدسی (Squared Euclidean Distance) | |
| فاصله منهتن (Manhattan Distance) | |
| فاصله حداکثر (Maximum Distance) | |
| فاصله ماهالانویس (Mahalanobis) در اینجا S ماتریس کواریانس و T نیز به معنی ترانهاده ماتریس است. |
در مقام مقایسه بین این توابع فاصله، میتوان دید که فاصله اقلیدسی بیشتر در مطالعات مربوط به روانشناسی، علوم کامپیوتر و کسب و کار تجاری به کار گرفته شده است. در زیر یک نمونه از ماتریس فاصله را برای دادههای یک بعدی با مقدارهای براساس فاصله اقلیدسی مشاهده میکنید.
همانطور که دیده میشود، عناصر روی قطر اصلی این ماتریس برابر با صفر هستند زیرا فاصله هر مشاهده از خودش برابر با صفر است. همچنین این ماتریس متقارن است به این معنی که برای مثال فاصله مشاهده اول با دوم برابر با فاصله مشاهده دوم از اول است.
البته باید توجه داشت که استفاده از فاصله بین زوج مشاهدات در بیشتر روشهای خوشهبندی استفاده میشود. ولی نکتهای که خوشهبندی سلسله مراتبی را نسبت به بقیه روشها مجزا میکند، سنجش فاصله بین خوشههای است. به این ترتیب دو خوشهای که بیشترین شباهت (کمترین فاصله) با یکدیگر را داشته باشند با هم ادغام شده و خوشه جدیدی میسازند. پس در هر مرحله فقط امکان ترکیب دو خوشه وجود دارد. این مراحل را به نام «سطوح ادغام» (Merge Level) میشناسیم.
در ادامه به بررسی روشهای اندازهگیری فاصله بین خوشهها میپردازیم که البته به بهترین وجه در خوشه بندی سلسله مراتبی به کار گرفته میشود.
اندازهگیری فاصله بین خوشهها یا روشهای پیوند (Linkage Methods)
معیارهای مختلفی برای اندازهگیری فاصله بین خوشهها میتوان به کار برد. برای مثال میتوان فاصله را براساس فاصله بین نزدیکترین یا دورترین مشاهدات بین دو خوشه در نظر گرفت. هر یک از این معیارها معایب و مزایای مخصوص به خود را دارند. ولی با توجه به ساختار دادهها (وجود دادههای پرت، الگوی قرارگیری (پراکندگی) مشاهدات در هر خوشه و... میتوان مبنای انتخاب یکی از روشهای پیوند باشد.
جدول زیر به معرفی روشهای پیوند و شیوه محاسبه هر یک پرداخته است. در این فرض شده است که باید فاصله بین دو خوشه A و B اندازهگیری شود. در ضمن d نیز تابع فاصله دلخواه است که میتواند از جدول بالا انتخاب شود.
| نام روش پیوند | شیوه محاسبه |
| دورترین فاصله یا پیوند کامل (Complete-Linkage) | |
| نزدیکترین فاصله یا پیوند تکی (Single-Linkage) | |
| پیوند میانگین - UPGMA
(Unweighted Pair Group Method with Arithmetic Mean) | |
| پیوند مرکزی یا فاصله بین نقاط مرکزی هر خوشه - UPGMC
(Unweighted Pair Group Method with Arithmetic Mea) | |
| روش Ward | محاسبه براساس تابع هدف و کمینه سازی واریانس خوشههای ترکیبی |
نکته: اهمیت روشهای پیوند کامل و تکی در این است که میتوان برای محاسبه فاصله بین خوشهها فقط از ماتریس فاصله استفاده کرد و دیگر به مشاهدات نیازی نیست.
اجرای خوشهبندی سلسله مراتبی با R
در این قسمت به بررسی و معرفی توابع در R میپردازیم که عملیات خوشهبندی سلسله مراتبی را انجام میدهند. همانطور که قبلا اشاره کردیم، ابتدا باید ماتریس فاصله تعیین شده سپس مراحل خوشهبندی طی شود.
کدهای بالا به منظور ایجاد سه خوشه (k=3) برای یک نمونه ۱۵ تایی از دادههای iris نوشته شده است. میدانیم در این دادههای سه دسته گل وجود دارد، به همین علت به طور تصادفی از هر دسته ۵۰ تایی یک نمونه ۵ تایی (n=5) تهیه شده تا مشاهده نمودار و خروجیهای خوشهبندی سلسله مراتبی بهتر دیده شود.
تابعی که برای اندازهگیری فاصله بین مشاهدات و یا خوشهها در نظر گرفته شده، فاصله اقلیدسی است. از طرف دیگر، معیار پیوند خوشههای نیز پیوند میانگین (average) منظور شده و محاسبات براساس آن صورت گرفته است. ماتریس فاصله که توسط دستور dist تولید شده در متغیر distance و خروجی دستور hclust که عملیات خوشهبندی سلسله مراتبی را صورت میدهد، در متغیر hc قرار دارد.
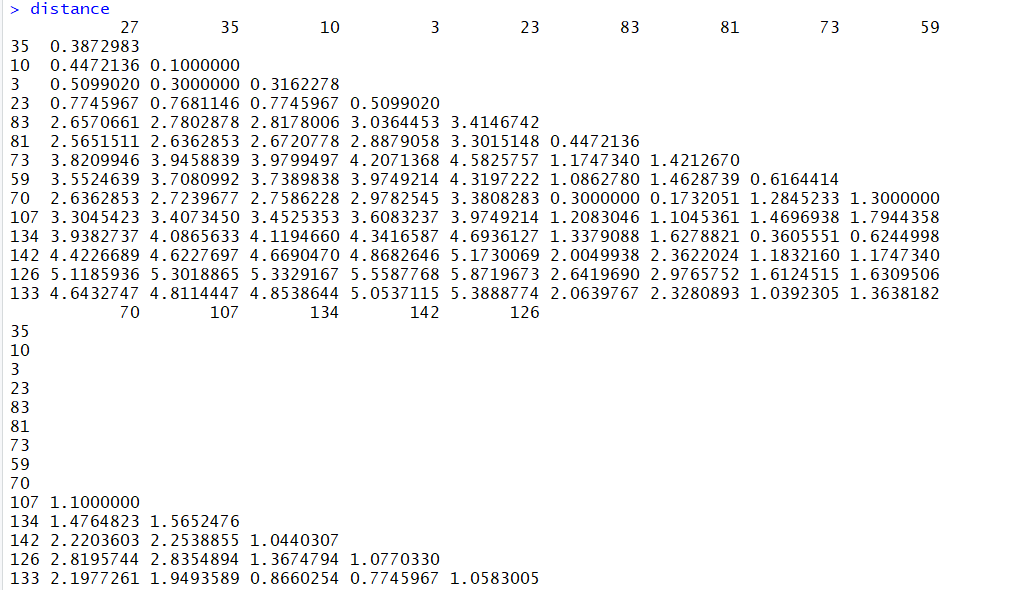
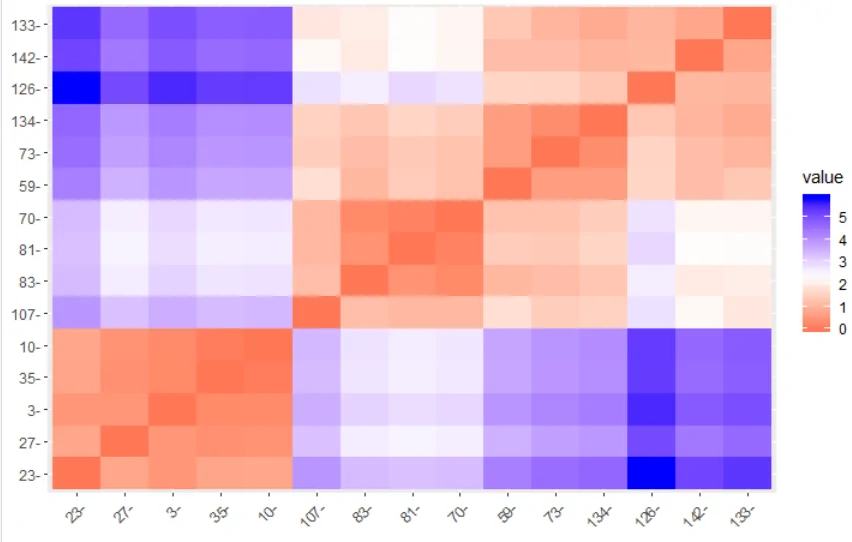
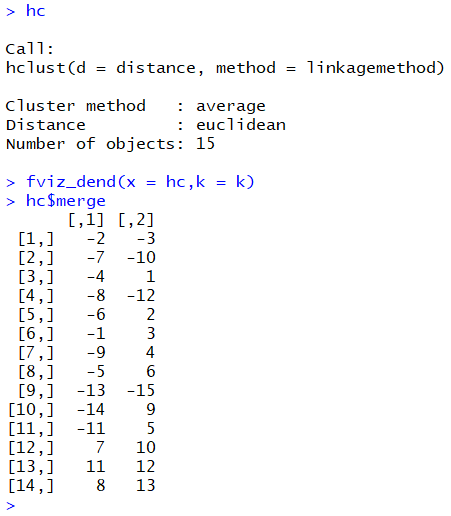
با استفاده از بسته factoextra امکان نمایش ماتریس فاصله و درختواره نگار به زیبایی وجود دارد. دستورات fviz_dist ماتریس فاصله را به صورت تصویری و fviz_dend درختواره نگار را نمایش میدهد.
در انتها نیز با اجرای دستور hc$merge مراحل ادغام خوشهها دیده میشود. مقدارهای منفی شماره مشاهده و مقدارهای مثبت در این لیست نشاندهنده شماره خوشهای است که در مرحلههای قبلی ایجاد شده و در این مرحله عمل ادغام رویشان صورت گرفته است. در تصویر زیر درختواره نگار مربوط به این دادههای نمایش داده شده است. از آنجایی که تعداد خوشههای مورد نظر را ۳ وارد کردهایم، نمودار به سه رنگ مختلف، اعضای هر خوشه را متمایز کرده.
نکته: توجه داشته باشید که با اجرای مجدد این کدها ممکن است خروجیها تغییر کند زیرا محاسبات براساس نمونههای تصادفی از اطلاعات اصلی حاصل شده. اگر میخواهید همیشه نتایج یکسانی از این برنامه دریافت کنید بهتر است خط را در ابتدای برنامه وارد کنید.
اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزشهایی که در ادامه آمدهاند نیز برایتان کاربردی خواهند بود.
- مجموعه آموزشهای یادگیری ماشین و بازشناسی الگو
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS
- آموزش خوشه بندی تفکیکی با نرم افزار R
- آموزش خوشه بندی سلسله مراتبی با SPSS
- آشنایی با خوشهبندی (Clustering) و شیوههای مختلف آن
- روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای درونی (Internal Index)
- روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای بیرونی (External Index)
^^













سلام وقت شما بخیر..
ممنون از اطلاعات مفیدتون.
سوالم این هست که اگر ما یه مجموعه داده داشته باشیم و بخواییم با یک نوع از الگوریتم های سلسله مراتبی خوشه بندی کنیم، چه تفاوتی دارد که از روش بالا به پایین استفاده کنیم یا روش پایین به بالا؟ ینی روش تجمیعی یا روش تقسیمی چه مزیتی نسبت به هم دارند؟ و کدوم عملکرد بهتری دارند؟
ممنون میشم توضيح بفرمایید..
با تشکر.